Canonical Metrics on Generalized Cartan-Hartogs Domains∗

Yihong HAO

1 Introduction

In order to find the canonical representant of a given Ka¨hler class[ω]of a complex compact K¨ahler manifold(M,J),Calabi made a search in[3–4].He introduced the notion of the extremal metric defined as the minimizer of the L2-norm of the Ricci tensor.This notion is one of the generalizations of the K¨ahler-Einstein metric.Let sgbe the scalar curvature of the K¨ahler metric g.He proved that g is an extremal metric if and only if∇sgis a holomorphic vector field.From the Euler-Lagrange equation for sg,the metrics with constant scalar curvatures,in particular the K¨ahler-Einstein metrics,are extremal.He also proved that some extremal metrics with non-constant scalar curvatures do exist.

The existence and uniqueness of the extremal metrics in some given K¨ahler classes have been studied(see[7,13,18]).The important relationship between the existence of extremal metrics and various stability notions of the corresponding polarized manifolds has also been deeply investigated(see[2,11–12,19–22,24]).However,a complete understanding of the existence theory for extremal metrics is still missing.One can see some recent progress on the study of Calabi’s extremal K¨ahler metrics in[23].

In general,the problem of finding extremal metrics is quite natural but difficult(see[27]).On a complete noncompact smooth surface,Chang[6]proved the existence of extremal metrics.On a strongly pseudoconvex Hartogs domain,Loi and Zedda[16]proved that the only extremal metric is the hyperbolic metric.On Cartan-Hartogs domains endowed with their natural K¨ahler metrics,Zedda[29]proved that they are extremal if and only if they are K¨ahler-Einstein.In this paper,we extend Zedda’s result to(Ω(μ,m),gΩ(μ,m)),i.e.,the generalized Cartan-Hartogs domain endowed with a natural K¨ahler metric gΩ(μ,m),where all elements of the vector μ ∈ Rmare positive(see the definition in Section 3).This domain is a Hartogs domain over the product of irreducible bounded symmetric domains.In particular,Ω(μ,1)is exactly the Cartan-Hartogs domain introduced by Yin,Roos[26].The first result of the paper is the following two theorems.

Theorem 1.1 Let Ω(μ,m)⊂ Cnbe the generalized Cartan-Hartogs domain given by(3.1).Then the K¨ahler metric gΩ(μ,m)in(3.2)is extremal if and only if its scalar curvature is a constant,i.e.,μ =(μ1,μ2,···,μm)satisfies the equation

Theorem 1.2 The metric gΩ(μ,m)in(3.2)is K¨ahler-Einstein if and only if the parameter

As we know,the Bergman metric,the K ¨ahler-Einstein metric,the Carath´eodary metric,and the Koboyashi metric are four classical invariant metrics.It is interesting to study the comparison theorem among them.For the holomorphic homogeneous regular manifolds(also called the uniformly squeezing domains)introduced by Liu,Sun,Yau and Yeung independently,the four classical invariant metrics on a homogenous regular domain are equivalent(see[15,28]).It is known that bounded homogeneous domains,bounded strongly convex domains,bounded domains which cover a compact K¨ahler manifold,TeichmÜller spaces Tg,nof hyperbolic Riemann surfaces of genus g with n punctures,strongly pseudoconvex domains with C2boundary,Cartan-Hartogs domains,and bounded convex domains are such domains(see[10,14–15,28]).In this paper,we prove that Ω(μ,m)is also holomorphic homogeneous regular(with the uniform squeezing property).This implies our second result Theorem 4.2.

This paper is organized as follows.We start by recalling some notions and results for Cartan domains and holomorphic homogeneous regular domains(uniformly squeezing domains)in Section 2.By investigating the geometry of(Ω(μ,m),gΩ(μ,m)),we obtain Theorems 1.1–1.2 in Section 3.Finally,we prove that Ω(μ,m)is a holomorphic homogeneous regular domain in Section 4,which implies that the four classical metrics are equivalent.

2 Preliminaries

2.1 Cartan domains

In this section,we recall some results of the irreducible bounded symmetric domains which have been completely classified up to a biholomorphic isomorphism due to Cartan[5].

Let Mm,nbe the space of m×n complex matrices,I be the identity matrix,z be the conjugate matrix of z,and ztbe the transposed matrix of z.If a square matrix A is positive definite,then we denote it by A>0.The list of irreducible bounded symmetric domains and the corresponding generic norms is the following(see[17,Chapter 4]):

HereOC=C⊗O is complex 8 dimensional Cayley algebra.M3,3(OC)is the space of 3×3 matrices with entries in the spaceOCof octonions over C,which are Hermitian with respect to the Cayley conjugation.z?is the adjoint matrix inM3,3(OC),(z|ζ)is the standard Hermitian product inM3,3(OC),andM2,1(OC)is a subspace ofM3,3(OC).

The domains of types I–IV are classical,whileDVandDVIare the exceptional 16 and 27 dimensional domains.These domains are also called Cartan domains(also see the details in[1,Section 2]).The genusγ,the rankr,and the numerical invariantsaandbfor an irreducible bounded symmetric domainDhave the following relation:

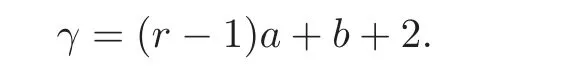
The parameters of those domains are given in Table 1.

Table 1 Parameters of Cartan domains

The connection between the generic normN(z,z)and the Bergman kernelK(z,z)of the bounded symmetric domainDis

whereV(D)is the volume ofD.LetgDbe the Bergman metric,and then

(see(13)in[25]).

In the following,we study the derivative of the generic norm at zero.Letz=(z1,z2,···,zd)be the coordinate of the Cartan domainD⊂Cd.Since the Cartan domain is a circular domain with its center at 0,we have

It turns out that

for 1≤α,β≤d.Since the Bergman metric

noticing that gD|z=0=γI(d)(see[17]),we have

where I(d)is the d×d identity matrix.and then

It follows that the real Hessian of the general norm N at the origin is

2.2 Squeezing function

The notion of the squeezing function introduced by Deng,Guan,and Zhang is useful for studying the geometric and analytic properties of bounded domains(see[9]).In this section,we will recall some properties of the squeezing function which will be used in Section 4.

Definition 2.1(see[9])Let D be a bounded domain in Cn.For z∈D and an(open)holomorphic embedding f:D→Bnwith f(z)=0,define

and the squeezing number sD(z)of D at z is defined as

where the supremum is taken over all holomorphic embeddings f:D→Bnwith f(z)=0,Bnis the unit ball in Cn,and Bn(0,r)is the ball in Cnwith center 0 and radius r.The function sDis called the squeezing function of D.

The definition shows that the holomorphic homogenous regular domain is a bounded domain whose squeezing function is bounded below by a positive constant and the squeezing function is invariant under the biholomorphic transformation.From[9],we know that the squeezing function is continuous.Hence,the boundary behavior of a squeezing function is important for studying its boundedness.

Definition 2.2(see[10])A point p is called a globally strongly convex boundary point of D if∂D is C2smooth and strongly convex at p,and D∩Tp∂D=p,where Tp∂D is the tangent hyperplane of∂D at p.

Theorem 2.1(see[10])Let D⊂Cnbe a bounded domain.Assume that p∈∂D is a globally strongly convex boundary point of D.Then

By this theorem,if the boundedness of the squeezing function of a bounded domain depends on its globally strongly convex boundary points,then we know that it is a holomorphic homogeneous regular domain immediately,for example,bounded strongly pseudoconvex domains with C2smooth boundaries and Cartan-Hartogs domains.In Section 4,we will show that the generalized Cartan-Hartogs domain has the similar property.

3 The Geometry of(Ω(µ,m),gΩ(µ,m))

Let D×?=D1×D2×···×Dm×?be the product of finite Cartan domains Di⊂ Cdiand the disc? ⊂ C.The coordinates of Diand?are denoted by zi=(zi1,zi2,···,zidi)in Cdiand ξ in C respectively.and write(z,ξ):=(z1,z2,···,zm,ξ)∈ Cd1× ···×Cdm×C.The generalized Cartan-Hartogs domain Ω(μ,m)associated to D is defined to be

where m is a positive integer,μ is an m-vector with the positive real numbers μias its i-element and Ni(zi,wi)is the generic norm of Diwith the dimension n=d+1.

In[25],Wang and Hao have computed the explicit form of the uniquely complete K¨ahler-Einstein metric in the case thatThe Khler potential is

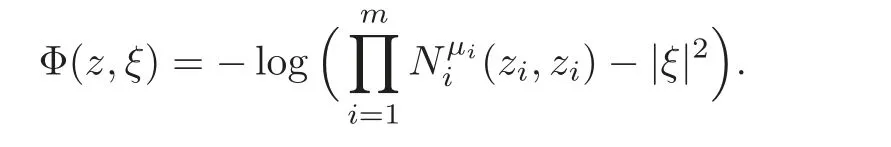
In this section,we consider the domain Ω(μ,m)equipped with a natural K¨ahler metric gΩ(μ,m),i.e.,in the neighbourhood of the origin,the K¨ahler form associated to gΩ(μ,m)is

where the Khler potential

By(2.1),we know Φ is a C∞strictly plurisubharmonic function on Ω(μ,m).So gΩ(μ,m)is a Khler metric.Actually,it is just the natural complete K¨ahler metric given by a defining function of the domain.This K¨ahler metric was constructed by Cheng and Yau on the strictly pseudoconvex domain with Ck,k≥5 boundary in Cnfirstly(see[8]).Now,we will describe the case when(Ω(μ,m),gΩ(μ,m))is a complete extremal K¨ahler manifold.

Let gΩ(μ,m)also denote its metric matrix,i.e.,

where

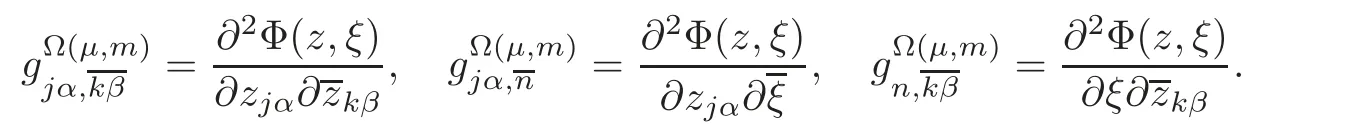
Lemma 3.1 The metric gΩ(μ,m)satisfies the following equation:

where

Proof For convenient,we define

for 1≤j,k≤m.By a straightforward computation,the metric

where the upper left block is a d×d submatrix.Under the elementary transformations,the matrix can be transformed into

and

It implies that the upper left block of(3.6)is a block diagonal matrix.

Let gDibe the Bergman metric of Di,andbe the(α,β)-entry ofThen

Hence,we have

From(2.2)and the equation above,it follows that

We complete the proof.

By using the standard formula of Ricci tensor,we can obtain the following lemma directly.

Lemma 3.2 The Ricci tensor of gΩ(μ,m)is

Corollary 3.1 gΩ(μ,m)is K¨ahler-Einstein if and only if μi=for 1≤i≤m.

Let

be the inverse matrix of gΩ(μ,m),where 1≤ j,k≤ m and 1≤ α ≤ dj,1≤ β ≤ dk.Letbe the inverse matrix of the Bergman metric matrix

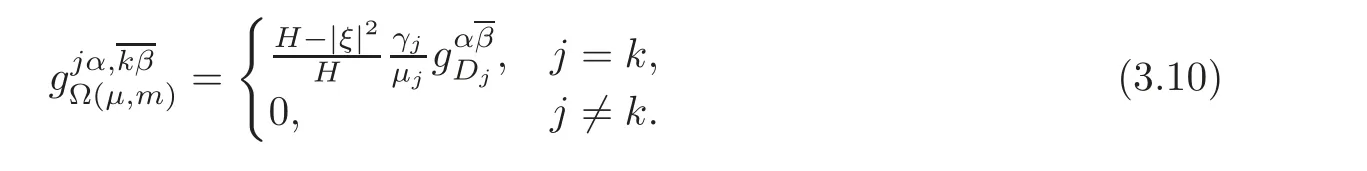
This equation shows that the upper left block of(3.9)is a block diagonal matrix.

Let sgbe the scalar curvature of gΩ(μ,m),and we have

Lemma 3.3 The scalar curvature of gΩ(μ,m)is

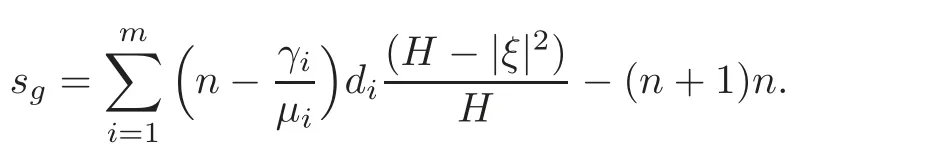
Corollary 3.2 sgis a constant if and only

Now we study the extremal condition.Let(M,g)be an n-dimensional K¨ahler manifold,and(z1,···,zn)be the local coordinate in a neighborhood of p ∈ M.From[3],the extremal condition can be given by the following equation:

for all α,η =1,···,n.By using(3.11),we can obtain our main result in this section.

Theorem 3.1 The metric gΩ(μ,m)is extremal if and only if its scalar curvature sgis a constant,i.e.,

Proof.By Calabi’s result,we only need to prove that gΩ(μ,m)is not an extremal metric if τ?=0.By Lemma 3.3,

Let A=gΩ(μ,m)andbe the algebraic cofactor oLet B be the upper left d × d block matrix of A,i.e.,

In our case,the extremal condition(3.11)turns out to be

Thus we know that gΩ(μ,m)is not extremal if τ?0.

Remark 3.1 In particular,Ω(μ,1)is the Cartan-Hartogsdomain over an irreducible bounded symmetric domain D.We can obtain Loi and Zedda’s results in[29].Their results can be summarized as follows.Let γ be the genus of D and n be the total dimension of Ω(μ,1).Then

(1)gΩ(μ,1)is an extremal metric;

(2)gΩ(μ,1)is a K¨ahler-Einstein metric;

(3)the scalar curvature of gΩ(μ,1)is a constant;

(4)the parameter μ equalsare equivalent.

4 The Equivalence of Four Classical Metrics

In[10],Deng,Guan and Zhang proved that Cartan-Hartogs domains are holomorphic homogeneous regular domains(i.e.,they have the uniform squeezing property).As a generalization,we will show that their method is also valid for the generalized Cartan-Hartogs domain defined in(3.1).

In the following,we investigate the boundary ∂(Ω(μ,m))of Ω(μ,m).By(3.1),it is easy to see that

where ∂D × {0}={(z,0):z ∈ ∂D}and ∂0(Ω(μ,m))={(z,ξ)∈ D × C:ρ(z,ξ)=0,ξ0}.Now we claim that ρ is a local defining function of Ω(μ,m)at the boundary pointIn fact,let V()⊂D be a neighborhood ofand?(,r)be a disc with radius r<.Then the neighborhood U()=V()×?(,r)ofsatisfies and dρ(z,ξ)?0 for(z,ξ)∈ U().So the claim is true.Moveover,ρ is smooth by(2.1).

In[25],we have constructed a holomorphic automorphism subgroup G of Aut(Ω(μ,m)).The domain Ω(μ,m)has the following characteristic:For any fixed point p=(z,ξ)∈ Ω(μ,m),there always exists Ψ ∈ G such that Ψ(z,ξ)=(0,ξ∗)for some real number ξ∗∈ [0,1).Let G act on Ω(μ,m)through the action G×Ω(μ,m)→ Ω(μ,m).The orbit of a point p ∈ Ω(μ,m)is Op={Ψ(p)∈ Ω(μ,m):Ψ ∈ G}.Thus the set of all the orbits can be written in the followingBy the holomorphic invariant property of the squeezing function,we have

for(z,ξ)∈ Ω(μ,m).

Theorem 4.1 Ω(μ,m)is a holomorphic homogeneous regular domain.

Proof We have proved that ρ is a local defining function of the boundary of Ω(μ,m)at the boundary point(0,1)∈ ∂0(Ω(μ,m)).In view of(2.7),the real Hessian

where the upper left block is a 2d×2d submatrix.Let ξ=u+iv.Note thatand then the tangent hyperplane T(0,1)∂(Ω(μ,m))={u=1}.It is clear that Ω(μ,m)∩ {u=1}={(0,1)},so(0,1)is a globally strongly convex boundary point of Ω(μ,m).By TheoremFurthermore,s(x)=sΩ(0,x)is continuous in[0,1].By(4.2),sΩis bounded blow by a positive number and Ω(μ,m)is a holomorphic homogeneous regular domain.

From[15,28],we know that homogeneous regular domains have many interesting properties.One of the properties is the equivalence of four classical metrics.So we have the following result.

Theorem 4.2 The Bergman metric,the K¨ahler-Einstein metric,the Carath´eodary metric,and the Koboyashi metric on Ω(μ,m)are equivalent.

[1]Arazy,J.,A survey of invariant Hilbert spaces of analytic functions on bounded symmetric domains,Contemp.Math.,185,1995,7–65.

[2]Berman,R.J.,K-polystability of Q-Fano varieties admitting K¨ahler–Einstein metrics,2012.arXiv:1205.6214

[3]Calabi,E.,Extremal K¨ahler metrics,Seminar on differential Geometry,Ann.of Math.Stud.,Vol.102,Princeton Univ.Press,Princeton,N.J.,1982,259–290.

[4]Calabi,E.,Extremal K¨ahler Metrics II,Differential Geometry and Complex Analysis,Springer-Verlag,Berlin Heidelberg,1985,95–114.

[5]Cartan,E.,Surles domaines born`es homogenes de l’espace de n variables complexes,Abh.Math.Sem.Univ.Hamburg,11(1),1935,116–162.

[6]Chang,S.C.,On the existence of nontrivial extremal metrics on complete noncompact surfaces,Math.Ann.,324(3),2002,465–490.

[7]Chen,X.and Tian,G.,Uniqueness of extremal K¨ahler metrics,C.R.Math.Acad.Sci.Paris,Ser.,340(4),2005,287–290.

[8]Cheng,S.Y.and Yau,S.T.,On the existence of a complete K¨ahler metric on non-compact complex manifolds and the regularity of Fefferman’s equation,Comm.Pure Appl.Math.,33(4),1980,507–544.

[9]Deng,F.,Guan,Q.and Zhang,L.,Some properties of squeezing functions on bounded domains,Pacific J.Math.,257(2),2012,319–341.

[10]Deng,F.,Guan,Q.and Zhang,L.,Properties of squeezing functions and global transformations of bounded domains,2013.arXiv:1302.5307

[11]Donaldson,S.K.,Scalar curvature and projective embeddings,I,J.Differential Geom.,59(3),2001,479–522.

[12]Donaldson,S.K.,Lower bounds on the Calabi functional,J.Differential Geom.,70(3),2005,453–472.

[13]Guan,D.,Existence of extremal metrics on compact almost homogeneous K¨ahler manifolds with two ends,Trans.Amer.Math.Soc.,347(6),1995,2255–2262.

[14]Kim,K.T.and Zhang,L.,On the uniform squeezing property and the squeezing function,2013.arXiv:1306.2390

[15]Liu,K.,Sun,X.and Yau,S.T.,Canonical metrics on the moduli space of Riemann surfaces I,J.Differential Geom.,68(3),2004,571–637.

[16]Loi,A.and Zuddas,F.,Canonical metrics on Hartogs domains,Osaka J.Math.,47(2),2010,507–521.

[17]Loos,O.,Bounded symmetric domains and Jordan pairs,University of California,1977.

[18]Mabuchi,T.,Uniqueness of extremal K¨ahler metrics for an integral K¨ahler class,Intern.J.Math.,15(6),2004,531–546.

[19]Mabuchi,T.,K-stability of constant scalar curvature polarization,2008.arXiv:0812.4093

[20]Paul,S.T.,Hyperdiscriminant polytopes,Chow polytopes,and Mabuchi energy asymptotics,Ann.of Math.,175(1),2012,255–296.

[21]Stoppa,J.,K-stability of constant scalar curvature K¨ahler manifolds,Adv.Math.,221(4),2009,1397–1408.[22]Stoppa,J.and Sz´ekelyhidi G.,Relative K-stability of extremal metrics,J.Eur.Math.Soc.,13(4),2011,899–909.

[23]Sz´ekelyhidi,G.,Extremal metrics and K-stability,E Bull.Lond.Math.Soc.,39,2007,76–84

[24]Tian,G.,K¨ahler-Einstein metrics with positive scalar curvature,Invent.Math.,130(1),1997,1–37.

[25]Wang,A.and Hao,Y.,The explicit solutions for a class of complex Monge-Ampere equations,Nonlinear Anal.Theor.,95,2014,639–649.

[26]Wang,A.,Yin,W.,Zhang,L.and Roos,G.,The K¨ahler-Einstein metric for some Hartogs domains over symmetric domains,Sci.Chin.Ser.A:Math.,49(9),2006,1175–1210.

[27]Xu,X.W.,On the existence of extremal metrics,Pacific J.Math.,174,1996,555–568.

[28]Yeung,S.K.,Geometry of domains with the uniform squeezing property,Adv.Math.,221(2),2009,547–569.

[29]Zedda,M.,Canonical metrics on Cartan-Hartogs domains,Int.J.Geom.Methods M.,9(1),2012,1250011,13 pages.