地表曲率变形对房屋墙体损坏的数值模拟研究
2016-06-08廉旭刚陈胜云胡海峰
廉旭刚,陈胜云,胡海峰
(太原理工大学 测绘科学与技术系,山西 太原 030024)
地表曲率变形对房屋墙体损坏的数值模拟研究
廉旭刚,陈胜云,胡海峰
(太原理工大学 测绘科学与技术系,山西 太原 030024)
[摘要]为了研究地下煤层开采造成的地表曲率变形对地面建筑物破坏影响,应用有限元软件Comsol Multiphysics构建了单面墙体受地面曲率影响的模型,分别从正、负曲率两个方面模拟分析了地表破坏Ⅰ~Ⅳ级时地面的曲率情况,得到了在不同工况条件下,墙体应力的变化规律。当墙体受正曲率影响时,上部受到拉应力作用,墙体易形成倒“八”字裂缝,且随曲率增大,上部拉应力增大;当墙体受负曲率影响时,下部受到拉应力,墙体易形成正“八”字裂缝,且随曲率增大,下部拉应力增大。通过现场实例分析,验证了房屋墙体裂缝形态与地表曲率的关系,为建筑物下采煤的安全防护提供了技术支持。
[关键词]曲率变形;墙体变形;开采沉陷;有限元模拟
Numerical Simulation of Wall Damage by Surface Curvature Deformation
地下煤层开采造成了上覆岩层及地表移动变形,引起地表建构筑物的变形与破坏。开采沉陷造成地表移动变形的指标有下沉、倾斜、曲率、水平移动、水平变形等。其中曲率对建筑物的影响较大。目前国内外许多学者对采动变形作用下建筑物基础和地基相互作用进行了实测和理论方面研究工作,并取得了一些成果。
题正义以概率积分法为基础,计算地表移动变形岩移参数,根据计算得出的地表水平移动值和最大正、负曲率值来判定地表建筑物损害程度,分析主断面上的移动变形,确定了移动盆地主断面位置[1]。冯宝红分析了建构筑物破坏现象产生的机理及其影响规律,得出建筑物产生破坏和变形的主要原因是曲率和水平变形的影响,在其作用下,采动区地面建筑物砖墙上出现裂缝[2]。梁为民考虑了建筑物横墙荷载对纵墙基础的作用,提出建筑物纵墙地基反力的计算模型,推导出纵墙基础受到曲率变形影响下的附加作用力计算公式[3]。刘书贤探讨重复强开采条件下地表移动诱发建筑物裂缝的成因机制,高频次高强度的重复开采活动削弱了煤柱稳定性,导致采空区上覆岩层移动变形破坏加剧,增大了原有的地表下沉趋势[4]。郭麒麟基于随机介质理论推导了开采影响下单个剖面上的岩体内部的移动和变形计算公式,探讨了水平剖面及倾斜剖面上留设煤柱的影响,并对双向非充分开采时岩土体的移动和变形计算作了一定的研究[5]。冯军基于建筑物临界变形值原则,提出了采用宽条带跳采开采技术来提高煤炭的采出率,解放深部建筑物下的压煤,并利用FLAC进行数值模拟,分析了跳采开采和顺序开采对地表的影响[7]。赵飞采用离散元数值模拟方法对青山煤矿同一水平急倾斜煤层群开采后地表沉陷规律、煤层顶底板在重复采动条件下的移动规律进行了研究,分析了地表易产生非连续变形和突发性破坏的机理[8]。王刚根据地下开采地表移动规律,借鉴建筑物下、水体下、铁路下采煤,结合高等级公路自身的特点,分别讨论了地下开采引起的地表下沉、倾斜、曲率、水平移动和水平变形对高等级公路的破坏机理[9]。朱庆伟采用FLAC3D对大采高浅埋深土层条件下的地表桥梁建筑物进行开采沉陷预计分析,初步确定了沉陷影响的范围,结果表明:地表局部下沉后引起的倾斜是造成桥梁建筑物破坏的主要因素之一[10]。姚文华利用概率积分法定量研究了地表受采动影响在时间和空间上的变化规律。为工作面上方建筑物的搬迁、赔偿、以及建筑物损害等级的评定提供了依据[11]。
为研究曲率对房屋的影响,本文假设房屋的跨度相对于下沉盆地较小,可用房屋两端的曲率平均值代表房屋受到的曲率影响。房屋在下沉盆地的不同位置受到正负不同的曲率影响,如图1所示。
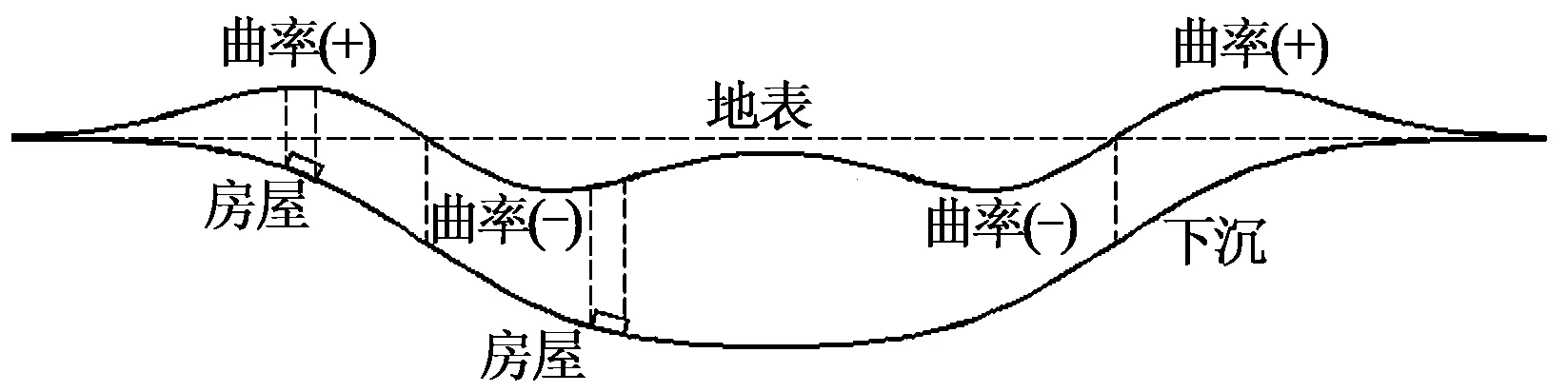
图1 曲率变形与下沉关系示意
1地表曲率影响下墙体计算模型
模型建立的背景:在地表发生正曲率变形时,地表由原来的形态变为“凸”型地貌;地表发生负曲率变形时,地表呈现“凹”型地貌。模型建立的假设:认为建筑物下方地表形态发生变化后,可根据发生变形的情况,近似的模拟为“采空区”。因此,可以根据地表因曲率变形而产生的采空区大小来模拟墙体受到破坏后的应力变化。
COMSOL Multiphysics模拟软件是以有限元法为基础,通过求解偏微分方程(单场)或偏微分方程组(多场)来实现真实物理现象的仿真。以单面墙体为研究对象,按照砖混结构建构筑破坏Ⅰ~Ⅳ级,分别建立4种模型:墙体受到Ⅰ级破坏时,地表的曲率变形为0.2mm/m2,曲率半径R1=5000m;受到Ⅱ级破坏时,地表的曲率变形为0.4mm/m2,曲率半径R2=2500m;受到Ⅲ级破坏时,地表的曲率变形为0.6mm/m2,曲率半径R3=1600m;受到Ⅳ级破坏时,地表的曲率变形大于0.6mm/m2,本次模拟取0.8mm/m2,曲率半径R4=1250m。
为了建立曲率半径与模拟“采空区”之间的关系,图2建立了地表正曲率时采空区尺寸模型。在计算地表正曲率采空区尺寸时,lab=lde=lcf=R(1-cosθ),由于R≫lbf,所以θ角为微小角,故θ可取值为θ=sinθ=(r+L/2)/R,由于θ角为微小角,故cosθ=1-θ2/2,则
lab=lde=lcf=Rθ2/2=(r+L/2)2/2R
(1)
式中,lab,lde为采空区最大垂向高度,m;R为曲率半径,m;r为地基曲率主要影响半径,m;L为墙体水平长度,m。
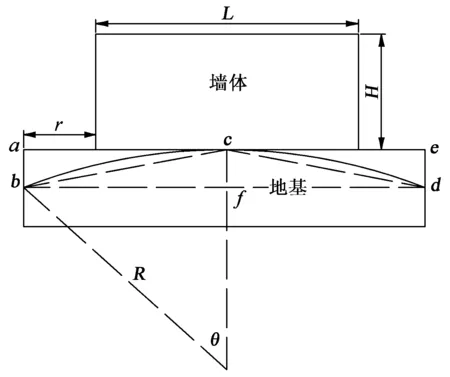
图2 地表正曲率时采空区尺寸模型
图3为某一特定尺寸下,根据以上模型建立的正曲率影响时不同等级曲率半径与采空区尺寸之间的关系。按照公式(1),4种破坏等级的曲率、曲率半径与模拟采空区最大垂向高度之间的对应关系为:Ⅰ级破坏-曲率0.2mm/m2-曲率半径R1=5000m-采空区最大垂向高度l1=0.245m;Ⅱ级破坏-曲率0.4mm/m2-曲率半径R2=2500m-采空区最大垂向高度l2=0.49m;Ⅲ级破坏-曲率0.6mm/m2-曲率半径R3=1600m-采空区最大垂向高度l3=0.77m;Ⅳ级破坏-曲率0.8mm/m2-曲率半径R4=1250m-采空区最大垂向高度l4=0.98m。
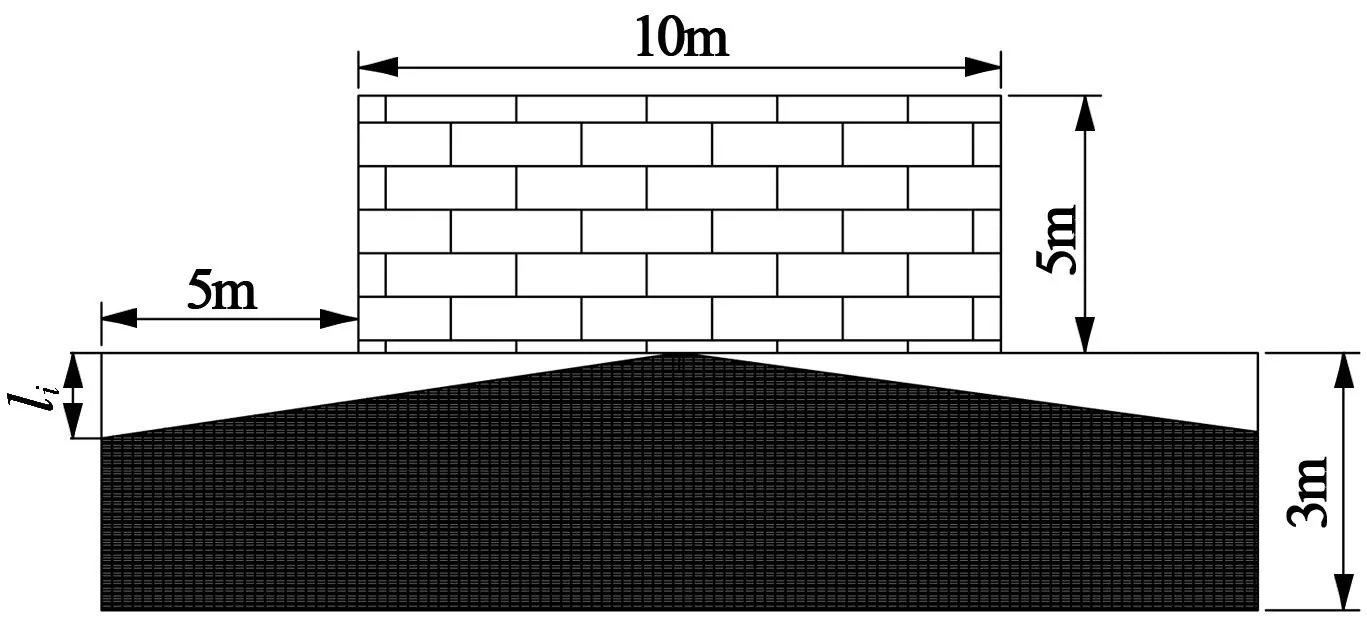
图3 地表正曲率墙体变形有限元模型
同理,建立负曲率影响时,曲率半径与采空区尺寸之间的关系模型见图4。可得
ldc=R(1-cosθ′)=Rθ′2/2=L2/8R
(2)
式中,ldc为采空区最大垂向高度,m;R为曲率半径,m;L为墙体水平长度,m。
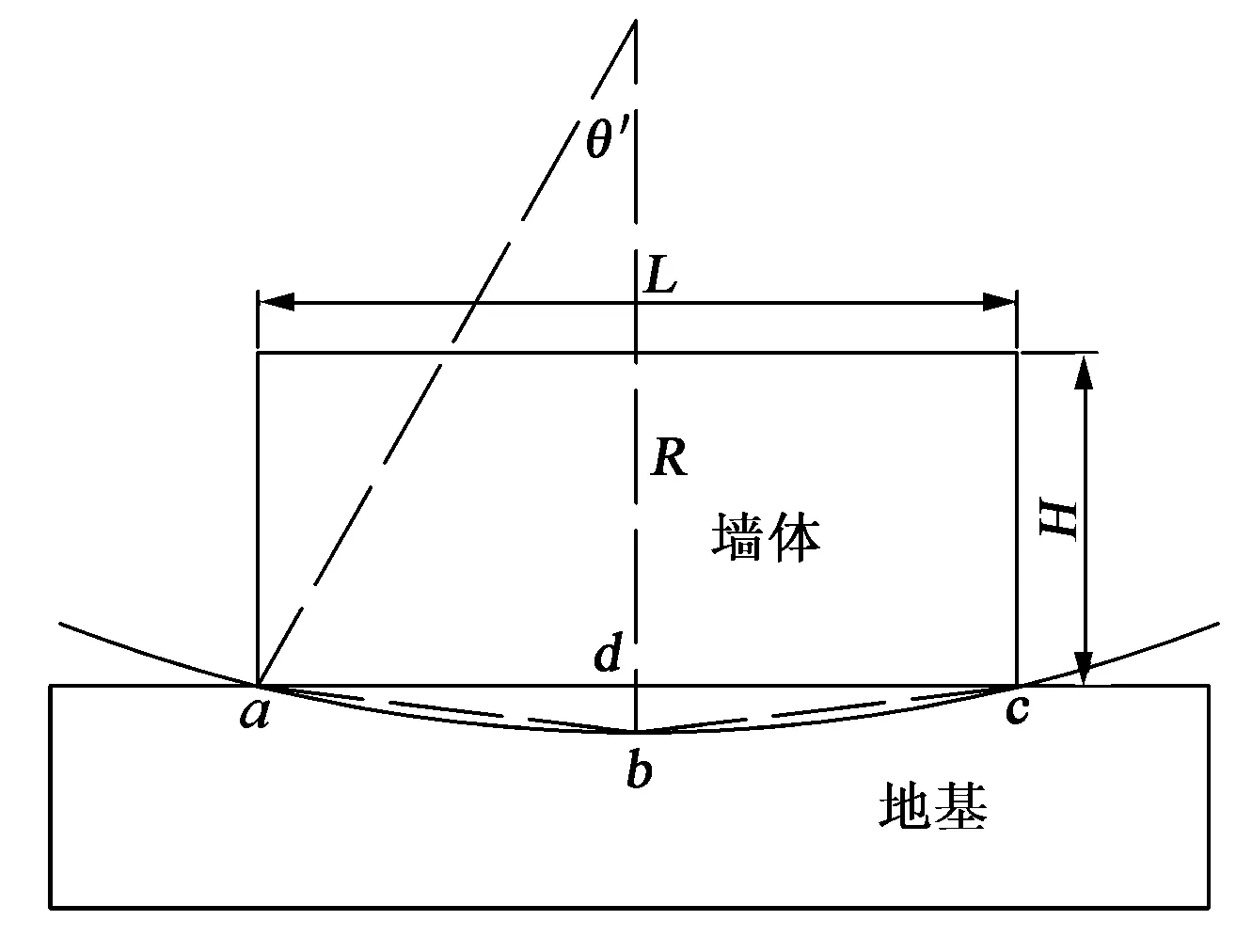
图4 地表负曲率时采空区尺寸模型
图5为某一特定尺寸下,根据以上模型,建立的负曲率影响时不同等级曲率半径与采空区尺寸之间的关系。按照公式(2),4种破坏等级的曲率、曲率半径与模拟采空区最大垂向高度之间的对应关系为:Ⅰ级破坏-曲率0.2mm/m2-曲率半径R1=5000m-采空区最大垂向高度l1=0.125m;Ⅱ级破坏-曲率0.4mm/m2-曲率半径R2=2500m-采空区最大垂向高度l2=0.25m;Ⅲ级破坏-曲率0.6mm/m2-曲率半径R3=1600m-采空区最大垂向高度l3=0.39m;Ⅳ级破坏-曲率0.8mm/m2-曲率半径R4=1250m-采空区最大垂向高度l4=0.50m。
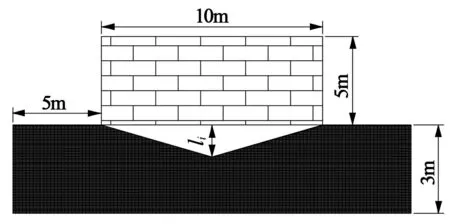
图5 地表负曲率墙体变形有限元模型
根据我国矿区砖砌体结构建筑物的一般情况,结合砌体结构建筑物的相关规范,确定如下地基和墙体的力学性能参数:
(1)地基土体采用D-P材料模式:弹性模量E=2500MPa,泊松比为0.3,密度为2000kg/m3,其他参数见表1。
(2)将墙体看作均匀的各向同性材料,属于非线性弹性材料,服从Mohr-Coulomb屈服准则:弹性模量E=3000MPa,泊松比为0.25,密度为2200kg/m3,其他参数见表1。
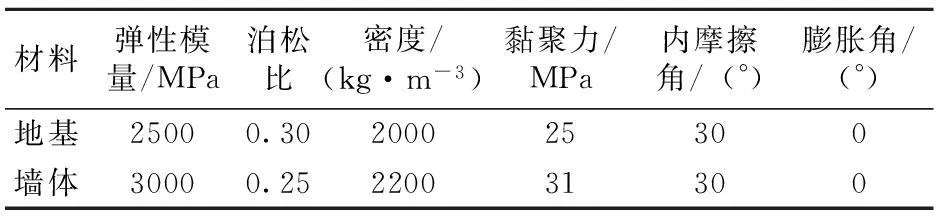
表1 材料的力学参数
数值模拟开挖时,所挖模拟采空区面积按照图3、图5的尺寸进行,在正负曲率的影响下分别进行8个批次的模拟。
2墙体应力变化分析
2.1地表正曲率对墙体的影响
建筑物受到地表正曲率作用,按照砖混结构建筑物破坏的4种等级,分别确定了相应的曲率大小,并根据曲率与近似“采空区”的转换关系,采用有限元分析软件得到墙体应力分布等值线,如图6所示,图中应力的单位为Pa。
从图6中可以分析得出:
(1)在不同破坏等级对应的地表正曲率作用下,墙体的应力分布规律基本相同,随着地表曲率增大,墙体内部应力增大,但应力值在墙体的两端向上部有较大的收敛,继而形成了墙体上部的拉应力集中。
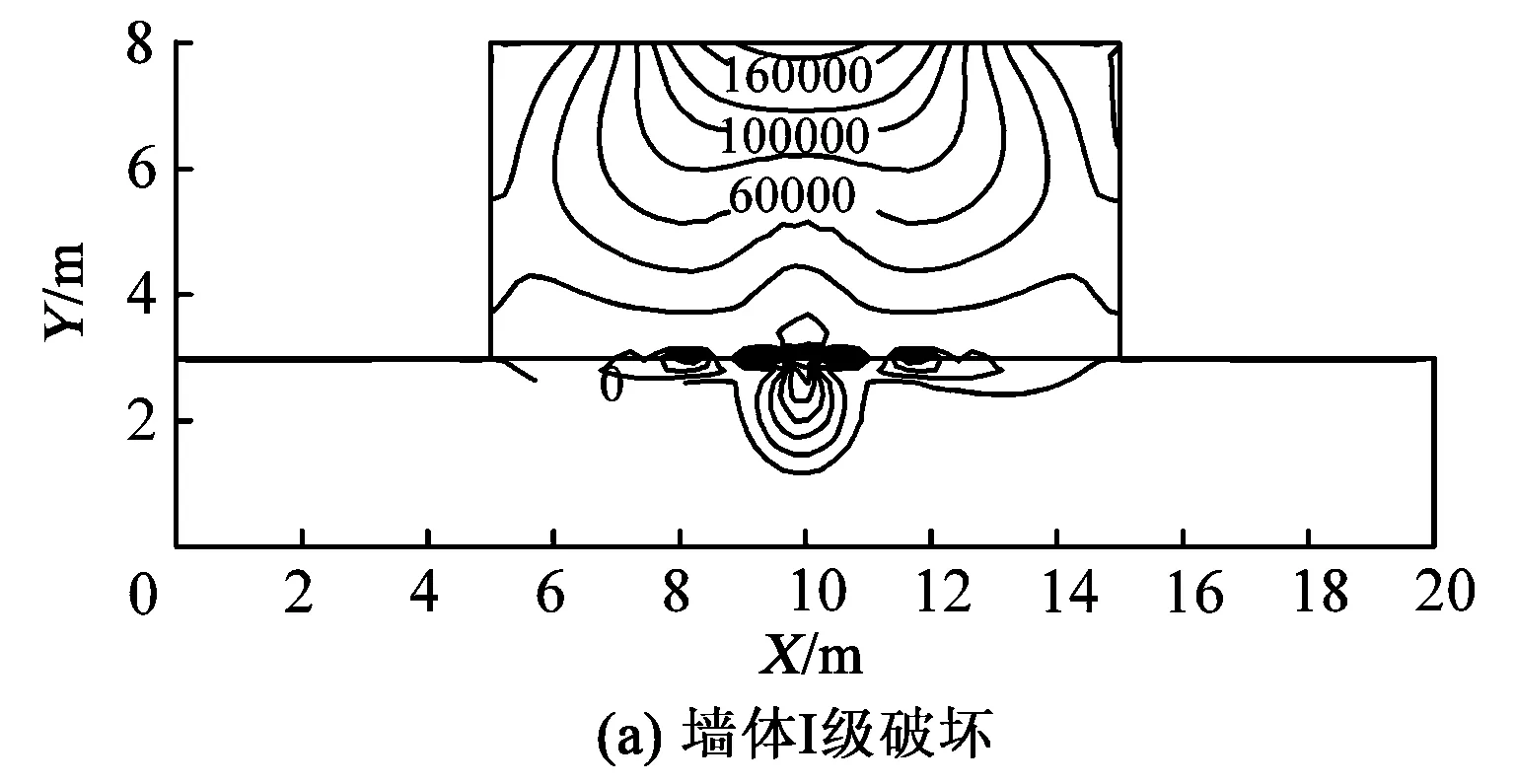
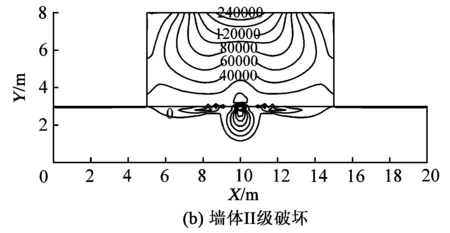
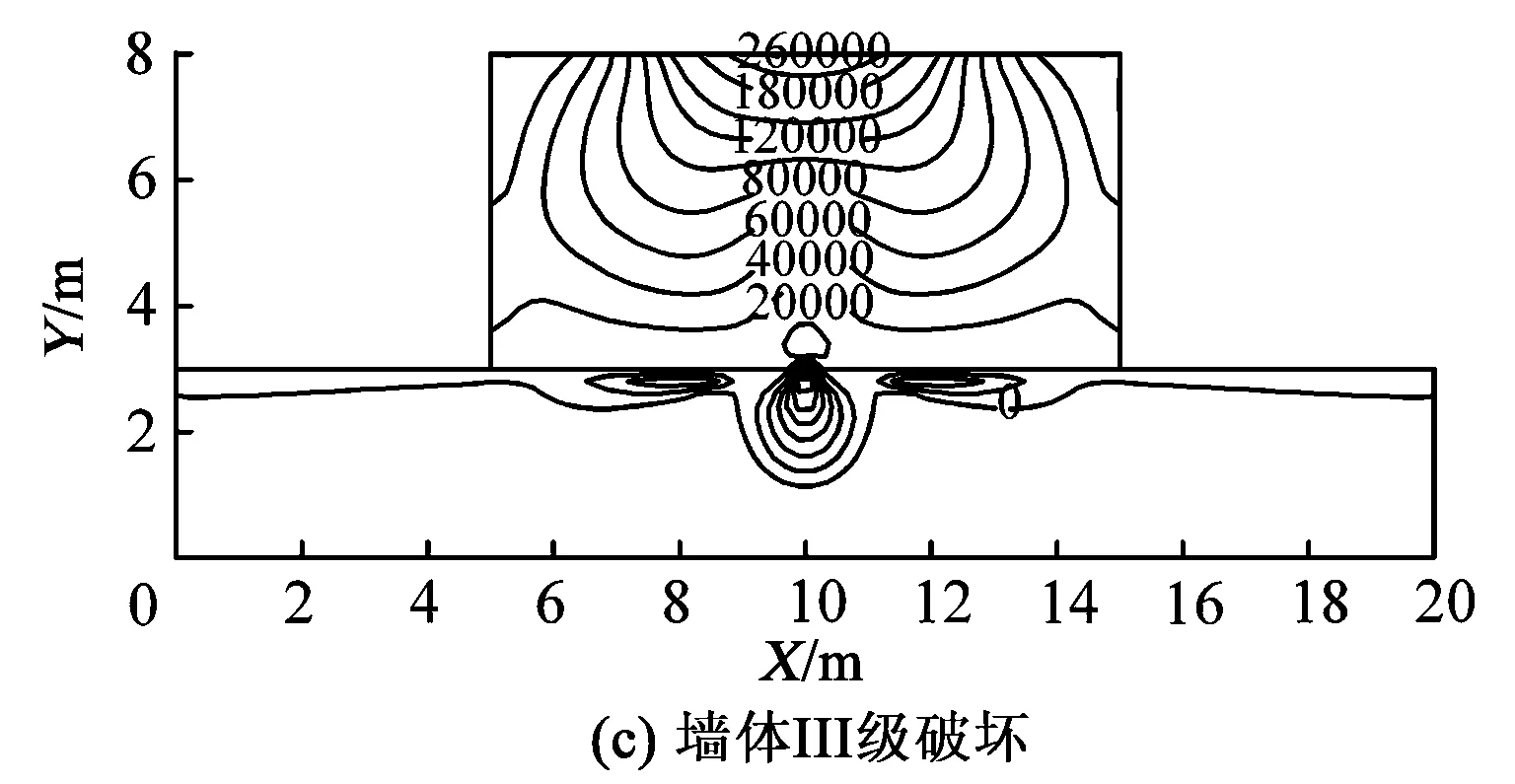
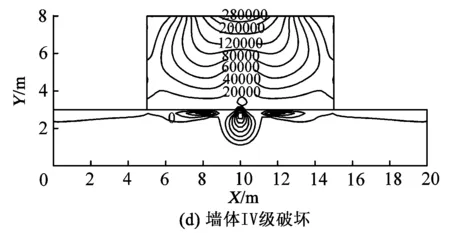
图6 地表正曲率影响的墙体应力分布等值线
(2)地表呈现“凸”型圆弧状时,墙体下沿中心受到支撑作用,两端悬空,故墙体下沿靠近中心处容易发生断裂,而墙体上沿受到拉伸作用,且由两端向中间逐渐增大,当增大到墙体承受的最大极限值时,墙体发生断裂,其最先达到极限值的位置在墙体两侧,此时墙体易形成倒“八”字裂缝,裂缝表现为下窄上宽。
2.2地表负曲率对墙体应力变化的影响
通过有限元分析软件模拟砖混结构建筑物4种破坏等级分别对应的地表负曲率,在近似转换为“采空区”时,墙体的应力变化等值线如图7所示,图中应力单位为Pa。
分析图7可知,在不同等级的地表曲率变形作用下,墙体的应力分布规律基本相同,随着地表曲率变形等级的加大,墙体内部受到的最大应力增大,且墙体受到的相同应力值等值线向外收敛;地表呈现“凹”型圆弧状时,墙体下沿两端受到支撑作用,处于应力集中区域,此处墙体易发生断裂,而墙体上沿受到压缩作用不易发生断裂,但是墙体下沿发生的断裂逐渐向上发展,最终形成正“八”字裂缝,裂缝表现为下宽上窄。
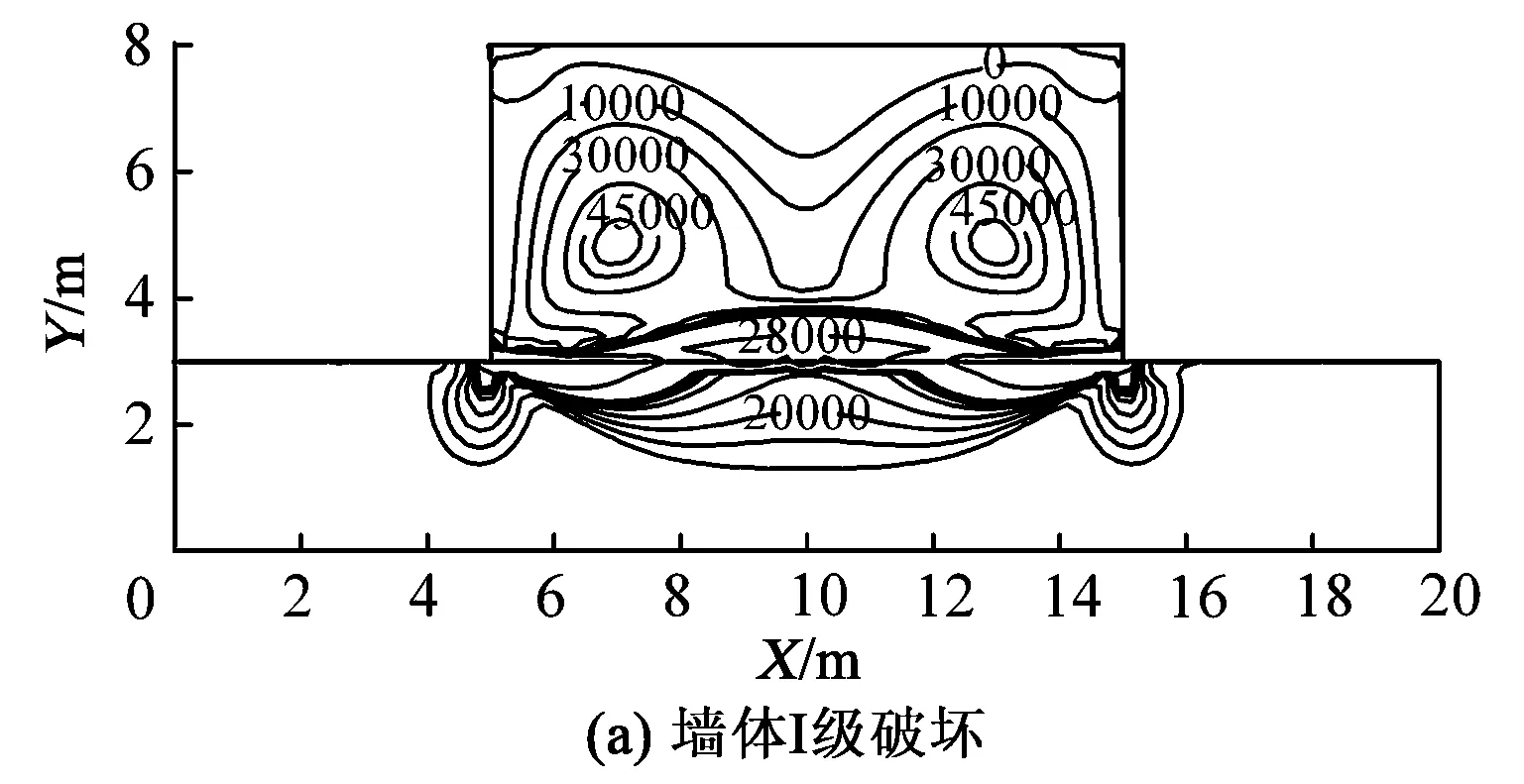
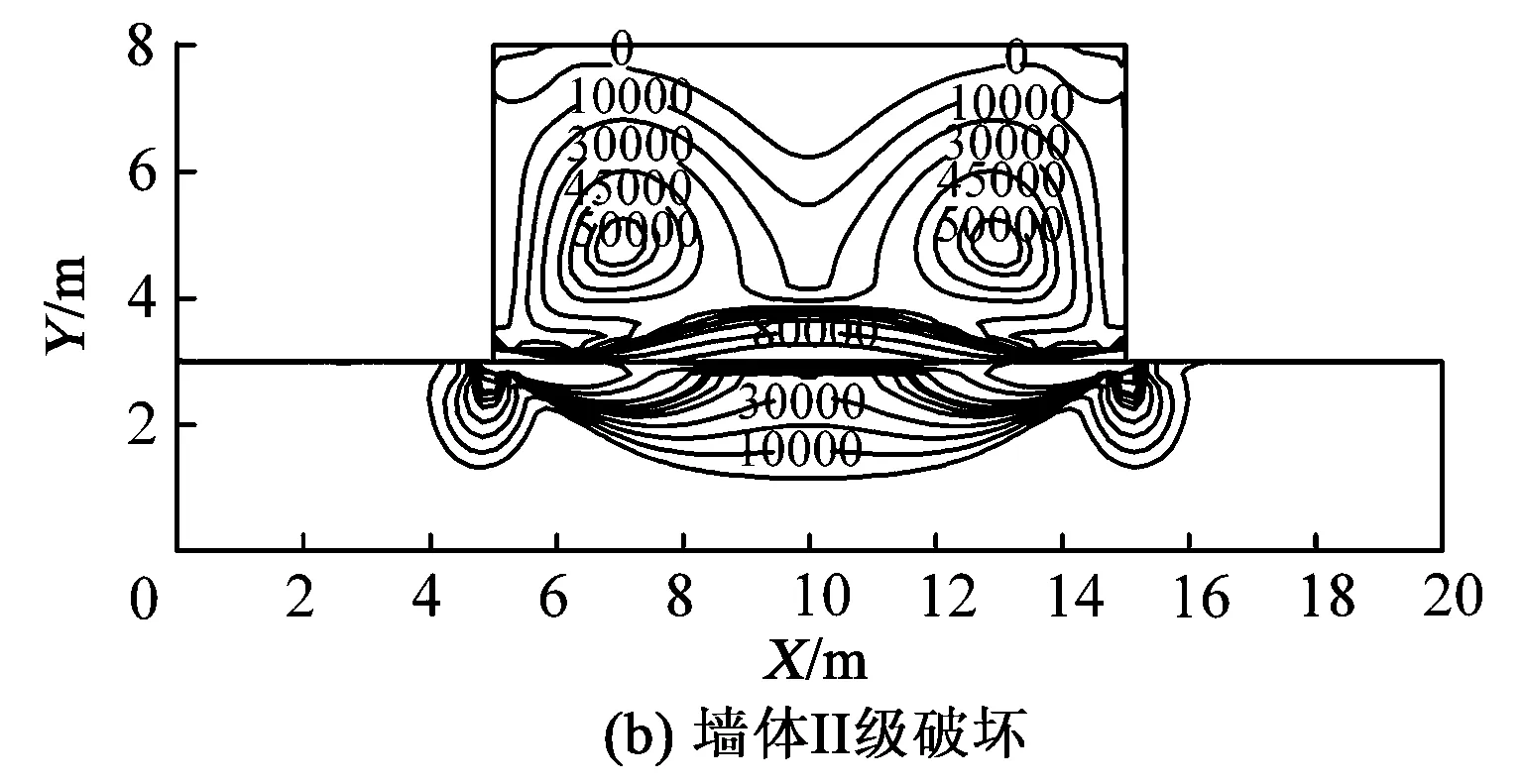
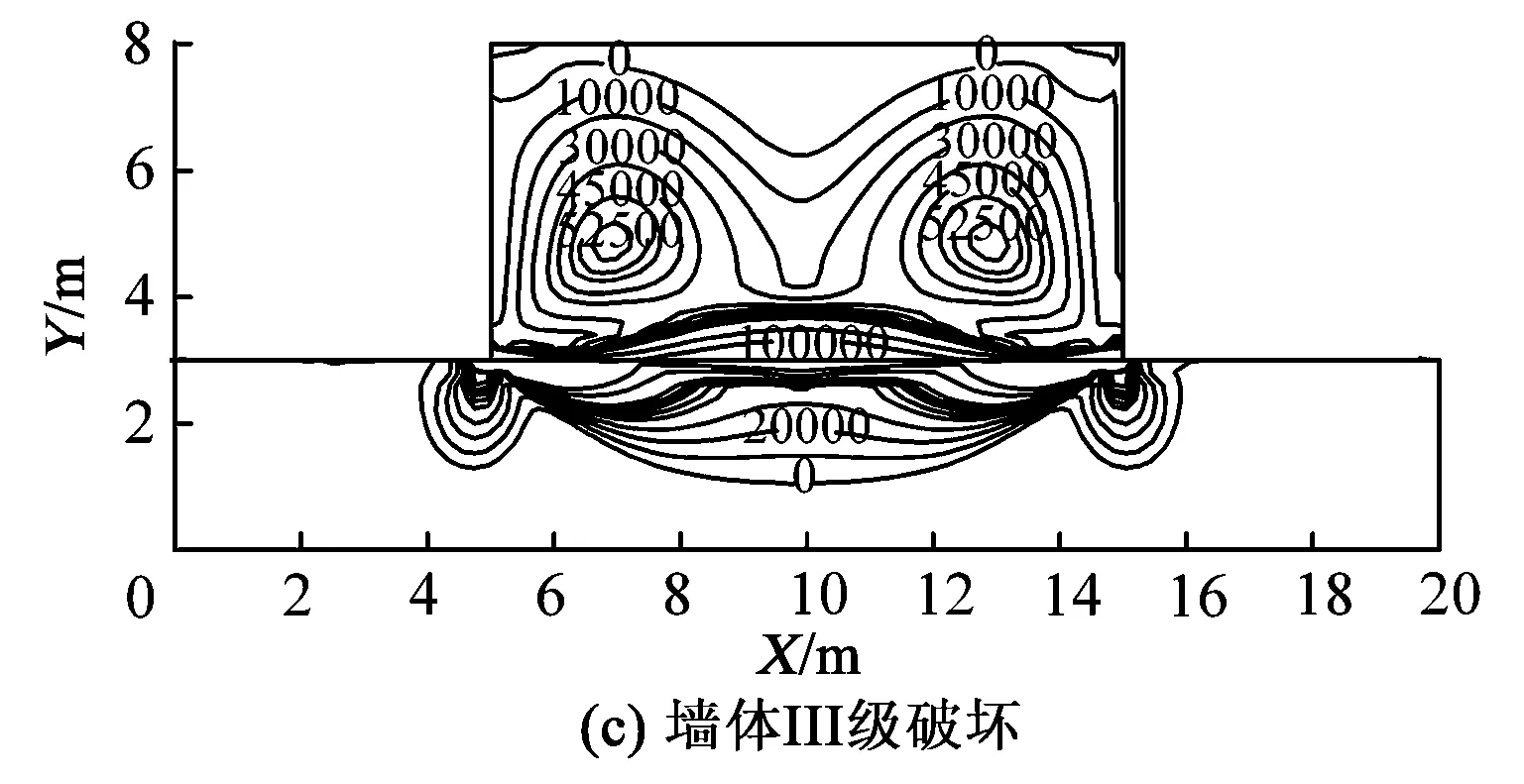
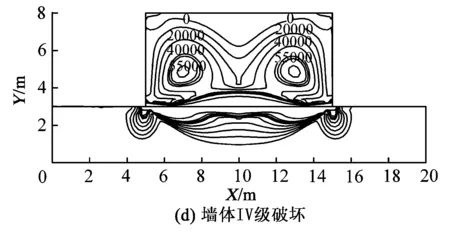
图7 地表负曲率影响的墙体应力分布等值线
3实例验证
女院村位于山西蒲县太林乡附近,2013年受到太林乡某煤矿的开采影响,造成了地表房屋采动损害,811综采工作面位于女院村斜下方,开采时间为2013年,工作面走向长574m,倾斜长128m,开采深度160m,煤层厚度1.8m,近似水平,上覆岩层厚度约为150m,第三、四系黄土层为10~60m。2014年5月对女院村的地表采动损害进行了实地勘查。测定了该典型裂缝墙体的位置、墙体裂缝长度和裂缝宽度,墙体位于采空区外侧边缘,高2m,长5m,裂缝宽度50mm,上下贯通,在墙体上成倒“八”形状,与地表夹角约为50°。女院村房屋损害情况及与采空区的井上下对照关系分别见图8和图9。
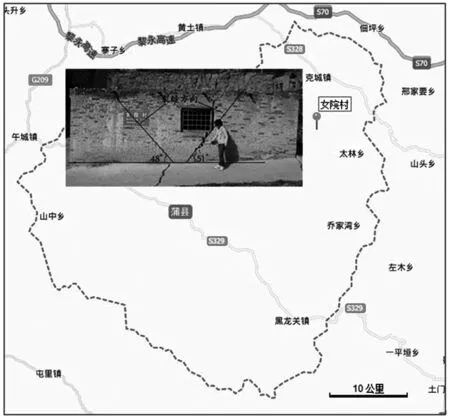
图8 女院村位置分布及墙体裂缝示意
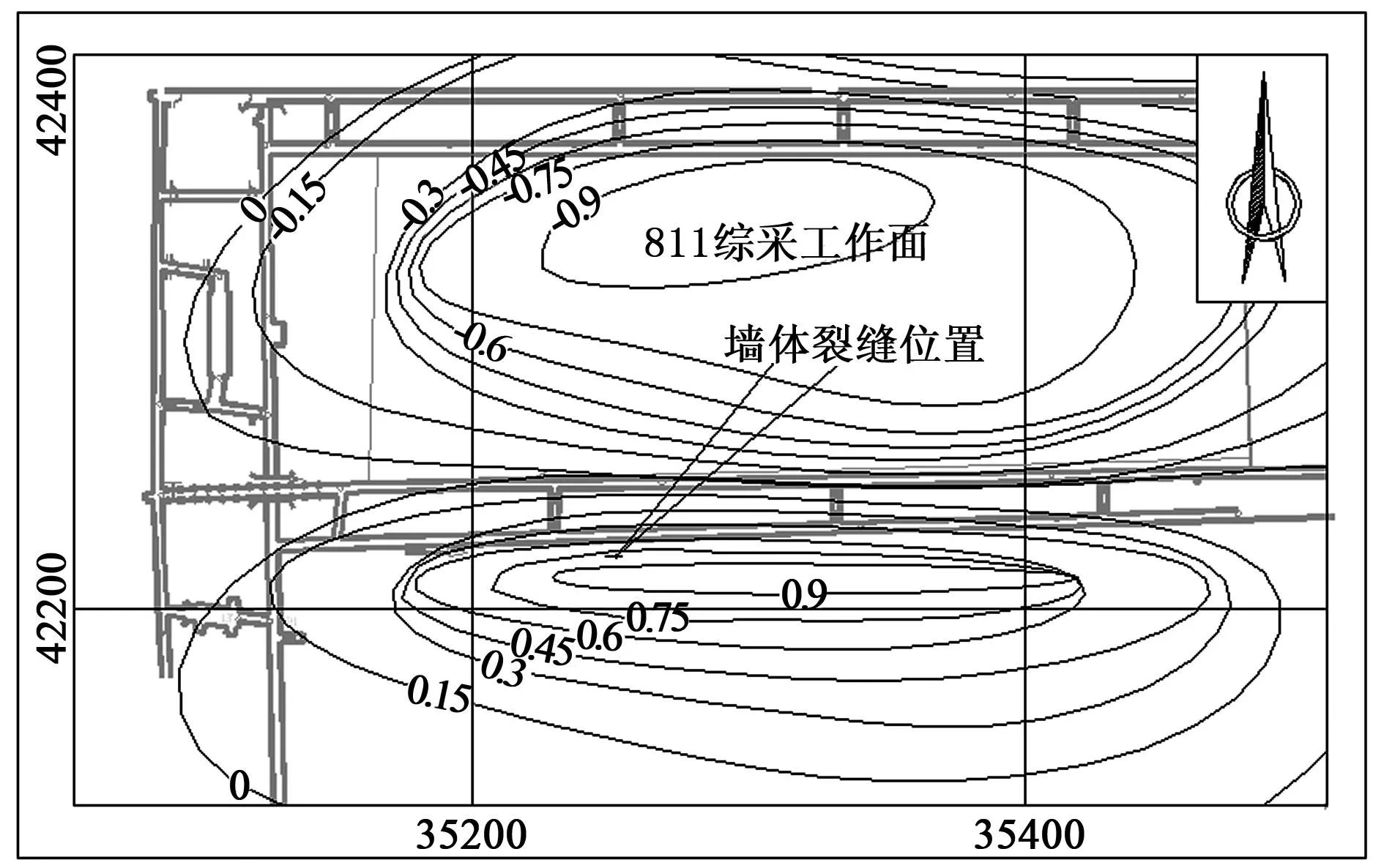
图9 村庄井上下对照图及曲率变形值
为了验证地表曲率对墙体的移动变形与破坏的影响规律,采用山区地表移动变形预计软件系统(MMSPS),预计得到地表曲率变形等值线如图9所示,墙体地基的曲率变形值为0.8mm/m2,按照上述曲率与破坏等级关系模型,属于Ⅳ级破坏,与该墙体的实测破坏等级一致。
4结论
矿山开采沉陷造成岩层及地表移动变形,对地表建构筑物产生了不同程度的影响。为了探究地表曲率变形对建筑物的影响规律,采用数值模拟方法将曲率变形模拟为采空区,对地表墙体的移动变形进行了研究。
(1)建立了正、负曲率条件下,不同地表破坏等级曲率半径与模拟“采空区”间的关系模型,并计算出不同破坏等级时采空区的尺寸大小。建立了砖混结构破坏等级与曲率之间的变形关系。
(2)地表发生正曲率变形时,墙体上沿处于拉伸变形,拉应力集中于上沿中部。墙体基础中部受地基支撑,墙体上部应力较大,下沉应力较小,易形成下窄上宽的倒“八”字裂缝。
(3)地表负曲率变形时,墙体的上沿应力较
小,而下部由于受到拉伸,而形成应力集中区域,且墙体两侧的应力较小,易形成下宽上窄的正“八”字裂缝。
[参考文献]
[1]题正义,刘思杨,屈年华.采动作业下地表移动变形分析[J].辽宁工程技术大学学报(自然科学版),2015,37(6):657-660.
[2]冯宝红.开采沉陷对建筑物影响的分析[J].测绘科学,2013,36(4):170-171.
[3]梁为民,李想,乔俊凤.受采动曲率变形影响的地基对建筑物基础的力学作用[J].矿业研究与开发,2012,32(4):93-96.
[4]刘书贤,魏晓刚,张弛,等.煤矿多煤层重复采动所致地表移动与建筑损坏分析[J].中国安全科学学报,2014,24(3):59-65.
[5]郭麒麟,乔世范,刘宝琛.开采影响下的岩土体移动与变形规律[J].采矿与安全工程学报,2011,28(1):109-114.
[6]陈凯,张俊英,贾新果,等.浅埋煤层综采工作面地表移动规律研究[J].煤炭科学技术,2015,43(4):127-130.
[7]冯军,谭志祥,邓喀中.厚松散层深部宽条带跳采对地表沉陷的影响及应用[J].煤矿安全,2015,46(4):189-191.
[8]赵飞,杨双锁,崔健,等.薄冲积层急倾斜煤层群开采地表移动规律[J].煤矿安全,2015,46(1):40-43.
[9]王刚,郭广礼,李伶.开采沉陷对高等级公路的破坏机理[J].煤矿安全,2011,42(6):169-172.
[10]朱庆伟,蒋军.煤层开采沉陷对桥梁建筑物的影响分析[J].测绘科学,2014,37(4):88-91.
[11]姚文华,宋选民.开采沉陷对地面建筑物的影响研究[J].中国煤炭,2013,34(3):57-59.
[责任编辑:徐乃忠]
上述研究成果表明:采动变形作用下建筑物变形与地基变形之间存在一定关系;采动引起建筑物附加应力存在一定分布规律;采动地表移动变形量中的曲率、倾斜、水平变形对建构筑的影响最大。
[收稿日期]2015-08-19
[作者简介]廉旭刚(1984-),男,山西运城人,讲师,博士,主要从事开采沉陷及变形监测研究与教学工作。
[中图分类号]TD325
[文献标识码]B
[文章编号]1006-6225(2016)02-0033-04
[DOI]10.13532/j.cnki.cn11-3677/td.2016.02.010
[引用格式]廉旭刚,陈胜云,胡海峰.地表曲率变形对房屋墙体损坏的数值模拟研究[J].煤矿开采,2016,21(2):33-36,52.
