地表移动负指数函数预计法的参数确定方法研究
2016-06-08于宪煜胡友健牛瑞卿
于宪煜,胡友健,牛瑞卿
(1.中国地质大学(武汉)信息工程学院,湖北 武汉 430074;2.中国地质大学(武汉)地球物理与空间信息学院,湖北 武汉 430074)
地表移动负指数函数预计法的参数确定方法研究
于宪煜1,胡友健1,牛瑞卿2
(1.中国地质大学(武汉)信息工程学院,湖北 武汉 430074;2.中国地质大学(武汉)地球物理与空间信息学院,湖北 武汉 430074)
[摘要]负指数函数法的预计精度主要取决于其预计参数a,b的精度和可靠性,而采动影响程度(系数) 对参数a,b的影响最大。提出利用矿区下沉典型曲线来建立参数a,b与采动影响系数之间的定量关系并将定量关系式用于确定参数a,b。利用实测数据对所提出的参数确定方法的实用效果进行验证,结果表明:参数a,b与采动影响系数之间存在密切的相关关系,其关系可以用线性函数定量地表示。
[关键词]地表移动预计;负指数函数法;预计参数;采动影响系数
矿山开采可能对位于采动影响范围内的人工地物和自然环境(建筑物、铁路、公路、水体、土地,滑坡体等) 造成有害影响,而地表移动预计可为科学、合理地制订地下开采方案和采取地面防护措施,尽可能地避免或减小地下开采对人工地物和自然环境的有害影响,提供必需的基础资料[1-3]。国内外现已建立并应用的地表移动预计方法有许多种,如典型曲线法[4-5]、概率积分法[6-7]、负指数函数法[8]、威布尔分布函数法[9]、双曲函数型剖面函数法[10]和下沉格网法[11]等。负指数函数法因可以通过变动其预计参数a,b灵活地描述不同分布形态的下沉曲线,具有较高的预计精度且便于进行数学处理,是应用较为广泛的地表移动预计方法之一[8,12-13]。利用该方法进行预计时,必须确定其预计参数a,b,而a,b的数值与采动影响程度(系数)、煤层倾角和上覆岩层的性质有关[12,14]。一般认为,采动影响程度对参数a,b的影响最大[12,15]。因此,严格说来,在某个非充分采动条件下求得的参数a,b的值,只能用于相同的采动影响程度下进行预计。
为了提高负指数函数法的预计精度,已有学者对其预计参数a,b进行了研究。文献[15] 研究了参数a,b的物理意义,结论认为:参数a反映岩性的影响,而参数b反映采动影响程度(系数)的影响。文献[16]分析了参数a,b的确定方法在实际应用中存在的问题,重点讨论了半盆地长度L对所求参数值的影响,并得出了如下结论:确定半盆地长度L的精度不影响确定参数a,b的精度,但是,如果用于确定参数a,b的半盆地长度与用于预计地表下沉曲线所用的半盆地长度不一致,则会降低预计精度。文献[17] 也研究了半盆地长度L对参数a,b的影响,认为选择不同的半盆地长度L对参数b和下沉盆地剖面的形态不产生影响,但L值的差异会引起参数a发生变化。文献[18] 则针对粗差对参数a,b的影响,提出了采用加权最小二乘法确定参数a,b的抗差估计法,并利用实测数据验证了此方法的有效性。
已有相关文献对负指数函数法参数a,b的物理意义及其确定方法进行研究,得出了具有重要意义和参考价值的结论,但尚未研究和建立参数a,b与其主要影响因素——采动影响程度之间的定量关系。因而,目前对负指数函数法参数a,b的变化规律的认识还不够深入和全面。在实际工作中,往往因确定的预计参数a,b存在较大偏差,而使预计的地表移动和变形值产生较大的偏差。为此,本文提出利用矿区下沉典型曲线来研究和建立负指数函数法的参数a,b与采动影响系数之间的定量关系的方法,将其定量关系式用于确定参数a,b并利用实测数据验证采用本文提出的方法确定参数a,b的有效性和实用性。
1预计参数a,b的确定方法
1.1参数a,b与采动影响系数间定量关系的研究
在许多矿区,已经利用开采沉陷监测数据建立了下沉典型曲线,例如河北省的峰峰矿区、河南省的平顶山矿区、山东省的龙口矿区等都已建立其下沉典型曲线[5,8,12-13],前苏联的各主要煤田以及在一个大煤田的不同区域都建立了其下沉典型曲线[19],英国国家煤炭局编制出版了一整套下沉典型曲线[20]。尚未建立下沉典型曲线的矿区,只要在不同采动影响程度下设置过一定数量的地表移动观测站,并进行过较系统的观测,就可以利用观测数据建立其下沉典型曲线。基于此,本文提出利用矿区下沉典型曲线来研究和建立负指数函数法的参数a,b与采动影响系数之间的定量关系的方法。
如图1所示,在倾向主断面内负指数函数法的地表下沉预计公式为(走向与倾向主断面内下沉预计公式相同)[8]:
(1)
式中,x为地表点的横坐标;w(x)为地表点的下沉值;L为半盆地长度;wm为地表最大下沉值;a,b为与地质采矿条件有关的预计参数。
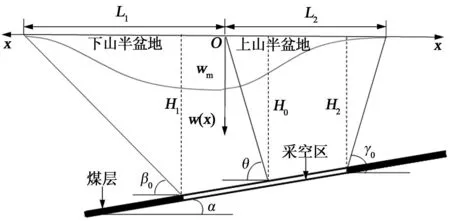
图1 倾向主断面内的地表下沉预计坐标系统和下沉曲线
为便于研究,对公式(1)线性化。将公式(1)两边除以wm,并令Z=x/L可得:
w(x)/wm=e-aZb
(2)
式中,w(x)/wm为下沉分布系数。
对公式(2)两边取对数得:
-lg(w(x)/wm)=aZblge
(3)
再对公式(3)两边取对数得:
lg(-lg(w(x)/wm))=blgZ+lg(alge)
(4)
令X=lgZ,A=lg(alge),Y=lg(-lg(w(x)/wm)),可得:
Y=A+bX
(5)
公式(5)即为公式(1)的线性形式。对于任意一条下沉典型曲线,可组成法方程如下:
(6)
式中,N为点数。
参数b的值可由式(6)直接解得,而参数a可由公式A=lg(alge)反算求得。这样,对于任意一条下沉典型曲线,可以通过最小二乘拟合计算出与其采动影响系数相对应的一组参数a,b。采动影响系数定义为[21]:
n1=k1D1/H0
(7)
n3=k3D3/H0
(8)
式中,n1和n3分别为在煤层倾向方向和走向方向的采动影响系数;D1和D3分别为煤层倾向方向和走向方向的开采尺寸;H0为煤层平均开采深度;k1和k3为介于0和 1之间的系数,其值主要与上覆岩层的性质有关,一般坚硬岩层时取0.7,中硬岩层时取0.8,软弱岩层时取0.9。
采动影响系数与地表充分采动程度之间的关系:n1<1,n3<1,倾向和走向方向均为非充分采动;n1<1,n3>1,倾向方向为非充分采动,走向方向为超充分采动;n1>1,n3<1,倾向方向为超充分采动,走向方向为非充分采动;n1=1,n3=1,倾向和走向方向均达到充分采动;n1>1,n3>1,倾向和走向方向均达到超充分采动。
对于在煤层倾向或走向半盆地内的任意一组下沉典型曲线,可以首先采用上述研究方法分别求出与其采动影响系数相对应的参数a,b的数值;然后,利用统计分析方法建立参数a,b与采动影响系数之间的回归方程,将其用于确定任意采动影响程度下参数a,b的数值。
1.2参数a,b与采动影响系数之间的回归方程
以峰峰矿区倾向主断面内的下沉典型曲线为例,采用前述研究方法建立参数a,b与采动影响系数n1之间的回归方程。该矿区走向主断面大多属于充分采动,倾向主断面大多属于非充分采动,根据多年的开采沉陷实测资料分析求得的倾向主断面下沉典型曲线分布系数w(x)/wm与相应的采动影响系数n1之间的对应值见表1(适用于煤层倾角10~25°)[22]。利用表1中的数据求得参数a,b与采动影响系数n1之间的对应值列入表2,并根据表2中的数据作出a,b与n1之间的相关图,如图2、图3所示。

表1 峰峰矿区倾向主断面内下沉典型曲线分布系数w(x)/wm

表2 参数a,b与采动影响系数n1之间的关系
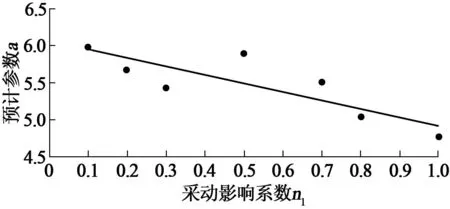
图2 预计参数a与采动影响系数n1的相关性
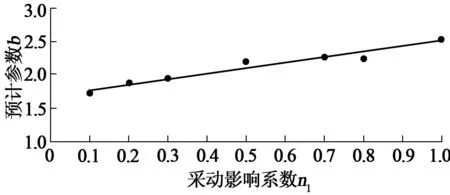
图3 预计参数b与采动影响系数n1的相关性
从图2可以看出,参数a与n1之间的关系可以近似地用线性函数表示为:
a=a0+kan1
(9)
式中,a0为常数;ka为系数。
根据线性回归原理[23],常数a0,ka和相关系数ran可用下列公式计算:
(10)
(11)
(12)
(13)
(14)
式中,M是n1的个数。
回归计算结果为:
a=6.045-1.141n1;ran=-0.839
(15)
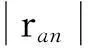
从图3可见,参数b与采动影响系数n1之间的关系也可以近似地用线性函数来表示:
b=b0+kbn1
(16)
式中,b0为常数;kb为系数。
回归计算结果为:
b=1.680+0.822n1;rbn=0.957
(17)

为研究参数a与b之间的相关性,根据表2作出参数a与b之间的相关图(图4)。

图4 预计参数a与b的相关性
从图4可见,参数a与b之间的关系亦可以近似地表示为线性函数:
a=k0+kb
(18)
式中,k0为常数;k为系数。
回归计算结果为:
a=7.999-1.209b;rab=0.764
(19)
取显著性水平α=0.05,以自由度为5查相关系数表得相关系数的临界值rα=0.754。 由于rab>rα,说明a与b之间相关显著,线性回归方程有效。
由以上回归分析可见,负指数函数法的预计参数a,b与采动影响系数之间存在密切的相关关系,参数a与b之间也存在密切的相关关系,回归方程(15)和(17)可以用于峰峰矿区以及地质采矿条件与之类似的矿区确定参数a,b。
2参数a,b确定方法实用效果的验证
某矿在一采区上方设置地表移动观测站,对走向和倾向主断面内的位移和变形进行了监测。开采煤层厚度m=2m;煤层倾角α=10°;走向方向工作面长度D3=350m;倾向方向工作面长度D1=100m;上边界深度H2=137m;下边界深度H1=154m;平均深度H0=145.5m。地表移动基本参数:下沉系数q=0.72;最大下沉角θ=90°-0.7α;上山边界角γ0=65°;采动影响系数n1=0.86D1/H0,n3=0.86D3/H0。
利用该采区倾向主断面内上山方向的地表下沉观测结果,对前述参数a,b的实用效果进行分析和验证。
2.1采动影响系数的计算
n1=0.86D1/H0=0.86×100/145.5=0.59<1,倾向方向为非充分采动。
n3=0.86D3/H0=0.86×350/145.5=2.1>1,走向方向为超充分采动。
2.2参数a,b的计算
a=6.045-1.141n1=6.045-1.141×0.59=5.37181
b=1.680+0.822n1=1.680+0.822×0.59=2.16498
2.3最大下沉值计算
将上面有关计算结果代入公式(1)得到倾向主断面内下沉预计公式为:
(20)
公式(20)中的半盆地长度L可按下式求得:
L=H2cotγ0+1/2D1cosα+H0cotθ=
137cot65°+1/2×100cos10°+145.5cot(90°-0.7×10°)=131(m)
利用公式(20)计算的上山方向地表下沉分布系数(w(x)/wm) 见表3,将实际测量的下沉分布系数(w(x)′/wm) 及其与计算结果的差值((w(x)-w(x)′)/wm)也列入表3,并作出计算和实测的下沉分布曲线如图5所示,以便于对计算结果与实测结果进行直观的比较。
从表3可知,计算下沉值与实测下沉值的最大差值为最大下沉值(1106mm)的2.2%,即24mm,求得计算结果的中误差为最大下沉值的1.2%,即13mm,说明计算结果有很高的精度。另外,从图5可以直观地看出,计算下沉曲线与实测下沉曲线的形态一致,两者重合很好。由此可见,采用本文提出的方法确定参数a,b具有有效性和实用性。

表3 上山半盆地主断面内下沉分布系数计算结果与实测结果的比较
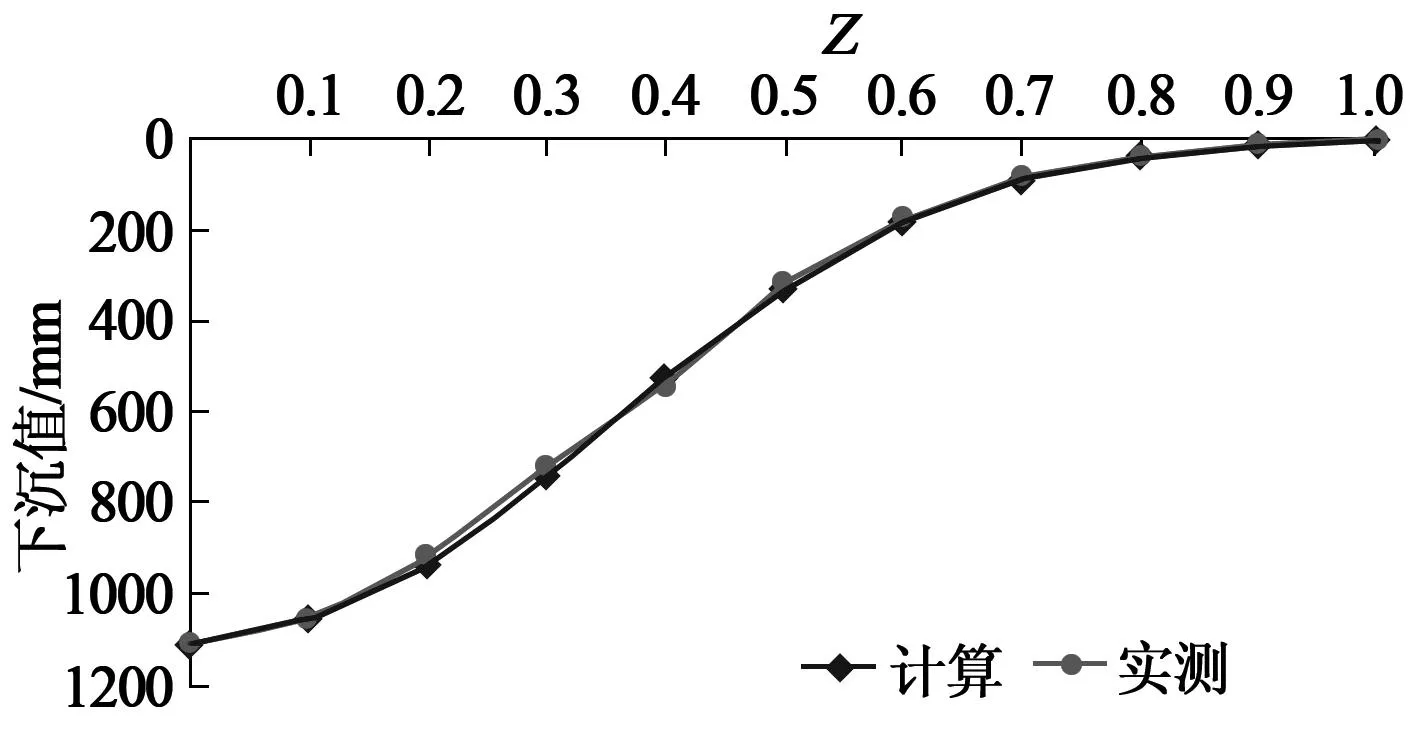
图5 上山半盆地主断面内计算下沉曲线与实测下沉曲线的比较
3结论
通过对负指数函数法的预计参数a,b与采动影响系数之间的关系进行定量的分析和研究,并利用实测数据对本文提出的参数a,b确定方法的实用效果进行验证,可得出如下结论:
(1)负指数函数法的参数a,b与采动影响系数之间存在密切的相关关系,其关系可以用线性函数定量地表示。
(2)参数a,b不是彼此孤立地变化的,它们之间存在密切的相关关系,且其关系也可以用线性函数定量地表示。
(3)利用矿区的下沉典型曲线,采用最小二乘拟合法建立参数a,b与采动影响系数之间的回归方程,将其用于确定任意采动影响程度下参数a,b的数值,具有有效性和实用性。
应当指出,负指数函数法的预计参数a,b除了与采动影响程度密切相关之外,还与煤层倾角和上覆岩层的性质有关,因此,本文建立的参数a,b与采动影响系数之间的回归方程,只适用于峰峰矿区和地质采矿条件与之类似的矿区。在其他矿区,可以利用其下沉典型曲线,采用本文提出的方法建立参数a,b与采动影响系数之间的回归方程。另外,负指数函数法仅适用于矩形或接近于矩形的采区。
[参考文献]
[1]P.P.Bahuguna a,A.M.C.Srivastava a and N.C.Saxena.A critical review of mine subsidence prediction methods[J].Mining Science and Technology,1991,13(91):369-382.
[2]郭广礼,王悦汉,马占国.煤矿开采沉陷有效控制的新途径[J].中国矿业大学学报,2004,33(2):150-153.
[3]邹友峰,胡友健,郭增长.采动损害与防护[M].徐州:中国矿业大学出版社,1996.
[4]A Chrzanowski,AS Chrzanowski.Comparison of empirical and deterministic prediction of mining subsidence[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics ,1987,24(5): 214.
[5]张惠生,顾伟.典型曲线法在山东龙口软岩煤矿区开采沉陷预测中的应用[J].地质找矿论丛,2014,29(1):84-90.
[6]刘宝琛,廖国华.煤矿地表移动的基本规律[M].北京:中国工业出版社,1965.
[7]谷金锋,高振森.概率积分法在矿区开采沉陷预测中的应用[J].矿山测量,2011(2):47-49.
[8]周国铨.建筑物下采煤[M].北京:煤炭工业出版社,1983.
[9]何国清.岩移预计的威布尔分布法[J].中国矿业学院学报,1988(1):8-15.
[10]King,H.J.and Whetton,J.T.Mechanics of mine subsidence[C].Proc.European Congr.on Ground Movement,1957.
[11]G.Brauner.Calculation of ground movement in European coalfields[C].Proceeding of symposium on subsidence in mines. Australia:1973.
[12]曹志伟,翟厥成.岩层移动与“三下”采煤[M].北京:煤炭工业出版社,1986.
[13]刘占魁,刘冰蕾,王瑞智.国内矿山开采沉陷的主要研究方法及应用情况[J].西部探矿工程,2011,26(1):176-178.
[14]袁力,郑志刚,滕永海.地表移动预计参数与地质采矿因素的相关关系[J].矿山测量,2014(2):75-77.
[15]曾卓乔.地表移动计算负指数函数法参数的物理意义及其正确运用[J].矿山测量,1980(2):27-34.
[16]张玉呆.负指数函数法a,b系数确定方法探讨[J].同煤科技,2010(4):32-38.
[17]寇新建.半盆地长L对a,b参数的影响[J].矿山测量,1991(4):27-29.
[18]张国卿.负指数函数中待定参数a,b的抗差解法[J].勘察科学技术,1999(5):54-56.
[19]Акимoв.А.Г.Земисев.В.Н.Сдвижение горных пород при подземной разработке уголъных и сланцевых месторождений[M].Москва:Недра,1970.
[20]National Coal Bord.Subsidence Engineers’Handbook[M].London:National Coal Bord(U,K),1978.
[21]郭广礼.矿山开采沉陷及其防治[M].徐州:中国矿业大学出版社,2012.
[22]马伟民,王金庄,聂孟荀,等.煤矿岩层与地表移动[M].北京:煤炭工业出版社,1981.
[23]张正禄,黄声享,岳建平,等.工程测量学[M].武汉:武汉大学出版社,2013.
[责任编辑:施红霞]
Parameters Determination of Negative Exponential Function Forecast of Surface Movement
YU Xian-yu1,HU You-jian1,NIU Rui-qing2
(1.Information Engineering Faculty,China University of Geosciences(Wuhan),Wuhan 430074,China;2.Geophysics & Geomatics Institute;China University of Geosciences(Wuhan),Wuhan 430074,China)
Abstract:The predicting precision of negative exponential function method is mainly depended on precision and reliability of parameters a and b,the largest influencing factor that to parameters a and b is mining influence degree,and quantitative relation of parameters a and b and mining influencing coefficient was put forward on the basis of typical subsidence curve of coal mine area,then parameters a and b were determined by the quantitative relation expression.The practical effects of the parameters determination method was validated by measured data,the results showed that the relations of parameters a,b and mining influence coefficient could be quantitative expressed by linear function.
Key words:surface movement predicting;negative exponential function method;predicting parameters;mining influence coefficient
[收稿日期]2015-08-19
[作者简介]于宪煜(1987-),男,湖北武汉人,在读博士研究生,研究方向为变形监测与灾害地质。
[中图分类号]TD325.2
[文献标识码]A
[文章编号]1006-6225(2016)02-0010-05
矿山开采沉陷规律与变形控制
[DOI]10.13532/j.cnki.cn11-3677/td.2016.02.004
[引用格式]于宪煜,胡友健,牛瑞卿.地表移动负指数函数预计法的参数确定方法研究[J].煤矿开采,2016,21(2):10-14.
