地表残余沉陷变形机理数值模拟与预计参数分析
2016-06-08易四海
易四海
(中煤科工集团 唐山研究院有限公司,河北 唐山 063012)
地表残余沉陷变形机理数值模拟与预计参数分析
易四海
(中煤科工集团 唐山研究院有限公司,河北 唐山 063012)
[摘要]采用数值模拟计算,通过对覆岩移动过程的模拟研究,指出了地表沉陷由岩体变形破坏到岩体密实沉陷的发展过程,揭示了岩体密实沉陷延续是引起地表残余沉陷变形的机理;通过对岩体密实阶段地表沉陷分布规律的模拟研究,证实地表残余变形可以用概率积分法进行预计。根据数值模拟及现场实测数据,确定了长壁开采条件下地表残余沉陷变形的概率积分法预计参数。
[关键词]残余沉陷变形;数值模拟;沉陷过程;预计参数;长壁开采
开采沉陷延续时间较长,地表将在很长时间内存在残余沉陷变形,对采煤塌陷区地表新建建(构)筑物产生不利影响。因此,了解和掌握采煤塌陷区地表残余沉陷规律十分重要。但是,限于采煤塌陷区地表残余沉陷延续时间长、数值较小,一般难以用实测方法掌握其全部发展规律。目前,对采煤塌陷区地表残余沉陷变形的预测已有了一些研究[1-3],对采煤塌陷区建设利用具有一定的指导意义,但在对残余沉陷变形预测参数取值时大多凭经验,缺乏足够的理论支持,给采煤塌陷区地表建筑带来了一定的安全隐患。
为此,本文采用数值模拟计算,研究覆岩移动过程及地表残余沉陷变形的分布规律,依据实测数据建立地表残余沉陷变形的预计方法并确定相关参数,为采煤塌陷区地表安全利用提供理论依据。
1采煤沉陷数值模拟
采用离散元法进行模拟试验。试验设计煤层采厚M=3.0m,采宽L=125m,倾角α=0°,采深H0=100m,松散层厚度Hs=20m,基岩厚度Hj=80m,基岩由砂岩、泥岩和砂质泥岩等岩性组成。图1为数值计算模型网格剖分图。

图1 数值计算模型剖分
1.1地表沉陷过程
地下煤层采出后引起的地表沉陷是一个时间和空间过程。由于地表沉陷孕育与发展过程非常复杂,许多学者从不同的角度对其进行了研究[4-6],这些研究多从地表点的移动量及剧烈程度的角度进行描述。而实际上,地表移动是岩层移动的延伸和表象,岩层移动是发生在岩体内部的力学现象,只有从岩层移动的角度来研究地表沉陷过程才能真实揭示岩层与地表移动的机理与规律。
图2为数值模拟采空区上方不同高度岩层内测点从开采至沉陷稳定时的下沉量变化曲线。该曲线簇可解读为岩层内测点下沉量随时间的变化。由图2可以看出,上覆岩体在开采之初,岩体下沉迅速,经过一段时间后,岩体下沉变化趋缓,直至沉陷最终收敛于某一最大固定值。表1统计了工作面开采至计算结束覆岩的下沉量及下沉增量。根据覆岩下沉量及下沉增量,从岩层移动的角度,可以将采动沉陷过程分为3个阶段。
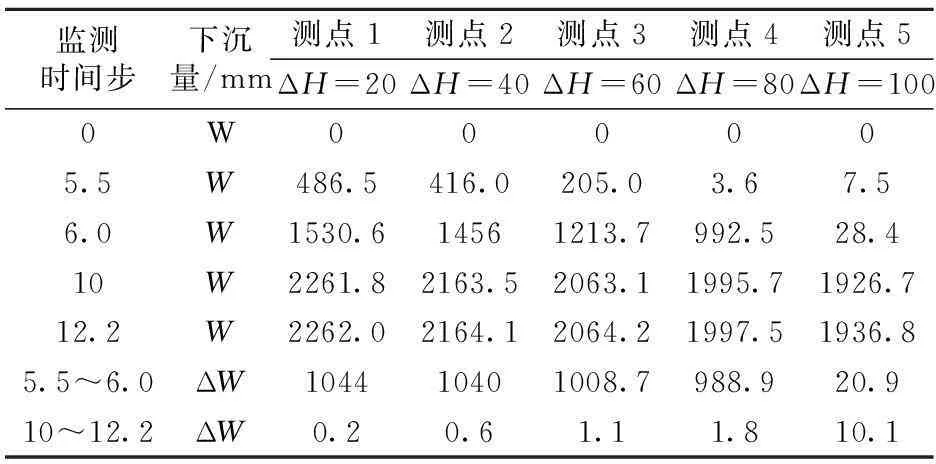
表1 采动过程中覆岩下沉量及下沉增量
注:ΔH为岩层距煤层顶板高度,m;W为下沉量;ΔW为下沉增量。
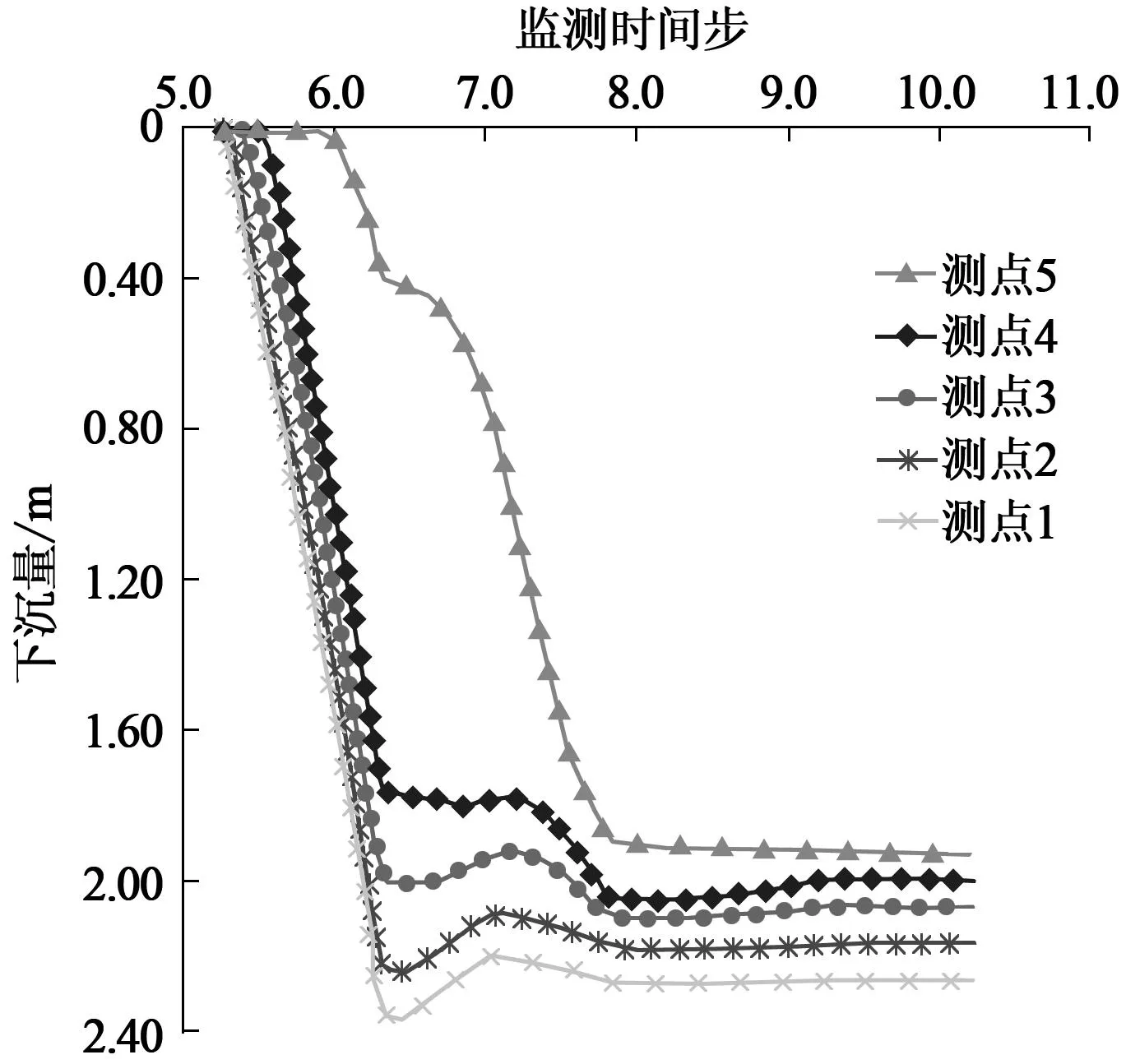
图2 岩层内测点下沉量随时间变化曲线
前一阶段为煤层开采至停采之初(大致为0~6个监测时间步),该阶段覆岩沉陷量迅速增大,如采空区上方20m岩层下沉由开始的0mm增至5.5个时间步时的486.5mm,到第6个时间步时则迅速增至1530.6mm;开采沉陷在向地表传播的过程中,覆岩沉陷增量自下往上递减,至地表时值最小,如采空区上方20m,40m,60m,80m,100m岩层沉陷量从5.5至6个时间步时分别增加了1044m,1040m,1008.7m,988.9m,20.9m,增加值由下往上递减。究其原因是因为此阶段覆岩在一系列复杂的受力变形时空变化后,在竖向上形成明显的“三带”(垮落带、断裂带和弯曲带)破坏特征[7-8],“三带”覆岩内产生大量新生空间(空洞、裂缝、离层),使得覆岩移动在向地表传播的过程中出现衰减。从力学机理上讲,该阶段地表沉陷来源于煤层开采致上覆岩体力学失稳,覆岩相继发生一系列变形破坏(冒落、断裂、弯曲)引起的。因此,可定义该阶段为岩体变形破坏阶段。
后一阶段为工作面停采一段时间后(大致为9个监测时间步之后),该阶段覆岩沉陷量缓慢增加,如采空区上方20m岩层下沉由10至12.2个时间步时只增加了0.2mm;开采沉陷在向地表传播的过程中,覆岩沉陷增量则由下至上累积增加,如采空区上方20m,40m,60m,80m,100m岩层沉陷量从10至12.2个时间步时分别增加了0.2m,0.6m,1.1m,1.8m,10.1m,增加值由下往上递增。这是因为此阶段覆岩内残留的空洞、离层、裂缝等空隙逐渐被压实,覆岩移动是由覆岩内残留的空洞、裂缝、离层等空隙再压实引起的[9]。从力学机理上讲,该阶段地表沉陷主要是由于上覆岩体应力重新得到恢复,岩层在上覆荷载作用下岩体逐渐密实后产生的。因此,可定义该阶段为岩体密实沉陷阶段。
中间阶段大致在6~9个监测时间步,此阶段覆岩移动虽然依旧发育,但明显由剧烈变缓慢,下沉速度衰减很快。此阶段,覆岩应力由卸载状态逐渐向自然重力恒载状态恢复,在竖直方向上覆岩移动是由变形破坏和密实混合产生的,为岩体变形破坏到岩体密实沉陷的过渡阶段。
根据“三下”采煤规程[9]定义,地表残余沉陷为地表在“移动期结束”后还将可能产生的少量残余下沉和变形值。地表的残余沉陷阶段下沉速度缓慢,岩体应力应恢复至自然重力恒载状态,残余沉陷变形主要由岩体在自然重力恒载状态密实引起,数值模拟反映的覆岩移动过程可以看出,地表残余沉陷是岩体密实沉陷延续在地表的一种显现。
1.2岩体密实沉陷阶段地表沉陷变形分布规律
为更好体现采空区破裂岩体的密实效果,在模拟工作面开采计算达到平衡状态后,对地表进行了均布加载,模拟地表建筑荷载,荷载大小为18 kN/m,范围为整个上部自由边界。
图3为数值模拟在均布加载作用下采空区覆岩下沉云图。由图3可以看出,在竖直方向上,采空区上覆破碎岩体内残留空隙由于在均布加载作用下进一步密实,岩体沉陷量由下至上累积增加,至地表值最大;在水平方向上,覆岩移动量整体符合“中间大,两侧边缘小”的特点,这是由于采空区上方覆岩移动量主要是由荷载作用下的空隙再压实引起的;煤柱上方覆岩移动量则是由荷载作用下岩层的压缩引起的。但在采空区上方地表,边缘附近移动量明显比其他区域要大,这主要是由于采空区边缘附近存在较多的空洞。

图3 均布加载作用下采空区覆岩下沉
图4为在均布加载作用下采空区上方地表移动及拟合曲线。由图4可以看出,采空区在地表均布加载作用下,地表下沉分布仍为中部下沉量大、两侧边缘下沉小的盆形特点,只在采空区边缘附近下沉量比采空区中央大,但整体符合正态分布。概率积分法的拟合结果为:拟合下沉系数0.14,拟合的最大下沉值比模拟的值偏大;拟合水平移动系数0.25,拟合的最大水平移动值比模拟的值大;拟合主要影响角正切为1.5,值偏小;拐点偏移距为0.05倍采深,外偏。拟合结果证明概率积分法总体上能够较好拟合地表移动曲线,大体上反映了岩体密实沉陷阶段地表移动与变形的分布情况。
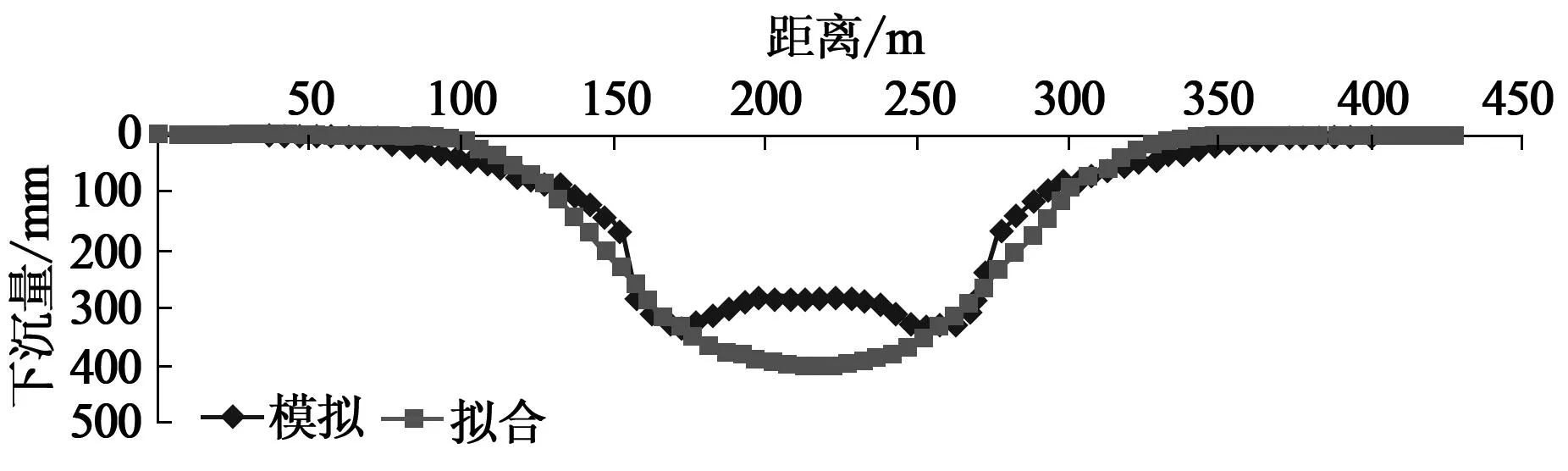
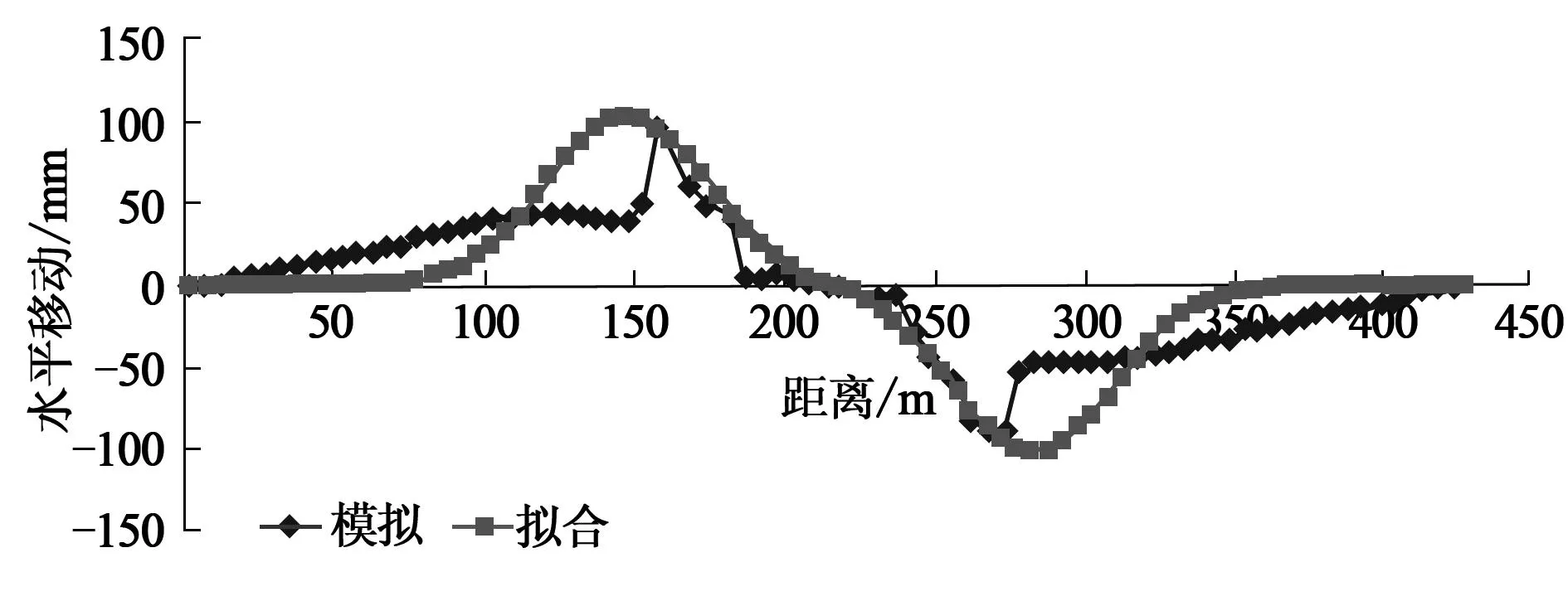
图4 均布加载作用下采空区上方地表移动曲线
2地表残余沉陷计算参数分析
地表残余变形作为岩体密实沉陷延续在地表的显现,可以用概率积分法进行预计,再综合考虑各种因素,确定长壁开采条件下地表残余沉陷计算参数。
(1)残余下沉系数qr大量现场实测数据表明,对于长壁工作面正规大面积开采而言,残余下沉系数主要与开采结束后延续时间密切相关,工作面停采时间越长,其剩余的残余沉陷量越小。残余下沉系数与时间的关系也体现了地表残余变形的时间发育规律。
模型试验、实测数据表明,残余下沉系数与开采结束后延续时间成负指数函数关系递减,其拟合公式可表示为:
qr(t)=a·e-bt
(1)
式中,a为地表最终残余下沉系数;b为地表残余下沉收敛系数。
目前,大多数学者[9,11-12]对其拟合多取工作面停采后的实测数据,致使a,b取值相差悬殊,不具备推广应用价值。究其原因,主要是未从机理上认清地表残余沉陷变形的沉陷本质,将时间参数t设定为工作面停采时间,拟合数据包含了岩体变形破坏及过渡阶段的地表沉陷实测数据。而实际上,地表残余沉陷变形是岩体密实沉陷延续在地表的一种显现,在对地表移动有限时间段内实测数据进行地表残余变形概率积分法拟合求参时,应剔除掉地表沉陷进入岩体密实沉陷阶段之前的伪数据。时间参数t应从地表沉陷进入岩体密实沉陷阶段算起更为合适,即:
qr(t)=a·e-b(t-t0)
(2)
式中,t0为工作面停采至地表沉陷进入岩体密实沉陷阶段的时间,a。
(2)拐点偏移系数S/H采空区开采结束后,采空区边界煤壁附近存在大量的空洞、裂隙及顶板形成悬臂结构,致使开采后地表移动基本稳定时的下沉曲线拐点位于采空区内侧一定距离,这就是拐点偏距,用拐点偏移系数S/H反映。据“三下”采煤规程,当覆岩类型分别为坚硬、中硬、软弱时,开采基本稳定的S/H取值分别为0.31~0.43,0.08~0.30,0~0.07。
随着开采后结束时间的延长,采空区边界的空洞、裂隙及顶板悬臂结构在自重荷载作用下会逐渐压密,产生地表残余沉陷变形。因此,计算采空区地表残余沉陷时的拐点偏移系数可参照基本稳定时的参数稍微取小。
(3)主要影响角正切tanβ残余沉陷时的主要影响角正切tanβ不随开采结束后时间的延长而变化,其取值参照常规沉陷变形的tanβ。据“三下”采煤规程,当覆岩类型分别为坚硬、中硬、软弱时开采基本稳定的tanβ取值分别为1.2~1.91,1.92~2.40,2.41~3.54。
(4)水平移动系数b残余沉陷时水平移动系数b取值参照常规沉陷变形的b的取值。据“三下”采煤规程,地表开采基本稳定时b为0.2~0.3。
(5)开采影响传播角θ残余沉陷时的开采影响传播角θ取值参照常规沉陷变形的θ值。据“三下”采煤规程,θ=90°-kα(α为煤层倾角),当覆岩类型分别为坚硬、中硬、软弱时的0.7~0.8,0.6~0.7,0.5~0.6。
3实例
山西某矿长壁综放工作面,煤层采厚平均为6.5m,倾角3°左右,采深平均为316m,采宽248m,推进长度约1750m。图5为综放工作面停采后实测的走向观测线地表下沉增量图。
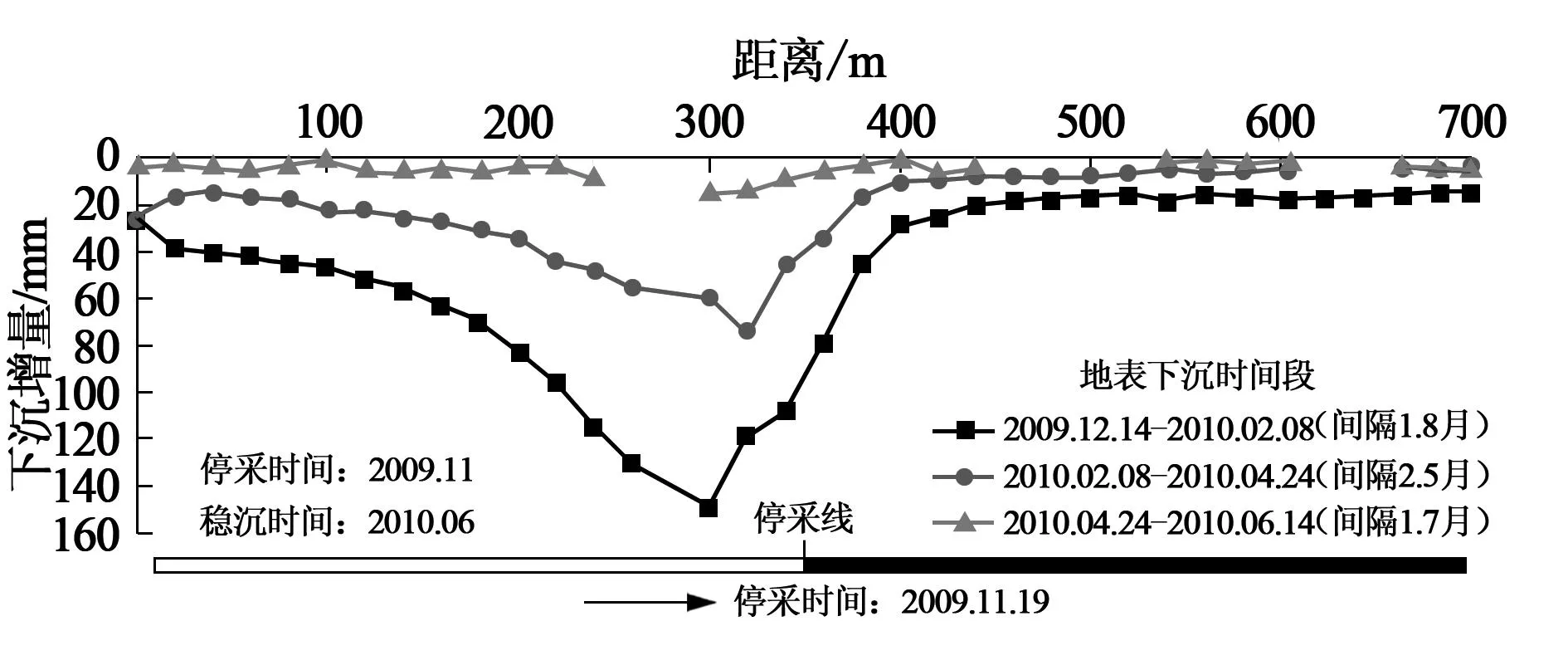
图5 停采后实测走向观测线地表下沉增量
由图5可以看出,在工作面停采后的头几个月,地表下沉呈现量大且剧烈的特点,这主要是新开采空间引起岩体变形破坏后在地表的显现;至工作面停采约0.43a后,地表下沉呈现量小且缓慢的特点,可以看作是岩体在应力平衡后逐渐密实在地表的显现。实测数据表明,综放开采工作面地表沉
陷过程大致在工作面停采后0.43a由岩体变形破坏阶段过渡到岩体密实沉陷阶段,而该工作面稳沉时间实测为7个月。因此,根据不同阶段地表的移动显现特征,并结合现场实测数据,可以初步认定地表沉陷进入岩密实沉陷阶段的时间点为工作面停采之后及稳沉之前的某个时间点。
对该工作面走向观测线110号测点实测下沉数据拟合求取残余下沉系数。
若对工作面停采后的实测数据进行拟合,求得残余下沉系数:
qr(t)=0.184·e-23.0t
(3)
若对工作面停采0.43a后的实测数据进行拟合,求得残余下沉系数:
qr(t)=0.039·e-0.36(t-0.43)
(4)
表2为工作面停采后110号测点累计下沉量实测数据与预计结果比较。由表2可知,同一实测参数,由于拟合数据选取范围不同,式(4)与式(3)中b取值相差悬殊,拟合最终残余下沉值也不一样。可以看出,若对工作面停采后的实测数据拟合,由于该时间段前期数据反映了岩体变形破坏及过渡阶段的地表沉陷,下沉速度衰减过快,拟合的负指数函数参数b值明显过大,而实际上地表残余下沉衰减很慢。显然,公式(4)作为该矿长壁综放开采地表残余下沉系数的计算公式更为准确。

表2 工作面停采后110号测点累计下沉量实测数据与预计结果比较
4结论
(1)采用数值模拟方法分析了地表沉陷由岩体变形破坏到岩体密实沉陷的发展过程,揭示了岩体密实沉陷延续是引起地表残余沉陷变形的机理。
(2)通过综合分析,确定了长壁开采条件下地表残余沉陷变形概率积分法预计参数的计算方法和取值范围,对采空区的稳定性评估有一定的参考价值。
[参考文献]
[1]滕永海,张俊英.老采空区地基稳定性评价[J].煤炭学报,1997(5):58-62.
[2]邓喀中,谭志祥,张宏贞,等.长壁老采空区残余沉降计算方法研究[J].煤炭学报,2012,37(10):1601-1605.
[3]朱广轶,解陈,窦明,等.老采区及地表残余变形对建筑物的影响[J].沈阳大学学报(自然科学版),2012(3):70-74.
[4]何国清,杨伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991.
[5]北京开采所.煤矿地表移动与覆岩破坏规律及其应用[M].北京:煤炭工业出版社,1982.
[6]戴华阳,王金庄.非充分开采地表移动预计模型[J].煤炭学报,2003,28(6):583-587.
[7]黄乐亭,王金庄.地表动态沉陷变形的三个阶段与变形速度的研究[J].煤炭学报,2006,31(4):420-424.
[8]张俊英.采空区地表新建建筑地基稳定性与治理技术研究[D].徐州:中国矿业大学,2005.
[9]国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M].北京:煤炭工业出版社, 2000.
[10]刘晓菲,邓喀中,范洪冬,等.D-InSAR监测老采空区残余变形的试验[J].煤炭学报,2014,39(3):467-472.
[11]郭广礼,邓喀中,谭志祥,等.深部老采区残余沉降预计方法及其应用[J].辽宁工程技术大学学报(自然科学版),2002,21(1):1-3.
[12]王明立,张华兴.采煤沉陷区地表残余移动变形的计算分析[A].2005年开采沉陷规律与三下采煤学术会议[C].2005.
[责任编辑:施红霞]
Forecast Parameters and Numerical Simulation of Mechanism of Surface Residual Subsidence Deformation
YI Si-hai
(CCTEG Tangshan Research Institute,Tangshan 063012,China)
Abstract:Overburden strata movement process was studied by numerical simulation,the results showed that surface subsidence experienced the process that from rock mass deformation to rock mass subsidence,it revealed that rock mass subsidence development was reasons that induced surface residual subsidence deformation. Surface residual deformation could be predicted by probability integral method according numerical simulation of surface subsidence distribution law during rock mass subsidence stage.On the basis of numerical simulation and measured data,predicting parameters of probability integral method of surface residual subsidence deformation with long wall mining situation were confirmed.
Key words:residual subsidence deformation; numerical simulation; subsidence process; predicting parameters; long wall mining
[收稿日期]2015-08-19
[基金项目]国家自然科学基金项目(51474129)
[作者简介]易四海(1980-),男,湖北公安人,副研究员,博士,主要从事开采沉陷规律与“三下”采煤方面的研究工作。
[中图分类号]TD325
[文献标识码]A
[文章编号]1006-6225(2016)02-0029-04
[DOI]10.13532/j.cnki.cn11-3677/td.2016.02.009
[引用格式]易四海.地表残余沉陷变形机理数值模拟与预计参数分析[J].煤矿开采,2016,21(2):29-32.
