加载速率对SAC系列焊点蠕变性能影响的研究

范海平　刘海涛

【摘 要】随着微电子封装技术的不断发展，焊点的形式以及焊点所用无铅钎料的种类愈发繁多，从而使得对焊点力学性能的考察尤为重要。在所有对焊点性能的考察中抗蠕变性能是一项重要的考察项目，本篇文章通过实验和有限元数值模拟两种方法加载速率对焊点抗蠕变性能的影响。对SAC系列钎料焊点进行纳米压痕实验及模拟，获得载荷-深度曲线、时间-深度曲线，以及时间-蠕变速率曲线。结果表明：蠕变的速率并不是恒定的，随着加载速率的增大，钎料的蠕变程度以及蠕变速率依次增大，并逐渐减小，最终趋近于零。

【关键词】蠕变；纳米压痕；有限元模拟；焊点；加载速率

0 序言

电子器件服役时，相对于服役的环境温度，焊料自身熔点较低，随着时间的延续，产生明显的焊点蠕变损伤。由于蠕变性能对于高温材料的使用至关重要，是影响焊点失效行为及焊点可靠性的重要因素。因此，研究材料的蠕变性能是微电子封装焊接研究中一个重要的部分[1-3]。

但在实际测量中，对于微电子封装焊点这类本身体积很小的测量件，由于钎料属于软金属，并且在加工钎焊后会产生明显的尺寸效应，各种性能受尺寸的影响明显不同于传统焊接。所以对于微电子封装焊点只能通过纳米压痕蠕变来获得其蠕变性能参数。

在过往研究中，已有过研究剪切力大小、饱载时间、加载方式对焊点蠕变性能的影响；而本文借助纳米压痕仪及先进的有限元计算机模拟软件对SAC系列钎料（Sn-3Ag-0.5Cu，Sn-0.3Ag-0.7Cu， Sn-0.3Ag-0.7Cu-0.07La）焊点进行一次加载-卸载纳米压痕实验、模拟，得到载荷-深度曲线 （load-depth曲线），通过对实验数据的分析获得焊点蠕变程度及蠕变速率在加载速率影响下的变化规律。

1 纳米压痕及有限元分析理论

1.1 纳米压痕法

纳米压痕法主要通过测量加载、卸载过程中压头作用力与载荷深度得到的加卸载曲线来获得样品的硬度与弹性模量等力学性能参数。进行纳米压痕测试时压头需垂直于样品被压面，等压头接触试样表面后开始加载，直至加载到最大值后再缓慢卸载，实时检测压头压入位移随载荷的变化。测试的结果是一组载荷-位移曲线，通过对load-depth曲线进行物理反解析计算能获得材料的弹性模量、硬度及蠕变应变速率敏感指数等力学性能参数。

一般来说，纳米压痕仪用于测量硬度H和弹性模量E是两个钎料的基本力学参数，它们对于研究一种钎料的力学性能起到了很重要的作用。纳米压痕法测量材料的H和E的基本公式为：

式中：ε取决于压头几何形状，三棱锥压头ε=3/4；hr是由力-位移曲线中的最大应力点Fmax沿着卸载曲线开始向下引切线，与横坐标轴的交点。

本实验利用纳米压痕仪中队压痕位移深度的精确测量及纳米压痕技术中所采用的计算公式（式3）来分析焊点在受压后保载时间内发生的蠕变。

图1为一条典型的纳米压痕测量出来的材料蠕变特征的loading-depth曲线，最大载荷处停留的一段时间内所产生的压入深度h与时间t的关系曲线反映了该材料的蠕变特征。

1.2 有限元模拟技术

有限元的基本原理是将求解未知场变量的连续介质体划分为有限个单元，单元用节点连接，每个单元内用插值函数表示场变量，插值函数由节点值确定，单元之间的作用由节点传递，建立物理方程。将全部单元的插值函数集合成整体场变量的方程组，然后进行数值计算。数值分析在对理解材料在微纳米尺度或微纳米表层的力学性能的问题中体现出了突出的优势[4]。

所以现在国内外对封装体系热应力与机械应力失效的分析和预测，主要采用有限元分析方法[5-7]。有限元方法已经成为求解实际工程问题的一种重要手段，并且逐步开发相应的有限元软件，如ANSYS、MARC和ABAQUS等，具有处理几何非线性、材料非线性和包括接触非线性在内的边界条件非线性以及组合的高度非线性的超强能力；可以处理各种结构的静力学、动力学（包括模态分析、瞬态响应分析、简谐响应分析、谐响应分析）问题、温度场分析以及其他多物理场耦合问题；同时拥有高数值稳定性、高精度和快速收敛的高度非线性问题求解技术。

2 研究步骤

2.1 实验

（1）采用感应加热的方法，制备出Sn-3Ag-0.5Cu，Sn-0.3Ag-0.7Cu， Sn-0.3Ag-0.7Cu-0.07La三种钎料。

（2）采用装有丙三醇的电炉坩埚，加热到280°C制备直径为900μm的BGA焊球。

（3）将超声波清洗后的焊球在助焊剂的作用下回流焊接在铜基板上，形成回流BGA焊点。

（4）将回流BGA焊点依次使用80#、600#、1200#、2000#砂纸在低速金相抛光机上进行打磨及抛光，直至露出焊点，并保证焊点截面处无划痕，获得金相压痕试样如图2

（5）利用纳米压痕仪采用一次加载-卸载方式并配有多种加载速率对三种钎料制成的焊点进行蠕变性能测试，来研究加载速率对焊点蠕变性能的影响。

2.2 模拟

三维模型的自由度高于二维的一个数量级以上，这将导致三维模型中积累的数据误差对模拟的结果存在很大的影响[8]；其次，三维中模拟结果可能与网格的划分存在很大相关性[9]。

为了简化分析，在模拟时压针被简化为顶角半角α=70.3°的圆锥刚体，因此横截面面积和深度的比例与Berkovich压针和Vickers压针是相同的。为了获得更好的模拟结果，本模拟中模型的尺寸均采用实验样品的真实大小，利用二维有限元模型模拟BGA单个焊点组件的几何尺寸为压头（金刚石）：半径0.037mm，高度0.015mm；PCB基板（FR4）：1.27×1.27×0.36mm；焊盘（Cu）：直径0.86mm，高度0.025mm；IMC（Cu6Sn5）：直径0.54mm，高度0.002mm；焊点（Sn3.0Ag0.5Cu）：直径0.9mm，高度0.72mm，各组件的物理参数如表1所示。

在纳米压痕实验的基础上，利用反分析测试原理并结合数值模拟方法，建立了微小无铅焊点压痕实验中载荷-位移关系曲线与其弹塑性材料参数之间的联系，并以幂指数本构方程的形式表征Sn3.0Ag0.5Cu无铅钎料的的塑性性能[10]，如式（4）所示。

为了简化造型及缩短模拟时间，可考虑模型为x轴对称结构，取模型1/2进行分析，同时忽略了摩擦的影响，认为各组件工艺质量良好无缺陷，焊点在整个分析过程中受到均匀的载荷，并对组件的初始状态做理想处理（无应力状态）。建立的BGA单个焊点的二维模型如图3所示。

3 实验结果及分析

本次研究采用一次加载-卸载的方式，最大载荷为200mN；加载速度分别为5mN/s，10mN/s，20mN/s，50mN/s；在最大载荷处保载180s。压痕测试过程中，为了避免相邻的两个压痕应力场的相互影响而导致数据准确度下降，即为了避免边界效应，相邻压痕之间需保持3倍于压痕尺寸大小距离 [11]，如图4。

3.1 蠕变过程分析

选取Sn-0.3Ag-0.7Cu-0.07La/Cu焊点进行压痕试验后得实验数据进行分析，在最大载荷为200mN，保载时间为180s，加载间隔为0.15s的实验条件下，利用Origin软件绘制在保载时间内，三种焊点在5mN/s的加载速度下的蠕变加速度变化情况，如图5所示。

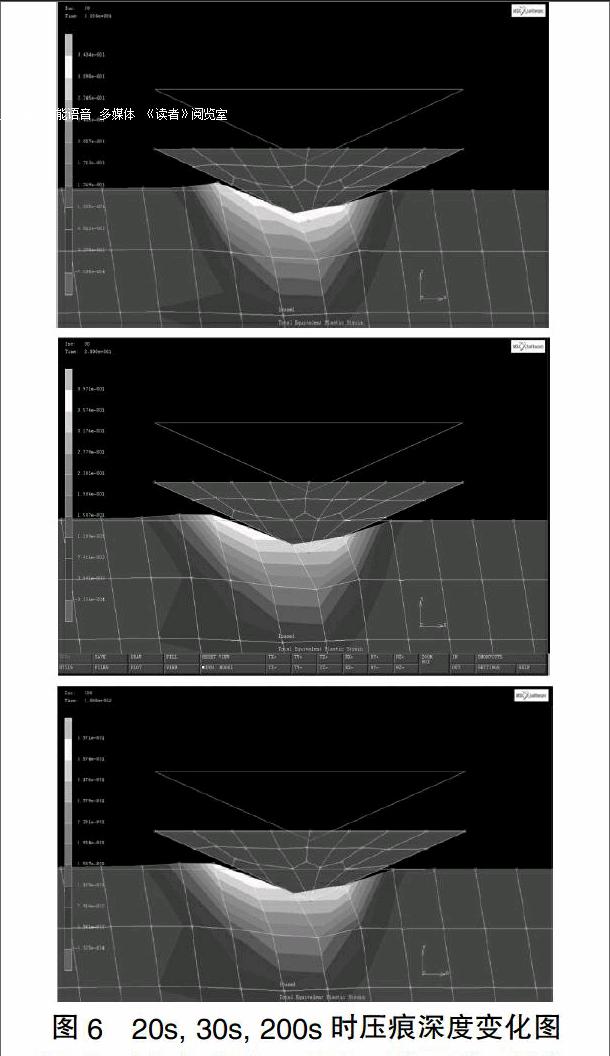
对利用有限元软件建立的SAC305焊点模型进行同一实验参数的模拟，同样采用一次加载-卸载的方式，最大载荷为200mN；加载速度为5mN/s，在最大载荷处保载180s。可以清晰的看出在保载时间内压痕深度随着时间的延长不断加深，即产生了较为明显的蠕变，如图6。再通过对模拟结果进行逆向分析可得在模拟条件下的SAC305焊点压痕蠕变速率-速度曲线，如图7。

由图5及图7可知，在保载时长内，蠕变速度在蠕变发生时达到最大，经过一个较短时间，蠕变速度便趋向于0，之后很长的一段时间内，蠕变速度无限接近于0，这表明钎料蠕变速度最大点发生在其刚产生蠕变时，之后蠕变趋近于不在发生，即速度接近于0。同样，可发现在10mN/s、20mN/s、50mN/s也有相同的规律。这一现象表明了钎料的蠕变过程是一个明显的变速过程。这是由于钎料焊点在不同应力载荷的作用下将会发生蠕变激活过程，导致位错滑移和攀移，以及晶界滑移的速率不同，这个过程同时伴随着热扩散过程的不均匀性，最终导致钎料焊点蠕变速度在不同应力载荷下产生不同的的蠕变速度且这个过程是不匀速的。

3.2 蠕变量分析

在这部分，实验过程中选取三类焊点分别在5mN/s，10mN/s，20mN/s和50mN/s的加载速度下的蠕变深度变化数据，利用Origin软件绘制出钎料蠕变深度与时间的关系曲线图，采用S曲线拟合，所得出的曲线如图8所示。

以相同的参数添加入之前所建立的有限元焊点模型，在相同的加载条件下进行数值模拟。同上一节一样对所得到的数据值进行选取、采集。在此基础上利用作图软件进行绘图。获得载荷-蠕变量曲线如图9。

由图中8可以直观的看出，焊点所受加载速率越大则蠕变量的最大值越高。而从有限元模型（图9）可以发现越高的加载速率实验值所产生的蠕变量越大，即从图上所表现出来的当载荷达到最大值并保载过程中，蠕变量所形成的的平行于x轴的横线长度随着加载速率的增大而由短变长。这表明钎料的蠕变变形量随着加载速度的增加而呈现非线性加大的趋势，焊点的蠕变程度与加载速度有关，随着加载速率的增大，钎料的蠕变深度也依次增加。

这是由于加载速率越大，达到最大载荷的时间越短，材料依赖时间的变形就越小，则积累的塑性变形能就越大，在饱载弹性能释放，转变为较大的蠕变变形量[9]。

3.3 蠕变速率分析

根据试验过程中SAC系列三种焊点在5mN/s，10mN/s，20mN/s，50mN/s四种加载速率下获取的数据，利用所学Origin绘图软件绘制出四种加载速度条件下钎料焊点的时间-蠕变速度变化曲线图，如下图10所示（注：图10为从保载开始后的时间-蠕变速率曲线）。

采用相同的数据，利用有限元模型模拟上述实验。可直接提取出压痕模拟中四种不同加载速率条件下的时间—蠕变速率曲线如图11（注：图11也是为从保载开始后的时间-蠕变速率曲线）。

由实验所获得的图10可以看出，在5mN/s，10mN/s，20mN/s，50mN/s四种加载速度下，三种钎料焊点的蠕变最大速度都发生钎料刚产生蠕变时，逐步的降低，最终的蠕变速度无线接近于0。在放大截图的任意时间点处，做一条垂直于x轴的竖线，可以看出加载速率越高所对应的曲线所处的点越高。又如图11所示，虽然在理想条件下受到明显的加载时间及保载时间的影响，未能出现明显的如图10所示任意时间点上加载速率越大，对应此时的蠕变速率越大的现象，但将四种加载速率当加载过程结束，进入保载过程后可以明显的看到50mN/s的蠕变速率值最高，其次为20mN/s、10mN/s。蠕变速率值最小的是5mN/s。由此我们可以分析出钎料的蠕变速率也在很大程度上受加载速率的影响，表现为蠕变速率随着加载速度的增大而增大的规律。

这一现象可从蠕变的两种机理[12]进行分析，首先由扩散蠕变机理分析可得，加载过程中，加载速率大，则对于焊点所受的初始载荷就大。蠕变的产生是由于材料内部的空位浓度差而产生的；并且空位浓度的变化量与材料的外加应力成正比。当加载速率增大时，对于焊点即可视为外加应力的增大，在较大的应力的作用下使得钎料焊点内的空位进行了快速移动，由此即产生较大的空位差，促进了蠕变的进行，即表现为蠕变速率随着加载速率的增大而产生明显的上升趋势。

其次由晶界滑移机理分析可得，因为当材料中不存在液相时，蠕变速率与应力的平方成正比，并且晶界旁边的位错变形支配整个过程。较大的加载速率给予了晶界较大的初始应力，较大的外加载荷可以激活了较多的晶界进行滑移，而较多的晶界滑移更加促进了蠕变的产生，提高了蠕变的速率。

4 结论

通过实验和数值模拟这两种方法的对照分析，我们获得了如下结论：

（1）三种钎料焊点在恒定载荷下的蠕变深度-时间关系图体现了钎料焊点的蠕变变化速率特性，即在某一恒定载荷速率下，蠕变速率变化在蠕变刚发生时最大，在保载阶段内，蠕变速率逐渐减小，最终无限接近于0，说明钎料焊点的蠕变过程不是一个匀变过程，而是一个变速的过程。钎料蠕变变形发生在载荷最大处，并在保载阶段愈加明显。

（2）BGA焊点在纳米压痕试验中加载速率越大，蠕变量越大，即钎料的蠕变程度表现出明显的加载速率相关性。不同加载速度下在进入饱载时间点前后，钎料蠕变速率变化受到加载速度的影响较为明显，焊点处的蠕变速率随加载速度的增大而呈现出增大的趋势。

（3）在通过对比了蠕变加载速率与加载时间的关系曲线后，发现实验结果与数值模拟有较好的符合性。模拟作为一种新型的工程工具，完全可应用于实验、生产前的可实时性及结果的预判。对实验及生产具有着巨大的指导意义。

【参考文献】

[1]王飞，徐可为.加载速率对Al膜纳米压人蠕变性能的影响[J].金属学报，2004，40（11）：1138-1142.

[2]姬峰，薛松柏，刘霜，娄继源.纳米压痕法测量锌铝钎料的室温蠕变应力指数[J].焊接学报，2013，34（2）：75-78.

[3]YAN Yanfu， YAN Hongxing， CHEN Fuxiao， ZHANG Keke， et al. Influence of stress on the creep behavior of Cu particle enhancement Sn-Pb based composite solder joints [J]. RARE METALS， 2007，26（1）：51-55.

[4]LI Min， LIANG Nai-gang， ZHANG Taihua， WANG Lindong et al. Nanoindentation dimensional finite element numerical test[J]. Mechanics， 2003 （5）：257-260.

[5]David Followell， Salvtore L Ligurore， Rigo Perze， et al. Computer-aided reliability finite element methods[J]. the IES，1991，（9-10）：46-52.

[6]M Mukai，T Kawakami，Y Hiurta，etc. Fatigue life estimation of solder joints in SMT-PGA Packages [J]. Elec. Pack，1998，120（6）：207-212.

[7]N Paydar，Y Tong，H U Akay. A finite element study of factors affecting fatigue life of solder joints [J]. Elec. Pack，1994，116（12）：26-273.

[8]Ricky Lee S.W.， Huang X.J. Analysis on solder ball shear testing conditions with a simple computational model[J]. Soldering &Surface Mount Technology， 2002，4（1）：45-48.

[9]Lai Y.S.， Kao C.L.Characteristics of current crowding in flip-chip solder bumps [J]. Microelectronics Reliability，2006， 46（5-6）：915-922.

[10]Zhu Fulong， Song Shao， Zhang Wei et al. Creep behavior investigation of lead-free solder. Association for Computing Machinery， 2010，195-198 alloy n96.5Ag3Cu0.5[C].

[11]王丽凤，戴洪斌.微焊点纳米压痕循环力学行为与承受载荷的关联性[J].焊接学报，2013，34（10）：75-78.

[12]王要利.RE对低银Sn-Ag-Cu焊点蠕变及时效特性的影响[M].河南科技大学，2007：6-7.

[责任编辑：汤静]