提高高中学生数学直觉能力的探索

◎陈海兵

提高高中学生数学直觉能力的探索

◎陈海兵

本文分析了数学直觉在数学学习和数学发现中所起的作用，提出培养学生数学直觉能力的必要性，然后从培养学生对数学美的鉴赏能力，鼓励学生积极猜想，丰富学生想象力；培养学生良好的反思习惯及概括能力这三个方面阐述了如何培养和提高学生的数学直觉能力。

数学直觉；高中学生；探索

数学直觉是数学研究中的非逻辑成分。徐利治教授的《数学直觉的意义及作用》一文中明确写道：“数学直觉是可以后天培养的。实际上，每个人的数学直觉也是不断提高的。”这也说明，教师在传授知识的过程中是可以把数学直觉传授给学生的。那么，在数学教学过程中，我们应该如何培养学生的数学直觉呢？笔者结合自己的教学实践谈一些做法。

一、培养学生对数学美的鉴赏能力

英国著名哲学家、数理逻辑学家罗素曾把数学的美形容为一种“冷而严肃的美”。他在《我的哲学的发展》一书中写道：“数学，如果正确地看它，它不但拥有真理，而且也具有至高的美，正像雕刻的美，是一种冷而严肃的美，这种美不是投合我们天性的微弱的方面，这种美没有绘画或音乐那些华丽的装饰，它可以纯净到崇高的地步，能够达到严格的只有最伟大的艺术才能显示的那种完美的境地。”可见，只有懂得数学美的人才会用心在数学能力的培养上，努力提高自身的数学修养，让产生数学直觉成为可能。

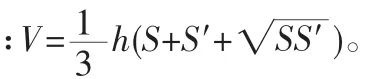
二、鼓励学生积极猜想

数学猜想实质是一种数学想象。想象可以进行创造性的综合，以形象的方式来改造旧的经验，提出新的假说或新的模型。爱因斯坦甚至认为“想象力比知识更重要……是科学研究中的实在因素。”普朗克在谈到自己的科学创造体会时指出：“即使是严格的科学研究，没有想象力自由发挥，也不能前进。”可见，人们把想象誉为思维的翅膀是不无道理的。我们的学生很小就在进行形如11，14，19，26，35，()这样的数列中项的猜想训练，我们不能因为学生学了数列的通项公式，而放弃基本的猜想训练。公务员行政职业能力测试里的数字推理和图像推理的题目，很好地考查了数学直觉，考生必须具有一定的猜想归纳能力才可能顺利完成这些题目。为了培养学生的想象力，在教学过程中教师必须鼓励学生大胆猜想解题过程、答案，还要鼓励学生猜定理、公式，想象未知对象的各种图像或模型。如果学生猜错了，那要鼓励学生寻找错误的原因，不能打击学生，否则就会扼杀学生的数学直觉能力。

三、培养学生良好的反思习惯及概括能力

赵振威教授在《数学解题后的再发现》中指出：“为了更好地拓宽解题思路，积累解题经验，提高解题效果，在解答数学题后，应当有目的地进行再发现。”

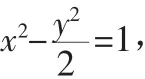
解法分析：首先，我们假设这条直线是存在的，由题意可知直线若存在，直线的斜率也是存在的，通过点差法求出直线的斜率为2。到此，几乎所有的学生都写出了直线方程，没有人去想，满足题意的直线事实上是不存在的，在求斜率的值的过程中产生了增根。无论是通过作图或是联立求判别式检验都是很简单的过程，而学生缺的只是检验的思想。

逻辑和直觉各有其必要的作用，两者缺一不可。唯有逻辑能给我们可靠性，它是证明的工具；而直觉则是发明的工具，它使我们具有一览遥远目标的本领。因此，我们既应加强逻辑思维的训练，提高抽象思维能力，又要注意培养数学直觉能力，提高创造能力。

(作者单位：浙江省平阳县鳌江中学325400)

G633.6

A

1992-7711(2016)11-0035