需求信息不对称下存在直销模式的产能管理研究

谢文明，江志斌，储熠冰，王康周



需求信息不对称下存在直销模式的产能管理研究

谢文明1,2，江志斌1,2，储熠冰1,2，王康周1,2

(1.上海交通大学中美物流研究院，上海200030；2.上海交通大学机械与动力工程学院工业工程与物流系，上海200240)

研究了如何保证可靠的预测信息在供应商和分销商组成的供应链中进行共享的问题。为了改善传统供应链绩效，将直销市场引入供应链。为解决多销售渠道的能力计划与分配问题，提出了两阶段决策制定机制，并证明了最优解属性。信息更新前，供应商设计了产能预定合同，通过提前预定产能激励具有信息优势的分销商向供应商传递真实的市场需求信息；信息更新后，为实现利润最大化，供应商重新设计了四种产能分配策略。最后，对各种决策模型进行了计算和仿真，验证了信息不对称条件下带有直销市场的两阶段决策机制的有效性。

信息不对称；信息更新；直销市场；机制设计

0 引言

在服务型制造环境下，供应链不只提供产品，而且提供基于产品的服务[1]。由供应商、分销商及客户组成的供应链中，供应商提供主要的产品和服务，分销商在供应商提供的基本产品和服务的基础上为顾客提供附加的服务。供应商可以选择通过分销商销售产品或服务也可以选择直接销售给客户。在紧固件行业中，存在几万种产品规格，每个紧固件供应商提供的产品规格不超过1000种。为满足顾客需求，分销商则从多家紧固件供应商采购，确保可以满足客户企业的紧固件产品需求[2]。基于成本的考虑，存在多产品需求的顾客往往选择从分销商购买，需求相对单一的顾客往往选择直接从供应商购买。因此，供应商拥有两个销售渠道：直接销售给顾客和通过分销商销售给顾客。随着网络经济的发展，很多企业纷纷投入相当多的资源，开始进行网络直销。当一个企业同时运用包括直销和分销渠道在内的多个销售渠道满足顾客需求时，即为多渠道供应链管理。直销模式的兴起使得供应链从单一销售渠道向分销与直销混合并存的多渠道方向发展。比如，联想是通过分销模式向直销和分销相结合的模式发展，而戴尔是通过成功的直销模式向直销与分销相结合的模式发展，二者殊途同归。对很多企业来说，直销渠道有很多传统分销渠道无法比拟的优势，比如，能更好地控制价格、能够为顾客提供更多的产品选择和更好的服务、更易于收集顾客信息以及更有利与供应商与分销商进行谈判等。然而，传统渠道中的分销商由于更接近顾客可以通过培训、广告、收集市场信息、订单跟踪以及品牌建设等措施有效地创造和维持顾客。因此，同时使用分销和直销渠道将比单一渠道更具竞争优势。Clay等（2000）[3]认为企业应该有效发挥两种渠道之间的互补性，而不是替代性。在许多销售过程中，分销渠道与直销渠道往往可以同时发展。因此，有效地设计和运用多渠道销售模式可以增强企业的综合竞争力，给企业带来更多利润。

供应链本质上是由相互独立的决策主体构成的分布式系统，各决策主体一般根据其所掌握的信息做出相应的决策，因此共享精确的信息无疑是提高供应链运作效率的关键，然而信息不对称却普遍存在于供应链的运作过程中。在分散化决策的供应链（decentralized supply chain）中，由于分销商本身具有营销专长并且更接近客户群体，分销商往往会获得更多关于市场的私有信息[3]。为了更好的规划产能，供应商希望分销商进行最大程度的需求信息共享，例如促销和需求预测。然而，为了避免产能不足导致损失，分销商往往会夸大需求。考虑到牛鞭效应，供应商不会完全相信分销商提供的需求信息。缺乏可靠的预测信息，必然会导致产能不足或产能过剩并造成双方的收益损失。因此，为了合理进行产能计划，供应商需要建立有效的合同机制激励销商提供更可靠的需求信息。当产能规划完成后，需求信息被更新，供应商要重新考虑分销商与直销市场的产能分配。这时，供应商更倾向于满足直销市场，因为直销市场的价格普遍高于给分销商的批发价格。因此供应商的产能决策制定过程需要考虑不对称信息、双重边际化效应以及需求信息更新后的产能再分配。

本文研究了信息不对称条件下供应链信息共享和信息更新、产能分配的问题。Aviv(2003)对信息预测问题进行了综述[4]。Cachon(2004)[5]和Erkoc等[6](2005)提出了对称信息条件下提前采购合同、产能预定合同可以将产能过剩风险从供应商转移给下游的结论。Erhun（2003）考虑了采购顺序和重复采购对供应商产能的影响[7]。上述文献都是建立在所有信息均为已知且对称的基础之上。Lau等(2001)通过报童模型阐述了预测信息不对称问题导致的影响[8]，但并未提出有效的机制甄别可靠的预测信息。索寒生等（2004）研究了回购决策可以实现信息共享[9]。唐宏祥等（2004）研究发现零售商可以通过采购价格向供应商传递真实可靠的市场需求信息[10]。Iyer等[11](1997)、Fisher等[12](1996)、Ozerl[13](2003)、Barnes-Schuster等[14](2002)研究了销售季节之间供应链预测信息更新问题。Barnes-Schuster等(2002)提出了在对称信息条件下应用期权合同解决多周期信息更新协调问题[14]。从信息经济学的微观角度研究信息共享的文献中，Puettmann等(2010)提出了与本文相似的问题。所不同的是，作者提出的联合计划机制是基于双方多次合作的基础上[15]。

基于供应链上下游需求预测和信息共享，以信息经济学和最优化理论为工具，提出并解决了信息不对称条件下产能计划与分配问题。本文的贡献体现在如下两点：第一，以最小化供应链效率损失为目标，提出了协调多销售渠道供应链的产能预定合同。第二，分析了四种预测需求信息与更新需求信息偏离的情景，提出了灵活的参数调整策略。

1 问题描述

考虑由一个供应商和一个分销商组成的两级供应链，供应商作为主要产品和服务的提供商，需要做出两个决策：总产能计划和分销商、直销市场的产能分配决策。作为拥有私有预测信息的分销商，为了最大化自身收益，需要决定多大程度共享私有需求信息。决策制定过程包括两个阶段：合同设计阶段和合同参数优化阶段。首先供应商向分销商提供合同菜单（分配产能、产能预定支付），供应商根据分销商选择的最优合同确定最优产能。在第二阶段，供应商建立最优产能后，需求信息被更新，供应商调整合同的参数，重新分配产能和确定支付。然而，供应商在第二阶段的产能最优分配决策可能与第一阶段的分配决策冲突。因此需要根据更新需求调整供应商和分销商之间补偿支付，确保分销商获得不低于第一阶段的收益。

1.1假设与参数

如上所述，在第一阶段，供应商通过合同设计确定最终产能计划。在第二阶段，需求信息更新后，通过合同参数再优化，重新确定产能分配和补偿支付。不失一般性，本文采用如下假设：

假设1. 供应商的产能计划与分配是单周期决策问题。供应商可以建立任意数量的产能。分销商不能建立产能，也就是说分销商只能向供应商采购产品与服务。

假设2. 供应链中只存在三个参与方：供应商、分销商和直销市场，且直销市场和分销商的客户需求无关联。所有成本和价格均为外生给定。直销市场的价格要远高于分销商的批发价格。

本文参数如表1所列。

表1 参数符号

1.2模型

供应商利润、分销利润及供应链利润可以被表示为，

（2）

（3）

1.2.1信息对称条件下的集中化供应链

在集中决策化供应链（centralized supply chain）中，分销商的私有信息是共同知识。对称信息条件下，当分销商和供应商进行完全合作，供应商获得整个渠道的全部利润，

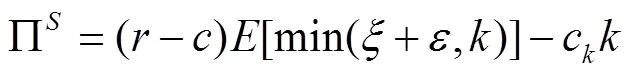
（5）

1.2.2信息对称条件下的分散化供应链

分散化供应链条件下，分销商和供应商的目标为最大化各自的利润。供应商可以获得分销商精确的私有预测信息，并且分配所有产能给分销商。此时供应商的利润表示为，

（7）

1.2.3 信息不对称分散化供应链

当供应商不能获得分销商私有预测信息时，为了确保客户需求被满足，分销商总会提给供应商供夸大的需求信息（牛鞭效应）。此时分销商的预测需求信息，包含两个随机变量、。最大化（6），可以得到对称信息条件下最优产能，

2 基于产能计划和分配的决策制定机制

本文聚焦在供应商产能计划和分配问题上，通过以下两个阶段进行描述：

阶段2：产能再分配阶段。所有需求信息在这个阶段被更新。因此，根据已建立的总产能、分销商的更新需求和直销市场的更新需求，供应商优化最优产能预定支付和分配比例。

2.1 供应商产能计划阶段

（10）

（11）

供应商的主要问题是通过设计合同菜单引导出真实预测信息以实现利润最大的目标。由显示原理[19]得知，贝叶斯博弈的任何贝叶斯纳什均衡，都可以重新表示为一个激励相容的直接机制。在这种合同机制中，分销商显示了自己的真实信息才可以最大化利润。因此，供应商需要求解问题：

第一个约束集为激励相容约束(IC)，第二个约束为参与约束(PC)。IC激励分销商向供应商显示他的真实信息，PC保证分销商可以获得不低于其保留收益的利润，从而激励分销商参与合同。此外，和反应了需求信息的上下限。

由显示原理，定义分销商的最优利润和供应商的最优利润为，

证明：因为

分销商的最优利润

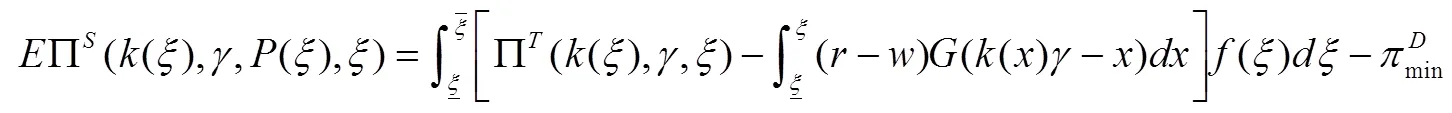
对其进行分步积分得，上式的最大化问题可以表示为，

（15）

（16）

（17）

正态分布、均匀分布或指数分布均满足风险率为增函数条件。当分布函数为幂函数，且次数大于等于一时，概率密度函数为增函数条件也满足。然而这两个条件只是最优解的充分而非必要条件。

2.2 供应商产能分配

尽管存在大量关于供应链产能计划和分配的研究，但大多数优化模型主要是基于静态而非动态的决策。然而，当需求预测存在明显错误，基于静态的决策效率将显著降低。

上述问题可以详细表述为，

（21）

图1 产能重分配的四种类型

此时（21）可以被重新写为，

当产能过剩时，供应商可以满足分销商和直销市场的需求。由于分销商预测失误，分销商在第一阶段的预定产能小于实际需求，供应商可以增加对分销商的销售而收取超出预定产能部分的支付。供应商设定产能分配比例满足分销商和直销市场的全部需求。此时供应商的利润为，

简单起见，设定额外产能支付和预定产能支付之比等于额外产能与预定产能之比：

在类型1中，供应商和分销商的利润可以表示为，

当产能不足时，供应商将不能满足分销商和直销市场的总需求。因为直销市场的价格要高于给分销商的批发价，因此供应商选择优先满足直销市场的需求。供应商通过设定产能分配比例优先满足直销市场的需求。此时供应商的利润为，

在产能不足的情况下，供应商优先满足直销市场，将导致分销商不能满足客户的需求。因此，供应商需要补偿分销商以确保分销商可以获得预定产能下的利润。这意味着，其中反映了供应商对分销商因为产能短缺导致客户损失的部分补偿。因为分销商也存在预测失误，所以由分销商自己提供剩下部分的客户损失补偿。此时对应的分销商的支付为，

因此，在类型2条件下，供应商和分销商的利润可以表示为，

此时（21）可以被重新写为，

讨论过程与类型1相似。当存产能过剩时，供应商的产能可以满足分销商和直销市场的总需求。供应商通过设定产能分配比例满足分销商和直销市场的全部需求。此时供应商的利润为，

由于预测失误，分销商更新的需求低于预定产能。因此，分销商要独自承担这部分损失，分销商对预定产能的支付不会降低，即。

在类型3中，供应商和分销商的利润可以表示为，

讨论过程与类型2相似。当产能不足时，供应商将不能满足分销商和直销市场的总需求。供应商通过设定产能分配比例优先满足直销市场的需求，用剩余产能满足分销商的需求。此时供应商的利润为，

在产能不足的情况下，供应商优先满足直销市场，将导致不能满足分销商的更新需求。因此，供应商需要补偿分销商以确保分销商可以获得更新需求下的利润。这意味着，其中反映了供应商因为产能短缺导致客户损失的补偿。因为分销商的预定产能超出了更新需求，而供应商没能满足分销商的更新需求，因此对分销商客户的补偿由供应商全部承担，即。同时假设对客户未满足需求部分的补偿与类型2的补偿比例一致。此时分销商的支付为，

因此，在类型4条件下，供应商和分销商的利润可以表示为，

通过上述分析，得到图2所示的合同参数的变化情况。

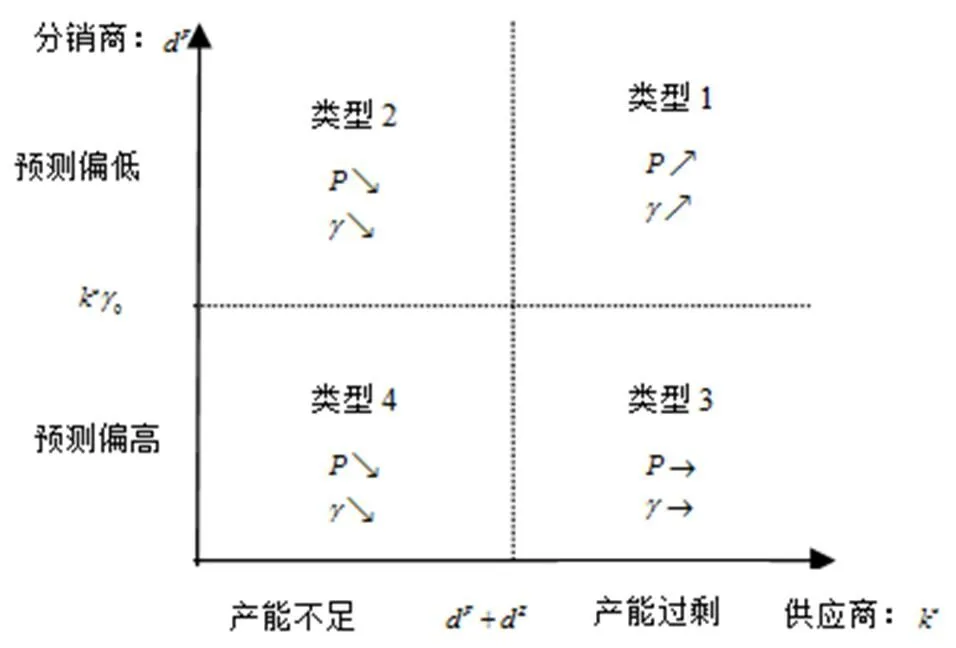
图2 产能重分配的四种类型解

供应商作为供应链的主导者，通过调整合同参数最大化利润。通过引入直销市场，供应商既可以扩大市场份额又能降低产能过剩的风险。公平起见，本文假设每一方都要为各自行为导致的损失负责。因此，分销商会为了减小损失而努力提高预测的精度。此外，通过产能的再分配和最优解的调整可以促成责权清晰的供应链伙伴关系：供应商负责合理地规划产能，分销商负责提供及时精确地市场信息和预测报告。

3 算例分析

3.1 不同合作模式下绩效分析

本文采用类似文献[16]的参数设置模式，假设所有的成本和价格均为外生给定。在信息不对称分散化供应链条件下，市场的不确定系数服从-5到5的均匀分布，零售商的需求信息服从10到20的均匀分布，直销市场的需求服从0到10的均匀分布。根据2.2节计算集中化决策下及批发价格合同下的最优产能、能力分配系数及利润，根据3.1节定理2可以计算得出能力预定合同下最优产能、能力分配系数及利润。为了比较私有信息对最优决策的影响进而验证文中的定理，表2给出了低私有信息及高私有信息条件下，最优产能数量、分配比例、供应商利润、分销商利润及供应链总利润。

表2 不同合作模式下决策和利润的比较

从表2可以得出结论：第一、由于不存在信息不对称及双重边际效应的影响，集中化决策下的供应链总利润高于批发价格合同及能力预定合同下的供应链总利润。第二、相对于批发价格合同，制造商通过能力预定合同协调了零售商的决策，增加了制造商利润和供应链的总利润。此时，制造商目标为最大化总剩余及提取代理人信息租金之间的权衡。由于信息租金是分销商私有信息的增函数，因此为了降低类信息租金，制造商将会向下扭曲产能，导致了代理损失。第三、批发价格合同下，由于制造商的能力设置不是私有信息的函数，因此批发价格合同下制造商将会设置独立于私有信息的常数生产能力。然而，在能力预定合同下，制造商的能力设置是零售商私有信息的函数，并且制造商的最优能力将随着私有信息的增加而增加。第四、在高私有信息条件下，供应商的能力决策随着私有信息的增加而更接近集中化决策数量。当私有信息由12增加到18，与集中化决策解的差距由4.48(19.60-15.12)降低到2.12(28.15-26.03)。这一结果说明制造商为了降低零售商的信息租金而向下进行了更大程度产能扭曲，与垄断定价中的“顶端有效率”现象一致。

3.2 产能再分配

表3 四个典型算例

4 结论

信息不对称和双重边际效应是供应链运作过程中普遍存在的现象，如何实现供应链的信息共享，进而降低信息不对称和双重边际效应对供应链运作效率的影响，是当前理论界和实业界研究的重点。在供应链的运作过程中，具有信息优势的分销商向供应商传递虚假信息，以牟取利益，从而导致供应链成员收益的减少和供应链效率的降低。本文以供应商、分销商组成的供应链为背景，运用信息经济学机制设计理论对供应商的产能决策和分配进行了研究。

当前，关于信息不对称环境下的供应链协调问题还没有形成非常成熟的体系，本文针对存在多销售渠道的能力计划与分配问题构建了产能预定合同，并在此基础上提出了产能再分配模型。研究结果显示，通过显示原理，设定恰当的产能预定合同菜单，可以使分销商真实显示私有预测信息，据此得到最优合同形式和最优决策。当然，本文的一些结果是在假定需求信息为特定分布条件下所得到的，推广时还需要进一步地验证。但是，本文通过量化的方法为实践中的决策者提供了一种管理的视点：分销商的预定产能中蕴含着有效的信息，供应商可以据此推断市场的真实需求信息；引入直销市场可以有效的降低预测失误导致的产能过剩和不足的风险；当信息更新后，对合同参数进行再优化可以激励分销商提高预测精度从而达到改善供应链绩效的目的。

现有供应链协调的研究基本上都集中在一次性的供应链伙伴合作关系的前提之下，而实践中更常见的情况是供应链成员之间的伙伴合作关系是稳定的、长期存在的[15]。因此对于长期合作关系下具有跨期关联的非对称信息供应链协调问题[20]将是下一步研究的方向。

[1] Wang KZ, Jiang ZB, Li N, Geng N. Optimal Production Control of a Service-oriented Manufacturing System with Customer Balking Behavior[J]. Flexible Services and Manufacturing Journal, 2012,1:1-21.

[2] 江宏，赵皎云.上海标五：物流助力企业转型发展[J]. 物流技术与应用, 2010, 9: 56-62.

[3] Clay K, Krishnan R, Wolff E, Fernandes D.On the web:Price and non-price competition in the online book industry [R].Working paper, Carnegiemellon University, mimeo, 2000.

[4] Aviv Y. A time series framework for supply chain inventory management [J]. Operational Research, 2003,51(2): 210–227.

[5] Cachon G. The allocation of inventory risk in a supply chain: Push, pull and advance-purchase discount contracts [J]. Management Science, 2004, 50(2): 222–238.

[6] Erkoc M, Wu D. Managing high-tech capacity expansion via reservation contracts [J]. Production Operational Management, 2005,14(2) : 232–251.

[7] Erhun F, Keskinocak P, Tayur S. Sequential procurement in a capacitated supply chain facing uncertain demand[R]. Working paper, 2003, Stanford University, Stanford, CA.

[8] Lau A, Lau H. Some two-echelon style goods inventory models with asymmetric market information [J]. Europe Journal of Operational Research, 2001,134(1): 29–42.

[9] 索寒生, 金以慧．非对称信息下供需链中供应商的回购决策分析[J]．控制与决策, 2004, 19:335-338.

[10] 唐宏祥, 何建敏, 刘春林．非对称需求信息条件下的供应链信息共享机制[J]．系统工程学报, 2004，19(6):589-595.

[11] Iyer A, M Bergen. Quick response in manufacturer-retailer channels [J]. Management Science,1997, 43(4): 559–570.

[12] Fisher M, A Raman. Reducing the cost of demand uncertainty through accurate response to early sales [J]. Operational Research,1996,40(1): 87–99.

[13] Ozer O. Replenishment strategies for distribution systems under advance demand information [J]. Management Science, 2003, 49(3): 255–272.

[14] Barnes-Schuster D, Bassok Y, Anupindi Y. Coordination and flexibility in supply contracts with options [J]. Manufacturing Service Operational Management , 2002, 4(3): 171–207.

[15] Puettmann C, Stadtler H. A collaborative planning approach for intermodal freight transportation [J]. OR Spectrum, 2010, 32(3):809-830.

[16] Ozer O, Wei W. Strategic commitments for an optimal capacity decision under asymmetric forecast information [J]. Management Science, 2006, 52(8):1238-1257.

[17] 浦徐进,石琴,凌六一.直销模式对存在强势零售商零售渠道的影响[ J].管理科学学报, 2007, 10(6): 49-56.

[18] 黄健，肖条军，盛昭瀚.多渠道供应链管理研究述评[J], 科研管理, 2009, 30(5): 25-32.

[19] Fudenberg D, Tirole J. Game Theory [M]. Cambridge MA: MIT Press, 1991.

[20] Thomas J. Income fluctuation and asymmetric information: An example of a repeated principal-agent problem [J]. Journal of Economic Theory, 1990, 51(2):367-390.

Capacity Management with Direct Selling Demand under Asymmetric Demand Information

XIE Wen-ming1,2, JIANG Zhi-bin1,2, LIU Cong1,2,CHU Yi-bing1,2

(1.Sino-US Global Logistics Institute, Shanghai Jiaotong University, Shanghai 200240, China; 2.School of mechanical Engineering , Shanghai Jiaotong University, Shanghai 200240, China)

Capacity planning plays an important role in the strategic decision making process for many companies. Its applications can be found in many industries, including communication networks, electric utilities, service, electronic goods and semiconductor industries. In all of these applications, building manufacturing capacity requires the commitment of substantial capital resources over a long period of time. Furthermore, multi-channel distribution and uncertainties in the long range forecasts for cost and demand in supply chain make these decision problems extremely complex. We use an actual case to explain the complexity.

We study the problem of assuring credible forecast information sharing between a supplier and a distributor. In order to improve supply chain performance, direct selling market is introduced to the supply chain. A corresponding two-stage decision-making mechanism is proposed to solve capacity planning and distribution problems in the multi-channel supply chain. Before the demand information is obtained, capacity reservation contract is designed, which enables distributors to share private demand information with suppliers via reserve capacity. After the demand information is updated, four capacity allocation polices are identified to maximize the profit of suppliers.

Different from literatures on information sharing in supply chains that has focused primarily on statistic and symmetric information with single distribution channel, we propose capacity planning and allocation problems with asymmetric information and multi-channel distribution. The supply chain follows the pattern of decentralized supply chains under information asymmetry. Thus, there are serious double-marginal and bullwhip effect in the supply chain. In this research, we investigate the efficiency of capacity reservation contract within a simple supply chain with direct selling channels. We study capacity planning as well as distribution of updated information. A two-stage decision-making mechanism is developed to improve manufacturing capacity planning and allocation performance in the supply chain. The first stage is to determine the capacity of a manufacturer, and the second is to reallocate capacity between the service provider and the direct selling market.

We show that under capacity reservation contract the manufacturer and the system always benefit from information sharing. In addition, reservation capacity will be closed to centralized reservation capacity when the service provider’s forecast is sufficiently high. Based on this research, allocation policies are proposed for different scenarios. Numerical experiments show that it is efficient to solve manufacturing capacity planning and allocation problems by using the proposed decision-making mechanism.

asymmetric information; information screening; mechanism design; contract

中文编辑：杜 健；英文编辑：Charlie C. Chen

F274

A

1004-6062(2016)01-0197-08

10.13587/j.cnki.jieem.2016.01.025

2012-02-23

2012-03-02

国家社会科学基金资助项目（70932004）；博士点基金项目（20090073110035）；上海市教委2009年度科研创新重点项目(09ZZ19)

谢文明（1984—），男，蒙，内蒙古赤峰人。上海交通大学博士生，研究方向：合同理论。