基于价格信息的期货市场交易操纵模型及其应用

蒋云鹤，刘海龙



基于价格信息的期货市场交易操纵模型及其应用

蒋云鹤，刘海龙

（上海交通大学安泰经济与管理学院，上海 200052）

在Kyle、Viswanathan[1]研究基础上，提出价格信息对交易的敏感程度是影响操纵的首要因素，通过模型证明了操纵者收益是其所获得信息优势的单调增函数。当价格信息对交易变得敏感时，大交易者会通过交易尽可能获取最大的信息优势，价格信息中个人信息越多，合约被操纵的可能性就越大。掺杂了大量个人信息的合约价格即虚假价格，虚假价格会掩盖供求关系并“欺骗”其他交易者，诱使他们帮助操纵者获利并掩盖操纵事实。以此为基础，提出了一种考察不同时期个人信息数量的计量方法。对价格信息的进一步研究发现，被操纵合约同品种中其他合约的价格发现功能也会不同程度扭曲，距被操纵合约越近所受到影响越大。选取2010年、2011年和2012年九月棉花期货作为检验样本，进行了实证检验。实证检验的结果与所提出观点高度一致，进一步证明和强调了模型的实用性和有效性。

期货市场；操纵；信息优势；价格发现

0 引言

期货市场操纵是指交易者利用资金优势，控制期货价格牟取超额利润的行为。期货市场操纵分为逼仓和挤榨两种情况，当交易者通过同时控制期货市场和现货市场以控制价格的行为称之为逼仓（Corner），以利用、恶化现货市场拥塞（Market congestion）为手段来控制期货价格的行为称为挤榨（Squeeze）[2]。期货市场操纵问题由来已久，美国期货市场建立的前五十年中有记录的操纵案例就多达124次[4]。市场操纵行为极大的损害了期货市场投资者的利益，严重的还会导致市场关闭。作为一个新兴期货市场，近年来发生的期货市场操纵行为严重影响了我国期货市场的健康发展，操纵问题的研究也成为我国理论和实务界越来越关注的问题。

期货价格是风险信息和供求信息最重要的传递渠道，合理的价格是市场有效性的根本保证。市场操纵行为严重的阻碍了价格信息的正常传递，扰乱了套期保值者的正常交易，损害了期货价格的导向作用，而风险转移和价格发现正是期货市场最基本的两项重要功能。在监管中，市场信息的扭曲往往被看成是存在操纵的重要证据。2009年美国证监会(SEC)和美国商品期货交易委员会(CFTC)的联合报告认为市场信息扭曲是识别操纵的重要标准之一，“市场价格应当是总供求关系的体现，当总供求关系被不合理交易所掩盖而产生虚假价格，那么就可以认定为操纵”[6]。中国《期货管理条例》七十四条规定，操纵行为的重要特征之一就是“单独或者合谋，集中资金优势、持仓优势或者利用信息优势联合或者连续买卖合约，操纵期货交易价格的……”。可见，从价格信息角度分析操纵问题是市场管理者亟需而且可行的，由此得出的理论模型对市场监管者维护市场秩序和市场功能具有十分重要的现实和理论意义。

近年来，许多学者对市场操纵进行了大量的研究，得出了许多重要结论。期货市场理论研究认为交割制度、交易制度和信息不对称是导致操纵发生的三个主要原因。Pirrong用“残局”模型（end game）证明了在接近到期日时，由于交割成本导致空头的交割成本要大于平仓成本，交易者完全有可能通过操纵获得超额收益[8]。Jarrow证明操纵的根源在于“歧视性价格拍卖”[10]。Allen、Gorton在Glosten-Milgrom模型[12]的市场条件下，考虑了一个纯交易基础的非知情交易者的操纵模型，说明市场中自然存在的信息不对称就可以使交易策略操纵获利[14]。Chakraborty, Yilmaz将知情者交易与Glosten-Milgorm模型结合，让知情者反复交易，得出结论:只要市场面对知情交易者的不确定性，交易的时间足够长，均衡必有操纵[16]。

国内操纵研究主要局限于操纵识别与预测，主要通过各种数学工具区分操纵交易日和非操纵交易日，进而识别操纵行为。迟国泰，刘轶芳，余方平选用资金、价格、持仓量等三类指标来反映期货交易中的操纵风险，采用非线性映射分析将交易中存在操纵风险的交易日分离成独立的点群，根据离差极小、最大欧氏距离等原理提出操纵风险阀值计算方法及操纵风险判定方法[17]。迟国泰、刘轶芳、余方平采用期货价格波动风险、持仓量波动风险和基差波动风险二大因素衡量期货交易中的操纵风险，采用KLR信号分析法、SV随机波动模型、GARCH模型等构建了操纵风险预警模型[18]。黄伟、刘海龙从库存、持仓量以及期现基差三方面构建了期货市场操纵风险指标。从持有成本、持仓库存关系角度推导出指标的合理上限值作为阀值，采用分位数阀值法与固定阀值法相结合的阀值确定方法识别操纵风险，为期货市场操纵风险的预警以及监控提供理论基础以及实务操作方法[19]。鲁姣、阎春宁、侯卜魁选取期货价格波动率、持仓量波动率和收益率三个指标，通过加权得到了一个综合衡量操纵风险的信号值，并籍此建立了预警期货市场操纵风险的模型[20]。熊熊、张宇、张维、张永杰通过建立Logistic回归模型，将股指期货是否被操纵的问题转化为根据一定时期内股指期货操纵时间的预警模型[21]。

总的来说，操纵研究大多是在kyle[22]和Glosten[12]的基础上展开，认为操纵者的信息地位是掌握操纵地位的根本保证，这种信息可以是操纵者在参与交易前就获得的（信息操纵），也可以是操纵者通过交易策略所获得的（交易操纵）。从操纵的界定来看，近年来越来越多的学者[1, 23-26]认为破坏市场效率的行为就可以认定为操纵，市场效率以市场价格信息的有效性和市场流动性为标准。尽管如此，大多数研究仍然选择操纵者交易策略为研究对象。可是在实践中，市场操纵者的交易策略只能通过司法途径才能获得，数据的难以获取在很大程度上制约了实证研究的发展，这也是目前的操纵理论研究与实证研究相脱节的重要原因。本文认为操纵的研究思路应从交易策略扩展到信息地位研究，才能够更好的将操纵理论研究应用于实际。

随着各国期货市场法律的不断健全，操纵者也面临着越来越大的风险，如操纵失败后的法律制裁和损失。因此，市场操纵逐渐由一年或者几年的长期行为转变为仅有数月而且更加隐蔽的短期行为。短期操纵相比之于长期操纵，操纵者所获得收益会变小。如果没有任何内幕信息，为获取同样的信息地位，相同时间内短期操纵比长期操纵需要投入更多资金，而这会为操纵者带来更大的风险。可操纵者为什么还要这样做呢？本文结合市场价格信息来识别操纵行为，为操纵研究提供一个新思路。本文认为影响操纵者是否选择操纵市场的首要因素并不是采取何种交易策略，而是操纵者能否迅速而且隐蔽的获取信息优势。市场价格信息对操纵者交易越敏感，操纵者的个人信息就越容易取得信息优势，操纵者也越有可能在短期内获取超额收益。当现货价格受到某些意外因素的影响而发生剧烈波动时，操纵者通过交易或者内部信息所获取的信息优势就能够“欺骗”无信息优势交易者帮助自己在短期内完成操纵。在此基础上，本文提出了一种切实可行的操纵识别方法。

此外，现有研究还较少涉及到合约操纵对整个期货品种的影响。本文认为期货价格是所有交易者在当前对于到期日期货价格与仓储费用的期望，当操纵发生时操纵者将大量的个人信息融入市场信息之中，会导致其他合约交易者对仓储和供求信息的误判。因此，一旦某个合约被操纵，整个品种的价格发现能力都会受到影响。

1 假设

假设1交易者假设

市场中存在许多噪声交易者和一个大交易者①大交易者定义为其交易能够影响市场价格交易者，详见Robert and Jerrow[10]、David J.Cooper[3]、Kummar and Seppi[5]等，所有交易者都是理性交易者而不掌握内幕消息。大交易者拥有初始资产现金，其中有数额用以购买存续期为T的商品期货合约，持有现金没有净收益。大于或者小于0表示大交易者的交易方向，表示做多，表示做空。在时刻t合约价格是，大交易者手头合约若全部平仓所能获得现金流为，此时大交易者的现金流是。

假设2期货市场假设

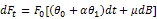
假设3交易者效用假设

理性交易者效用函数的相关研究有很多，很多学者的研究都指出均值方差效用函数能够很好的描述交易者行为②均值方差效用函数在描述交易者收益时表现很好，对此效用函数的具体描述请参见相关文献如，Gagnon Lypny and McCurdy[7],Lafuente andNovales[9], Lee、Yoder、Mittelhammer and McCluskey[11]等。本研究选取指数函数作为交易者的效用函数，其中。

2 模型

由假设3，有大交易者在时刻t的效用函数H

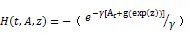
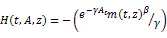
(1)

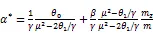
由式（2）有，

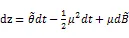
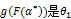
随着价格波动增大，噪声交易者发现市场中存在大量个人信息，会减少市场流动的“供给”。Marco pagano and Ailsa Roell[27]、Kyle[1]等研究指出，个人信息的存在对于流动性提供者存在负外部性影响（negative externality），操纵行为会降低市场流动性、削弱价格发现功能。由于大量个人信息的存在，此时的市场价格不能反映真正的供求关系因此被称为虚假价格，而虚假价格就可以看作是被操纵的证据④被操纵的价格就是虚假价格，虚假价格就是被操纵的证据，详细请参见Kolb, R.W. and Overdahl, J.A.[13]

引理3即使只有某一合约被操纵，在此期间交易的其他合约的发现功能也会受到影响。从价格发现角度来看，期货价格是当前对到期日价格的估计。因此，当套期保值功能受到影响时，真实溢价的波动就会增大。

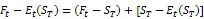
其中，风险溢价可以进一步分解，

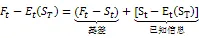
真实溢价可以表示为三部分组成，

（4）

由上式，合约价格是由库存量（反应的是市场的供求状况）、利率、仓储成本和时间所组成。由仓储理论(theory of storage)，合约价格中还应包含便利收益，便利收益是指持有存货的交易者可以更加主动参与交易，因此便利收益的存在通常会使式（5）小于0⑥便利收益也解释了为什么交易者在现货价格比期货价格高的时候也不一定愿意出售现货，详细内容请参见Hull[15]。。由推论2，操纵所造成的虚假价格会导致供求信息失真，而不同到期日合约的价格信息是交易者判断便利收益的主要依据，所以操纵会影响同品种中其他合约交易者对便利收益的判断。因此，在操纵期间进行交易的同品种所有合约的基差都会受到不同程度影响，距离被操纵合约时间越远所受影响越小。因此式（4）中的基差部分会由于其他合约的操纵而受到影响。

接下来分析已知信息部分对操纵的反应。现货价格与到期现货价格期望之差反应的是市场中的已知信息，表示交易者通过当前的现货信息和其他合约的供求信息可以不断修正到期日现货价格的期望。由推论2，操纵者的个人信息会导致市场价格发现功能的减弱，因此其他合约交易者对到期日价格的判断会变得更加困难。可见，该品种所有在此期间进行交易合约的价格预期都会受到影响，距离被操纵合约时间越远所受影响越小。所以式（4）中的已知信息部分会由于其他合约的操纵而受到影响。

综上所述，所有在操纵期进行交易的同品种合约真实收益波动都会变大，越是临近被操纵合约波动越大。根本原因在于，大交易者能够在某个合约中融入大量的个人信息，却并不会将这一个人信息与市场“分享”，降低了整个品种的信息透明度。具体体现就是，在剔除未知风险影响之后，整个品种操纵时期的真实收益波动会显著大于其他时期。

根据以上分析可以得到两个结论：

推论1 由引理1、2，市场价格对交易者交易越敏感时，大交易者会在价格信息中掺杂更多个人信息即越大，该合约被操纵的可能性越大。

推论2 由引理3，若某一时期内有合约被操纵，那么同品种中其他合约的价格发现功能也会受到影响，且越临近被操纵合约受到影响越大。

3实证检验

3.1数据

中国棉花消费量占世界棉花产量45%左右，郑州商品交易所也是世界最重要的棉花期货交易所之一。受我国棉花生产周期影响，一般新年度棉花会在10月份左右上市，而上一年度的棉花到9月时库存已经不多。这就使每年的9月合约市场投机氛围浓厚，发生市场操纵的可能性增大。棉花9月合约近年来被传发生了多起操纵事件，例如被《证券时报》等多家媒体报道的合约CF1009操纵事件⑦详细内容请参见Hull[15]。。一般情况下，由于套期保值用户向远期合约移仓，棉花9月合约持仓量在交割期四月下旬开始逐渐减少。但是，CF1009合约七月持仓量仍然处于较高水平（如图1所示），多头操纵逐渐形成。

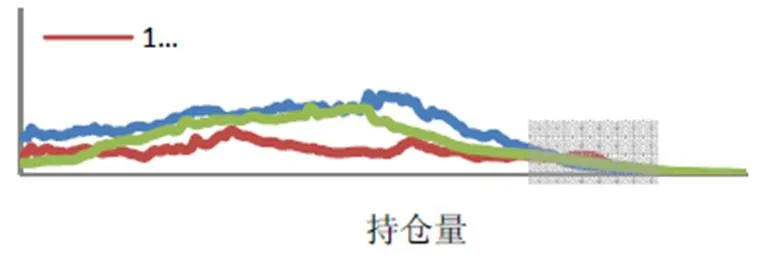
图1 2010、2011、2012年九月合约持仓量

注：阴影部分为各合约七月持仓量

针对这种情况，郑州商品交易所于2010年7月21日发布了交易风险提示函以避免操纵的发生，但操纵仍然给很多投资者带来了巨大损失。因此，本研究选取棉花九月合约作为检验样本。九月合约数据共729个，包括2010年CF1009合约、2011年CF1109合约和2012年CF1209合约各243个。数据来源于郑州商品交易所。使用的统计软件为matlab2007a。

3.2 推论1的实证检验

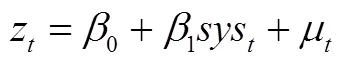
(7)

3.2.1线性回归

3.2.2平稳性检验

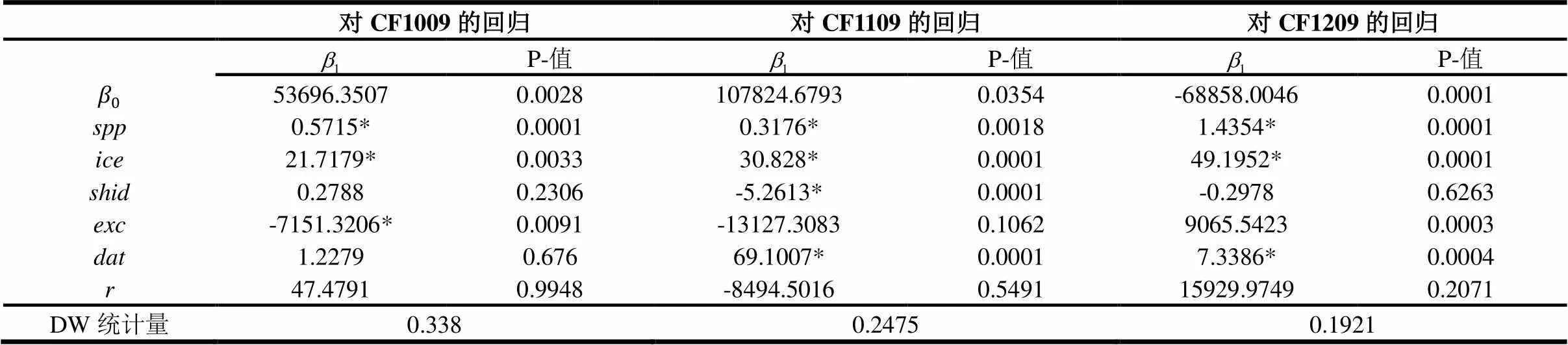
表1 回归结果

注：*表示5%置信水平下拒绝原假设。

表2 平稳性检验结果

3.3.3协整检验和VAR模型的建立

在单位根检验的基础上，使用Johansen方法对变量进行协整检验。并通过考察迹统计量和最大特征根统计量建立VAR模型，以确定、、三者之间的关系。在VAR模型的构建中，一个首要问题就是滞后阶数的确定，太小不能完整反映模型的动态特征，太大就会影响参数估计的有效性。因此，选取LR统计量（5%置信区间）、FPE准则（最终预测误差）、AIC准则（信息准则）、SC准则（信息准则）和HQ准则（Hannan-Quinn）共5个指标进行判断，最终选取滞后阶数为2（如表3）。

表3 滞后阶数选择

注：*表示该指标下最优阶数。

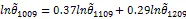
表4 协整关系检验

注：*表示在5%置信水平下拒绝原假设，P-值是Mac Kinnon、Haug、Michelis[30]中的P 值

3.3.4 VECM模型的建立和累积残差计算

在前文的基础上，估计向量误差纠正模型（如表5所示），得到表达模型。对VECM进行LM检验，发现存在ARCH效应。将VECM的残差设为ARCH形式，由于条件方差方程的残差平方滞后项为1阶，因此假设残差分布服从t分布，即。以算法BHHH通过极大似然法对参数进行估计，结果非常显著（如表6所示）。籍此结果对VECM进行标准化（），并得到CF1009在各时点的累积残差。由U法检验（如表7所示）发现，偏度小于零且说明数据分布左偏，峰度不等于0且p值很大说明数据风度系数为0，因此累计残差数据服从正态分布。

表5 向量纠正模型

注：、、分别为CF1009合约、CF1109合约、CF1209合约一阶滞后项，括号内为P值

表6 ARCH估计

注：小括号是标准差，中括号是z-统计量。

表7 正态检验

表8 累计残差表

注：六月共有19个交易日，七月有22个交易日

3.2推论2的实证检验

推论2考察的是不同时期合约的价格发现功能，由于期货价格是到期日现货价格的预期，因此选择真实收益为检验对象。为了单独考察操纵的影响，与推论1检验相类似，首先以式（6）剔除其他因素所引起的价格波动，由于计算真实溢价所以回归中不包括现货价格。在操纵时期和非操纵时期，按照与CF1009的距离进行分类，系统观察整个棉花期货是否受到了CF1009合约操纵的影响。

3.2.1数据分类

数据分类的初衷是为了便于全面考察期货品种在被操纵期内所受到的影响，因此将数据分为操纵时期和非操纵时期两大类（如表9所示）。在此基础上按到期日不同又将合约分为三种，CF1指的是在选定窗口期内考察的合约，CF2、CF3是第二远期合约、第三远期合约。例如，Ser01中CF1指的是存在操纵时期的6、7月间交割的合约，那么CF1就是指CF1007合约，相应的CF2、CF3就是CF1009和CF1011，依此类推。

表9 数据分类

3.2.2剔除系统风险

由于这里要将三个不同时期的实际溢价进行对比，因此有必要进行标准化，即。按照式（6）对各时期的价格进行回归，目的是剔除系统风险，其中不包含现货市场数据。由于对各个变量与真实溢价之间的关系进行了简化（只考察了线性关系），因此回归的结果并不一定具有直接的经济含义。

3.2.3残差方差

通过前面的回归可以得出在不同时期的残差方差（表12、表13），可以发现几个特别之处。

首先，可以发现所有操纵时期的残差方差都要明显大于非操纵时期，说明在操纵时期间整个棉花期货真实溢价波动要大于非操纵时期。可见，CF1009合约价格发现功能的下降也波及到了其他合约，致使整个市场的波动加大、价格发现功能下降。

其次，在ser01（2010年6、7月）和ser02（2010年5～8月）中，CF2（CF1009）合约的真实溢价波动是最大的，说明CF1009的价格发现功能所受到的影响最大，而此合约也正是被操纵的合约。

第三，在ser01（2010年6、7月）和ser02（2010年5～8月）中，CF1（CF1009）的波动显著大于非操纵时期。剧烈波动主要是两个原因，一是CF1009的操纵干扰了在此期间交割的CF1007，二是青岛“5.20”大火⑨5月20日,一名陌生人突然闯进青岛保税区棉花仓库纵火，相关报道详见http://news.hexun.com/2010-07-05/124149431.html导致可供交割的现货不足加剧了波动。

第四，纵观ser01和ser03（2010年6、7月间进行交易的所有合约），发现所有合约的真实溢价波动都有不同程度的增加。被操纵合约CF1009波动最大，其他合约随距离越远波动越小，而且都显著大于非操纵时期。可见，CF1009合约的操纵不仅仅是对单一合约价格发现功能的破坏，对整个棉花期货的价格发现能力都产生了影响。

4 结论

本文在Kyle、Viswanathan[1]等学者研究基础上，认为交易者所获得的信息地位才是判断和研究操纵的关键，而交易策略并不重要。基于对信息优势的研究，本文认为由于操纵本身的风险越来越大，只有市场由于某些事件而变得敏感时，操纵者才会通过交易“欺骗”其他交易者帮助自己取得操纵地位。当价格信息中交易者个人信息明显多于其他时期，合约价格已经不能正常反应市场信息而形成虚假价格时，就可以断定操纵行为的存在。当操纵形成时，由于大量个人信息的存在合约的价格发现功能会受到极大损害。从价格发现角度来看，各合约价格是当前对到期日价格的估计，因此某个合约的操纵会影响整个品种的价格发现功能，体现为真实收益波动变大，距被操纵合约越远所受影响越小。

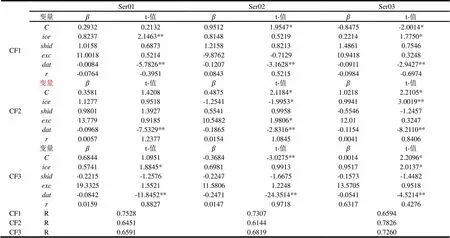
表10存在操纵期间

Ser01Ser02Ser03 变量t-值t-值t-值 CF1C0.29320.21320.95121.9547*-0.8475-2.0014* ice0.82372.1463**0.81480.52190.22141.7750* shid1.01580.68731.21580.82131.48610.7546 exc11.00180.5214-9.8762-0.712910.94180.3248 dat-0.0084-5.7826**-0.1207-3.1628**-0.0911-2.9427** r-0.0764-0.39510.08430.5215-0.0984-0.6974 CF2变量t-值t-值t-值 C0.35811.42080.48752.1184*1.02182.2105* ice1.12770.9518-1.2541-1.9953*0.99413.0019** shid0.98011.39270.55410.9958-0.5546-1.2457 exc13.7790.918510.54821.9806*12.010.3247 dat-0.0968-7.5329**-0.1865-2.8316**-0.1154-8.2110** r0.00571.23770.01541.08450.00410.8406 CF3变量t-值t-值t-值 C0.68441.0951-0.3684-3.0275**0.00142.2096* ice0.57411.8845*0.69810.99130.95172.0137* shid-0.2215-1.2576-0.2247-1.6675-0.1573-1.4482 exc19.33251.552111.58061.224813.57050.9518 dat-0.0842-11.8452**-0.2471-24.3514**-0.0541-4.5214** r0.01590.88270.01470.97180.63170.4276 CF1R0.75280.73070.6594 CF2R0.64510.61440.7826 CF3R0.65910.68190.7260

注：*为95%水平下显著，**为97.5%水平下显著

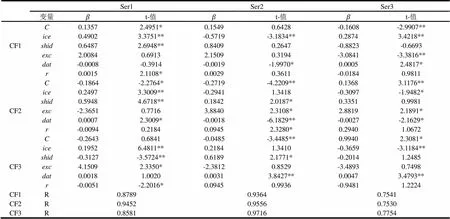
表11不存在操纵期间

Ser1Ser2Ser3 变量t-值t-值t-值 CF1CF2CF3C0.13572.4951*0.15490.6428-0.1608-2.9907** ice0.49023.3751**-0.5719-3.1834**0.28743.4218** shid0.64872.6948**0.84090.2647-0.8823-0.6693 exc2.00840.69132.15090.3194-3.0841-3.3816** dat-0.0008-0.3914-0.0019-1.9970*0.00052.4817* r0.00152.1108*0.00290.3611-0.01840.9811 C-0.1864-2.2764*-0.2719-4.2209**0.13683.1176** ice0.24973.3009**-0.29411.3418-0.3097-1.9482* shid0.59484.6718**0.18422.0187*0.33510.9981 exc-2.36510.77163.88402.3108*2.88192.1891* dat0.00072.3009*-0.0018-6.1829**-0.0027-2.1629* r-0.00940.21840.09452.3280*0.29401.0672 C-0.26430.6841-0.0485-3.4485**0.99402.3081* ice0.19526.4811**0.21841.3410-0.3659-3.1184** shid-0.3127-3.5724**0.61892.1771*-0.20141.2485 exc4.15092.3350*-2.38120.8529-3.48930.7498 dat0.00181.00200.00313.8427**0.00473.4793** r-0.0051-2.2016*0.09450.9936-0.94811.2224 CF1R0.87890.93640.7541 CF2R0.94520.95560.7530 CF3R0.85810.97160.7754

注：*为95%水平下显著，**为97.5%水平下显著

从推论1来看，市场发生操纵的根本原因是不确定性。虽然意外事件的发生不可避免，但能够通过制度上的设计尽量降低此时市场的敏感度。例如本文重点考察的棉花合约CF1009，促使操纵发生的“意外事件”是新疆等棉花主产区天气异常导致收割推迟，随后尽管国储棉开仓平抑市场波动，但操纵者的信息优势已经形成，操纵在所难免。如果市场监管者在消息出现的第一时间对新投机交易提高保证金，提高操纵成本降低市场敏感程度，操纵者就很难在短时间内取得足够的信息优势；如果国储棉明确表示将介入市场之后再逐步放开保证金，虽然以损失一段时间的市场流动性为代价，但操纵极有可能可以避免，从而保证套期保值者的根本利益。

从推论2来看，操纵所削弱的价格发现功能会蔓延至整个品种，这种特点有可能是随着交易者的移仓而传导至其他合约的。更深入地看，期货市场需要保证信息畅通，使期货价格能够反映市场潜在预期，为现货交易提供指导和保证。而操纵的发生破坏了信息的正常传递，势必会导致其他各个合约不同程度上的信息失真。从制度上保证套期保值者顺利参与市场，发挥期货市场套期保值和价格发现的基本功能，这样才能从根本上降低操纵风险。

本文还存在有一定的局限性：

（1）操纵行为的法律界定在我国仍然存在较大难度，为避免争议，本文仅从数理角度来估算操纵发生的概率。

（2）对期货市场产生影响的因素有很多，由于政治和交易制度对价格的影响没有统一观点且难以度量，因此本文在实证检验中只选取了经济变量。

（3）本文所提出观点的前提假设之一是风险中性。虽然大量传统研究的结论支持这一观点，但随着行为科学研究的深入表明投机者在某些情况下表现为风险偏好，这时操纵者的效用函数与假设3也会完全不同。这也是本文继续研究的方向。

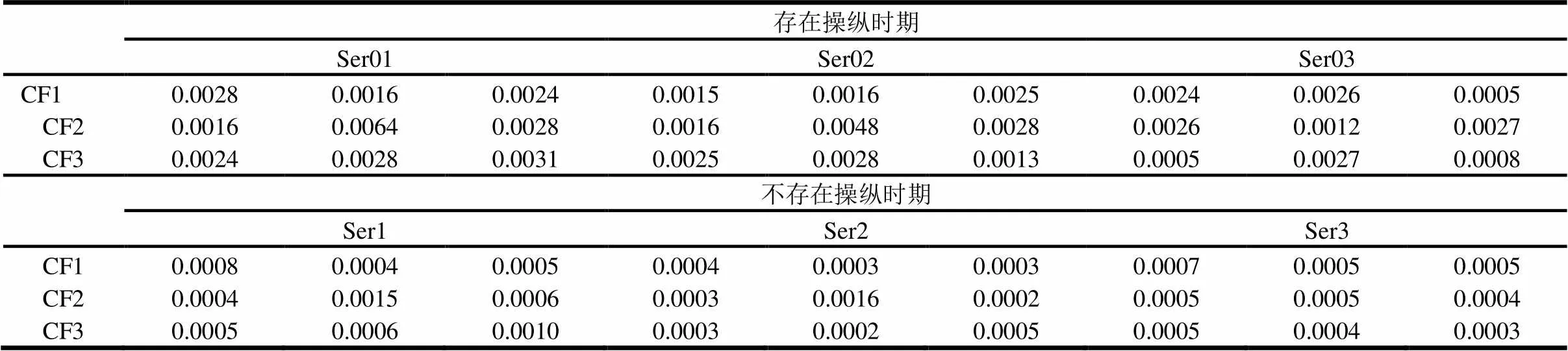
表12 残差的方差-协方差矩阵

表13 不同时期残差方差比较

[1] Kyle A S, Viswanathan S. How to Define Illegal Price Manipulation[J]. American Economic Review. 2008, 98(2): 274-279.

[2] Snider T J. Regulation of the Commodities Futures and Options Markets[M]. Shepard's/McGraw-Hill, 1995.

[3] Cooper D J, Glen Donaldson R. A strategic analysis of corners and squeezes[J]. Journal of Financial and Quantitative Analysis, 1998, 33(1).

[4] Pirrong S C. The Self-Regulation of Commodity Exchanges: The Case of Market Manipulation[J]. JL & Econ. 1995, 38: 141.

[5] Kumar P, Seppi D J. Futures manipulation with “cash settlement”[J]. The Journal of Finance. 1992, 47(4): 1485-1502.

[6] A Joint Report of the SEC and the CFTC on Harmonization of regulation[Z]. 2009.

[7] Gagnon L, Lypny G J, Mccurdy T H. Hedging foreign currency portfolios[J]. Journal of Empirical Finance. 1998, 5(3): 197-220.

[8] Pirrong C. Squeeze Play: The Dynamics of the Manipulation End Game[J]. The Journal of Alternative Investments. 2011, 14(1): 26-39.

[9] Lafuente J A, Novales A. Optimal hedging under departures from the cost-of-carry valuation: Evidence from the Spanish stock index futures market[J]. Journal of Banking & Finance. 2003, 27(6): 1053-1078.

[10] Chatterjea A, Jarrow R A. Market manipulation, price bubbles, and a model of the US Treasury securities auction market[J]. Journal of Financial and Quantitative Analysis. 1998, 33(2).

[11] Lee H, Yoder J K, Mittelhammer R C, et al. A random coefficient autoregressive Markov regime switching model for dynamic futures hedging[J]. Journal of Futures markets. 2006, 26(2): 103-129.

[12] Franklin A, Gary G. Stock price manipulation, market micro structure and asymmetric information[J]. European Economic Review. 1992, 36: 624-630.

[13] Overdahl J A, Kolb R W. Futures, Options, and Swaps[M]. Blackwell Publishing, Oxford, 2007.

[14] Paul G L, Milgrom. Bid, ask and transaction prices in a specialist market with heterogeneously informed traders[J]. Journal of Financial Economics. 1985, 14(1): 71-100.

[15] John H. Options, futures, and other derivatives[M]. Prentice Hall Boston, 2006.

[16] Chakraborty A, Yılmaz B. Informed manipulation[J]. Journal of Economic Theory, 2004, 114(1): 132-152.

[17] 迟国泰, 刘轶芳, 余方平. 基于SV模型和KLR信号分析的期货逼仓风险预警模型[J]. 系统工程. 2006(07).

[18] 迟国泰, 刘轶芳, 余方平. 基于非线性映射分析的期货逼仓风险判定模型及其应用[J]. 系统工程理论与实践. 2006(05).

[19] 黄伟, 刘海龙. 期货市场逼仓风险指标的构建及实证研究[J]. 工业工程与管理. 2008(03).

[20] 鲁姣, 阎春宁, 候卜魁. 中国期货市场逼仓风险预警模型研究[J]. 价值工程. 2008, 27(9): 163-166.

[21] 熊熊, 张宇, 张维, et al. 股指期货操纵预警的Logistic模型实证研究[J]. 系统工程理论与实践. 2011(07).

[22] Kyle A S. Continuous Auctions and Insider Trading[J]. Econometrica. 1985, 53(6): 1315-1335.

[23] Allen F, Litov L, Mei J. Large Investors, Price Manipulation, and Limits to Arbitrage: An Anatomy of Market Corners[J]. Review of Finance. 2006, 10(4): 645-693.

[24] Aggarwal R K, Wu G. Stock Market Manipulations[J]. The Journal of Business. 2006, 79(4): 1915-1953.

[25] Van Bommel J. Rumors[J]. The Journal of Finance. 2003, 58(4): 1499-1520.

[26] Jarrow R A, Protter P. Forward and Futures Prices with Bubbles[J]. International Journal of Theoretical and Applied Finance. 2009, 12(7): 901-924.

[27] Marco P, Ailsa R. The choice of stock ownership structure: agency costs, monitoring, and the decision to go public[J]. The Quarterly Journal of Economics. 1998, 113(1): 187-225.

[28] Dickey D A, Fuller W A. Likelihood ratio statistics for autoregressive time series with a unit root[J]. Econometrica: Journal of the Econometric Society, 1981: 1057-1072.

[29] Kwiatkowski D, Phillips P C B, Schmidt P, et al. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root?[J]. Journal of econometrics, 1992, 54(1): 159-178.

[30] MacKinnon J G, Haug A A, Michelis L. Numerical Distributions of Likelihood Ratio Tests of Cointegration[J]. Journal of Applied Econometrics, 1999, 14(563): n577.

附录

引理1证明

由式（4.3）有，有函数m的线性微分方程

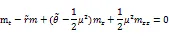
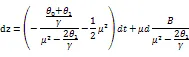
引理2证明

The Model for Trade-based Manipulation in Future Market Based on Price Information and Its Application

JIANG Yun-he1，LIU Hai-long1

（1. Antai College of Economics & Management, Shanghai JiaoTong University，Shanghai 200052, China）

The effectiveness of price information is taken as an important basis to understand risk management in the futures market. The existing research mainly focuses on transaction strategies. The difficulty of acquiring operator’s transaction data results in the disconnection between manipulation theory and empirical study.

Based on Kyle and Viswanathan’s[1]study, this paper proposed that the primary influential element for the operation is the sensitivity of price information to the transaction. The model also proved that an operator’s gains are a single-value raised function of information acquisition advantage. When price information becomes sensitive to transaction, a big dealer will make the maximum information advantage through transactions. Those contract prices mixed with a great deal of private information can be judged as false prices, which hide the actual demand-supply relations and “cheat” on other dealers. These will induce them to help the operator gain profit and hide the manipulating effect. For the above reasons, more attention should be made to the price information in terms of operation risk management in the futures market. Price information should be alerted when the market becomes sensitive because of some uncertain elements. It is important to take some proper measures to avoid the manipulation from occurring. A process of manipulation development is similar to the process of not acquiring enough information for the big dealer. The risk of contract to be operated will increase if the big dealer can rapidly take advantage of the information. Based on this, the writer proposes a computation method to investigate the quantity of private information during all stages. The more private information exists in the price information, the more possibility of contract to be manipulated will occur.

From the information aspect of the futures market, manipulation behavior breaks the demand-supply information’s normal flow between different contracts; hence, the manipulation of a contract will surely impact the finding function of other contract prices within the same variety. The primary cause lies in that a big contractor completes the manipulation with the help of a great deal of the private information existing in the price information. However, the contractor does not “share” this information with the market in order to reduce the information transparency of the whole variety. For other contractors, the closer to the would-be manipulated contract they become, the more influence the information transparency will be subjected to. The observation on the real gain fluctuation shows that the closer the would-be operated contract moves, the more influence the finding function of the contract price can have. Some trading examples of the September cotton futures in 2010, 2011, 2012 are discussed in detail. These examples are used for real evidence verification because the annual cotton contract in September might be one of those contacts with the most feasible atmosphere for domestic gambling. The empirical verification results show a high consistency with the above proposed viewpoints, which verify and strengthen both practicability and effectiveness of the proposed model.

futures market; market manipulation; information superiority; price discovery

中文编辑：杜 健；英文编辑：Charlie C. Chen

F832.5

A

1004-6062(2016)01-0176-09

10.13587/j.cnki.jieem.2016.01.022

2013-07-22

2013-11-18

蒋云鹤（1983—），男，辽宁省沈阳市人。上海交通大学安泰经济管理学院博士研究生，研究方向：期货市场操纵风险管理。