基于创业链声誉的风险投资与风险企业合作的微分对策模型研究

赵黎明，刘 猛，郝琳娜



基于创业链声誉的风险投资与风险企业合作的微分对策模型研究

赵黎明1，刘 猛1，郝琳娜2

(1.天津大学管理与经济学部，天津 300072; 2.南开大学商学院，天津 300071)

利用微分对策理论研究了风险投资和风险企业的合作问题，且基于外部投资者视角将其合作过程抽象为“创业链声誉”的构建过程，构建了一个微分对策动态模型，运用汉密尔顿-雅可比-贝尔曼方程求出风险投资和风险企业在Nash非合作博弈、Stackelberg主从博弈及协同合作博弈条件下的最优策略，并对此三种博弈结构下的反馈均衡结果进行了比较。研究结果显示，协同合作博弈情形下的系统收益、参与双方的收益水平要优于Nash非合作、Stackelberg博弈情形下的收益水平，而风险企业的激励因子是系统中的一种协调和激励机制，可以提高风投和企业以及整个系统的收益。

创业链声誉；风险投资；微分对策；反馈均衡；HJB方程

0 引言

风险投资（Venture Capital），又称创业投资，是指把资金投向蕴藏着较大失败危险的技术创新领域，以期成功后获得高资本收益的一种商业投资行为。而创业企业初创期通常资源匮乏，影响力有限，缺乏广泛而稳定的外部网络联系，缺乏健全的内部组织系统，缺乏成熟企业所具有的信誉和合法性[1]，这些特征可以被统称为新生者不利条件[2]。风险投资作为创新活动融通资金的重要渠道，其在推动创业企业成长和高科技产业发展中的积极作用得到了广泛认同[3]，一方面向创业企业提供资金支持；另一方面，风投对创业企业内部组织的专业化、职能化等很多方面都起着重要的作用[4]。

风险投资作为高新技术产业发展的重要资金来源备受关注，学术界对风险投资的各个方面都展开了积极的研究和讨论，其中风险投资主体与创业企业家之间委托代理关系的研究是风险投资的一个热点。早期的风险投资模型都是假定风险投资是一种单边的委托代理关系，讨论风险投资家如何通过投资契约设计激励与监督企业家努力工作[5,6]，还有大量文献讨论了风险投资主体对创业企业成功的非资金的贡献，包括项目质量信息的提取、公司的监管、管理建议的提供。Gorman Michael等[7]从经验的角度提供了风险投资主体的增值服务的大量事实，Habib等[8]研究了如何利用合约的安排进行信息披露以做合理决策。

国内主要关注于信息不对称及最优合约设计问题，杨青等[9]构造了分析了风险投资中的双重道德风险问题，构建模型就风险投资中如何签订最佳合约以达到对双方的激励进行分析；邓艳红等[10]在双向道德问题的模型下，从讨价还价的角度研究风险投资主体与创业者之间的帕累托有效合约区间的确定问题；郑辉[11]建立了信号传递与甄别模型，详细分析了风险投资过程中存在的逆向选择问题，研究如何解决企业家与风险投资主体之间的信息不对称问题；林朝南等[12]从所有权的性质、控制方式和结构比例等方面实证研究了企业所有权安排对大股东控制权私利的影响；王培宏等[13]给出了多阶段风险投资过程时序模型，得出了多阶段风险投资中控制权转移范围以及主要影响因素对控制权转移范围的影响方向；曾勇等[14]综述了国内外关于风险投资领域的合约订立及治理机制的研究成果，指出风险投资家通过阶段性的风险资本投入以及合约订立能够较为有效地缓解其与风险企业家之间的委托代理冲突；王亚民等[15]通过对证券市场IPO机制的风险企业家激励功能理论分析，发现风险投资可以通过IPO退出形成对风险企业家以公司控制权转移为核心的非现金激励，从而减少两者之间信息不对称问题。刘长贤等[16]研究了委托人对于代理人生产成本为非对称信息的情况下，委托人如何设计最优合约来引诱代理人真实地汇报自己的成本信息的问题，结果表明：委托人的事前信念会影响到最优合约的参数配置；委托人的信息缺失会使其遭受一定的损失，而低成本类型的代理人将能获得额外的信息租金。

在投资契约达成前后，风险投资家与企业家之间一直存在着博弈。对于投资契约形成后的博弈过程，学者关注较多[17-21]，他们通过构建委托代理模型，从监控机制和激励合同的角度出发，探讨契约缔约双方博弈可能采取的策略以及双方的最优权益分配问题,但很少关注投资契约达成前双方的博弈情况及企业家对风险投资家的激励问题。事实上，在投资契约达成前，企业家通常通过提供自有资本等激励措施吸引风险资本[22]，另外，声誉对于风险投资和风险企业而言，是至关重要的，但罕有关于风险投资与风险企业合作的声誉问题的研究。声誉在经济与管理领域的重要作用很早就被不同学科的学者所关注，一般意义上的声誉是种保证形式，它是拥有私人信息的交易一方向没有私人信息的交易另一方的一种承诺。许多组织内的激励机制并不是显性激励，而是声誉等隐性激励。随着高新技术风险投资项目的启动，风险投资家与风险企业家之间的关系是一个随时间推移而不断发生变化的动态过程。而在这个过程中，对于风险投资家来讲，他的利益目标与风险企业的利益并不一致，他是以获取投入到风险企业中所可能实现的风险收益为目的，而不是为了风险企业未来的产品和发展；对于风险企业家来讲，他在与风险投资家合作过程中，为了能够获得风险投资家的后续阶段的投资，可能会隐瞒自己的技术信息，夸大自己的经营业绩以及由于机会成本的存在可能导致的不尽责等。但作为追求自身利益最大化的风险投资家和风险企业家，他们为了自己的长期利益，即考虑为自己建立一种良好的声誉，杜绝机会主义的发生，风险投资便可以赢得良好的声誉以便为风险投资公司募集资金打下基础。同样，风险企业家也能够为企业的长远发展建立良好的声誉。

综上所述，本论文尝试基于“创业链声誉”的概念分析风险投资和风险企业在声誉维护与提高方面的博弈。所谓“创业链声誉”，将其界定为：在风险投资退出时，外部投资者对创业链整体的信任程度。创业链声誉是依赖于创业过程中各方的努力、依时间积累的变量，因此，创业链各成员之间的博弈成为了一个时间不间断的动态博弈。受文献[22,23]关于风险投资和初创企业合作问题的启发，本文将分析基于连续时间的初创企业对风险投资有所激励的双方合作的微分对策模型，与关于风险投资和风险企业合作的已有模型相比本模型的不同之处在于，考虑了在投资契约达成前，通过“激励因子”[23]等激励措施吸引风险资本，同时兼顾实际中的风险投资和初创企业的合作呈现出长期性和动态性的特点，连续时间背景下的博弈充斥着风险投资和初创企业合作的全部过程，由于连续时间对风险投资和初创企业的决策函数的影响非常复杂和难以描述，决策模型难以构建，因此基于连续时间动态博弈的风险投资和初创企业协调问题当前尚缺乏较深入的研究。作为对这个重要领域的一个初步尝试，本文将在分析风险投资和初创企业动态协调及其分析方法和工具的基础上考察基于连续时间的风险投资和初创企业的微分对策。首先分别建立风险投资家和企业家的支付函数，构建微分博弈模型；然后用逆向归纳法分析模型，比较分析了动态环境中Nash非合作博弈及Stackelberg主从博弈的均衡结果。期望所得到的相关结论能为风险企业家和风险投资家在激励问题、努力程度以及选择何种博弈结构等方面的决策提供了理论依据。

1 模型描述（模型与假设）

考察由单个风险投资和单个风险企业组成的创业链，假设风险投资在声誉上的维护与努力水平为，风险企业在声誉上的维护与努力水平为。风险投资和风险企业在创业链声誉维护上的成本函数分别为和，设风险投资和风险企业的声誉维护成本函数分别为：

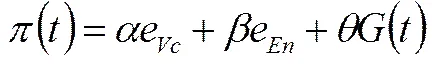
假设创业链的总收益在风险投资和风险企业之间分配，风险投资得，风险企业得，该分配比例是预先给定的，即为风险投资所持有风险企业的股份份额。是风险企业对风险投资的“激励因子”，风险投资和风险企业有着相同的正贴现率，双方的目标都是在无限时区内寻找使自身利润最大化的最优付出努力程度策略。则风险投资的目标函数为

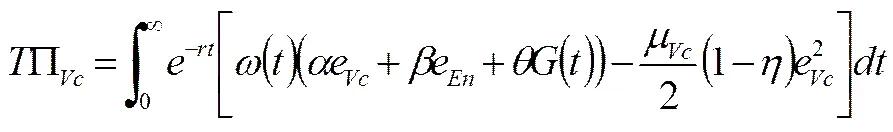
风险企业的目标函数为

(4)

2 Nash非合作博弈

当风险投资和风险企业进行Nash非合作博弈时，双方会同时独立地选择各自的最优努力策略，以最大化自身利润。则博弈参与双方的最优努力策略组合即为静态反馈Nash均衡。

定理1在Nash非合作博弈情形下，风险投资和风险企业的静态反馈Nash均衡策略分别为

(6)

证明 为得到此博弈的Nash均衡，首先假设存在连续有界的微分收益函数，对所有的都满足汉密尔顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman)方程

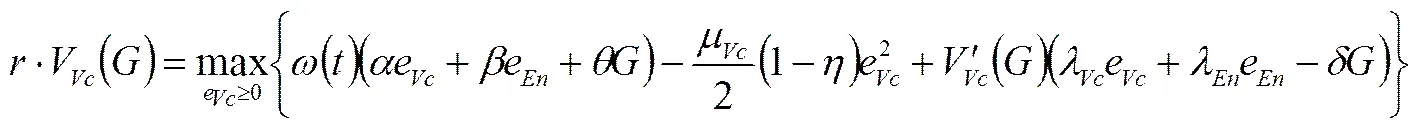
(8)

由(8)式可知，为使自身利润最大化，理性的风险企业在非合作博弈下将不向风险投资提供激励，即。分别对(7)、(8)右端部分求解它们对和的一阶偏导数并令其等于零，解之可以得到

将式(9)代入式(7)(8)，化简整理得到

(10)

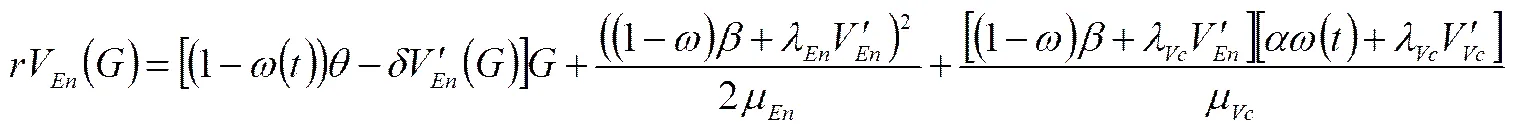
，(12)

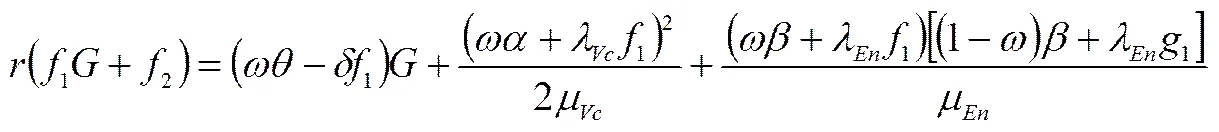
(14)

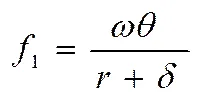
(15)

；

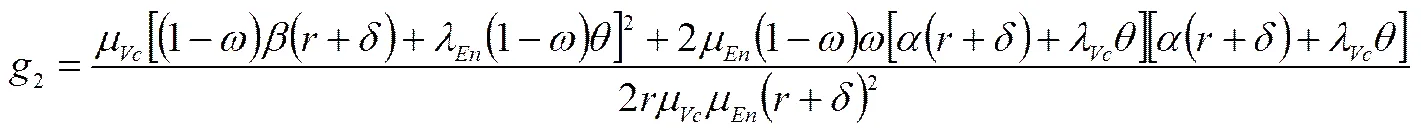
(17)

令，(19)

则(20)

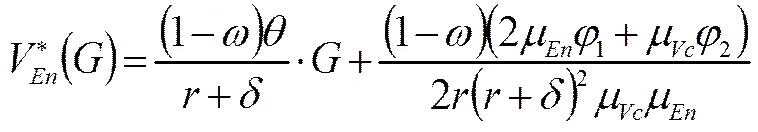
3 Stackelberg博弈

企业家首先选择自有资本投资水平和对风险投资家的激励因子，风险投资家在观察到企业家的行动后，选择总投资水平以及资本结构。因此，双方的投资决策过程可视为Stackelberg博弈过程。企业家是行动的领导者，风险投资家是行动的跟随者。首先分别建立风险投资家和企业家的支付函数，构建博弈模型；然后用逆向归纳法分析模型，讨论了自有资本投资水平和“激励因子”对风险投资家的总投资水平及资本结构的影响。

定理2 在Stackelberg博弈情形下，风险投资和风险企业的静态反馈Nash均衡策略分别为：

(23)

(24)

证明 为得到此博弈的Stackelberg均衡，运用逆向归纳法，首先假设存在连续有界的微分收益函数，对所有的都满足汉密尔顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman)方程。

首先求解VC的最优收益

(26)

风险企业将理性地预测到风险投资将会根据上式选择其努力函数，这时，风险企业的HJB方程为

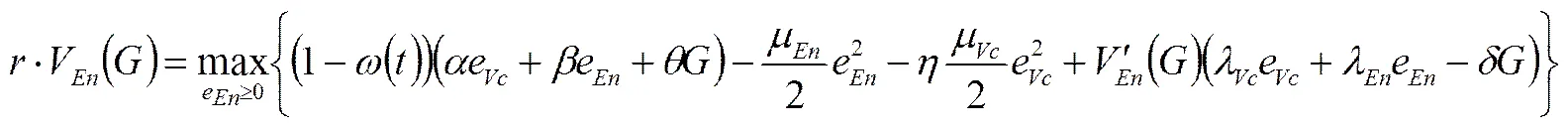
(28)

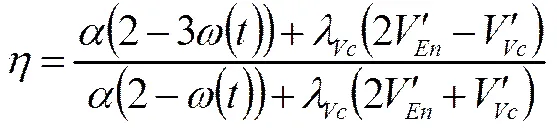
将式(26)、(28)、(29)代入式(25)、(27)，化简整理得到

(30)

由式(30)和式(31)可知，关于G的线性最优收益函数是HJB方程的解，令

，(32)

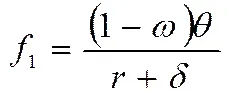
(33)

，

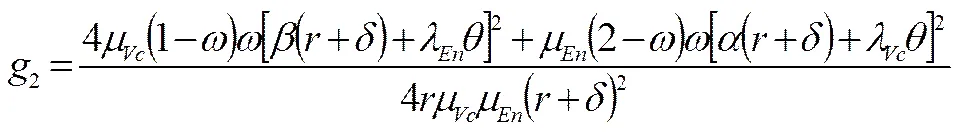
(35)

(37)

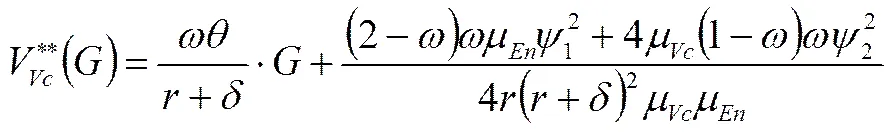
将式(37)和式(38)分别对G求得的导数代入式(26)、(28)和(29)，可以得到式(22)、(23)以及(24)，其中由于，可以得到。证毕□

4 协同合作博弈

风险投资为了在退出时，能够以理想的价格出售给外部投资者，他将会尽力提高创业链的声誉水平，风险企业为显示自身价值吸引外部投资者投资，也将努力提高创业链的声誉水平。本部分重点探讨风险企业和风险投资之间的协同合作关系，并得到了在此博弈情形下风险企业和风险投资的最优努力策略以及创业链整体的最优收益水平。

定理3 在协同合作博弈情形下，风险投资和风险企业的最优努力策略分别为

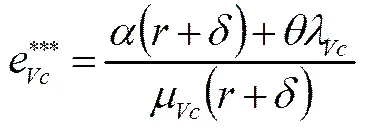
(40)

证明 当风险投资与风险企业之间的关系由非合作过渡到协同合作时，双方以整个创业过程的收益最大化为目标，共同确定和的最优值。则

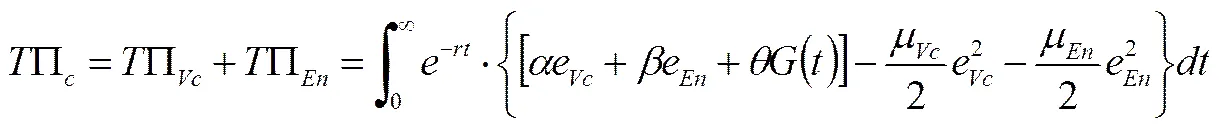
(42)

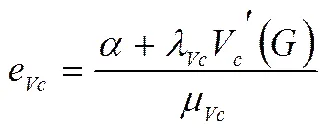
(44)

将式(43) (44)代入(42)，化简整理得到

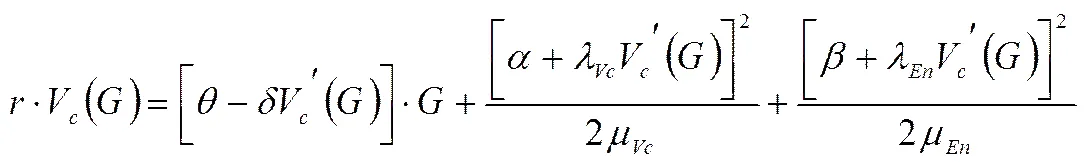
(46)

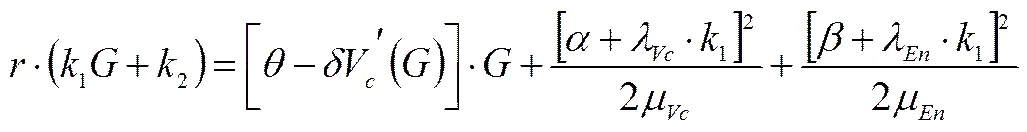
，(48)

代入(46)，可得到孵化网络最优收益函数为

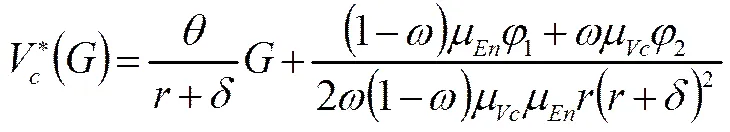
5 均衡结果的比较分析

对Nash非合作博弈、Stackelberg主从博弈和协同合作博弈三种情形下风险投资和风险企业的最优努力策略及整个创业过程的最优收益进行比较，得到相关的一些结论。

随着我国经济的快速发展，商品房的价格始终保持加速增长的势头，这不仅对我国百姓的安居乐业产生影响，也给国家经济发展带来不利影响，因此探索房价的影响因素这个问题是学者聚焦的核心。

(Ⅲ)根据式(5)、(22)和(24)，可知

由定理4可知，当风险投资和风险企业由Nash非合作博弈过渡到Stackelberg主从博弈时，风险投资和风险企业的努力水平变化程度不同，其中风险投资的努力水平与他们的收益分配比率相关，当时，风险投资的努力水平将会提高，并且上升的幅度等于风险企业对风险投资的最优“激励因子”，而风险企业的努力水平将保持不变。而当双方进行协同合作博弈时，最优努力水平将达到最大。

(Ⅱ)根据式(20)和式(38)，

(Ⅲ)根据式(20)、(21)和式(37)、(38)，有

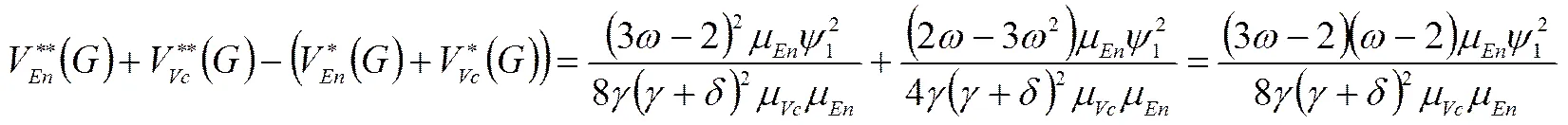
根据式(37)、(38)和(49)可以得到

由定理5可知，与Nash非合作博弈情形相比，风险企业家偏爱Stackelberg主从博弈情形。当时，对整个创业过程的收益而言，Stackelberg博弈要优于Nash非合作博弈，风险投资家的收益增量与他们的收益分配比率相关，若最终的收益分配方案合理可行，那么对风险投资和风险企业来说，协同合作博弈是Pareto最优的。

6 算例分析

风险投资和风险企业在非合作和合作条件下，最佳努力水平和收益水平依赖于模型中的各参数的选择。假设模型中参数值取衰减率，贴现率取，，，，，，，，收益分配比率分别取，则可以得到风险投资和风险企业在非合作条件下的声誉为，所获得收益为，；风险投资和风险企业在Stackelberg合作条件下的声誉为，所获收益为；风险投资和风险企业在协同合作条件下的声誉为，整个创业链的最优收益水平为。

则风险投资和风险企业在非合作和合作条件下，收益水平随时间变化的趋势如图1所示，其中和分别表示的是在Nash非合作博弈情形下，风险企业和风险投资的最佳收益，和分别表示的是在Stackelberg博弈情形下，风险企业和风险投资的最佳收益，表示整个创业链的最优收益水平。

图1情形下风险投资和风险企业的收益比较

7 结论

本文利用微分对策理论研究了风险投资与风险企业合作问题，建立了微分对策模型。运用汉密尔顿-雅可比-贝尔曼方程分别求得了Nash非合作博弈、Stackelberg主从博弈及协同合作博弈下均衡的风险投资和风险企业的努力程度、最优收益情况及风险企业对风险投资的最优“激励因子”，并对博弈结果进行了比较。研究结果表明：(1)“激励因子”是使整个创业链系统以及各成员的收益增加的有效协调机制，是帕累托有效的；(2) 当风险投资和风险企业由Nash非合作博弈过渡到Stackelberg主从博弈时，风险投资和风险企业的努力水平变化程度不同，其中风险投资的努力水平与他们的收益分配比率相关，并且上升或者下降的幅度等于风险企业对风险投资的最优“激励因子”。而风险企业的努力水平将保持不变； (3) 与Nash非合作博弈情形相比，风险企业家偏爱Stackelberg主从博弈情形。当风险投资的收益分配比例时，对整个创业过程的收益而言，Stackelberg博弈要优于Nash非合作博弈，风险投资家的收益增量与他们的收益分配比率相关；(4)当风险投资和风险企业进行协同合作博弈时，双方的努力水平和收益都将达到最优，且创业链的整体收益水平也将达到最优，那么对风险投资和风险企业来说，协同合作博弈是Pareto最优的。最后，通过算例说明了本文模型的应用。

本文的主要贡献为:与以往学者所关注的构建委托代理模型，从监控机制和激励合同的角度出发研究风险投资与风险企业的合作关系不同，本文主要考虑连续时间背景下风险投资和初创企业在合作的全部过程中的博弈，尤其是在投资契约达成前双方就已开始博弈，风险企业家通过自身行为激励风险投资家提供风险资本，即企业家选择自有资本投资水平和对风险投资家的“激励因子”激励风险投资家提供风险投资，尤其是风险投资家投资比例和“激励因子”在风险投资和风险企业契约达成后的整个合作过程中起着至关重要的协调作用，影响着产业链中的博弈双方的努力水平。这些结论阐明了风险投资和风险企业合作的意义，为风险投资家的投资决策及企业家的融资决策（如风险投资家投资规模、企业的股权分配比例、风险企业家自由资本投资水平及其对风险投资家的“激励因子”等）提供建议，也为投资契约的设计提供一定的启发与参考价值。

本文的局限性在于：为利于得到博弈问题的解析解，对相关参数进行了简化。在后续研究中，针对非退化问题寻求微分方程的数值解法将成为重要的方向。同时，进行实践调研的基础上，将论文中基于被抽象了的数学模型所得出的一般化结论，用于分析、指导具体的风险投资与风险企业合作问题，也将具有很强的理论与实践价值。而且本文只考虑了创业链的声誉对风险投资及风险企业的影响，然而影响风险投资和风险企业的因素有很多（风险企业的潜力、风险投资自身的能力等），各因素之间或许是相互作用，相互影响的，这些都有待今后深入研究。

[1] Hallen BL. The Causes and Consequences of the Initial Network Positions of New Organizations: from Whom Do Entrepreneurs Receive Investments [J]. Administrative Science Quarterly, 2008, 53(4):685-718.

[2] 蒋军锋,王修来. 创业利益分割模型研究:基于创业企业家视角的分析[J]. 管理工程学报, 2009,(4):85-90.

[3] Kortum S, Lerner J. Assessing the Contribution of Venture Capital to Innovation [J]. RAND Journal of Economics, 2000, 31(4):674-692.

[4] Casamatta C. Financing and Advising: Optimal Financial Contracts with Venture Capitalists [J]. Journal of Finance, 2003, 58(5):2059-2086.

[5] Bergemann D, Hege U. Venture capital financing, moral hazard, and learning [J]. Journal of Banking& Finance, 1998, 22:703-735.

[6] Susheng W, Hailan Z. Staged financing in venture capital: Moral hazard and risks [J]. Journal of Corporate Finance, 2004, 10(1):131-155.

[7] Gorman M, Sahlman WA. What Do Venture Capitalists Do? [J]. Journal of Business Venturing, 1989, 4(4):231-248.

[8] Habib MA, Johnsen DB. The Private Placement of Debt and Outside Equity as an Information Revelation Mechanism [J].Review of Financial Studies, 2000, 13(4):1017-1055.

[9] 杨青, 李钰. 风险投资中的双重道德风险与最优合约安排分析[J]. 系统工程,2004,131(11):71-73.

[10] 邓艳红, 陈宏民. 风险投资中的双向道德风险与帕累托有效的合约区间——讨价还价的视角[J]. 经济学,2006,5(3):923-928.

[11] 郑辉. 风险投资中逆向选择的解决——信号传递和信息甄别[J]. 工业技术经济,2007,26(3):131-136.

[12] 林朝南,刘星,郝颖. 所有权安排对大股东控制权私利的影响研究[J]. 中国管理科学,2007,15(6):132-139.

[13] 王培宏,刘卓军. 多阶段风险投资过程中控制权转移范围研究[J]. 中国管理科学,2008,16(6):29-32.

[14] 曾勇,郭文新,李典蔚. 风险投资合约及治理机制实证研究综述[J]. 管理科学学报,2008,11(1):110-121.

[15] 王亚民, 朱荣林. 非对称信息下创业投资IPO退出激励机制研究[J]. 管理科学,2003,16(1):37-40.

[16] 刘长贤,田厚平,孙剑平. 逆向选择下供应链业务外包中的最优合约配置[J]. 管理科学学报,2009,12(6):55-61.

[17] 姚佐文,陈晓剑. 可转换优先股与风险投资的有效退出[J].管理科学学报,2003,6(1):92-96.

[18] 赵炎,陈晓剑.不确定环境中风险企业家与风险投资家的博弈分析[J].中国软科学,2003(2):146-151.

[19] 党兴华,权小锋,杨敏利.风险投资委托代理关系中的监控与激励博弈分析[J].科研管理,2007,28(1):155-160.

[20] 晏文隽,郭菊娥.风险投资主体、银行和创业企业家三方委托代理研究[J].管理科学,2009,22(2):91-98.

[21] 郭文新,曾勇.双边道德风险与风险投资的资本结构[J].管理科学学报,2009,12(3):119-131.

[22] Ramy E, Arieh G. A multi-period game theoretic model of venture capitalists and entrepreneurs [J]. European Journal of Operation Research, 2003, 144(2):440-453.

[23] 冯天丽,顾倩,井润田. 企业家自有资本、“激励因子”对风险投资家的激励[J].系统管理学报,2009,18(5):500-505.

Differential Game Models of Cooperation of Venture Capital and Entrepreneur Based on Entrepreneurship Chain Reputation

ZHAO Li-ming1，LIU Meng1，HAO Lin-na2

(1.School of Management and Economics, Tianjin University, Tianjin 300072, China;2.School of Business, Nankai University, Tianjin 300071, China)

Risk investment is an important source of funds for the development of new technology industry. All aspects of risk investment have been actively researched and discussed by academia. Risk investment affects the principal-agent relationship between venture capitalists and entrepreneurs.

Early venture investment model assumes that the relationship of entrepreneur and risk investment is one kind of unilateral principal-agent relationships. The model discusses how venture capitalists design contract to motivate and supervise entrepreneurs to work hard. The current research primarily focuses on information asymmetry and optimal contract design issues. However, there are only a few literatures focusing on entrepreneurs’ incentive problems of venture capitalists. This paper introduces the “incentive scheme” which is a common venture financing tool for risk investment project. The scheme employs the methodology of differential games to investigate the optimal strategy of entrepreneurs and venture capitalists in the Nash non-cooperative game, Stackelberg leader-follower game and coordinated cooperative game in a dynamic setup respectively. The feedback equilibrium outcomes in the three game structures are comparatively analyzed.

In this article, the whole process of cooperation between venture capitalists and entrepreneurs is defined as the business chain. By analyzing approaches and tools used for dynamic entrepreneurship chain coordination, this paper explores an important problem: the differential game for entrepreneurship chains based on continuous time.

In the first section, this paper indicates that the dynamic entrepreneurship chain coordination is based on continuous time. It shows that the optimal decision of a decision-maker (game participant) at one time cannot ensure that the same optimal decision can be made in the following periods. This finding means that a decision-maker’s action (decision variable) is also a function of time. In other words, the games between entrepreneurship chain members are a differential game. Decision makers need to consider reputation and its relation with each other from the perspective of entrepreneurship chain coordination. It is important to learn how to maintain and improve the reputation of an entrepreneurship chain, defined as the degree of outside investors’ trust in entrepreneurship chains when venture capital exits.

The second section proposes hypotheses and a general description of our proposed model. The third section builds members’ differential game model based on entrepreneurship chain reputation, deduces the corresponding Hamilton-Jacobi-Bellman equation, and finds sufficient conditions for the optimal differential equilibrium.

The fourth section runs a numeral analysis, and discovers that the optimal decision of member’s effort in maintaining reputation changes of the entrepreneurship chain over time, and the change stabilizes monotonously. Because the game is closely related to time, the optimal decision at one time may not create the maximum interest for decision makers next time. This finding shows that a dynamic decision based on game time has practical values.

To sum up, this research expounds the value of long-term, stable cooperation for entrepreneurship chains. The profit of venture capitalists or start-ups in the coordinated cooperative game mode is always greater than the profit of venture capitalists or the start-ups in the Nash non-cooperative game mode and Stackelberg leader-follower game mode. In addition, the entrepreneurship chain’s profit in the coordinated cooperative game mode is always greater than that in the Nash non-cooperative game mode and Stackelberg leader-follower game mode. This paper illustrates the reference value for the realization of dynamic coordination between entrepreneurship chain members.

entrepreneurship chain reputation; venture capital; differential game; feedback equilibrium; HJB equation

中文编辑：杜 健；英文编辑：Charlie C. Chen

F224

A

1004-6062(2016)01-0168-08

10.13587/j.cnki.jieem.2016.01.021

2013-07-10

2013-11-19

国家自然科学基金资助项目（70972117）

赵黎明（1951—），男，北京人，管理学博士，天津大学管理与经济学部教授，博士生导师，研究方向：技术与创新管理、区域经济可持续发展。