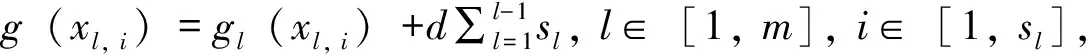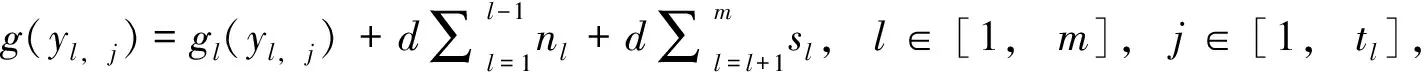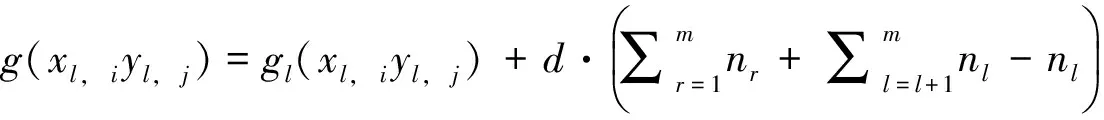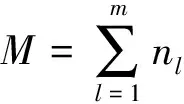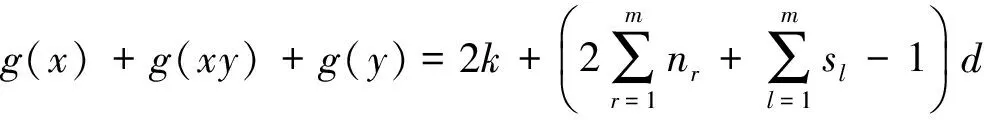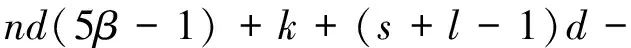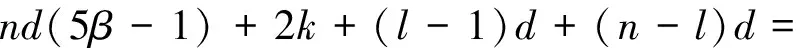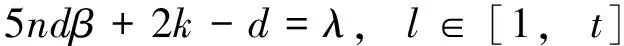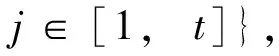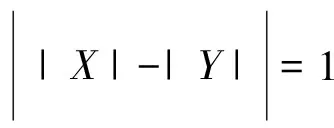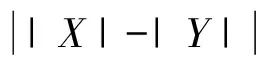探讨树的(k,d)-边魔幻全标号*
2016-06-05赵喜杨
赵喜杨, 姚 兵
(西北师范大学数学与统计学院, 甘肃 兰州 730070)
探讨树的(k,d)-边魔幻全标号*
赵喜杨, 姚 兵
(西北师范大学数学与统计学院, 甘肃 兰州 730070)
研究了树的(k,d)-集有序优美标号和(k,d)-超级集有序边魔幻全标号。通过连接顶点个数较小的(k,d)-集有序优美树的方式, 利用可算法化的构造性证明可得到具有较大顶点数目的(k,d)-边魔幻全标号的树, 建立了(k,d)-集有序优美标号和(k,d)-边魔幻全标号之间的联系。
优美标号; (k,d)-优美标号; 边魔幻全标号; (k,d)-边魔幻全标号
1963年,Ringel猜测:对预先给定的具有n+1个顶点的树, 每一个2n+1个顶点的完全图K2n+1可以被分解为2n+1棵树, 使得这些树均同构于预先给定的树。在研究Ringel猜想的过程中, Rosa发现:如果所有的树都是优美树, 则Ring猜想成立。然而, Rosa的优美树猜想至今没有被证明或否定, 使得这个猜想至今仍是一个吸引人的困难问题。对于数学猜想的进攻, 导致图的着色和标号迅速发展成为当今图论学科中十分活跃的分支, 图的优美标号也成为目前图论研究的一个热点问题[1-12], 他们在编码理论、通讯网络、物流等方面均有着重要的应用。在此基础上发展出了奇优美标号、魔幻标号、幸福标号、(k,d)-优美标号、(k,d)-边魔幻全标号等十多种标号[7-13]。
1 概 念
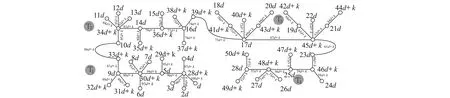
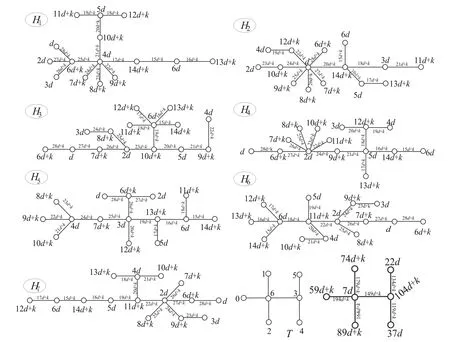
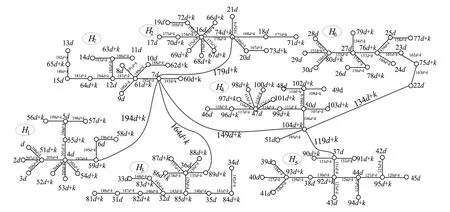
记号[m,n]表示一个非负整数集{m,m+1,m+2, …,n}, 其中m和n均为整数, 且满足0≤m 算法。下面给出本文要用到的几个标号定义。 定义1[10,12]对于给定的(p,q)-图G, 如果存在一个单射f:V(G)→[0,q], 使得边标号集合{f(uv)=|f(u)-f(v)|:uv∈E(G)}=[1,q], 则称f是G的一个优美标号, 也称G为优美图。此外, 若G是具有顶点二部划分(X,Y)的二分图, 且f满足max{f(x) |x∈X} 以下顶点标号集合{f(u) |u∈V(G)}简记为f(V(G)), 边标号集合{f(uv) |uv∈E(G)}简记为f(E(G))。 定义2[10,12]如果(p,q)-图G有一个映射f:V(G)→[0,k+(q-1)d],使得G的任何2个顶点x,y满足f(x)≠f(y), 且定义每条边uv的标号为f(uv)=|f(u)-f(v)|, 当f(E(G))={f(uv) |uv∈E(G)}={k,k+d,k+2d, …,k+(q-1)d} (k,d≥1)时, 则称f是(p,q)-图G的一个(k,d)-优美标号, 也称G为(k,d)-优美图。此外, 若G是具有顶点二部划分(X,Y)的偶图, 且f满足max{f(x) |x∈X} 定义3[10]设G是(p,q)-图。若存在常数λ和双射f:V(G)∪E(G)→[1,p+q], 使对G的任意一条边uv∈E, 总有f(u)+f(v)+f(uv)=λ, 则称f为图G的一个边魔幻全标号,λ为魔幻常数。此外, 若G是具有顶点二部划分(X,Y)的偶图, 且f满足f(X∪Y)=[1,p]和max{f(x) |x∈X} 定义4[10]设G是(p,q)-图。若存在常数λ和双射f:V(G)∪E(G)→{d, 2d, …,μd,k+(μ+1)d,k+(p+q-1)d},μ∈[1,p+q-1], 使对G的任意一条边uv∈E, 总有f(u)+f(v)+f(uv)=λ, 则称f为图G的一个(k,d)-边魔幻全标号,λ为魔幻常数。此外, 若树G是具有顶点二部划分(X,Y)的偶图, 且f满足f(X)={d, 2d, …, |X|d},f(Y)={k+|X|d,k+(|X|+1)d, …,k+(|X|+|Y|-1)d}, 则称f是G的一个(k,d)-超级集有序边魔幻全标号。 定义 5 设H1,H2, …,H|V(T)|和T是树,V(T)={ui|i∈[1, |V(T)|]}。对每一个i∈[1, |V(T)|], 将T的一个顶点ui与树Hi中的一个顶点重合, 得到的图G叫做复合图, 记为G= 引理1 一棵树是(k,d)-集有序优美的充要条件是它具有(k,d)-超级集有序边魔幻全标号。 证明 设n个顶点的树T的顶点集二部划分为(X,Y), 这里X={xi|i∈[1,s]} 和Y={yi|i∈[1,t]},s+t=n。 必要性 设树T有一个(k,d)-集有序优美标号f, 使得 对边xiyj∈E(T), 有 f(xiyj)=f(yj)-f(xi)=k+(s+j-i-1)d 注意到,f(V(T))=[0, (s-1)d]d∪[k+(s-1)d,k+(n-2)d]d和f(E(T))=[k,k+(n-2)d]d。利用f作T的另一个标号g如下: 对边xiyj∈E(T), 令g(xiyj)=nd+f(xiyj) 易知g(xi)∈[d,sd]d,g(yj)∈[k+sd,k+(s+t-1)d]d和g(xiyj)∈[nd+k,k+(2n-2)d]d。进一步, 得到 id+nd+k+(s+j-i-1)d+k+ (s+t-j+1-2)d+d=2k+ (2n+s-1)d 所以, 标号g是树T的一个(k,d)-超级集有序边魔幻全标号。 充分性 设树T有一个超级集有序边魔幻全标号h, 使得h(xi)=id,i∈[1,s],h(yj)=k+(n-j)d,j∈[1,t], 以及h(xiyj)=k+(2n-t-j-i-1)d。注意到h(V(T))=[d,sd]d∪[k+sd,k+(s+t-1)d]d,h(E(T))=[nd+k,k+(2n-2)d]d, 且h(xi)+h(xiyj)+h(yj)=2k+(3n-t-1)d。利用h作T的一个标号α如下: α(xiyj)=h(xiyj)-nd 由于, 故 以上论证说明, 标号α是树T的一个(k,d)-集有序优美标号, 如图1所示。 定理1T1,T2, …,Tm为 (k,d)-集有序优美树。则存在顶点ui∈V(Ti) (i∈[1,m]), 使得用边连接顶点uj与顶点uj+1(j∈[1,m-1])后得 图1 (k,d)-集有序优美标号和 (k,d)-超级集有序边魔幻全标号Fig.1 A set-ordered (k,d)-graceful labelling, and a super set-ordered (k,d)-edge magic total labelling 到的树H具有(k,d)-超级集有序边魔幻全标号。 证明 对l∈[1,m], 设Tl是nl个顶点的(k,d)-集有序优美树, 其顶点集合二部划分(Xl,Yl)满足Xl={xl, i|i∈[1,sl]}和Yl={yl, j|j∈[1,tl]}, 这里sl+tl=nl。由引理1, 树Tl(l∈[1,m])有一个(k,d)-超级集有序边魔幻全标号gl, 使当i∈[1,sl]和j∈[1,tl], 有 以及 2l+(2nl+sl-1)d 对l∈[1,m-1], 用边将树Tl的顶点yl, 1与树Tl+1的顶点xl+1, 1连接在一起, 就得到本定理所要求的树H。利用上述m个超级集有序边魔幻全标号gl(l∈[1,m]), 给树H定义一个标号g如下: (iv)对l∈[1,m-1],Tl与Tl+1之间的连边xl+1, 1yl, 1的边标号为 l∈[1,m-1] 不难验证, 以及 对边xl+1, 1yl, 1∈E(H),l∈[1,m-1], 有 观察图2中的例子, 不难发现, 有多种方法可以将树T1,T2, …,Tm“串联”在一起, 从而构成较大规模的具有(k,d)-超级集有序边魔幻全标号的树。 图2 解释定理1的例子, 其中树H的一个(k,d)-超级集有序边魔幻全标号Fig.2 A super (k,d)-edge magic total labelling of the tree H for illustrating Theorem 1 注意到, 每一棵树Hi有一个(k,d)-超级集有序边魔幻全标号gi, 使得 其中gi(ui)∈Xi,gi(vj)∈Yi, (Xi,Yi) 为V(Hi)的二部划分。显然有 以及gi(ui)+gi(uivj)+gi(vj)=2k+(2ni+si-1)d,i∈[1,p] 根据定理的假设, 所有树Hi(i∈[1,p])的最大独立集的顶点标号均相同, 故可设树H0有一个(k,d)-超级集有序边魔幻全标号g0, 使得 g0(u1) gi(v2)< … 其中g0(ui)∈X0,g0(vj)∈Y0, 且(X0,Y0)为V(H0)的二部划分。同时满足g0(ui)=gl(ui),g0(vj)=gl(vj)i∈[1,s],j∈[1,t],l∈[1,p]。显然,g0(V(H0))=[d,sid]d∪[k+sid,k+(n-1)d]d,g0(E(H0))=[k+nd,k+2(n-2)d]d, 以及 2k+(2n+s-1)d 利用f定义T的一个标号f′为: 接下来, 按照p的奇偶性, 我们分别来找到对称树G*的一个标号g。 (vi) 当l∈[β+1, 2β]时, 令g(ul, i)=k+nd(3β+1-l)+g0(ui)-(s+1)d,i∈[1,s];g(vl, j)=nd(2β-l)+g0(vj)-k+d,j∈[1,t];对边ul, ivl, j∈E(G*), 令g(ul, ivl, j)=nd(2l-3)+g0(uivj)。 下面证明标号g是树G*的(k,d)-超级集有序边魔幻全标号。当l∈[1,β],i∈[1,s]和j∈[1,t]时,Hl的每一条边ul, ivl, j满足 [2k+(2n+s-1)d]=5ndβ+2k-d=λ 当l∈[β+1, 2β],i∈[1,s]和j∈[1,t]时,Hl的每一条边ul, ivl, j满足 k+d+nd(2l-3)+g0(uivj)= nd(3β+1-l+2l-1+2β-l)-d+2k= 5ndβ+2k-d=λ 因为, 当l∈[1, 2β],i∈[1,s], 以及j∈[1,t]时,g(ul, i)+g(ul, ivl, j)+g(vl, j)=λ。故,g是Hl(l∈[1, 2β])的一个使得g(ul, i)+g(ul, ivl, j)+g(vl, j)=λ的标号。 不难发现, 树T和树H的重合顶点具有任意性。对于树T和树Hi(i∈[1,p])的重合顶点来说, 当Hl的顶点ul, i与树T的顶点wl重合时, 用g(ul, i)来替换f′(wl);Hp-l的顶点up-l, s+1-i与树T的顶点wp-l重合时(l∈[1,β]), 用g(up-l, i)来替换f′(wp-l,i)(i∈[1,s]), 然后定义g(wiwj)=f′(wiwj),wiwj∈E(T)。另一方面, 当l∈[1,β], 树Hl的顶点vl, j与树T的顶点wl重合时, 用g(vl, j)来替换f′(wl),Hp-l的顶点vp-l, t+1-j与树T的顶点wp-l重合时, 用g(vp-l, j)来替换f((wp-l, j),j∈[1,t];最后定义g(wiwj)=f((wiwj),wiwj∈E(T)。至此, 对称树G*的标号g已经全部给出。 考察对称树G*的边wiwj的标号, 得到 nd(i+j-i+5β-j)+2k-d= sd+k+(s+t-l)d= 综合上述推理, 可知对称树G*的顶点二部划分(X*,Y*)满足g(X*) 边标号集合g(E(G*))=[k+2ndβ,k+4ndβ-1]。此时,已经得到: (vii) 对每一条边ul, ivl, j∈E(G*),l∈[1, 2β+1],i∈[1,s],j∈[1,t], 有g(ul, i)+g(ul, ivl, j)+g(vl, j)=λ; (viii) 对树T的每一条边wiwj,i∈[1,β],j∈[β+1, 2β], 有f′(wi)+f′(wiwj)+f′(wj)=λ。故当p为偶数时, 标号g是对称树G*的(k,d)-超级集有序边魔幻全标号。 (ix) 当l∈[1,β+1]时, 令g(ul, i)=nd(l-1)+g0(ui),i∈[1,s];g(vl, j)=nd(β+l-1)+g0(vj),j∈[1,t];对边ul, ivl, j∈E(G*), 令g(ul, ivl, j)=2nd(2β+1-l)+g0(uivj)。 (x)当l∈[β+2,2β+1]时,令g(ul,i)=k+nd(3β+2-l)-d+g0(ui),i∈[1,s];g(vl,j)=nd(2β+1-l)+d+g0(vj)(k,j∈[1,t];对边ul,ivl,j∈E(G*),令g(ul,ivl,j)=nd(2l-3)+g0(uivj)。 证明的其余部分完全类似于情形1,故不再赘述。综合情形1和情形2的论证, 定理得证。 图3和图4中给出了说明定理2的一个例子。 图3 (k,d)-优美树H1, …, H7和集有序优美树TFig.3 (k,d)-graceful trees H1, …, H7 and set-ordered graceful tree T 图4 对称树Fig.4 A symmetric tree [1]ZHOUXQ,YAOB,CHENXE.Everylobsterisodd-elegant[J].InformationProcessingLetters, 2013, 113(1/2): 30-33. [2]GALLIANJA.Adynamicsurveyofgraphlabeling[J/OL].TheElectronicJournalofCombinatorics, 2015,DS6.http:∥www.combinatorics.org/ojs/index.php/eljc/article/viewFile/DS6/pdf. [3]BACAM,BERTAULTF,MACDOUGALLJA,etal.Vertex-antimagictotallabelingsofgraphs[J].Discuss.MathGraphTheory, 2003, 23(1): 67-83. [4] 唐保祥, 任韩. 2类优美图的冠的优美标号[J]. 中山大学学报(自然科学版), 2015, 54(5): 24-27. [5] 魏丽侠, 张坤龙. 几类并图的优美性[J]. 中山大学学报(自然科学版), 2008, 47(3): 10-13. [6] 吴跃生. 图Fn, 4(r1,r2, …,r3n+1) 的交错标号[J]. 中山大学学报(自然科学版), 2016, 55(4): 11-14. [7] YAO B, CHENG H, YAO M, et al. A note on strongly graceful trees [J]. Ars Combinatoria, 2009, 92: 155-169. [8] ZHOU X Q, YAO B, CHEN X E, et al. A proof to the odd-gracefulness of all lobsters [J]. Ars Combinatoria, 2012, 103: 13-18. [9] WANG H Y, YAO B, YAO M. Generalized edge-magic total labellings of models from reseaching networks [J]. Information Sciences, 2014, 279: 460-467. DOI:10.1016/j.ins.2014.03.132. [10] WANG H Y, YAO B, YANG C, et al. Edge-magic total labellings of some network models [J]. Applied Mechanics and Materials, 2013, 347-350: 2752-2757. DOI:10.4028/www.scientific. net/AMM.347-350.2752. [11] WANG H Y, YAO B, YANG C, et al. Labelling properties of models related with complex networks based on constructible structures [J]. Advanced Materials Research, 2013(765/766/767): 1118-1123.DOI:10. 4028/www.scientific.net/AMR.765/766/767.1118. [12] 赵喜杨, 马飞, 姚兵. 一类强优美标号树[J]. 吉林大学学报(理学版), 2016, 54(2): 222-228. Probing (k,d)-edge magic total labellings of trees ZHAOXiyang,YAOBing (College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China) The (k,d)-edgemagicpropertyoftreesisstudied.Byusingtheconnectionbetween(k,d)-gracefullabellingsand(k,d)-edgemagictotallabellingsforgeneratinglargeclassesof(k,d)-edgemagictotaltreesfromsmallergracefultrees,therelationshipbetween(k,d)-gracefullabellingsand(k,d)-edgemagiclabellingsisestablished. graceful labellings; (k,d)-gracefullabellings;edgemagictotallabelling; (k,d)-edgemagictotallabelling 10.13471/j.cnki.acta.snus.2016.06.010 2016-01-11 国家自然科学基金资助项目 (61163054,61363060,61662066) 赵喜杨 (1990年生),女;研究方向:图的标号及染色;通讯作者:姚兵;E-mail:yybb918@163.com O A 0529-6579(2016)06-0067-072 主要结论