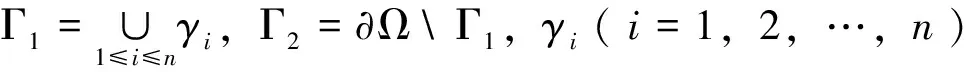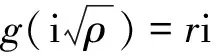Brownian运动首次离开指定边界的概率表达式*
2016-06-05蓝师义
邹 浪,蓝师义
(广西民族大学理学院,广西 南宁 530006)
Brownian运动首次离开指定边界的概率表达式*
邹 浪,蓝师义
(广西民族大学理学院,广西 南宁 530006)
Brownian运动在随机过程与Schramm-Loewner演变(SLE)中扮演着非常重要的角色。首先,利用Brownian运动的性质导出了Brownian运动首次离开指定区域边界的概率表达式,并且通过数值模拟进一步验证了所得到结果的正确性。其次,讨论单连通域内调和测度与Brownian运动首离指定边界概率之间的关系,通过后者的结果给出了前者的具体表达式,同时得到一些相关的结果。
Brownian运动;首离概率;Schramm-Loewner演变;调和测度
Brownian运动是一种重要的随机过程。 国内外许多学者对它进行了大量研究,并得到了许多很好的结果。文[1]研究了在空间任一点出发的Brownian运动在球内停留时间的分布与球面首中时分布;文[2-3]分别研究了Brownian运动首中与末离的联合分布及Brownian关于线性边界的首出时问题,求出了Brownian运动停留在双侧(单侧)逐段线性边界内的概率的分析表达式;文[4-5]研究了Brownian运动首中与末离的联合分布及末遇分布与极大游程等相关内容;文[6-8]分别证明了Brownian运动B[0,1]割点、先驱点、边界的Hausdorff维数分别为3/4,7/4,4/3。同时,Brownian运动的首中时与首出时的分布在很多方面有着重要的应用,例如,在非参数统计、序列分析和财政金融等方面(见文[5,9-10])。另一方面,Schramm[11]于2000年将时间改变的Brownian运动作为驱动函数引入到Loewner微分方程,这导致了一个新的研究领域,即随机Loewner演变(或Schramm-Loewner演变),简称SLE。有关SLE的背景知识和详细内容可参见文[12-13]等。已经知道SLE有很多重要的应用,其中最重要的应用之一是它被成功地用来解决了Brownian运动的相交指数问题(见文[14-16]等)。 此外,也已经证明SLE是许多离散统计物理模型的尺度极限,例如,临界点渗流探索路径收敛于SLE6[17];回路删除随机走动收敛于SLE2与一致生成树Peano路径收敛于SLE8[18];调和探索过程路径与离散Gaussian自由场的回路线收敛于SLE4及FKIsing模型的接口收敛于SLE16/3等[19-21]。

1 Brownian运动及相关结果
首先,简要地介绍一维和二维Brownian运动的定义和一些性质,并导出本文后面将用到的一些相关结果。有关更详细的背景知识可见文[22-23]等。
定义1 一个随机过程Bt称为一个一维的标准Brownian运动, 如果它满足下面条件:
(i)B0=0,a.s.;
(ii) 对所有的s≤t,Bt-Bs是一个均值为0方差为t-s的Gaussian随机变量;
(iii)对所有的s≤t,Bt-Bs独立于σ(Br,r≤s); (iv) 映射t→Bt(ω)几乎肯定是连续的。
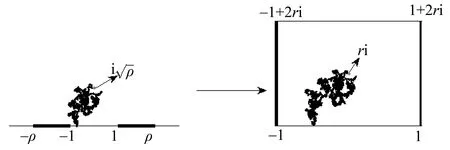
这里σ(Br,r≤s)是关于每一个Br,r≤s都可测的最小σ域。 一个均值为0方差为σ2的Gaussian随机变量X的分布密度函数是由下面公式给出
其中A为任意一个Borel集。

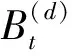
(1)
也就是,式(1)理解为一个d维的标准Brownian运动从x点开始经过时间t到达y的概率密度为p(t,x,y)。
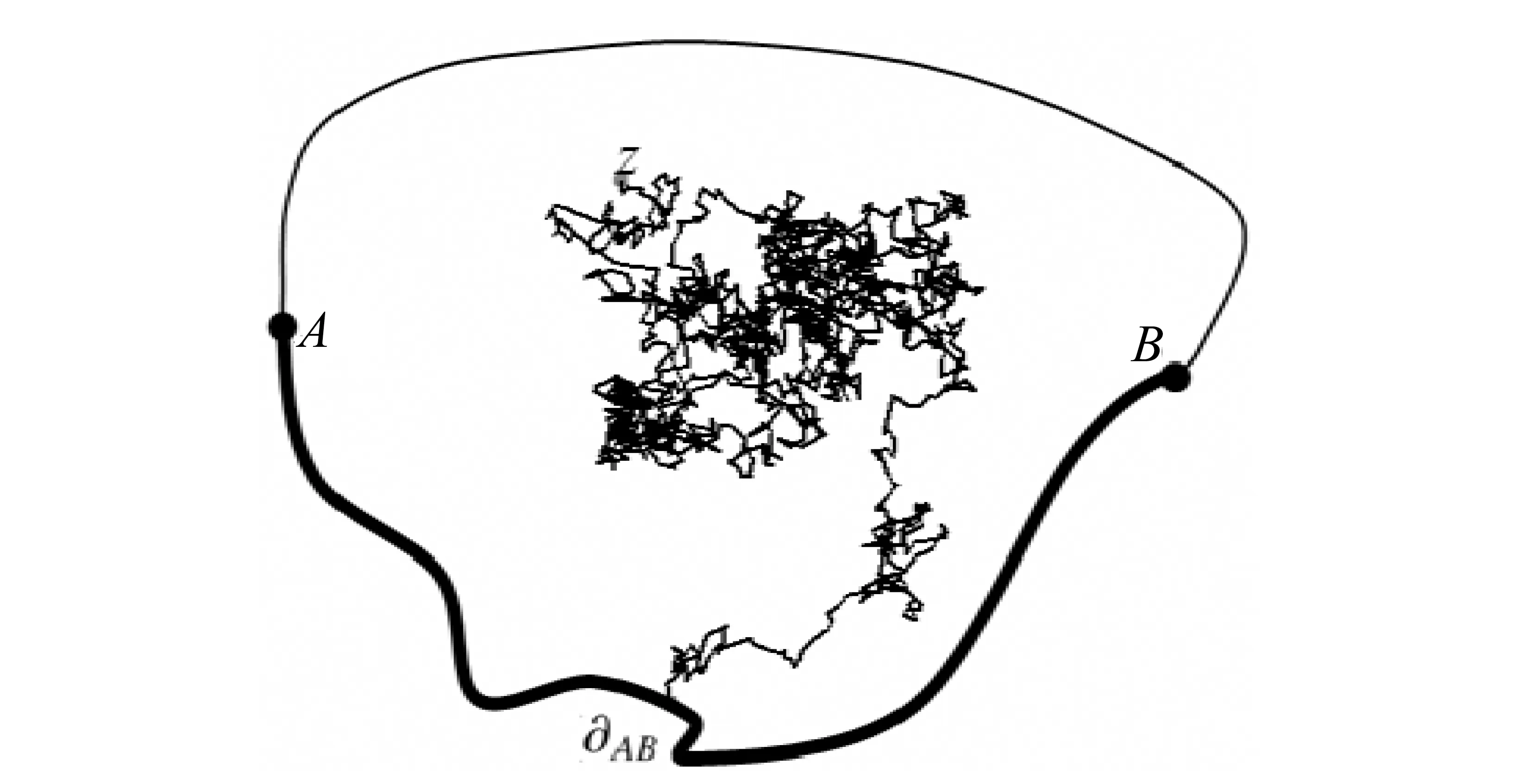
引理1 设X(t)是一个从点x:a 证明 该引理的证明见文[22]中的命题 4.9。 (2) 证明 该引理的证明见文[22]中的定理 3.8。 推论1 设Bt是一个一维的标准Brownian运动。对于给定大于0的实数a,设Ta=inf{t≥0:Bt=a},那么 其中 (3) 当d=1时,容易计算得到 当d≥2时,引入如下d维球坐标变换: x1=rcosφ1,…, xd-1=rsinφ1sinφ2…sinφd-2cosφd-1, xd=rsinφ1sinφ2…sinφd-2sinφd-1 则它的雅可比行列式及积分区域分别为: J=rd-1sind-2φ1sind-3φ2…sinφd-2和0≤r<∞,0≤φ1,φ2,…,φd-2≤π,0≤φd-1≤2π 于是式(3)就变成 (4) 这里 为一个只依赖于d的常数。 在式(4)中令r2/(2t)=x,则得到 (5) (6) (7) (8) 因此,由式(6)与式(8)得到 也就是,式(5)成立,这就完成了该定理证明。 基于第1节的结果,将讨论d维Brownian运动第1次离开几种类型单连通区域指定边界的概率估计,导出了它们具体表达式。并通过数值模拟验证了所得到结果的正确性。 (9) 图1 一个二维Brownian运动从单连通域Ω的一个指定边界∂AB首次离开的情形Fig.1 A 2D-Brownian motion exits first a simply connected domain Ω at a prescribed boundary ∂AB (10) 这里,φ是一个从Ω到带形区域Sπ={z∈C:0 下面讨论区域Ω的4种特殊情形: (i) 当Ω是平面C内的一个半径为r的圆盘域D时,见图2(a)。 (11) (ii) 当Ω是平面C内的一个弓形域Bθ时,见图2(b)。 (12) (iii) 当Ω是第一象限域C1={z∈C:Imz>0,Rez>0}时,见图2(c)。 (13) 图2 Brownian运动分别从4个不同区域的指定边界首次离开的情形Fig.2 The Brownian motions exit first four distinct regions at the prescribed boundary parts, respectively 表1 二维Brownian运动第一次碰到Bπ的边界∂π的模拟概率与理论概率 从表1中可以看出,随机模拟概率与理论概率非常接近,这验证了我们结论的正确性。 定理6 设Ω⊂C是由一条简单闭曲线围成的单连通区域且其边界分为相连的两部分∂1,∂2。设ω(z)为Ω中z处∂1的调和测度,若φ是一个从Ω到带形区域Sπ的共形映射且满足φ(∂1)=Rπ,那么ω(z)可表示为 (14) (15) 这里的φi为Ω到Sπ的共形映射且满足φi(γi) =Rπ,i=1,2,…,n。 (16) 图3 上半平面H中一个二维Brownian运动样本共形映射到一个矩形区域的情形Fig.3 A sample of 2D Brownian motion in upper half plane H was conformally mapped onto a rectangular domain (17) 这里ρ=h(r)。也就是,式(16)成立,定理7证明完成。 [1] 尹传存, 吴荣.Brown运动关于球及球面的若干问题[J]. 中国科学, 1996, 26(5): 412-422. [2] 王梓坤. 布朗运动首中与末离的联合分布[J]. 科学通报, 1994, 13(13): 1168-1173. [3] 徐润, 吕玉华. 标准布朗运动关于线性边界通过概率[J].JournalofMathematicalResearchwithApplications, 2005, 25(4): 709-715. [4] 王梓坤. 布朗运动的末遇分布及极大游程[J]. 中国科学, 1980, 10(10): 933-940. [5]WANGZK.ThejointdistributionsoffirsthittingandlastexitforBrownianmotion[J].ChineseSciBull, 1995, 40(6): 451-457. [6]LAWLERGF.HausdorffdimensionofcutpointsforBrownianmotion[J].ElectronicJournalofProbability, 1996, 1(2): 1-20. [7]LAWLERGF.GeometricandfractalpropertiesofBrownianmotionandrandomwalkpathsintwoandthreedimensions[J].BolyaiMathSocStudies, 1998: 219-258. [8]LAWLERGF.ThedimensionofthefrontierofplanarBrownianmotion[J].ElectronCommProbab, 1996, 306(5): 29-47. [9]JOHNSONRA.Sequentialnonparametrics:invarianceprinciplesandstatisticalinference[J].Technometrics, 1983, 25(25): 214-215. [10]SIEGMUNDD.Sequentialanalysis:testsandconfidenceintervals[M].Berlin:Springer-Verlag, 1985. [11]SCHRAMMO.Scalinglimitsofloop-erasedrandomwalksanduniformanduniformspanningtrees[J].IsraelJMath, 2000, 118(1): 221-288. [12]LAWLERGF.Conformallyinvariantprocessesintheplane[J].MathematicalSurveys&Monographs, 2005, 114: 305-351. [13]WERNERW.RandomplanarcurvesandSchramm-Loewnerevolutions[J].InLecturesonProbabilityTheoryandStatistics, 2003, 1840: 107-195. [14]LAWLERGF,SCHRAMMO,WERNERW.ValuesofBrownianintersectionexponentsI:Half-planeexponents[J].ActaMathematica, 2001, 187(2): 237-273. [15]LAWLERGF,OSCHRAMMO,WERNERW.ValuesofBrownianintersectionexponentsII:Planeexponents[J].ActaMathematica, 2001, 187(2): 275-308. [16]LAWLERGF,SCHRAMMO,WERNERW.ValuesofBrownianintersectionexponentsIII:two-sidedexponents[J].AnnIntHenriPoincaré, 2002, 38: 109-123. [17]SMIRNOVS.Criticalpercolationintheplane:conformalinvariance,Cardy’sformula,scalinglimits[J].ComptesRendusde1AcadémiedesSciencesSeriesIMathematics, 2001, 333(3): 239-244. [18]LAWLERGF,SCHRAMMO,WERNERW.Conformalinvarianceofplanarloop-erasedrandomwalksanduniformspanningtrees[J].AnnalsofProbability, 2002, 32(1B): 939-995. [19]SCHRAMMO,SHEFFIELDS.TheharmonicexploreranditsconvergencetoSLE(4) [J].AnnalsofProbability, 2003, 33(6): 2127-2148. [20]SCHRAMMO,SHEFFIELDS.Contourlinesofthetwo-dimensionaldiscreteGaussianfreefield[J].ActaMathematica, 2009, 202(1): 21-137. [21]SMIRNOVS.Conformalinvarianceinrandomclustermodels.I.HolmorphicfermionsintheIsingmodel[J].AnnofMath, 2010, 172(2): 1435-1467. [22]BASSRF.Probabilistictechniquesinanalysis[M].NewYork:SpringerScienceandBusinessMedia, 1995. [23]REVUZD,YORM.ContinuousMartingalesandBrownianmotion,thirdedition[M].Berlin:Springer-Verlag, 1999. [24]KAGERW,NIENHUISB.AguidetostochasticLownerevolutionanditsapplications[J].JournalofStatisticalPhysics, 2004,115(5/6): 1149-1229. [25]PRUDNIKOVAP,BRYCHKOVYA,ARICHEVOI.Integralsandseries,Vol2:specialfunctions[M].NewYork:GordonandBreachSciencePublishers, 1990. The probability expressions of first exit for Brownian motions at prescribed boundary parts of regions ZOULang,LANShiyi (College of Science, Guangxi University for Nationalities, Nanning 530006, China) Brownian motion plays a very important role in both stochastic process and Schramm Loewner Evolution (SLE). Firstly, by using the properties of Brownian motions, it is derived that the probability expressions of Brownian motion exiting first at prescribed boundary parts of regions. The correctness of the obtained results is verified by numerical simulations. Secondly, the relationship between harmonic measure and probability of Brownian motion exiting first a simply connected domain at the specified boundary is discussed. The probability formulas of the former are derived by using the results of the latter. In addition, some other related results are obtained. Brownian motion; probability of first exit; Schramm-Loewner Evolution; harmonic measure 10.13471/j.cnki.acta.snus.2016.06.006 2015-12-09 国家自然科学基金资助项目(11161004,11661011);广西自然科学基金资助项目(2013GXNSFAA019015,2016GXNSFAA380099);广西民族大学研究生创新计划资助项目(gxun-chxs2015093) 邹浪 (1989年生),男;研究方向:随机Loewner演变;通讯作者:蓝师义;E-mail:shiyilan05@sina.com O211 A 0529-6579(2016)06-0044-09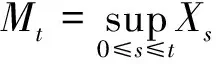
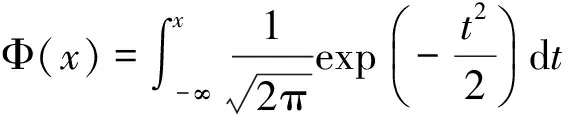

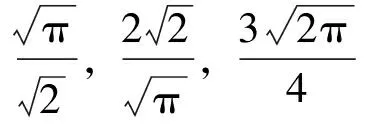


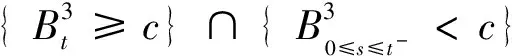
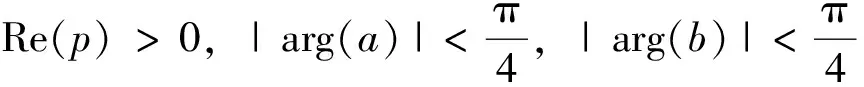
2 Brownian运动首次离开指定区域边界的概率公式
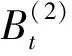
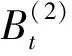

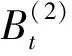
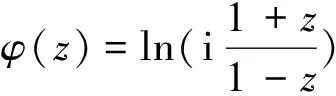
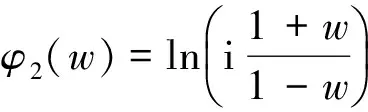
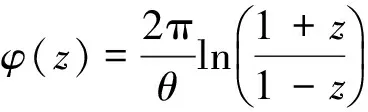
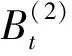
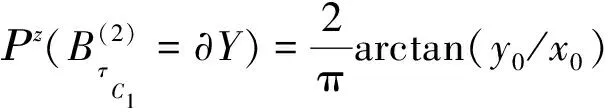
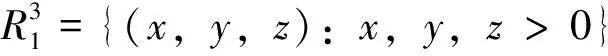
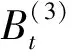
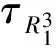
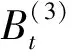

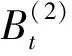
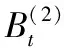
3 调和测度与首离概率的关系