On the characteristic polynomials of graphs with nullity n-4

, ,

(1. School of Mathematics and Statistics, Qinghai Nationalities University, Xining 810007, China;2. Department of Mathematics, Central South University, Changsha 410083, China)

On the characteristic polynomials of graphs with nullityn-4

WUTingzeng1,FENGLihua2,MAHaicheng1

(1. School of Mathematics and Statistics, Qinghai Nationalities University, Xining 810007, China;2. Department of Mathematics, Central South University, Changsha 410083, China)

The nullity of a graph is the multiplicity of zeroes in its adjacency spectrum. And the nullity of a graphGwithnverticesequalstonminustherankofadjacencymatrixofG.Thecharacteristicpolynomialsofgraphswithnullityn-4iscomputed.Inparticular,itisshownthatsomegraphswithnullityn-4aredeterminedbytheirspectra.Andsomepairsofcospectralgraphswithnullityn-4arepresented.

characteristic polynomial; rank; nullity; cospectral graphs

1 Introduction

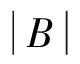
TheadjacencymatrixofGisdenotedbyA(G).ThecharacteristicpolynomialofagraphG,bydefinition,is

whereIistheidentitymatrixofordern.

ThespectrumofGconsistsoftheeigenvaluestogetherwiththeirmultiplicitiesofA(G).Twographsaresaidtobecospectralif they share the same spectrum or characteristic polynomial.

A graph is said to bedeterminedbythespectrum(DS for short) if there is no other non-isomorphic graph with the same spectrum. The nullity ofG,denotedbyη(G),isthemultiplicityofzeroesinthespectrumofG.Letr(G)betherankofA(G).Obviously,η(G)=n-r(G).Whenη(G)=0,thegraphGiscallednonsingular.

TheproblemcharacterizingallgraphsGwithη(G)>0isofgreatinterestinbothchemistryandmathematics.ForabipartitegraphGwhichcorrespondstoanalteranthydrocarboninchemistry,ifη(G)>0,itisindicatedthatthecorrespondingmoleculeisunstable.Thenullityofagraphisalsomeaningfulinmathematicssinceitisrelatedtothesingularityofadjacentmatrix.Theproblemhasnotyetbeensolvedcompletely.Anditreceivedalotofattentionfromresearchersinrecentyears,see[2-3].Herewehighlighttworesultswhichinvolveextremalnullityofgraphs.Thatis,ChengandLiu[4]characterizedthegraphswhosenullityreachtheupperboundsn-2andn-3.Changetal. [5-6]masterlyusedthedefinitionofmultiplicationofvertices(seep.53of[7])tocharacterizeallconnectedgraphswithrank4or5.Moreinformationsee[8-9].

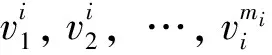
BythedefinitionofG∘m[m1,m2,…,mn],wecanobtainsomeprimarypropertiesaboutthestructureofG∘m as follows.

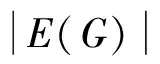
Property 3 For any triangle inG∘m, there exactly exists a complete 3-partite induced subgraph obtained by multiplying vertices on a triangle inGwhichcontainsit.Then

whereuvwdenotesatriangleinG,andthesumistakenoveralltrianglesinG.

Property4Every4-cycleinG∘m must be contained in an induced subgraph obtained by multiplying every vertex on an edge, oneP3oroneC4inG.Directcomputationyields

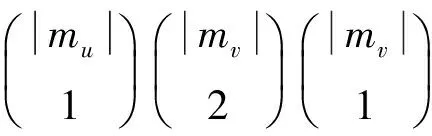
wherethefirstsumistakenoveralledgesinG,thesecondsumistakenoverallP3’sinG,andthethirdsumistakenoverallC4’sinG.

Thispaperisorganizedasfollows.InSection2,wepresentsomelemmasandcharacterizeallgraphswithnullityn-4.InSection3,wecomputethecharacteristicpolynomialsofgraphswithnullityn-4.InSection4,weinvestigatewhichgraphswithnullityn-4areDS.Precisely,weshowthattwoclassesofregulargraphsandoneclassofnon-bipartitegraphsareDS.Andwepresentsomepairsofcospectralbipartitegraphs.

2 Preliminaries

Inthissection,wewillpresentsomeresultswhichplayakeyroleintheproofsofthemaintheorems.

Lemma 1[1]LetGbeagraphwithpverticesandqedges,andlet(d1,d2,…,dp)bethedegreesequenceofG.ThecoefficientsofthecharacteristicpolynomialofagraphGsatisfy:

(i)a0=1;

(ii)a1=0;

(iii)a2=-q;

(iv)a3=-2c3(G);

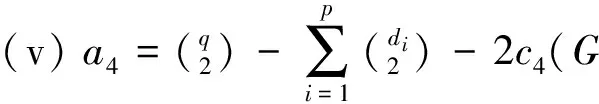
Lemma 2[10]LetGbeagraph.Fortheadjacencymatrix,thefollowingcanbeobtainedfromthespectrum.

(i) The number of vertices.

(ii) The number of edges.

(iii) WhetherGisregular.

(iv) WhetherGisregularwithanyfixedgirth.

(v) The number of closed walk of any length.

(vi) WhetherGisbipartite.

Theorem 1[4]Suppose thatGisasimplegraphonnverticesandn≥2.Thenη(G)=n-2ifandonlyifGisisomorphictoKn1,n2∪kK1,wheren1+n2+k=n,n1andn2>0,andk≥0.

Theorem 2[5]LetGbeaconnectedgraph.Thenr(G)=4ifandonlyifG∈M(G1,G2,G3,G4,G5,G6,G7,G8),whereGi(i=1,2,…,8)isdepictedinFig.1.

CombiningTheorems1and2,wecanobtainthefollowingresult.

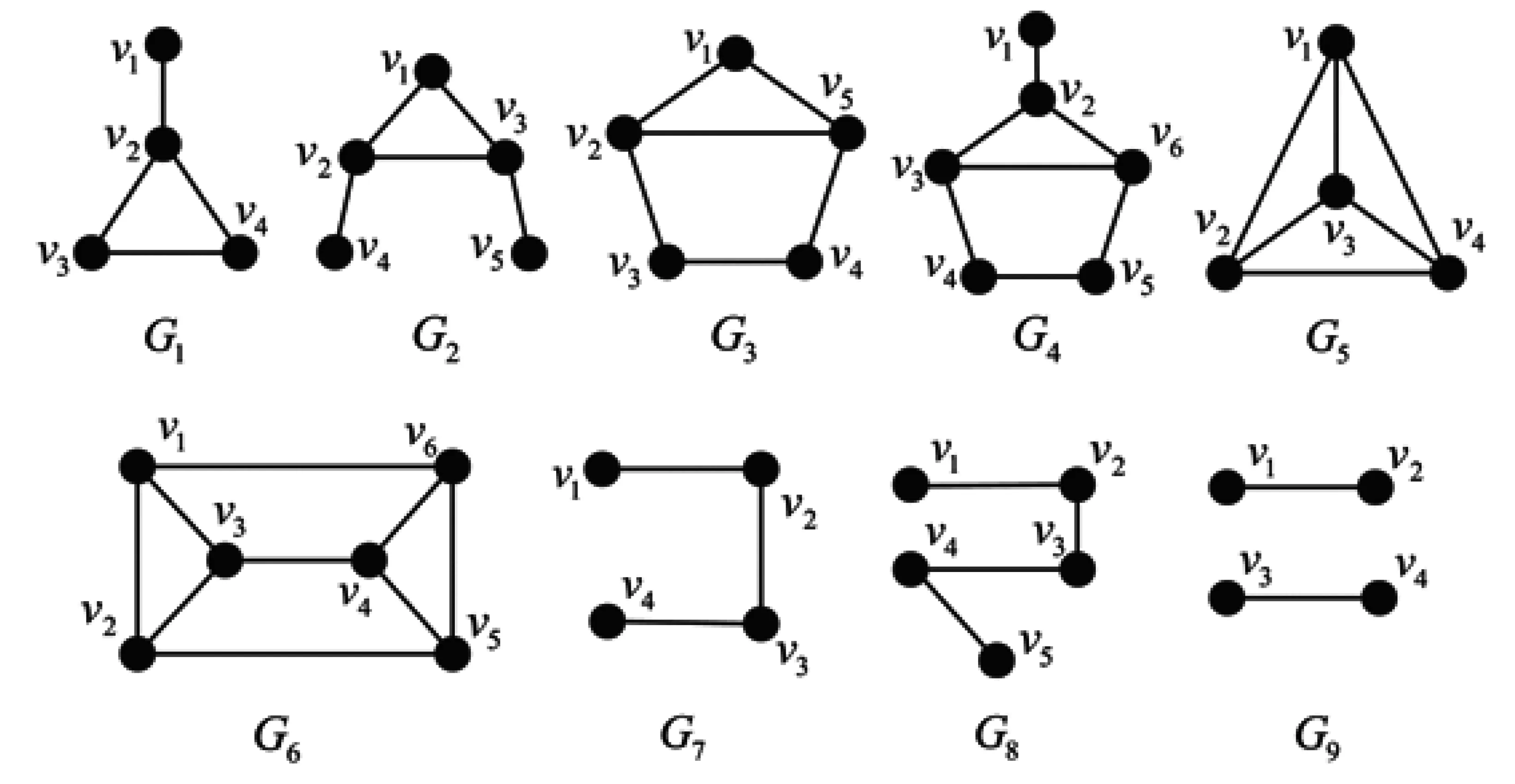
Fig.1 The graphs G1,G2,G3,G4,G5,G6,G7,G8,G9

3 The characteristic polynomials of graphs with nullity n-4

Inthissection,wewillcomputethecharacteristicpolynomialsofgraphswithrank4.

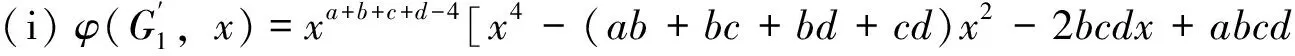
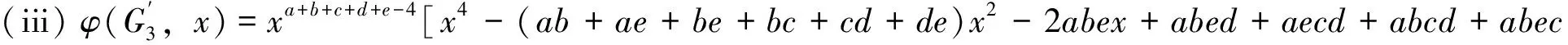
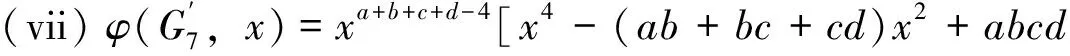
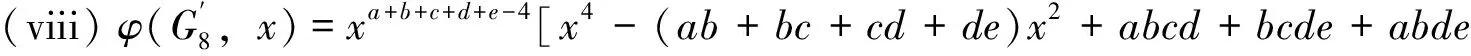
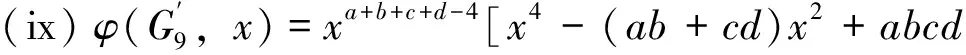
Proof

cd)xa+b+c+d-2-2bcdxa+b+c+d-3+abcdxa+b+c+d-4

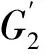
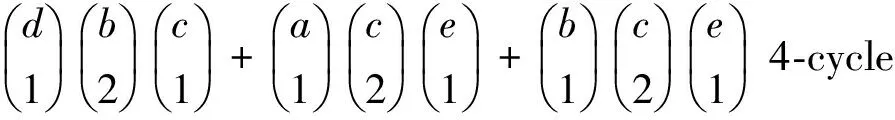
bd+ce)x2-2abcx+abdc+abec+dbec]

xa+b+c+d+e-4[x4-(ab+ae+be+bc+cd+de)·

x2-2abex+abed+adec+abcd+abec]

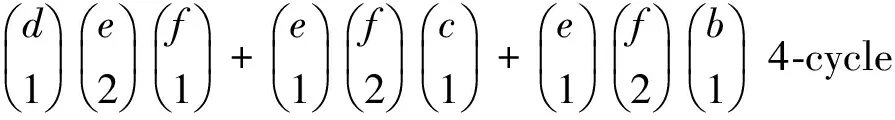
cf+cd+de+ef)x2-2bcfx+abed+

abcd+bdec+abcf+abef+bcef+fbcd+fbed]

3abcd4-cycles.ByLemma1,wehave

bc+bd+cd)x2-

2(abc+abd+acd+bcd)x-3abcd]

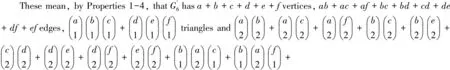
abef+acdf+bcde4-cycles.ByLemma1,wehave

[x4-(ab+ac+af+bc+be+cd+

df+de+fe)x2-2(abc+def)x+abed+

abdf+acbe+aced+acef+afed+abcd+fcde+

abcf+bcef+fbcd+fbed]

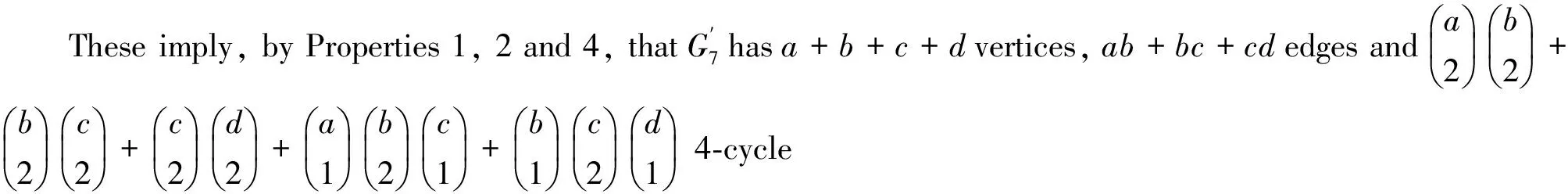
[x4-(ab+bc+cd)x2+abcd]

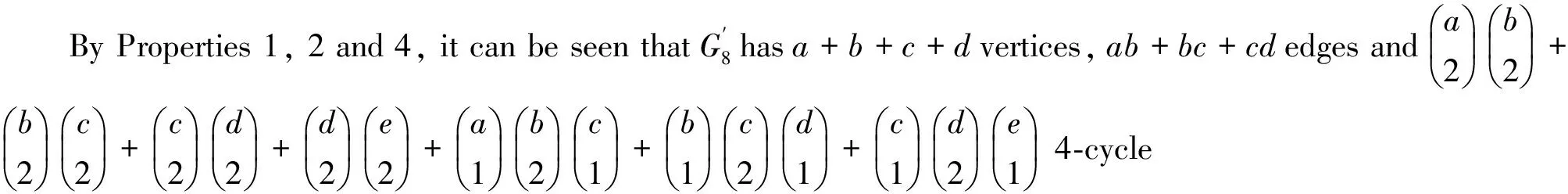
[x4-(ab+bc+cd+ed)x2+abcd]

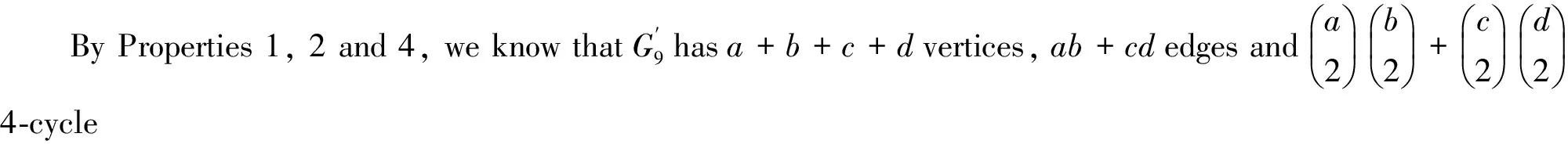
[x4-(ab+cd)x2+abcd]

Bytheaboveargument,weobtainthedesiredresult.

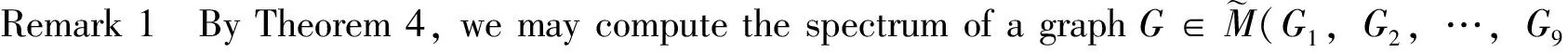
4 The spectral characterization of graphs with nullity n-4

MaandRen[15]investigatedwhichkindofcompletemultipartitegraphisDSsinceitiswellknownthatnotallcompletemultipartitegraphsareDS.Andtheyprovedthefollowingresults.

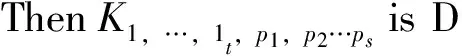
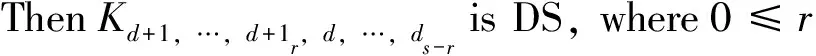
ByTheorems5and6,weobtaindirectlyacorollaryasfollows.

Theorem 7

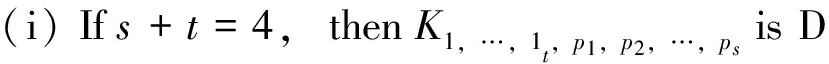
(ii) The complete regular 4-partite graph is DS.

Additionally, by the definition ofG5。 m[m1,m2,m3,m4],wenotethatG5∘m is a complete 4-partite graphs. Observing Theorem 4, it is easy to see that only the fifth coefficient of characteristic polynomial ofG5∘m is negative, which implies that the following proposition.

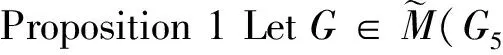
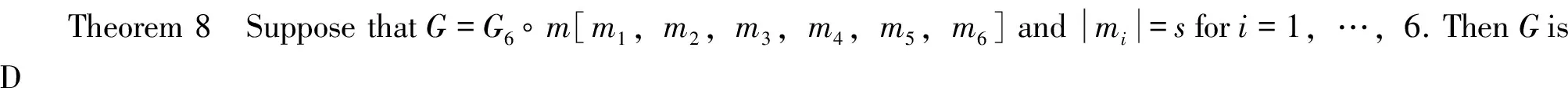
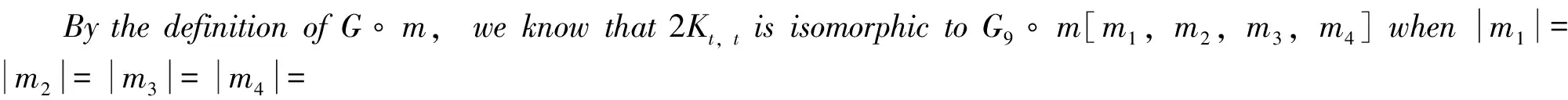
Theorem 9 2Kt,tisDS.

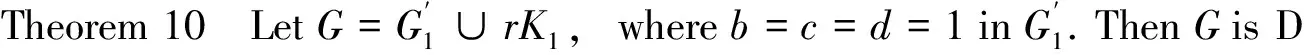
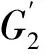
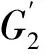
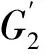
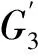
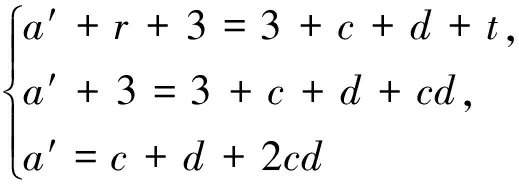
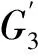
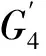
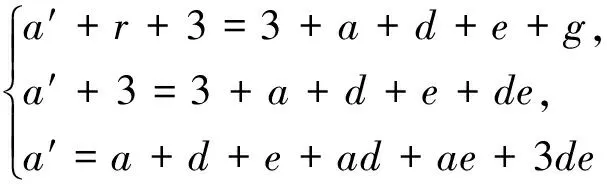
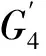
Fromtheargumentabove,weobtainthatGisDS.

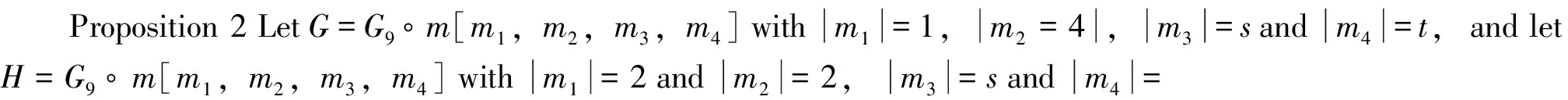
Proof. By Theorem 4 (vii) and (viii), we obtain that

Therefore,G∪kK1andH∪kK1arecospectral,wherea,k≥0.

5 Conclusion

[1] BIGGS N. Algebraic graph theory [M]. Cambridge: Cambridge University Press, 1993.

[2] BOROVICANIN B, GUTMAN I. Nullity of graphs [C]. Applications of Graph Spectra, Math Inst. Belgrade, 2009:107-122.

[3] GUTMAN I, BOROVICANIN B. Nullity of graphs: an updated survey [C]. Selected Topics on Applications of Graph Spectra, Math Inst. Belgrade, 2011: 137-154.

[4] CHENG B, LIU B. On the nullity of graphs [J]. Electron J Linear Algebra Ela, 2007, 16: 60-67.

[5] CHANG G, HUANG L, YEH H. A characterization of graphs with rank 4 [J]. Linear Algebra Appl, 2011, 434(8): 1793-1798.

[6] CHANG G, HUANG L, YEH H. A characterization of graphs with rank 5 [J]. Linear Algebra Appl, 2012, 436(11): 4241-4250.

[7] GOLUMBIC M. Algorithmic graph theory and perfect graphs [M]. Amsterdam: North-Holland Publishing Co, 2004.

[8] WANG X, ZHAO X, YAO B. Spanning trees of totally edge-growing network models [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(1): 48-53.

[9] TANG B, REN H. The number of perfect matching in two types of 3-regular graph [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2014, 53 (5): 54-58.

[10] van DAM E, HAEMERS W. Which graphs are determined by their spectrum? [J]. Linear Algebra Appl, 2003, 373: 241-272.

[11] van DAM E, HAEMERS W. Developments on spectral characterizations of graphs [J]. Discrete Math, 2009, 309: 576-586.

[12] CAMARA M, HAEMERS W. Spectral characterizations of almost complete graphs [J]. Discrete Appl Math, 2014, 176: 19-23.

[13] LIU F, HUANG Q, LAI H. Note on the spectral characterization of some cubic graphs with maximum number of triangles [J]. Linear Algebra Appl, 2013, 438(3): 1393-1397.

[14] ZHANG X, ZHANG H. Some graphs determined by their spectra [J]. Linear Algebra Appl, 2009, 431(9): 1443-1454.

[15] MA H, REN H. On the spectral characterization of the union of complete multipartite graph and some isolated vertices [J]. Discrete Math, 2010, 310: 3648-3652.

2015-11-28

国家自然基金资助项目 (11101245, 11271208, 11301302, 11561056)；青海省自然基金资助项目(2016-ZJ-947Q)；山东省自然基金资助项目(BS2013SF009)；中南大学数学与交叉科学项目资助项目；青海民族大学自然科学基金资助项目(2015XJZ12)

吴廷增(1978年生)，男；研究方向：数学化学、图的匹配理论和计算机网络；E-mail:mathtzwu@163.com

零度为n-4的图的特征多项式*

吴廷增1, 冯立华2, 马海成1

(1. 青海民族大学数学与统计学院, 青海 西宁 810007;2. 中南大学数学系, 湖南 长沙 410083)

图的零度是指图的邻接谱中零特征根的重数。显然,n个顶点的图G的零度等于n减去其邻接矩阵的秩。计算了零度为n-4的所有图的特征多项式。特别地, 证明了许多零度为n-4的图是谱唯一确定的, 并构造了许多对零度为n-4的同谱图。

特征多项式; 秩; 零度; 同谱图

O157.6；O

A

0529-6579(2016)06-0057-07

10.13471/j.cnki.acta.snus.2016.06.008