空速投放的机载飞行器初始地速和姿态确定方法

梁 卓，刘 娟，潘彦鹏，陈旭东，周国峰



空速投放的机载飞行器初始地速和姿态确定方法

梁 卓，刘 娟，潘彦鹏，陈旭东，周国峰

（中国运载火箭技术研究院，北京，100076）

对于空速投放的机载飞行器，一方面由于弹道设计采用的模型基于地速，需将载机给出的投放初始空速转换成初始地速；另一方面，载机投放飞行器时要保持稳定平飞，遇到侧风干扰时，需进行偏流角修正，以保证载机沿着理论航迹线飞行。根据空速投放的机载飞行器特点，从载机速度、姿态的定义出发，基于侧风干扰下的载机偏流角修正思想，推导并建立投放时刻飞行器初始地速和姿态的计算模型。该模型具有简单实用、便于工程实现的特点，可广泛应用于机载飞行器的投放初始参数解算。

空速投放；机载飞行器；偏流角修正；初始地速和姿态

0 引 言

机载飞行器只有进入投弹窗口时，才允许发射，投弹窗口主要由载机的投放速度、投放姿态及投放区域构成。投弹相关参数是飞行器离架自主飞行的初始条件，其中投放速度通常包括空速投放和地速投放两种形式[1~3]，投弹区域一般是关于投放速度和投放高度的函数。投放初始姿态信息一部分可由载机导航数据直接获取，另一部分信息需要计算得到。目前，对于机载飞行器，可查阅的关于投弹窗口相关的文献主要集中介绍了不同类型飞行器投放窗口覆盖区域的计算方法建模及其对窗口范围的影响因素分析，而对投放瞬间初始参数的确定方法尚无系统介绍。

本文主要针对空速投放的机载飞行器特点，从载机速度、姿态的定义出发，基于侧风干扰下载机偏流角修正思路，推导并建立了投放时刻飞行器初始地速和姿态的计算模型，可为基于空速投放的机载飞行器发射初始参数的解算提供依据。

1 载机相关参数定义

1.1 载机速度的定义

载机速度主要包括真空速和地速两种形式。真空速是载机相对气流的运动速度，地速是载机相对地面的运动速度。真空速、地速和风速之间构成矢量三角形。

1.2 载机坐标系定义

2 载机偏流角修正方法

载机在空中飞行时，不可避免地存在风干扰，在侧风条件下，如果不进行修正，载机将随风漂移，产生偏流角（即地速与空速之间的夹角），导致地速矢量方向偏离目标航迹。因此，载机在侧风中飞行，为保持沿着理论航迹飞行，需对偏流进行修正。偏流修正方法是通过操纵载机向侧风方向改变一个航向角，航向角大小与偏流角大小相同，确保载机机轴指向与真空速在水平面内的投影方向一致[6]。

3 初始地速和姿态的计算方法

3.1 初始地速计算

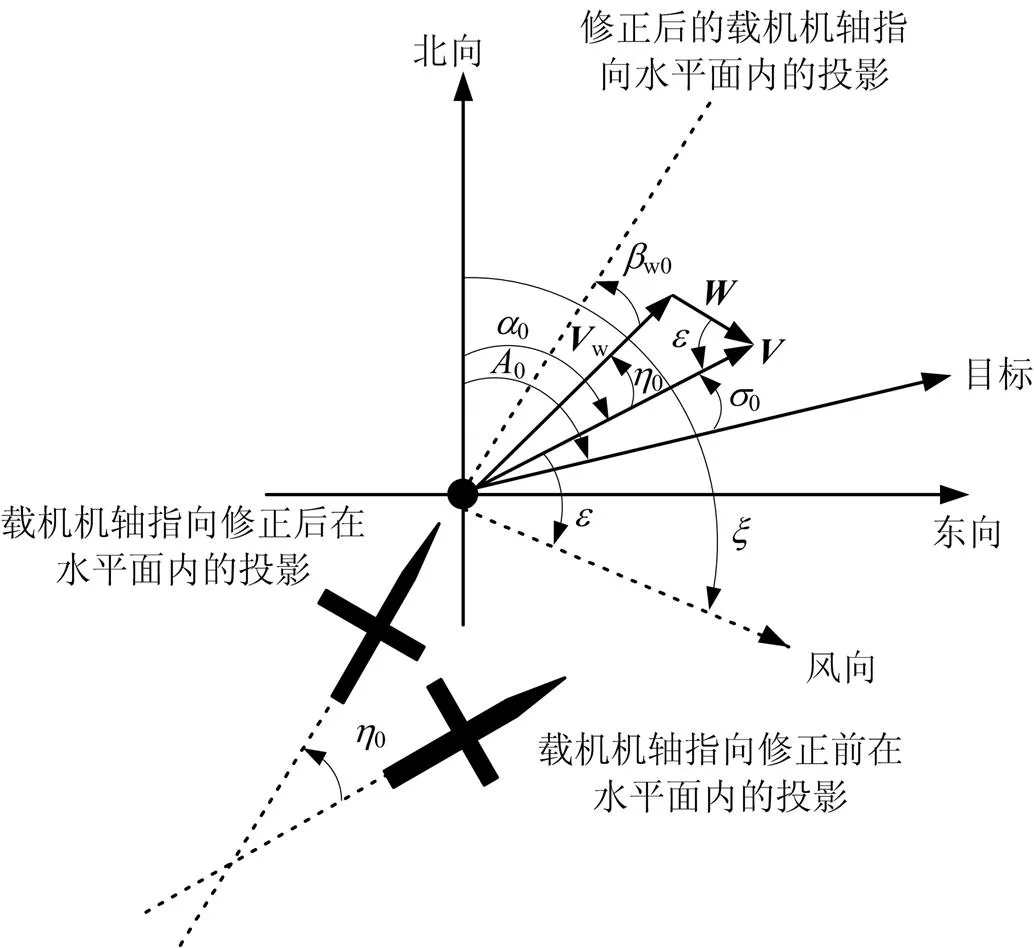
图1 真空速、地速和风速在水平面内的几何关系

（1）

根据图1中的几何关系可以推导出如下公式：

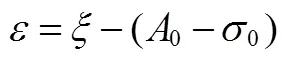
若已知真空速和风速，求地速，计算方法如下：

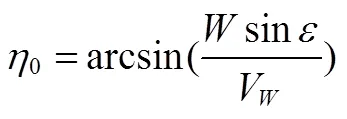
由余弦定理得：

（4）

3.2 初始姿态计算

计算实际航迹角与理论航迹角时，将地球视为不旋转圆球体考虑，采用球面三角计算公式进行射击方位角及射程角的计算。计算方法如下：

实际航迹角：

理论航迹角：

（6）

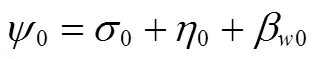
4 结束语

本文针对空速投放的机载飞行器特点，从载机速度、姿态的定义出发，基于侧风干扰下载机偏流角修正思路，推导并建立了投放时刻飞行器初始地速和姿态的计算模型。该模型简单实用，易于工程应用，为空速投放的各类机载飞行器发射初始参数的确定提供了有效方法。

[1] 梁卓, 管雪元, 孙瑞胜, 等. 基于复合制导律的“惯性/卫星”制导炸弹投放域计算[J]. 弹道学报, 2007, 19(3): 27-30.

[2] 陈绍炜, 龚诚. 无推力可控弹可达域和投放域计算[J]. 系统工程与电子技术, 2001, 23(12): 28-30.

[3] Dohrmann C K, Eislser G R, Robinett R D. Dynamic programming approach for bumout-to-apogee guidance of preci-sion munitions[J]. J of Guidance Control and Dynamics, 1996, 19(2): 340-346.

[4] 谢奇峰, 冯金富, 于雷, 等. 激光制导炸弹投放域分析[J]. 火力与指挥控制, 2006, 31(5): 57 -61.

[5] 雷科, 林忠贤. 制导炸弹攻击区拟合算法研究[J]. 电光与控制, 2013, 20(2): 85-88.

[6] 匡江红, 王秉良, 吕鸿雁. 飞机飞行力学[M]. 北京: 清华大学出版社, 2012.

A Researching Method on Calibrating Initial Speed and Attitude for Airborne Vehicles Launched with Air-Speed

Liang Zhuo, Liu Juan, Pan Yan-peng, Chen Xu-dong, Zhou Guo-feng

(China Academy of Launch Vehicle Technology, Beijing, 100076)

For the airborne vehicles launched with air-Speed, on one hand, its trajectory simulation model is based on speed, so initial speed is derived from the initial air-speed. On the other hand, airborne vehicles should be launched under the state of steady level flight, thus the drift angle is needed to be modified against side wind disturbance in order to keep trajectories, Considering the characteristics of airborne vehicles launched with air-Speed, on the basis of definitions of plane’s speed and attitude, a mathematic model of calculating initial speed and attitude are established. Furthermore, it is simple and practical, so it could be commendably applied in the engineering field for its perspective value.

Air-speed launching; Airborne vehicles; Drift angle adjustment; Initial speed and attitude

1004-7182(2016)02-0059-03

10.7654/j.issn.1004-7182.20160213

V249.121

A

2014-12-01；

2015-01-05

梁 卓（1982-），男，高级工程师，主要研究方向为导航、制导与控制技术及仿真