基于转动矩阵法的火箭上面级机动程序角设计

王传魁，周文勇，陈 益，张利宾，解永锋



基于转动矩阵法的火箭上面级机动程序角设计

王传魁，周文勇，陈 益，张利宾，解永锋

（北京宇航系统工程研究所，北京，100076）

提出一种运载火箭上面级机动程序角设计方法。采用多个参考坐标系之间的转换关系，计算转动矩阵，最终求解出上面级的飞行程序角。经过数值仿真，验证了本方法的可行性。火箭上面级作为基础级火箭和卫星等有效载荷之间的纽带可以采用此方法进行轨道设计以满足不同有效载荷对轨道参数的要求。

转动矩阵；轨道机动；程序角

0 引 言

在运载火箭发射轨道设计过程中，为了达到有效载荷所要求的预定轨道，程序角一般从发射起至转弯前保持不变，转弯段程序角按照不同转弯方式根据经验公式计算，其它飞行阶段采用直接对程序角进行线性化处理，利用主机点火来满足对轨道设计要求。而上面级一般利用运载火箭基础级预先进入过渡轨道，然后选择合适的时机点火进行轨道机动，以改变轨道。

经过长时间的飞行，火箭上面级入轨后在发射惯性系下程序角的3个方向与轨道参数改变不能够进行一一对应关系的转化，相互耦合，较难实现变轨。由于飞行时间较长，上面级机动方向的选择较为困难，如果仍然在发射惯性系对程序角进行设计就变得较为抽象，选择计算初值成为一大难点。因此借鉴卫星变轨设计方法，在轨道系下做机动方向调整，先计算上面级相对轨道系的姿态角，然后进行坐标转换计算出要求的程序角，完成程序角的设计。

1 坐标系定义及转换关系

1.1 坐标系定义

b）发射坐标系。

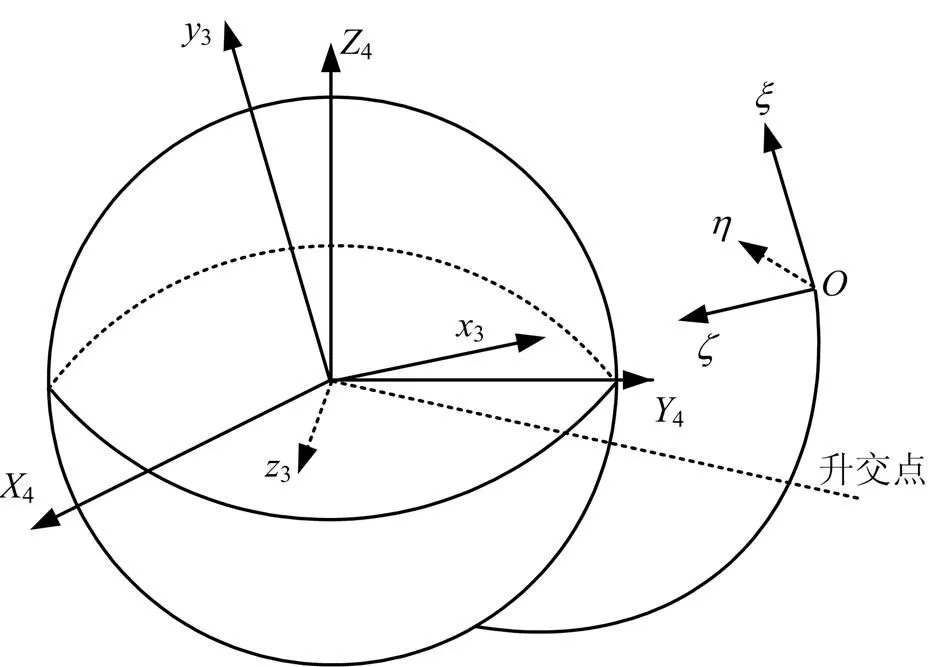
图1 坐标系示意图

1.2 欧拉角定义

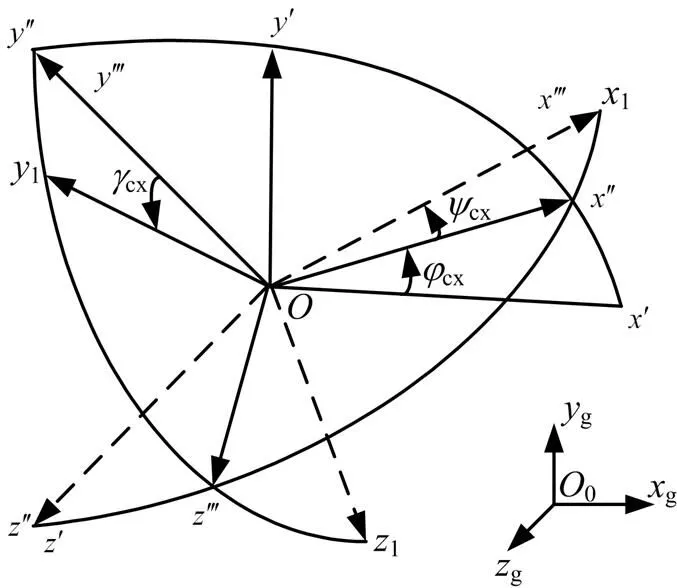
图2 程序角定义示意

1.3 坐标转换关系

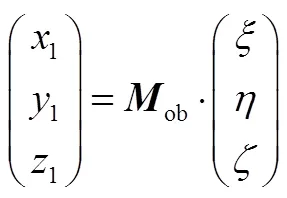
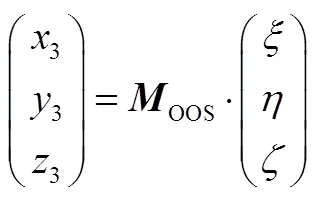
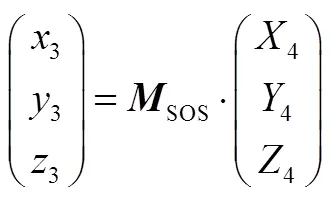
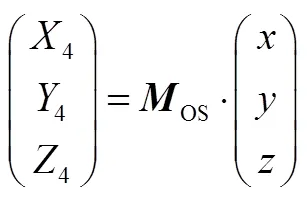
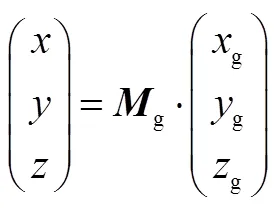
根据程序角定义，将发射惯性系原点平移至上面级体系原点后，再依次绕新坐标系，，轴旋转、，角，即可与本体系重合（见图2）。

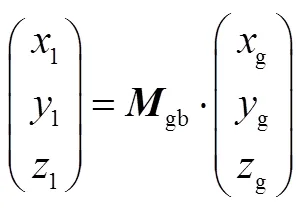
2 程序角的计算

如果想求解本体系推力矢量转换到发射惯性系下，需要先转换到轨道系下；然后由轨道系转换到地心轨道系下；再由地心轨道系下转换到地心系下；再由地心系转换到发射系；最后由发射系转换到发射惯性系。因此可以将转换矩阵按照转换顺序逆向做乘积就可以得到发惯系到本体系的转换矩阵，如下所示：

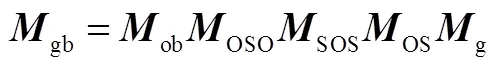
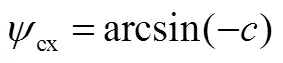
3 机动程序角设计

首先定义3个矢量方向，将航天器地心矢量方向定义为径向，由地心指向航天器的方向定义为正径向；将沿航天器轨道切向方向定义为切向，沿航天器飞行速度方向定义为正切向；将过航天器与轨道面垂直的方向定义为法向，其中正法向由右手螺旋定则确定（与轨道动量距方向相同），如图3所示。不难发现，正切向与轨道系轴指向接近，正法向与轨道系y轴指向相反，正径向与轨道系轴指向相反。

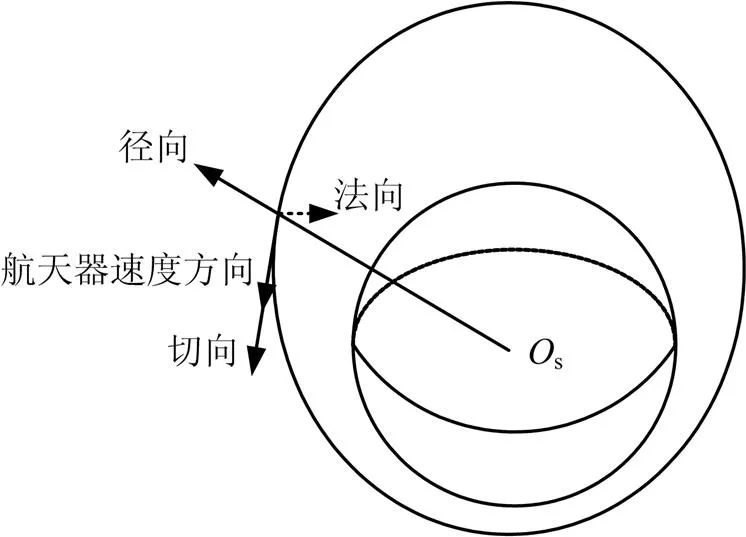
图3 矢量定义示意

从上述定义和描述不难看出，沿轨道切向施加速度脉冲，能够改变轨道的速度；沿轨道法向施加速度脉冲，能够改变轨道平面的位置，对轨道的速度和形状不会产生明显影响。上述两种变化都是工程应用中经常用到的轨道机动方式。

在实际工程中施加速度脉冲不能实现，只能靠发动机的持续工作产生推力来达到相似的效果。因此经常通过轨道拱点（近地点或远地点）附近沿轨道正切向点火工作，来实现轨道速度的增加，增大轨道半长轴，此时上面级本体坐标系与轨道坐标系重合，可以采用相对轨道系的姿态角均为0°进行计算；当沿轨道负切向点火工作时，将起到减速的作用，减小轨道半长轴，此时上面级本体系轴与轨道系轴反向，相对轨道系的姿态角为俯仰角为180°，其它姿态角均可以为0°。

可以通过沿轨道法向点火工作，进行轨道倾角的控制。当上面级处于升交点（由赤道南向赤道北极飞越赤道）附近时，沿轨道正法向点火工作，可以增大轨道倾角，此时相对轨道系的偏航角为-90°，其它姿态角为0°；沿轨道负法向点火工作，可以减小轨道倾角，此时相对轨道系的偏航角为90°，其它姿态角为0°。当上面级处于降交点（由赤道北向南飞越赤道）附近时，沿轨道正法向点火工作可以减小轨道倾角；相反，沿轨道负法向点火工作可以增大轨道倾角。

可以通过沿轨道径向点火工作，进行轨道偏心率的控制。一般对于近圆轨道，当上面级沿轨道径向点火工作时，可以增大轨道偏心率，但变轨后的近地点所在位置不同。对于椭圆轨道，在由近地点飞往远地点的弧段（升弧段），沿轨道正径向点火工作，可以增大轨道偏心率，此时相对轨道系的姿态角为俯仰角等于90°，其它姿态角为0°；沿轨道负径向点火工作，可以减小轨道偏心率，此时相对轨道系的姿态角为俯仰角等于-90°，其它姿态角为0°。在由远地点飞往近地点的弧段（降弧段），沿轨道正径向点火工作，可以减小轨道偏心率；沿轨道负径向点火工作，可以增大轨道偏心率。

综上所述，上面级机动过程中相对轨道系的姿态角可以确定，利用上述章节中程序角的计算方法便可以求解出上面级的飞行程序角，完成程序角的设计。但需要指出的是，从燃料消耗来说，对于圆轨道机动位置的选择对于轨道参数改变量影响不大；但对于椭圆轨道机动位置的选择对燃料优化较为重要，可以参考霍曼变轨进行设计。

4 算例仿真

拟定用于轨道计算相关的火箭上面级总体参数，采用数值仿真的方法对上述上面级机动程序角设计方法进行验证。仿真采用的火箭上面级总体参数见表1。

表1 火箭上面级总体参数

仿真开始时火箭上面级初始轨道参数见表2。

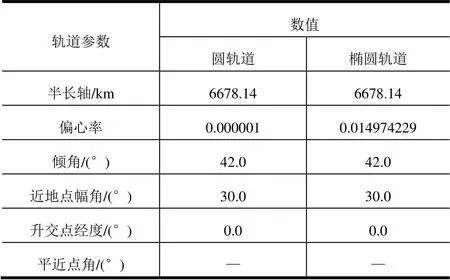
表2 火箭上面级初始轨道参数

对于圆轨道，分别施加切向、法向、径向机动，机动结束后的轨道参数分别见表3~5。从表3可以看出，正切向轨道机动可以增大轨道半长轴，负切向轨道机动可以减小轨道半长轴；从表4可以看出，正法向轨道机动使得轨道倾角增大，负法向轨道机动使得轨道倾角减小，不会引起轨道形状的改变；从表5可以看出，径向轨道机动使得轨道的偏心率增大，不同方向的径向机动可以导致近地点出现的位置不同。

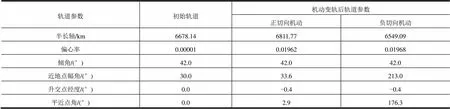
表3 圆轨道施加切向机动变轨参数

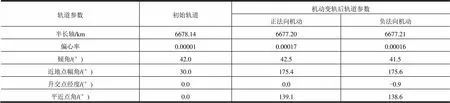
表4 圆轨道施加法向机动变轨参数

注：在轨道升交点附近实施轨道机动

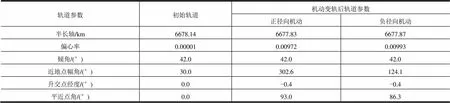
表5 圆轨道施加径向机动变轨参数

对于椭圆轨道，分别施加切向、法向、径向机动，机动结束后的轨道参数分别见表6~8。

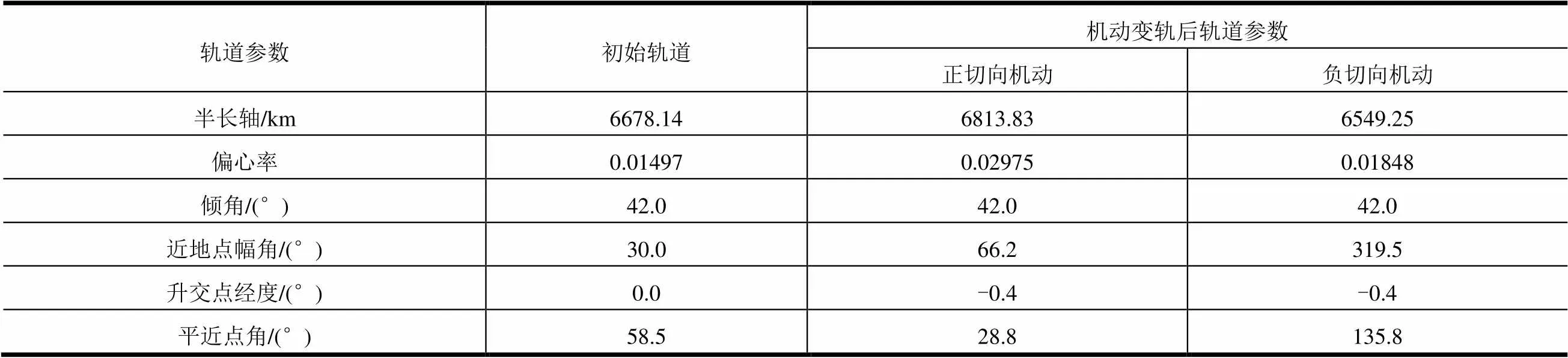
表6 椭圆轨道施加切向机动变轨参数

注：在轨道近地点附近实施轨道机动

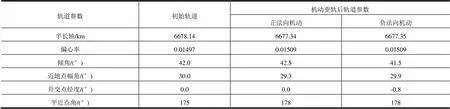
表7 椭圆轨道施加法向机动变轨参数

注：在轨道升交点附近实施轨道机动

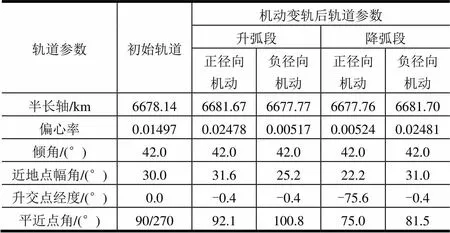
表8 椭圆轨道施加径向机动变轨参数

注：分别在轨道升交点和降交点附近实施轨道机动

从表6可以看出，正切向轨道机动可以增大轨道半长轴，负切向轨道机动可以减小轨道半长轴；从表7可以看出，正法向轨道机动使得轨道倾角增大，负法向轨道机动使得轨道倾角减小，不改变其它轨道参数；从表8可以看出，在椭圆轨道的升弧段进行正径向轨道机动可以增大轨道偏心率，进行负径向轨道机动可以减小轨道偏心率，降弧段的径向机动效果相反。

5 结束语

数值仿真结果验证了上面级机动效果，说明上面级机动程序角设计方法的正确性。从火箭上面级机动段程序角设计出发，基于轨道机动效果所决定的相对轨道系姿态角进行研究，利用转动矩阵计算相对发射惯性系的程序角，完成了机动段飞行程序角的设计，这不同于以往火箭飞行程序角的设计方法，能够提高上面级轨道设计效率。

[1] 余梦伦. 地球同步卫星发射轨道的设计[J]. 中国空间科学技术, 1983, 3 (2): 1~8

[2] 张旭辉, 等. QJ1028B-2008航天产品常用坐标系[S]. 北京: 国防科学技术工业委员会, 2008.

[3] 贾沛然. 远程火箭弹道学[M]. 长沙: 国防科技大学出版社, 2009.

[4] 肖业伦. 航天器飞行动力学原理[M]. 北京: 宇航出版社, 1994.

[5] 吴鹤鸣, 等. 航天动力学基础[M]. 北京: 北京航空航天大学出版社, 1990.

[6] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998.

[7] Mukhopadhyay A K. Application of the graphic flight path design program(FPDP) for fast interactive trajectory design[R]. AIAA-73-113, 1973.

[8] 茹家欣. 空中发射运载火箭发射轨道设计[J]. 现代防御技术, 2004(2): 28-29.

Turning Matrix Method Based Orbit Maneuver Flight Program Angle Design of the Rocket Upper Stage

Wang Chuan-kui, Zhou Wen-yong, Chen Yi, Zhang Li-bin, Xie Yong-feng

（Beijing Institute of Aerospace Systems Engineering, Beijing, 100076）

A program angle design method for orbit maneuver flight of rocket upper stage is presents in this paper. Transform relation of multi-reference frame is adopted to calculate the turning matrix and finally the flight program angle of the upper stage is get. The result of Numerical simulation shows that this method can be used in the design of flight program angle of the upper stage. In order to satisfy different payload orbit parameters, the upper stage that is the bridge between the rocket and satellites can use this method to design orbit.

Turning matrix; Orbit maneuver; Flight program angle

1004-7182(2016)02-0008-05

10.7654/j.issn.1004-7182.20160202

TJ013

A

2014-11-18；

2014-12-01

王传魁（1985-），男，工程师，主要研究方向为航天器/弹轨道设计及优化