基于分解进化算法的飞行器投弹规划*

2018-08-27杨任农

弹箭与制导学报 2018年4期

钟鸣,杨任农,吴军,张欢,张强

(空军工程大学航空航天工程学院,西安 710038)

0 引言

在战争中,夺取制空权的最终目的是利用己方的空中优势来对敌方目标进行打击与压制。在先进无源电子对抗措施的掩护下使用轰炸机携带炸弹进行对地攻击时飞行员往往要承受巨大的过载,难以自己做出最佳的投弹[1]。在解决对地攻击的命中率问题上主要使用精确制导炸弹,但成本过高[2],且易受干扰影响精度[3]。常规航空炸弹因成本低廉、抗干扰,不仅被广泛应用于线状和面状的攻击中[4],也被应用于精确打击中。这对投弹的精度以及空中弹道的要求越来越高[5]。在不同的投弹高度、速度以及姿态俯仰角等投弹条件下,投弹的精度与效果差距较大[6-7]。

在轰炸任务中,可将投弹的规划问题看作一个多目标优化问题,并可根据投弹高度、弹着角度、速度等任务特殊要求做出相应的约束,建立优化模型。运用文献[8]提出的分解的多目标进化算法(MOEA/D)进行求解,仿真结果表明,模型在不同的任务要求下均能作出最优的投弹规划。

1 问题建模

1.1 轰炸过程分析

1.1.1 轰炸流程

在飞行器进行轰炸过程中一般可划分为四个阶段,如图1所示。

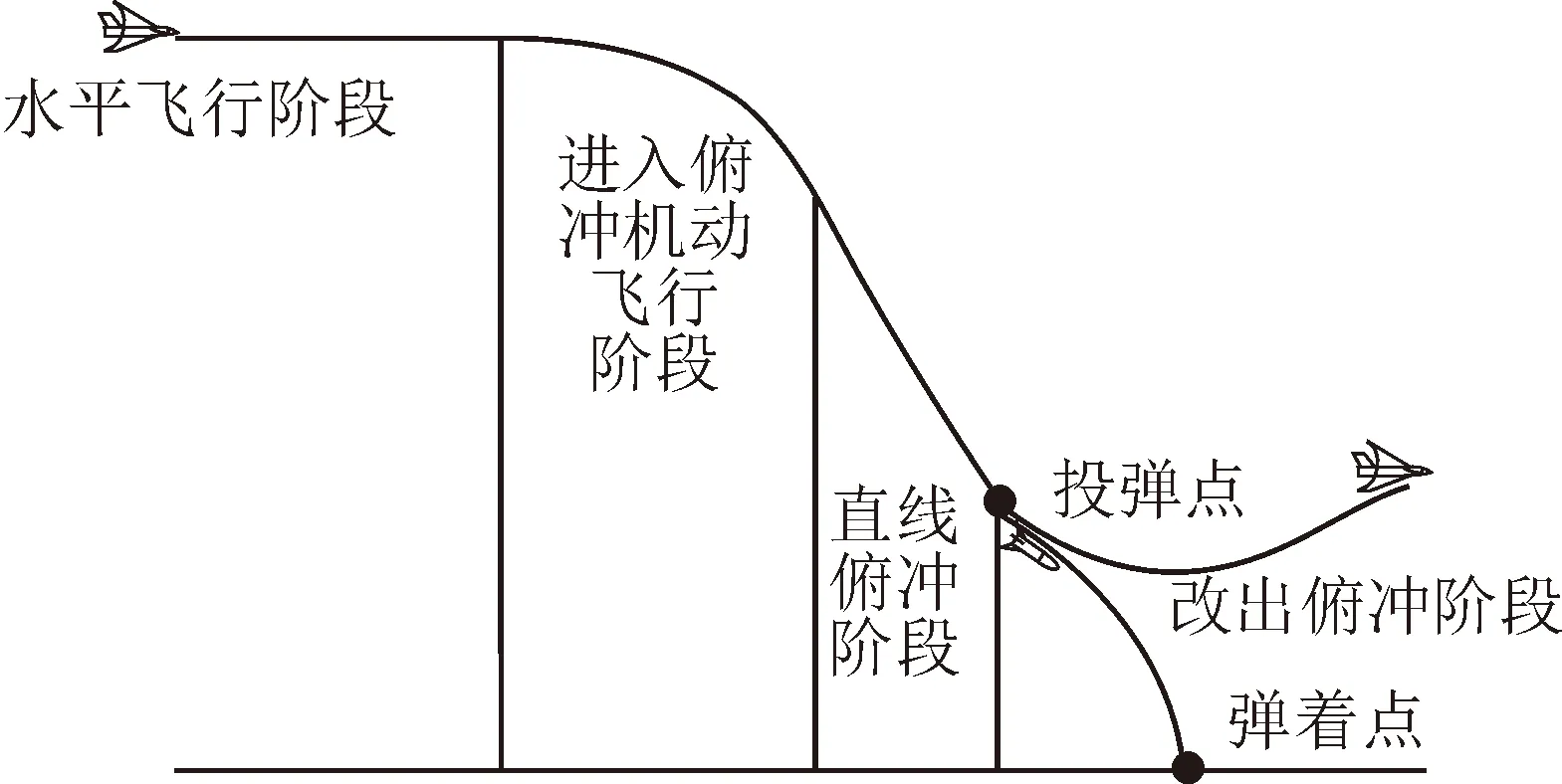
图1 轰炸流程图

1)水平飞行阶段中,飞行器进入轰炸机动的起始点,准备进行机动。2)俯冲机动阶段,在此阶段中飞行器进行机动调整好投弹的角度。3)直线俯冲阶段,在此阶段前投弹的角度已经基本确定,飞行人员需操作飞行器对准目标,并调整好投弹速度,选择投弹时机。4)改出俯冲阶段,在此阶段飞行器已完成投弹动作,在确认战果后应尽快脱离战场,以免遭受防空火力的打击。

1.1.2 投弹原理

影响一次轰炸任务效果的因素主要有3个方面:炸弹攻击威力、攻击精度、飞行器安全性。炸弹在投放后,其飞行轨迹如图2所示。

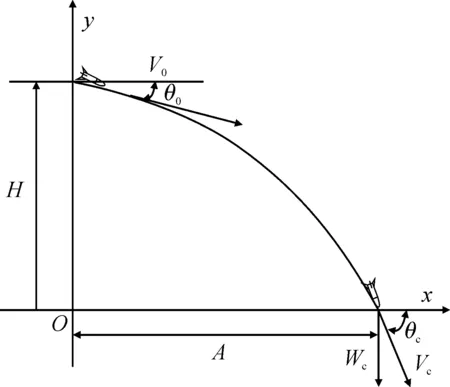
图2 炸弹飞行轨迹图

投弹点的高度为H,炸弹的初始速度为V0,投弹的初始角度为θ0,炸弹水平飞行距离为A。炸弹命中目标时,速度为Vc,炸弹弹轴与水平面的夹角为θc,Wc为速度Vc的垂直分量。在炸弹攻击威力方面,当使用同种型号的炸弹时,增大Wc可以使炸弹获得更大的动量,从而增加穿透力,增大θc可以降低发生跳弹的概率,并增加穿透力。在攻击精度方面,炸弹飞行距离越长,则由于空气阻力等环境因素产生的误差越大,故应尽量缩小炸弹水平飞行距离A。在飞行器安全性方面,飞行高度H越高,则飞行器被防空火力击中的可能性越小。

1.1.3 炸弹飞行轨迹分析

不考虑空气对地面的相对作用[4]。炸弹在投弹点投放后飞行时间t与投弹高度H、炸弹初始速度V0、投弹角度θ相关:

根据求根公式可得时间t:

由飞行时间t、初始速度V0、投弹角度θ可得炸弹水平飞行距离A:

A=V0cosθ·t

也可求得垂直速度Wc:

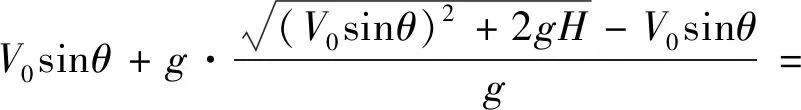
由于忽略空气对炸弹的作用,则炸弹飞行时的水平速度不变,根据弹着垂直分量速度Wc可得弹着角度θc:

1.2 投弹约束分析

在轰炸任务中时常会因任务需求而对轰炸的投弹高度H、弹着角度θc、弹着垂直速度Wc有特殊的要求。因而可将任务分为两类:一类是无特殊要求,仅考虑飞行器性能和环境因素的一般投弹情况,一类是有特殊投弹要求的投弹情况。针对第二种情况,需在第一种情况约束的基础上加入新的约束。

1.2.1 一般投弹约束分析

根据飞行器的性能,对飞行高度H、投弹角度θ、投弹速度V0做出如下约束:

飞行器在投弹后,还需安全的脱离轰炸区域。如图3所示。

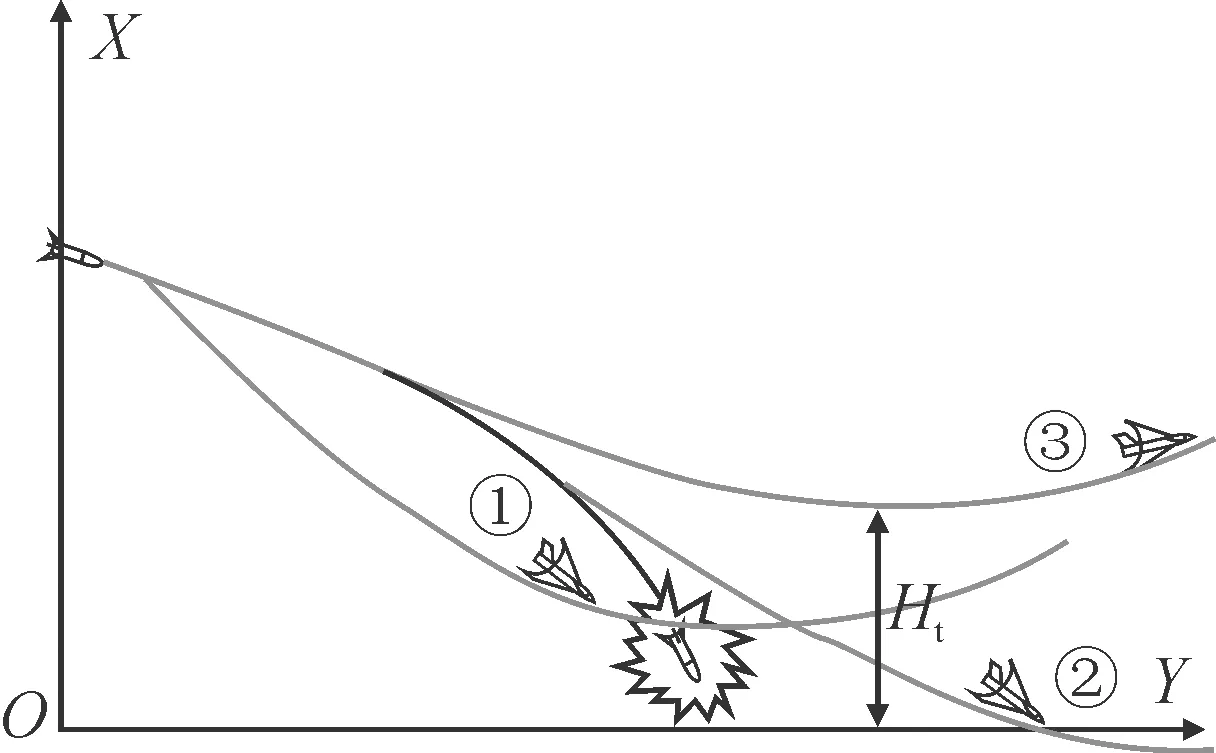
图3 飞行器脱离轨迹图

飞行器在投弹后,若投弹速度过快,投弹高度过低,则如航线①所示,炸弹爆炸时飞行器还未到安全区域,被误伤。若投弹角度过大,投弹高度过低,则如航线②所示,飞行器未能及时拉起,坠地。期望的飞行航线如③所示,飞行器能及时离开爆炸杀伤区域,且能及时拉起距地面的安全高度。如图4所示。

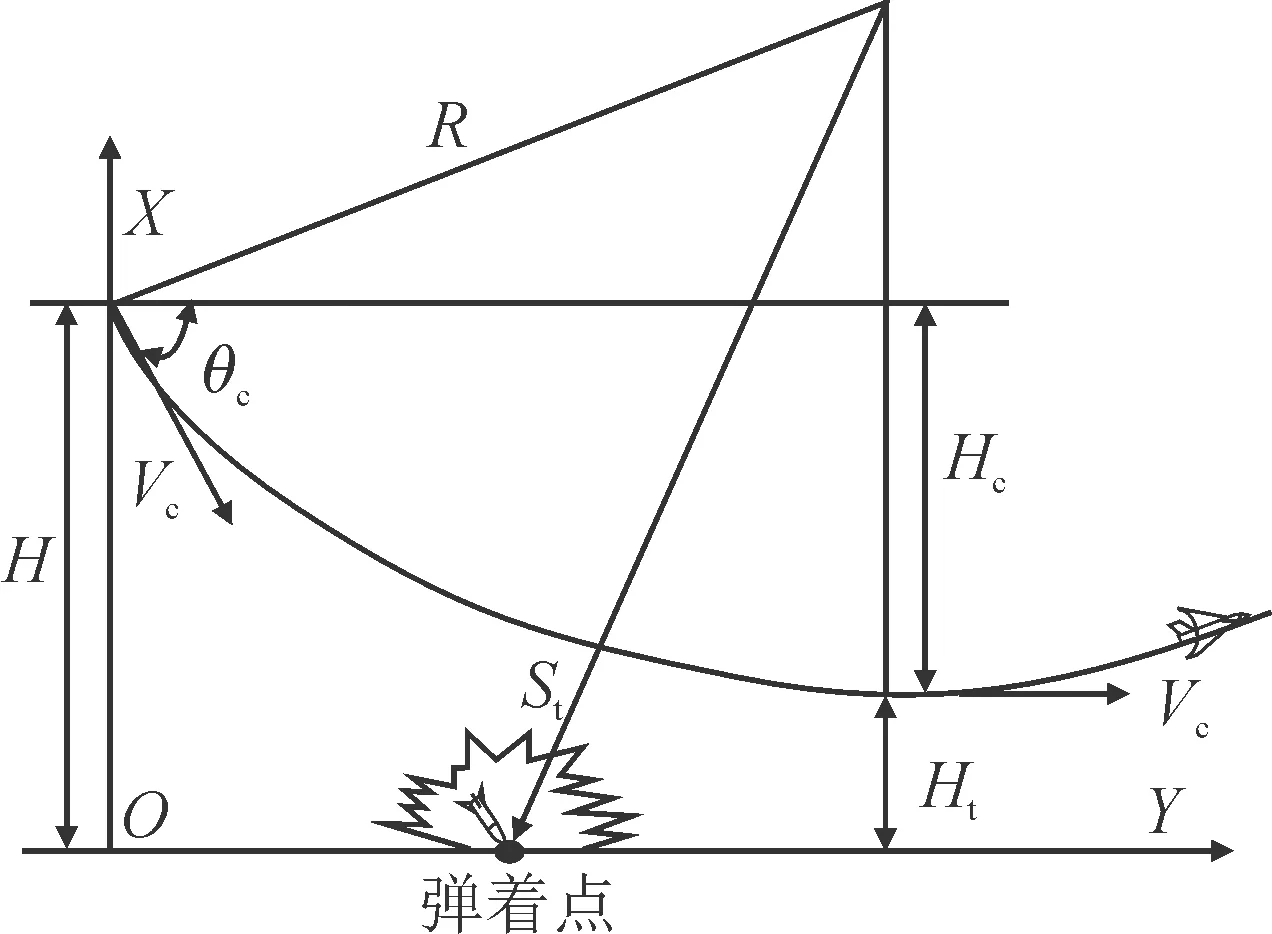
图4 飞行器拉起轨迹分析图

在飞行器投弹后,飞行器脱离轰炸区域的轨迹满足:

式中：Ht为航迹最低点距地面的距离Ht=H-Hc；h为距地面的最低安全距离；Hc为飞行器从俯冲状态到拉起到水平状态所损失的高度；St为航迹距离爆炸点最近距离；r为炸弹爆炸的最大影响半径。飞行器拉起过程即是一个将飞行器从俯冲状态转化为水平飞行状态,即将俯仰角θc转为0°。可将航迹近似的看成一条圆弧,R为航迹的曲率半径,ωc为爬升角速度。

则损失高度Hc:

若将航迹看做一条圆弧,则距爆炸点最近的距离即为圆弧原点到弹着点的长度与圆弧半径的差。即:

1.2.2 特殊投弹要求约束分析

若对投弹高度H、弹着角度θc、弹着垂直速度Wc有特殊要求(W1≤Wc≤W2;θ1≤θc≤θ2;H1≤H≤H2),则可根据1.1节轰炸过程分析对投弹决策变量(H、θ、V0)做出约束:

1.3 优化模型建立

根据以上分析,在没有特殊投弹要求的情况下,仅需考虑飞行器性能和环境对轰炸规划的约束。为取得较好的轰炸效果,对于弹着垂直速度Wc、弹着角度θc、投弹高度H要求越大越好,而对于炸弹飞行时间t则要求越小越好。根据1.1.3节炸弹飞行轨迹分析,可建立飞行器投弹状态优化模型:

若对投弹高度H、弹着角度θc、弹着垂直速度Wc有特殊要求,则将因任务要求而产生的对应约束添加到优化模型中。

2 MOEA/D进化算法应用

2.1 算法概述

MOEA/D进化算法相较于其他的进化算法,其策略是将一个多目标优化问题分解为多个单目标优化问题,然后再对这些单目标问题进行求解[9]。MOEA/D算法在2009年多目标进化竞赛(CEC 2009)上在解决无约束多目标优化问题夺冠[10],MOEA/D进化算法在解决投弹姿态规划此种较为复杂的多目标优化问题具有如下优势:1)目标子问题可通过临近子问题的优化信息来进行优化。与MOGLS和NSGA-II等进化算法相比,其子问题间可协同进化,无需重复优化子问题,提高计算效率[11-12]。2)其擅长处理多个目标子问题的优化问题,在目标问题增多的情况下相对其他算法,其求解性能并没有明显的下降[13]。3)MOEA/D能很好地求解具有复杂多目标优化问题,而这正是在实际工程优化中常遇到的问题[14]。

2.2 染色体编码

模型中的决策变量为投弹高度H、炸弹初始速度V0、投弹角度θ,根据1.3节模型中决策变量的取值范围运用随机的方法产生n×m的矩阵,其中n为决策变量的个数,即染色体长度,m为种群的规模。每条染色体即为一条轰炸规划航线。

2.3 算法流程

算法流程如图5所示。

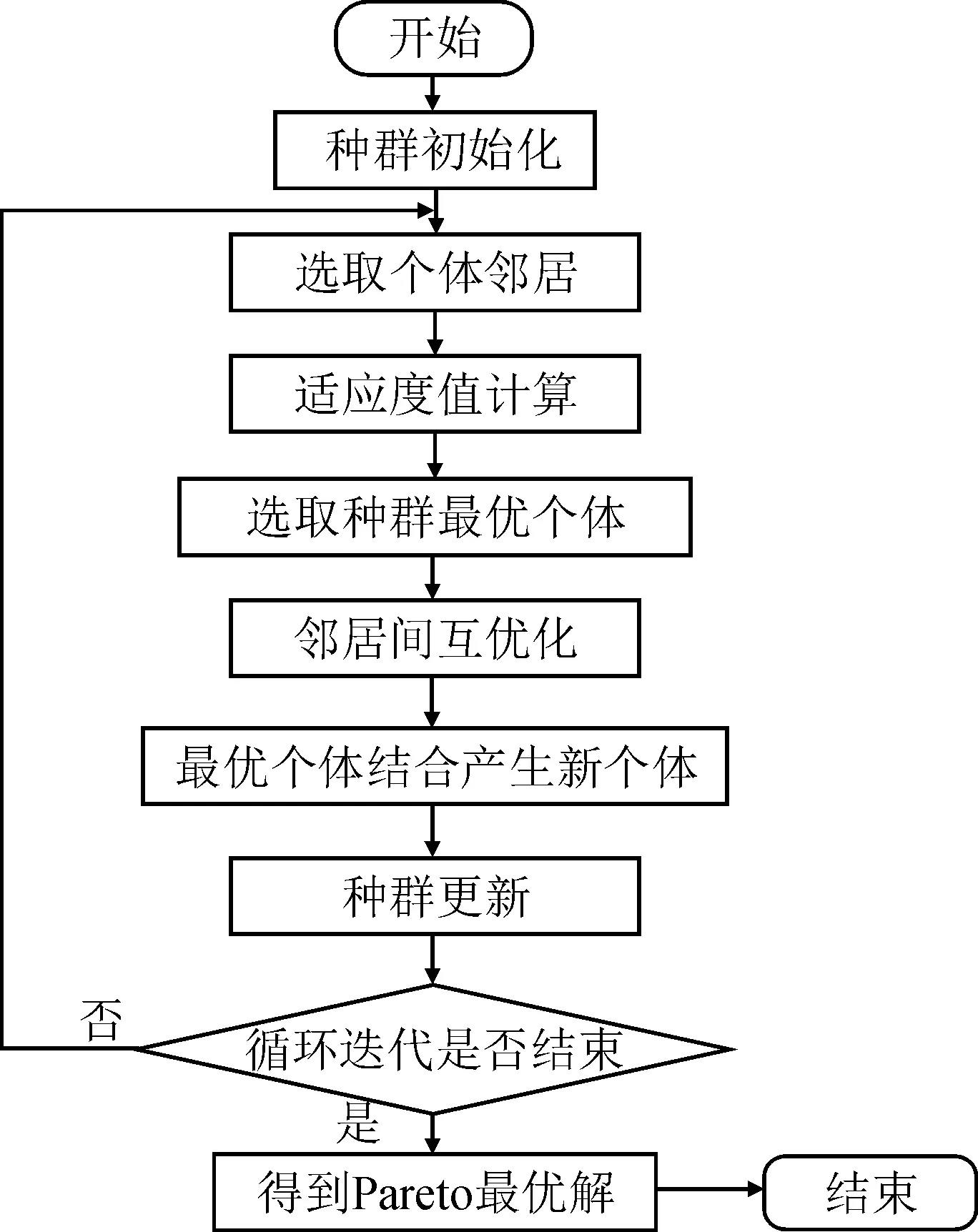
图5 算法流程图

3 仿真结果与分析

在MATLAB 2014a环境下对投弹进行仿真。针对无特殊投弹要求,有投弹高度要求,有弹着角度要求这3种情况进行仿真。

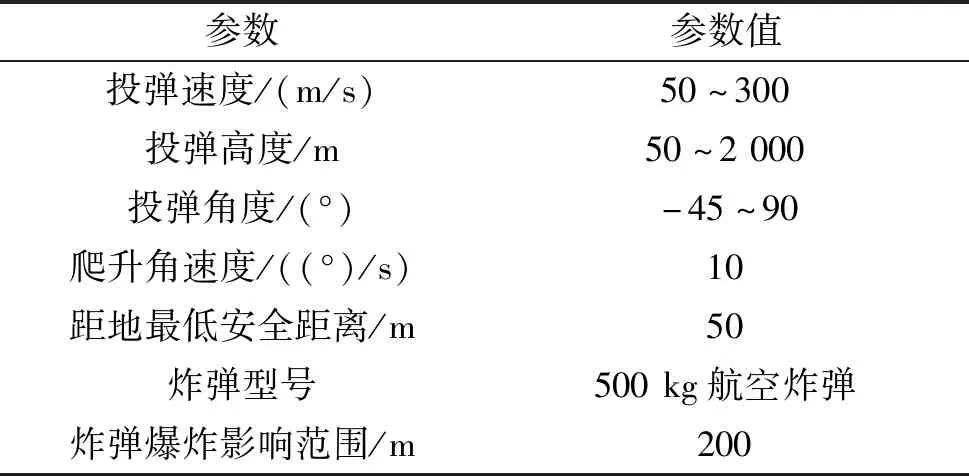
表1 飞行器投弹参数

表2 投弹任务要求

表3 算法参数设置

仿真结束后,任务一,任务二,任务三规划的Pareto前端图如图6所示。

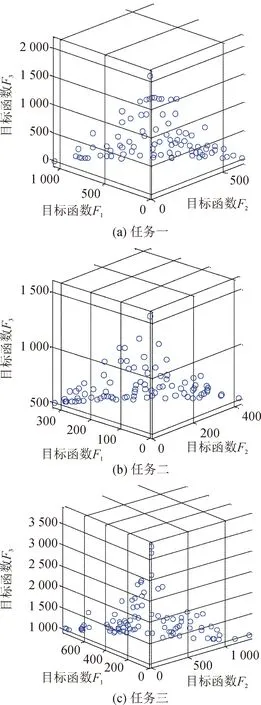
图6 Pareto前端图

在任务一的规划中,飞行器在1 800 m高度投弹,投弹速度为180～220 m/s,投弹角度为15°～25°时轰炸效果最好。在任务二中,投弹飞行器投弹高度在500～1 500 m时,投弹速度在160～200 m/s,投弹角度在20°～30°之间效果最好。在任务三中,要求弹着角度为45°～60°,则投弹高度应在2 000～2 500 m,投弹速度在160～200 m/s,投弹角度15°～25°。

将规划的投弹参数代入到模型中进行检验,经检验投弹参数满足模型中各约束的限制,并能够完成投弹任务的要求。