基于功能截面分解的大型横梁拓扑优化

吴凤和　史红亮　许晓鹏　范俊伟

燕山大学，秦皇岛，066004



吴凤和史红亮许晓鹏范俊伟

燕山大学，秦皇岛，066004

摘要：针对复杂载荷工况下横梁等大型三维结构件拓扑优化结果可读性差、无法对结构优化提供有效指导的问题，提出基于功能截面分解的拓扑优化方法。基于力的分解与等效原理，将三维实体分解为三个平面内的二维功能截面，根据各功能截面的受力方式确定其抗弯或抗扭属性；在此基础上，分别对两个主要承载的功能截面进行二维拓扑优化分析，并综合二维功能截面分析结果完成三维实体的整体拓扑优化，实现了将三维实体拓扑优化问题转化为二维功能截面的拓扑优化问题。以CXK5463车铣加工中心横梁为例，对结构拓扑优化效果进行了验证，仿真实验结果表明，功能截面分解方法可以得到清晰的应力传递路径，在保证横梁静动态特性基本稳定的基础上，横梁减重12.67%，优化效果较为明显。提出的方法可为大型、重型复杂结构件的拓扑优化研究提供借鉴与参考。

关键词：拓扑优化；横梁；功能截面；有限元分析

0引言

横梁是车铣加工中心等大型机床的重要部件，其上通常安装主轴等关键功能部件，因此，其静动态性能将直接影响机床精度。为提高横梁的静动态性能，可采用拓扑优化及尺寸优化等方法对其进行结构优化。近年来，国内外在结构优化方面取得了一系列成果。张氢等[1]提出了一种“整体层-局部层”的两层优化模型，并对浮吊金属结构的整体进行了结构优化；王欣等[2]采用材料变密度的方法对起重机臂截面结构进行了拓扑优化设计；饶柳生等[3]基于相对密度法对机床立柱的筋板进行了优化设计；隋允康等[4-7]提出ICM(独立、连续、映射)方法，并基于此方法成功地对多工况下刚架及三维连续体进行了结构拓扑优化；满佳等[8]提出了一种基于元结构的数控机床结构优化设计方法，并以内齿轮铣齿机床的立柱为例进行了优化设计；文献[9-11]采用尺寸优化的方法对结构件进行优化设计。由于机床横梁的内部壁板等呈复杂三维结构，且横梁在工作时承受的是复杂空间载荷，故而采用上述传统拓扑优化方法进行横梁结构优化设计很难得到满意的结果。

针对大型结构件的拓扑优化问题，王晓煜等[12]提出了一种结构拓扑优化新方法，根据受力情况将龙门加工中心横梁部件分解为纵、横截面，对两个截面的筋肋分布形式分别进行拓扑优化，根据截面拓扑优化模型建立了横梁的三维优化模型，但该方法仅优化了竖直截面上的筋肋布置形式，未将其他两个截面的拓扑优化融入到优化模型中，优化结果不够充分；Querin等[13]、荣见华等[14]发展了双方向渐进结构优化法，通过应力灵敏度来考虑全局应力的影响，减缓了ESO法基于局部应力的限制，提高了探索全局优化解的能力，然而在实施过程中会出现少量孤立体的奇异结构，使得结构拓扑优化无法进行，因此，该方法仅适合一些简单三维结构的拓扑优化设计；Chen等[15]将遗传算法应用到连续体结构的拓扑优化中，为解决二维和三维连续体结构拓扑优化问题提供了较好的方法，但该算法需要大量的计算时间；荣见华等[16-19]对不同应力准则下连续体结构的拓扑优化方法进行了研究，并提出了一种基于人工材料的双向渐进结构优化方法用来改善优化过程中的数值计算问题，将相应的渐进结构优化方法进一步推广到了三维结构优化中；孔文秦[20]针对应力约束问题，提出了在优化迭代中允许大量添加单元的算法，增强了寻找优化传力路径、获得优化拓扑和形状的能力，避免了优化过早地收敛到局部最优解。上述研究虽然在多载荷工况下的三维机械结构的拓扑优化方面取得了一定的进展，但却存在常常得到局部最优解而非全局最优解的缺点，使拓扑优化概念模型可读性差，无法为结构优化设计提供有效指导。另外，现有研究大多局限于单一载荷工况下的拓扑优化或二维结构拓扑优化，而针对复杂载荷工况下的三维结构拓扑优化问题则研究得很少。

在上述背景下，本文以CXK5463型车铣加工中心的横梁为研究对象，开展复杂载荷工况下大型结构件三维拓扑优化研究，根据力的分解及等效原理，提出基于功能截面分解的拓扑优化方法。

1复杂载荷工况下大型结构件拓扑优化存在的问题

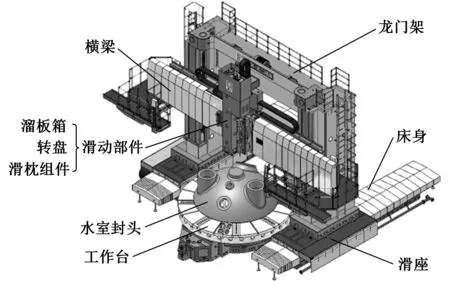
图1　CXK5463龙门移动式车铣加工中心外观图

图2　横梁结构模型图

图3　横梁内部结构爆炸示意图

本文以CXK5463车铣加工中心横梁为例对复杂载荷工况下大型结构件拓扑优化问题进行说明。CXK5463车铣加工中心为重型金属切削数控机床，主要用于核电关键零件水室封头的特殊内外形的精确加工。如图1所示，该机床采用动梁龙门移动布局，由左右床身、左右滑座、左右立柱、连接梁、横梁、旋转工作台、溜板箱、转盘、铣削主轴箱、滑枕等部件组成。横梁部件(图2)可在龙门架上沿导轨面实现垂直方向移动，主要由横梁、滑鞍、滑动组件等组成。横梁长度10.4 m，跨距7.5 m，宽1.28 m，高1.8 m，根据横梁受力情况和传统结构设计方法，内部设置以井字形为主的加强筋板，内部筋板设置情况如图3所示。如图4所示，机床横梁部件受力结构为两点简支梁支承，横梁部件在工作时所承受的复杂空间载荷包括加工时产生的切削力、自身重力、移动部件和固定部件相对运动时导轨面间的摩擦力、连接大件和移动部件间的连接力、惯性力、冲击或振动干扰力以及温度升高时产生的热应力。除了横梁结构本身自重造成稳定变形以外，当横梁上的滑动部件从一端移动到其他位置时，也会引起横梁不稳定的弯曲变形。此外，由于结构的原因，滑枕及主轴箱呈悬臂结构，其重力形成的弯矩也使横梁产生扭转变形，引起主轴箱前倾。横梁在垂直方向上的刚度对机床总刚度影响很大。刚度小的横梁其变形量有时可占到机床综合变形量的20%～40%，其中，又以扭转变形为主，约占60%。

图4　横梁约束与载荷设置示意图

考虑到拓扑优化过程中应设置为机床常态下的负载条件，因此设置横梁受到自身重力作用，移动部件的重力以远端力的形式施加在横梁与滑动部件接触的导轨上表面，加载位置为移动部件的质心坐标处；将横梁与立柱的两个结合面设置为固定边界条件。载荷施加情况如图4所示。

根据退化原理，横梁结构需要事先“填充”成实心作为退化计算的设计空间，如图5所示。为了得到拓扑优化的合理筋板参数，横梁实心模型的网格尺寸应尽可能地精细。经过多次试算，单元数量控制在40万个以内，在设定目标质量为横梁原型的60%时得到图6所示的建议保留的结构。

图5　横梁实心体优化空间模型

图6　横梁三维实心模型的拓扑优化结果

从横梁三维实心体拓扑优化结果来看，拓扑建议的横梁内部结构过于单一，材料聚集严重，可读性差，不能为横梁内部筋板的合理设计提供指导。这也体现了复杂应力工况下大型结构件三维拓扑优化常常得到局部最优解而非全局最优解的问题。因此，有必要寻求拓扑优化新途径，得到清晰的应力传递路径，为大型结构件整体形貌和筋肋合理布置提供有效指导。

2功能截面分解法

2.1功能截面分解法原理

根据理论力学相关原理，承受复杂载荷物体的受力情况可简化为图7所示的情况，通过选取物体上的一点(例如结构件的质心，图7为第一象限图)作为原点建立直角坐标系Oxyz，将空间力系简化到这一点，就可以将主矢与主矩分解到坐标系的三个坐标轴上。

图7　功能截面分解法示意图

以图7所示的受力情况为例，本文将XY平面、XZ平面、YZ平面定义为二维功能截面，其中XY平面为分力Fz的抗弯功能截面以及分力矩Moz的抗扭功能截面；XZ平面为分力Fy的抗弯功能截面以及分力矩Moy的抗扭功能截面；YZ平面为分力Fx的抗弯功能截面以及分力矩Mox的抗扭功能截面，如表1所示。取Fx、Fy、Fz中最大分力所对应的平面为主要抗弯功能截面；取Mox、Moy、Moz中最大分力矩所对应的平面为主要抗扭功能截面。主要抗弯功能截面和主要抗扭功能截面作为两个主要功能截面，第三个平面作为次要功能截面；当主要抗弯功能截面与主要抗扭功能截面为同一个截面时，此截面作为主要功能截面，而第二个主要功能截面根据分力影响较大还是分力矩影响较大，来选取第二大的分力或分力矩所对应的平面，最后一个平面作为次要功能截面。

表1　功能截面与分力及分力矩关系

2.2基于功能截面分解的拓扑优化步骤

基于功能截面分解的拓扑优化步骤如下：①假设物体分别受力F及力矩M(图7中未标出)作用，受力分析结果如图7所示；②假设Fx≥Fy≥Fz且Moz≥Moy≥Mox，则YZ截面为主要抗弯功能截面，XY截面为主要抗扭功能截面，XZ截面为次要功能截面；③分别对YZ截面和XY截面进行截面拓扑优化；④根据XY、YZ两个主要二维功能截面的拓扑优化结果，综合建立三维初始原型，再针对先前未考虑的XZ次要功能截面进行整体三维拓扑优化，最终完成大型机械结构件的三维拓扑优化并校验优化效果。

应用该方法可解决复杂载荷工况下零部件三维结构拓扑优化模型可读性差的问题，在结构设计初期可提供有效的指导。

3基于二维功能截面分解的横梁拓扑优化过程

3.1基于功能截面分解的机床横梁拓扑优化步骤

本文以机床横梁为例开展基于功能截面分解的大型结构件拓扑优化研究，具体步骤如下(图8)：

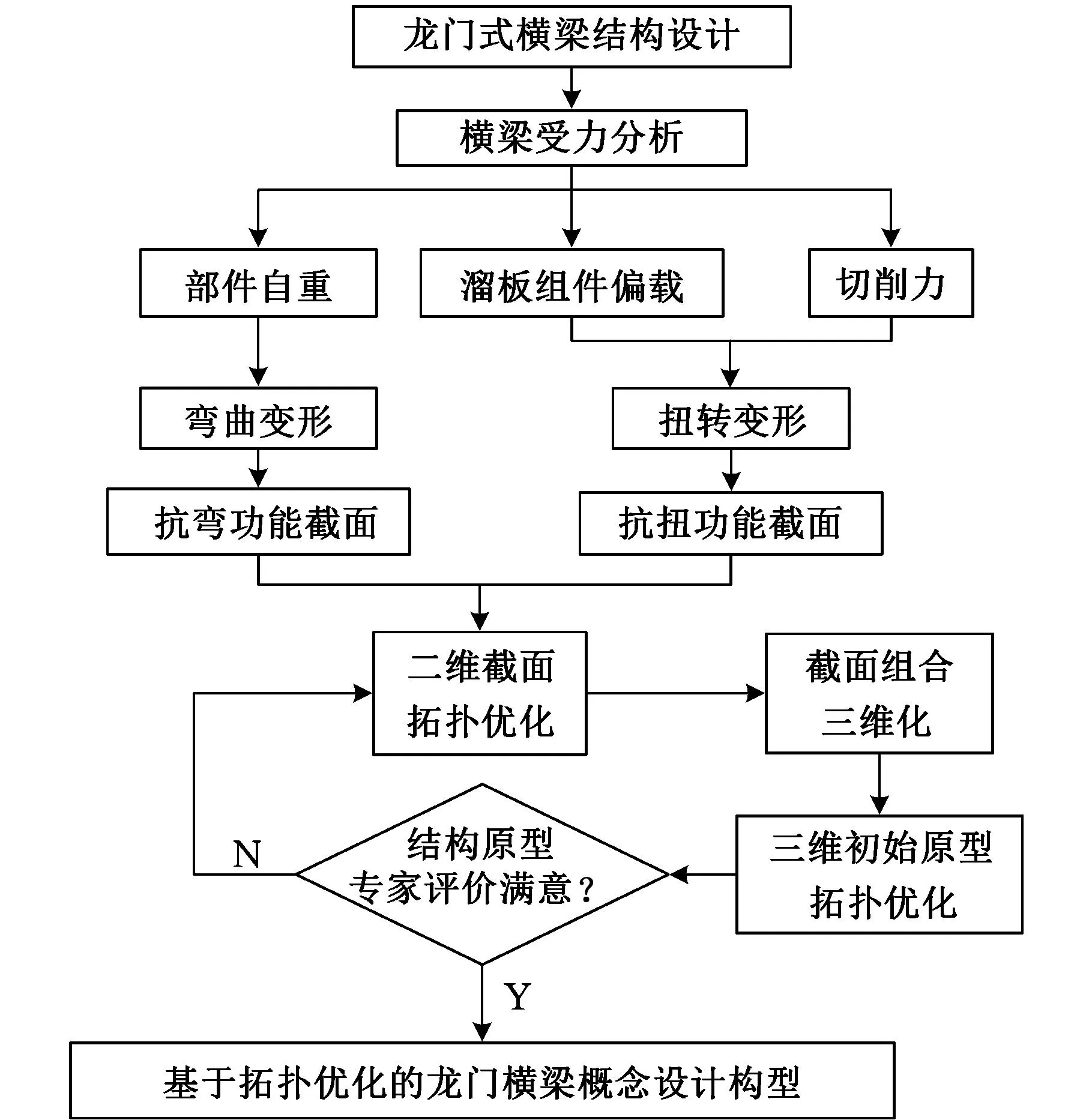
图8　基于功能截面分解的横梁拓扑优化设计技术路线

(1)受力分析。以横梁的质心为原点建立图7所示的坐标系，根据力的平移原理，横梁常态下的多个复杂载荷可以等效为两个负载，即垂直向下的压力和作用在接触面上的转矩。

(2)确定主要、次要功能截面。垂直向下的压力导致横梁的弯曲变形，转矩导致横梁的扭转变形，因此可以认为，在静载荷作用下横梁的主要功能为抵抗整体弯曲变形和扭转变形。从三维空间解耦的角度看，YZ平面上的材料主要承担抵抗整体弯曲变形的功能，XZ平面上的材料主要承担抵抗扭转变形的功能，而XY平面虽然拥有抵抗整体弯曲变形和扭转变形的能力，但不承担主要的等效负载，为次要功能截面，可暂不考虑。

(3)对主要功能截面进行拓扑优化。因为简单应力下二维平面拓扑优化可以得到清晰的符合工程实际的拓扑概念模型，所以可以近似地将YZ平面(抗弯功能截面)与垂直向下的负载相对应，进行抗弯功能截面上的二维拓扑优化；再将XZ平面(抗扭功能截面)与扭矩负载相对应，进行抗扭功能截面上的二维拓扑优化，以寻找最优的截面形状。

(4) 综合主要、次要功能截面的拓扑优化。将抗弯功能截面和抗扭功能截面的拓扑模型综合起来，并针对先前未考虑的XY功能截面，进行整体三维拓扑优化，最终完成横梁三维形貌优化构型。

为了使截面厚度尺寸不影响求解效果，本文对横梁厚度取较小尺寸。经过数次拓扑优化试算，拟定截面设置方案如下：

(1)图9所示为抗弯功能截面，即YZ拓扑截面，其截面尺寸为6850mm×1580mm，截面厚度取10mm。

(2)图10所示为抗扭功能截面，即XZ拓扑截面，其截面形状按原横梁外形建模，截面厚度取10mm，并按立柱导轨面分割为Ⅰ、Ⅱ两个截面。

图9　抗弯功能截面(YZ拓扑截面)

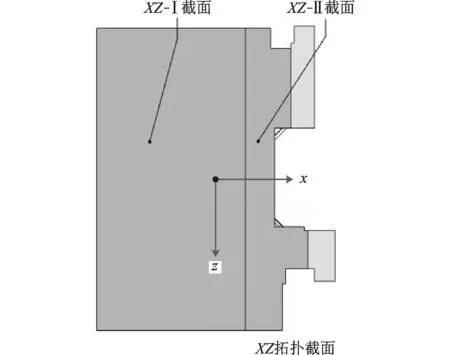
图10　抗扭功能截面(XZ拓扑截面)

3.2二维拓扑概念模型

二维截面的拓扑优化采用实体单元Solid186网格划分，单元尺寸控制在10mm以内。对截面施加相同的约束，并分别施加弯曲载荷(重力)、扭转载荷(远端力)。拓扑优化材料去除率设置为60%～80%，拓扑优化建议保留的结构如图11、图12所示，其中，小圆圈出部分为建议去除的材料。

(a)材料去除率为75%

(b)材料去除率为65%图11　抗弯功能截面(YZ截面)的拓扑优化建议结构

(a)XZ-Ⅰ截面拓扑结果　(b)XZ-Ⅱ截面拓扑结果(c)Ⅰ、Ⅱ截面叠加后的拓扑结果图12　抗扭功能截面(XZ截面)的拓扑优化建议结构(隐去上下导轨)

3.3横梁三维概念设计模型的建立

对二维功能截面拓扑优化的结果进行分析和讨论，得到如下结论：

(1)抗弯功能截面拓扑优化结果(图11)显示了横梁YZ截面的建议筋板布置形式。左右支撑部位由X形筋板构成，支撑部位需要加强筋；中部由形状为“八”字形的筋板构成，且在中部的横梁的上下顶板较厚。

(2)抗扭功能截面拓扑优化结果(图12)显示了横梁XZ截面的建议外形形状。横梁后部外形筋板的各边角应倒角化，以利于扭矩在形状方向上的流动，减小应力集中；前部筋板应相应去除边角，以配合截面形状倒角化，根据制造性要求，前部筋板的孔洞暂不设置。

由此可见，横梁功能截面的二维拓扑优化结果较为清晰，为形状优化设计提供了良好的方向指导。按照拓扑优化的结果，建立抗弯功能截面(YZ截面)和抗扭功能截面(XZ截面)的优化构型，如图13、图14所示。

图13　YZ截面内部筋板布置的概念构型

(a)原横梁XZ截面外形

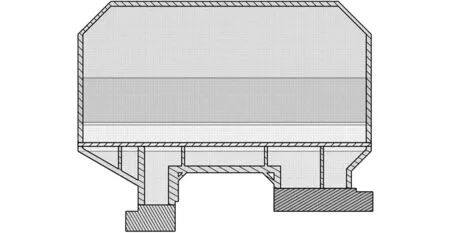
(b)根据拓扑优化修改后XZ截面外形图14　XZ截面外形的形状优化构型

按照二维功能截面拓扑优化得到的截面优化结构，建立基于拓扑优化的横梁优化设计三维初始原型。针对前面2D截面拓扑优化无法解决XY截面材料分布的问题，对初始原型再进行三维拓扑优化，从而有针对性地对初始原型的筋板布置及外形形状作进一步修改。再拓扑优化结果如图15所示。

图15　初始原型的再拓扑优化建议去除结构

对初始原型再拓扑优化结果进行分析，可以看出，初始原型的三维拓扑优化结果具有很强的针对性，可以按照拓扑优化的建议进一步修改初始原型。图15显示,在XY截面上，横梁顶部的筋板的边角部分可以去除(图中方框所示)，根据该建议进一步修改横梁的外形形状，结果如图16所示。

(a)原横梁XY截面外形

(b)根据拓扑优化修改后XY截面外形图16　XY截面外形的形状优化构型

综合上述横梁三个截面上的分析与优化结果，建立横梁的三维形状优化模型如图17所示。

图17　基于拓扑优化的横梁结构形状优化构型(隐去上下导轨)

3.4横梁结构优化及优化效果验证

3.4.1横梁结构的多目标参数优化

根据得到的基于拓扑优化的横梁三维概念设计的结构原型，将结构原型的筋板布局和尺寸参数作为优化变量，按照静态、动态特性分析的方法施加相应的约束和载荷，取质量最小、最大位移最小和一阶固有频率最大为多目标优化问题的三个优化目标，在ANSYSDesignXplorer中进行优化设计。

在Pro/Engineer中建立横梁结构原型的CAD参数化模型，把需要优化的尺寸参数按照AWE与CAD数据传递规则进行重命名，以便在AWE中得到相应的参数变量作为原始设计变量。建立的横梁CAD模型参数示意如图18所示，原始设计如表2所示。其中，Angle1～Angle5为角度参数，L1、L2为宽度参数，T3～T6为厚度参数。

(a)XY、XZ截面上的参数示意

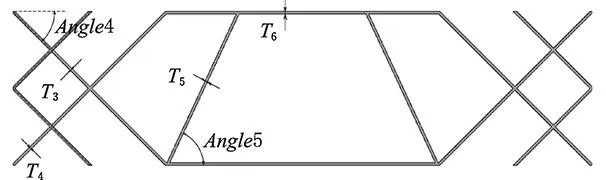
(b)YZ截面上的参数示意图18　横梁结构的参数示意图

位置参数名初值横梁顶盖(XY、XZ截面)Angle1(°)45Angle2(°)45L1(mm)300L2(mm)300Angle3(°)15内部筋板(YZ截面)Angle4(°)40T3(mm)30T4(mm)30Angle5(°)70T5(mm)30T6(mm)30

表3所示为横梁多目标参数优化的原始输出参数。最大位移响应Def_Total表征横梁结构的总体静刚度情况，应越小越好；横梁总体质量Mass一定程度上体现了横梁的制造成本和轻量化目标，应越小越好；提高机床一阶固有频率Freq_1是提高机床刚性、避免共振、降低振幅的有效措施，应越大越好。所以选择Def_Total、Mass和Freq_1三个参数作为多目标参数优化的目标参数。表3中，Def_X 、Def_Z 分别为横梁X、Z方向的静态最大位移响应，Def_Total为横梁静态最大位移响应，Equa_Stress为最大等效应力。

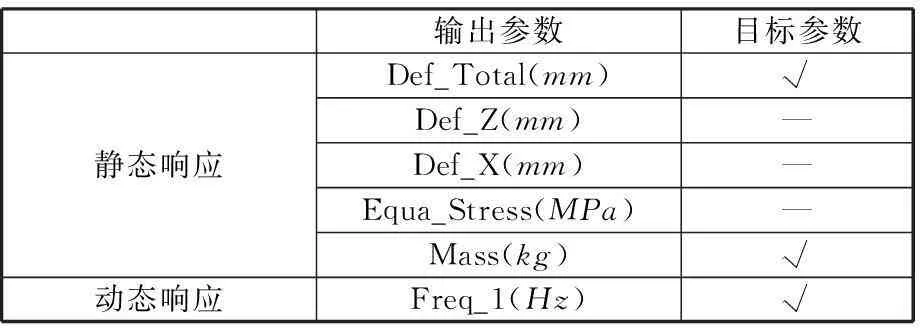
表3　横梁多目标参数优化的原始输出参数

注：“√”表示选择该参数为目标参数；“—”表示不选择该参数为目标参数。

为了有效地进行结构多目标参数优化，本文采用设计参数的灵敏度分析(又称敏度分析)，选择那些对动静态特性影响较大的设计参数作为设计变量，并依据灵敏度值的大小和正负，对设计参数进行修正。将Angle4、T3、T4、T5、T6、Angle5作为设计变量，获得横梁多目标参数优化的最优解。最优解圆整结果如表4所示。

表4　横梁多目标参数优化的最优解

注：“√”表示选择该参数作为相应的变量；“—”表示该参数不予选择。

按照横梁的吊装、装配等实际要求进行小范围局部修补，最终优化后横梁内部结构(隐藏上下导轨)如图19所示。

图19　横梁优化后结构模型(上下导轨隐藏)

3.4.2横梁优化效果验证

为验证优化效果，对拓扑优化前后的横梁部件的静动态特性进行有限元分析。图20所示为静刚度对比结果。

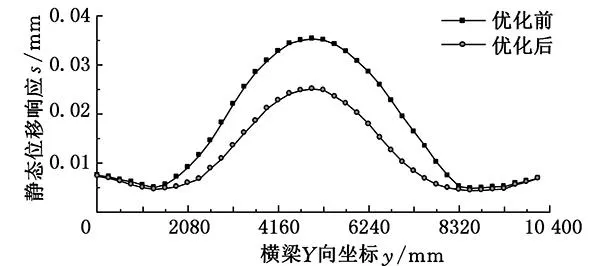
图20　优化前后横梁在Y方向上最大位移响应曲线对比

优化后横梁部件在滑动部件不同Y行程下最大位移响应值如图21如示，其中，DP1～DP11为滑动部件在横梁Y向行程时在横梁Y向上选取的11个关键位置点，P1-Plane4.H5为横梁与溜板箱配合面在横梁上的坐标，P2-DS_journeyY为滑枕组件在横梁上Y向的行程。根据计算的结果绘制优化前后该响应值的曲线如图22所示。

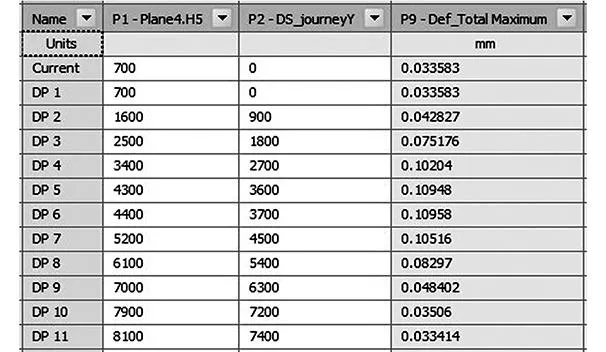
图21　优化后滑动部件在不同Y行程下横梁最大位移响应值

图22　优化前后滑动部件在不同Y行程下横梁最大位移响应曲线对比

由图20和图22所示横梁零件、部件的静态响应曲线可知，优化前后横梁零件、部件的变形量均明显减小，尤其在横梁的中部附近减小明显，表明横梁的静刚度在其中部附近提高明显。取Y向行程3700mm即滑动部件在横梁中央位置时的各静态特性参数结果进行对比，以验证横梁结构优化设计的效果，如表5所示。

表5　横梁结构优化前后的静态特性和质量对比

对优化前后的横梁结构做模态分析比较，横梁结构前6阶固有频率对比如表6所示。从对比数据可知，优化后的横梁结构在静动态特性上均较优化前得到明显提升，横梁静态最大位移响应减小19.82%，最大应力值也远小于许用应力；在动态特性方面，除第6阶固有频率有3.64%的下降以外，前5阶固有频率均有提高，动态性能有所提高。可见，通过对横梁的拓所扑优化和尺寸优化，不仅实现了横梁的轻量化，也提高了横梁的基频。

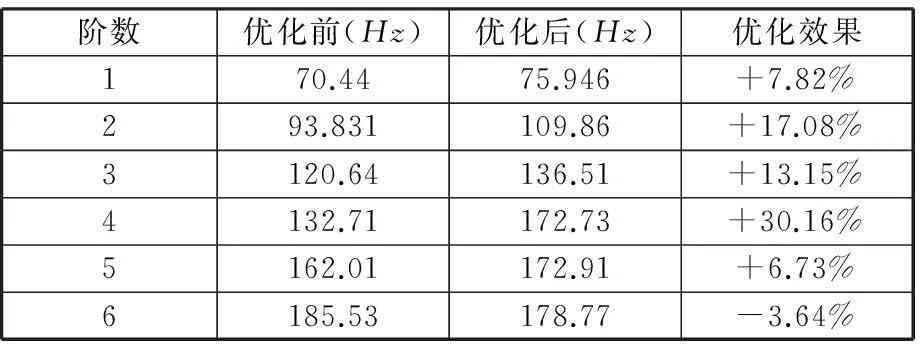
表6　横梁结构优化前后的固有频率对比

4结论

(1)本文采用功能截面分解法研究了处于复杂应力工况下的机械结构件三维拓扑优化问题。功能截面分解法可将复杂载荷等效分解为多个简单载荷并分别与拟定出的横梁二维功能截面进行功能对应，实现将三维拓扑优化问题转化成为二维功能截面的拓扑优化问题，能够得到清晰而又具有指导意义的优化设计概念模型，避免了传统三维实体拓扑优化结果材料聚集严重、可读性差的问题。

(2)利用功能截面分解法对处于重力及弯矩载荷下的算例进行了拓扑优化计算，得到了同时满足静动态性能和轻量化要求的最优结构，验证了本文优化方法对大型、重型复杂机械结构优化设计的实用性。

(3)由于大型结构件工况条件的复杂与多样性，个别构件的工况可能因某种程度的耦合而无法进行功能截面分解，对于此种情况尚需探索其他方法。

参考文献：

[1]张氢,高倩,秦仙蓉,等. 一种由整体到局部的机械结构分层优化模型[J]. 机械科学与技术, 2010, 29(11): 1433-1437.

Zhang Qing, Gao Qian, Qin Xianrong, et al. A Global to Local Hierarchical Optimization Model of Mechanical Structures[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(11): 1433-1437.

[2]王欣,黄琳,高媛,等. 起重机伸缩臂截面拓扑优化[J]. 大连理工大学学报, 2009, 49(3): 374-379.

Wang Xin, Huang Lin, Gao Yuan, et al. Topological Optimization for Crane Telescopic Boom-section[J]. Journal of Dalian University of Technology, 2009, 49(3): 374-379.

[3]饶柳生,侯亮,潘勇军. 基于拓扑优化的机床立柱筋板改进[J]. 机械设计与研究, 2010, 26(1): 87-92.

Rao Liusheng, Hou Liang, Pan Yongjun. Improvement of the Rib Plate in Machine Tools Column Based on Topology Optimization[J]. Machine Design and Research, 2010, 26(1): 87-92.

[4]隋允康,任旭春,龙连春,等. 基于ICM方法的刚架拓扑优化[J]. 计算力学学报, 2003, 20(3): 286-289.

Sui Yunkang, Ren Xuchun, Long Lianchun, et al. Topological Optimization of Frame Based on ICM Method[J]. Chinese Journal of Computational Mechanics, 2003, 20(3): 286-289.

[5]隋允康,叶红玲,杜家政.结构拓扑优化的发展及其模型转化为独立层次的迫切性[J].工程力学, 2005, 22(增): 107-118.

Sui Yunkang, Ye Hongling, Du Jiazheng. Development of Structural Topological Optimization and Imminency of Its Model Transformation into Independent Level[J]. Engineering Mechanics, 2005, 22(S): 107-118.

[6]叶红玲,隋允康. 基于ICM方法三维连续体结构拓扑优化[J]. 固体力学学报, 2006, 27(4): 387-393.

Ye Hongling, Sui Yunkang. ICM-based Topological Optimization of Three-dimensional Continuum Structure[J]. Acta Mechanica Solida Sinica, 2006, 27(4): 387-393.

[7]朱润,隋允康. 基于ICM方法的多工况位移约束下板壳结构拓扑优化设计[J]. 固体力学学报, 2012, 33(1): 81-90.

Zhu Run, Sui Yunkang. Topological Optimization of Plate-and Shell-like Structures with Displacement Constraints under Multi-state Loadings Based on ICM Method[J]. Chinese Journal of Solid Mechanics, 2012, 33(1): 81-90.

[8]满佳,张连洪,陈永亮. 基于元结构的机床结构可适应优化设计方法[J]. 中国机械工程, 2010, 21(1): 51-54.

Man Jia, Zhang Lianhong, Chen Yongliang. An Adaptable Optimization Design Method of Machine Tool Structures Based on Unit Structure[J]. China Mechanical Engineering, 2010, 21(1): 51-54.

[9]汪列隆,朱壮瑞,张建润. 基于APDL的机床大件筋板结构尺寸的优化设计[J]. 轻工机械, 2006, 24(4): 60-62.

Wang Lielong, Zhu Zhuangrui, Zhang Jianrun. Study on Design for Structure and Size Optimization of Beam-sheet on Big Part in Machine Tool Based on APDL[J]. Light Industry Machinery, 2006, 24(4): 60-62.

[10]梅莉,孙智孝,姬鹏博,等. 基于拓扑和尺寸优化的翼肋类结构设计研究[J]. 飞机设计, 2013, 33(2): 8-12.

Mei Li, Sun Zhixiao, Ji Pengbo, et al. The Design Study of the Rib-Like Structure Based on Topology and Size Optimization[J]. Aircraft Design, 2013, 33(2): 8-12.

[11]邢晓辉,王洪川,王贵飞,等. 基于灵敏度分析的数控机床床身尺寸优化设计[J]. 组合机床与自动化加工技术, 2013(11): 5-8.

Xing Xiaohui, Wang Hongchuan, Wang Guifei, et al. Size Optimization Design of the Lathe Bed of CNC Machine Based on Sensitivity Analysis[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2013(11): 5-8.

[12]王晓煜, 贾振元, 杨帆, 等. 龙门加工中心横梁部件的拓扑优化设计与分析[J]. 制造技术与机床, 2009(11): 64-68.

Wang Xiaoyu, Jia Zhenyuan, Yang Fan, et al. The Topological Optimization of Design and Analysis for Gantry Machine Tool Crossbeam Component[J]. Design and Research, 2009(11): 64-68.

[13]Querin O M, Young V, Steven G P, et al. Computational Efficiency and Validation of Bi-directional Evolutionary Structural Optimization [J]. Computer Methods in Applied Mechanics and Engineering, 2000, 189(2): 559-573.

[14]荣见华, 姜节胜, 胡德文，等.基于应力及其灵敏度的结构拓扑渐进优化方法[J].力学学报, 2003, 35(5): 584-591.

Rong Jianhua, Jiang Jiesheng, Hu Dewen, et al. A Structural Topology Evolutionary Optimization Method Based on Stresses and Their Sensitivity[J]. Acta Mechanica Sinica, 2003, 35(5): 584-591.

[15]Chen Tingyu, Lin Chiayang. Determination of Optimum Design Spaces for Topology Optimization[J].Finite Elements in Analysis and Design, 2000, 36:1-16.

[16]荣见华, 姜节胜, 徐飞鸿,等. 一种基于应力的双方向结构拓扑优化算法[J].计算力学学报, 2004, 21(3): 322-329.

Rong Jianhua, Jiang Jiesheng, Xu Feihong, et al. A Bi-directional Algorithm of Structural Topology Optimization[J]. Chinese Journal of Computational Mechanics, 2004, 21(3): 322-329.

[17]荣见华,唐国金,杨振兴,等. 一种三维结构拓扑优化设计方法[J].固体力学学报, 2005, 26(3): 289-296.

Rong Jianhua, Tang Guojin, Yang Zhenxing, et al. A Three-dimension Structural Topology Optimization Design Method[J]. Acta Mechanica Solida Sinica, 2005, 26(3): 289-296.

[18]荣见华,姜节胜,颜东煌，等.基于人工材料的结构拓扑渐进优化设计[J].工程力学, 2004, 21(5): 64-71.

Rong Jianhua, Jiang Jiesheng, Yan Donghuang, et al. Evolutionary Optimization Design of Structural Topology Based on Man-made Material[J]. Engineering Mechanics, 2004, 21(5): 64-71.

[19]荣见华, 郑健龙, 徐飞鸿.结构动力修改及优化设计[M].北京：人民交通出版社,2002.

[20]孔文秦.连续体结构双向渐进优化方法研究[D].南京：南京航空航天大学, 2005.

(编辑苏卫国)

Topology Optimization of Large Crossbeam Based on Decomposition of Functional Sections

Wu FengheShi HongliangXu XiaopengFan Junwei

Yanshan University, Qinhuangdao, Hebei, 066004

Abstract:According to the poor readability of a three-dimensional structural topology optimization model for crossbeam with complex load conditions and the difficulty to get an effective guidance on structure optimization, a decomposition of the functional sections topology optimization method was proposed. Based on the principles of decomposition and equivalence of forces, the three-dimensional solid was decomposed into two-dimensional functional sections in three planes. The properties of resistance to bend or torsion were determined according the stress modes of each functional section; then the two-dimensional topology optimization of each of the two main functional sections was analyzed. The topology optimization of the three-dimensional solid might be accomplished by integrating the results of the analysis. At last, the goal that converting 3D topology optimization into 2D topology optimization might be completed. The crossbeam of turning-milling machining center CXK5463 was used as an example to verify the effect of the proposed method. The simulation results show that: a clear stress transfer path may be got, keeping the static and a dynamic characteristics of the crossbeam stable. The total weight is reduced by 12.67%. The results of the topology optimization are obvious and the helpful instruction and reference may be provided for the topology optimization of large-heavy complex machinery by this method.

Key words:topology optimization; crossbeam; functional section; finite element andysis(FEA)

收稿日期：2015-07-08

基金项目：国家科技重大专项(2013ZX04001-041)；国家自然科学基金资助项目(51405427)

中图分类号：TG542

DOI：10.3969/j.issn.1004-132X.2016.10.011

作者简介：吴凤和，男，1968年生。燕山大学机械工程学院教授、博士研究生导师。主要研究方向为数字化设计制造、智能制造。授权发明专利2项。发表论文60余篇。史红亮，男，1990年生。燕山大学机械工程学院硕士研究生。许晓鹏，男，1987年生。燕山大学机械工程学院博士研究生。范俊伟，男，1989年生。燕山大学机械工程学院硕士研究生。