基于目标规划法对众筹筑屋方案设计*

余国锋， 姚庆锋， 刘家保

(1.安徽工商职业学院 教务处，合肥 230041；2.安徽新华学院 公共课程部，合肥 230088)



基于目标规划法对众筹筑屋方案设计*

余国锋1， 姚庆锋1， 刘家保2

(1.安徽工商职业学院 教务处，合肥 230041；2.安徽新华学院 公共课程部，合肥 230088)

摘要：为了提高参筹者对各房型的满意度，在筑屋规划方案设计上，在满足容积率，各种房型建设范围等约束条件下，建立目标函数为参筹者对每种房型的满意度与房型所占比率的方差最小的非线性规划模型，并对分配方案进行了核算，得出方案下的投资回报率为20.9%；由于方案投资回报率不满足25%的要求，利用动态规划法重新改进方案；理论分析和计算结果表明，利用状态转移方程，动态调整房型套数，最终获得众筹筑屋最佳方案。

关键词：众筹筑屋； 优化； 动态规划； 层次分析法

1问题的提出

众筹(Crowdfunding)是一种大众通过互联网相互沟通联系，并汇集资金支持由其他组织和个人发起的活动的集体行动[1]。众筹筑屋是互联网时代一种新型的房地产形式，是地产互联网金融平台，使购房人有机会在土地阶段就参与房产项目众筹，获得定制化服务与更大的购房优惠空间。同时，房产开发商可以通过众筹大幅降低融资成本，并提前锁定了购房客户，降低项目的销售风险与销售成本。

现有占地面积为102 077.6 m2的众筹筑屋项目。项目推出后，有上万户购房者登记参筹。项目规定参筹者每户只能认购一套住房。在建房规划设计中，需考虑诸多因素，如容积率、开发成本、税率、预期收益等。根据国家相关政策，不同房型的容积率、开发成本、开发费用等在核算上要求均不同，相关条例与政策见附件[2]。

(1) 为了信息公开及民主决策，需要将这个众筹筑屋项目原方案(称作方案Ⅰ)的成本与收益、容积率和增值税等信息进行公布。请你们建立模型对方案I进行全面的核算，帮助其公布相关信息。

(2) 通过对参筹者进行抽样调查，得到了参筹者对11种房型购买意愿的比例。为了尽量满足参筹者的购买意愿，请你重新设计建设规划方案(称为方案Ⅱ)，并对方案II进行核算。

(3) 一般而言，投资回报率达到25%以上的众筹项目才会被成功执行。所给出的众筹筑屋方案Ⅱ能否被成功执行？如果能，请说明理由。如果不能，应怎样调整才能使此众筹筑屋项目能被成功执行？

2模型假设

(1) 假设此众筹项目的所有房型均被参筹者认购；

(2) 假设宏观经济波动对楼房的售价及销售率的影响不大；

(3) 对于增值税计算中所涉及的项目，以题目提供信息为准，合理忽略一些微小的因素；

(4) 对于附件中涉及的满意度调查，认定其合理性。

3房产相关指标核算

方案Ⅰ核算：问题要求对方案一进行全面的核算，以便对成本、容积率、增值税、收益等信息进行公布。

3.1成本(FC)

成本=各房型建设面积×单个房型套数×开发成本

开发成本(FC)=各房型建设面积(S)×

单个房型套数(Q)×

各房型开发成本(FC)

3.2容积率(PR)

容积率=总用地面积/总建设面积

容积率(PR)=总建筑面积(GFA)/总用地面积(K)

3.3增值税(VAT)

土地增值税的税率受增值额与扣除项目金额比例的影响，因此要计算增值税，必须要计算出增值额和扣除项目金额[3]。扣除项目金额：

总增值额(AV)=总收入(TM)-扣除项目金额(VC)

扣除项目金额分为以下方面：

房地产开发费用：按银行贷款利率5.25%计算；与转让房地产有关的税金：按转让房地产税率5.65%计算；其他扣除项目：按取得土地金额和开发成本的20%计算；在计算扣除项目金额时，要考虑到各房型的开发成本是否允许扣除，如房型3、房型8、房型11开发成本不允许扣除，则不加以计算。

增值额的计算依赖扣除项目金额，增值额等于收入减去扣除项目金额，得到增值额和扣除项目金额后，可以根据增值额和扣除项目金额的比例计算出增值税。

3.4收益(TR)

房地产的收益就是收入去除各种支出之后的纯利润；房地产的最终收益等于售房总收入减去成本投入和国家征收的土地增值税，总收益(TR)=总收入(TM)-总开发成本(TC)-总增值税(VAT)-取得土地使用支付金额(TA)。

4基于目标规划提高满意度的方案设计

4.1问题的分析

问题中要求根据11种房型最低套数约束和最高套数约束和参筹登记网民对各种房型的满意比例，重新设计一套尽量满足参筹者购买意愿的规划方案。

由于题目数据中没有明确的关于总建筑面积的规定，因此，总建筑面积须由题目提供的数据获取。

已知总建筑面积=容积率×总用地面积，由于总用地面积是固定的102 077.6 m2，所以只需确定规划方案的容积率即可求出总建筑面积。国家规定的最大容积率要求为2.28，在计算时，将容积率固定为最大容积率，即规划方案二的容积率固定采用最大容积率，此时，能够得出最大建筑面积为2.28×102 077.6=232 736.928 m2。

由于在几种房产类型中，房型9、10、11三种房型不列入容积率的计算，所以，以上求得的最大建筑面积为房型1到房型8的建筑面积。

通过对参筹登记网民对各种房型的满意比例的分析，以及问题中“为了尽量满足参筹者的购买意愿”的要求，决定在方案的规划过程中采用最优化的方法，忽略对收益的关注与分析，完全立足于对参筹者的购买意愿的分析，尽量多的满足参筹者的购买需求(图1)。

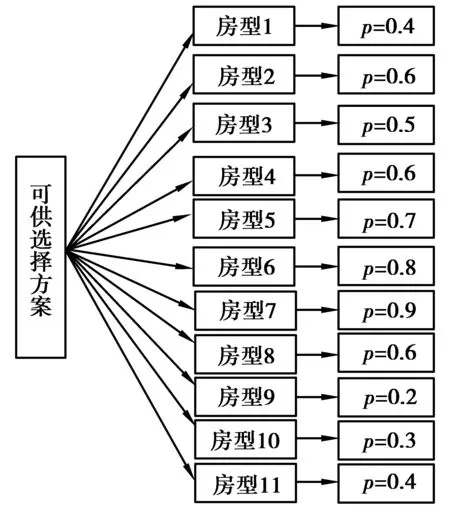
图1　对各房型调查满意度Fig.1　Satisfaction with each type of the houses

4.2基于层次分析法(AHP)对各房型满意度的构建

(2) 求比较判别矩阵的特征值和特征向量。利用Matlab软件编程[5]计算得到A矩阵的最大特征值λ=11.232对应的权向量(归一化)

ω=(0.07,0.10,0.09,0.10,0.12,0.14,

0.15,0.10,0.03,0.05,0.07)T

(3) 模型的一致性检验。定义一致性指标：

为衡量CI的大小，引入随机一致性指标RI(表1)。

表1　随机一致性指标

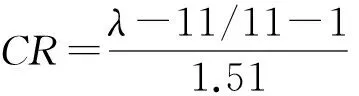
(4) 计算满意度的最终结果为

ω=(0.07，0.10，0.09，0.10，0.12，0.14，

0.15，0.10，0.03，0.05，0.07)T

4.3基于提高满意度的分配方案的规划

根据各种房型满意度的调查结果分析，要提高满意度，在满足容积率一定的前提下，各种房型所占的比率应与各房型的满意率保持一致，故模型利用每种房型满意率与对应房型所占比率的方差最小，构建非线性规划模型。

设xi为选择第i套房型的套数

现建立如下规划方程

利用Lingo程序计算[6]，可得：

x1=123;x2=177;x3=159;x4=177;x5=210;x6=213;

x7=267;x8=177;x9=51;x10=89;x11=123

4.4对方案进行核算

(1) 成本(FC)：成本(FC)=各房型建设面积(S)×单个房型套数(Q)×开发成本(FC)，FC=1 179 194 384元。

(2) 容积率(PR)：在方案Ⅱ的规划中使用国家规定最大容积率容积率(PR)=2.28

(3) 收益(TR)：

总收益(TR)=总收入(TM)-总开发成本(TC)-

总增值税(VAT)-

取得土地使用支付金额(TA)

总收入(TM)=2 899 530 800元

总开发成本(TC)=1 179 194 384元

总增值税(VAT)=674 855 857.4元

取得土地使用支付金额(TA)=777 179 627元

总收益(TR)=268 300 931.6元

(4) 投资回报率(TZ)：

投资回报率(TZ)=总收益(TR)/[总成本(TC)+

取得土地使用支付金额(TA)]

投资回报率(TZ)=20.902%<25%

5基于动态规划法对模型二的改进

5.1动态规划法的基本思想

一般来说，只要问题可以划分成规模更小的子问题，并且原问题的最优解中包含了子问题的最优解，则可以考虑用动态规划解决。动态规划的实质是分治思想和解决冗余，因此，动态规划是一种将问题实例分解为更小的、相似的子问题，并存储子问题的解而避免计算重复的子问题，以解决最优化问题的算法策略。由此可知，动态规划法与分治法和贪心法类似，它们都是将问题实例归纳为更小的、相似的子问题，并通过求解子问题产生一个全局最优解。其中贪心法的当前选择可能要依赖已经作出的所有选择，但不依赖于有待于做出的选择和子问题。因此贪心法自顶向下，一步一步地作出贪心选择；而分治法中的各个子问题是独立的(即不包含公共的子问题)，因此一旦递归地求出各子问题的解后，便可自下而上地将子问题的解合并成问题的解[7]。

解决上述问题的办法是利用动态规划。对于问题，由于上述模型二分配方案不满足投资回报率条件，现对模型二采用动态规划法进行改进，以模型二中各种房型套数作为初始条件，通过搜索，对收益率最高的房型首先增加套数，收益率最低的房型减少套数，利用容积率约束条件，得出一组方案，检验是否满足投资回报率要求，如果不满足，重新搜索，以此类推，一直到搜索出满足条件为止。

5.2模型的建立

(1) 模型的构建。记第k种方案下每种房型套数为xki(i=1,2,…,11)。

状态变量：将Bk(xk1,xk2,…,xk11)定义为在第k种方案下的投资回报率；

决策变量：记十一维向量Fk=(xk1,xk2,…,xk11)定义为在第k种方案下一种投资房型套数组合。

(2) 状态转移方程：

最优指标：Bk(xk1,xk2,…,xk11)≥25%。

动态规划法正是求解多步决策的有效方法。它要求把求解的问题一层一层地分解成一级一级、规模逐步缩小的子问题。直到可以直接求出其解的子问题为止。分解成所有子问题按层次关系构成一棵子问题树，树根是原问题。原问题的解依赖于子问题树中所有子问题的解。

5.3模型求解

穷举法：计算机编程，先建立编程的基本过程，然后考虑模型图2，再编写程序。

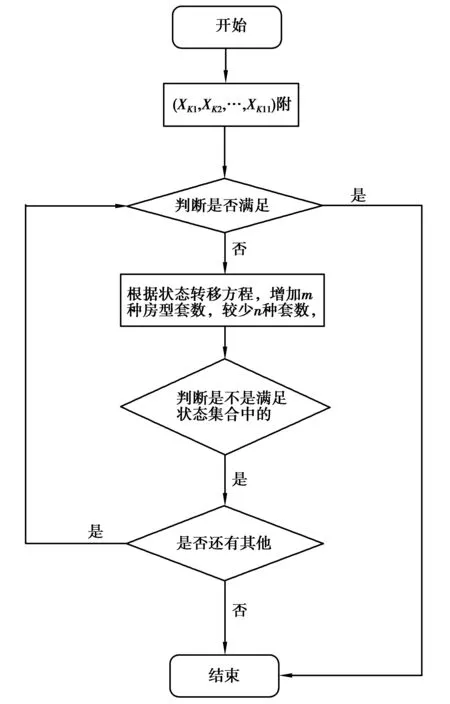
图2　穷举法示例Fig.2　Example of exhaustion method

即就可以得出结果如表2。

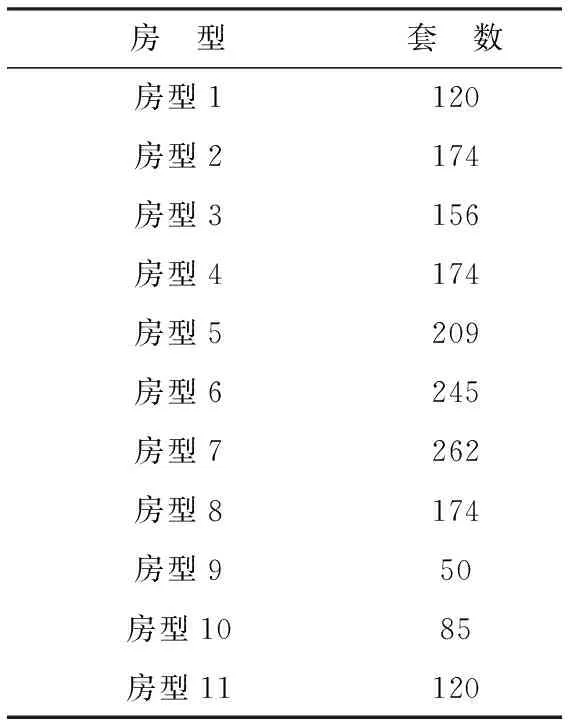
表2　规划方案Ⅲ

5.4 规划方案Ⅲ核算

规划方案Ⅲ经过计算，能够得到总开发成本(TM)=1 408 158 299元，总增值税(VAT)=871 274 093.1元，总收益(M)=635 700 202元，投资回报率(TZ)=25.979%。

6模型的评价与推广

6.1模型的优点

(1) 问题二，三中采用目标规划的方法，能让所得出的结果一目了然。

(2) 在每种方案的核算中，既考虑了单一因素，又考虑了众多其他因素，考虑较为全面。

(3) 模型建立的思路清晰、合理，模型建立的方法简单，对每种因素都清晰的反映出来。

(4) 模型现实意义较强，可反映现实房地产相关情形。

6.2模型的缺点

(1) 所采用的模型较为简单，也使得众多的因素未能考虑进去。由于影响房地产核算的因素众多、数据难以收集完全等，但由于这些因素对问题分析的因素较小，如果考虑周全，必然会让问题复杂化，不易讨论问题结果。

(2) 在每种方案的计算中，众多因素间耦合性较大，变量取值范围较广，因此在计算成本、税收等核算指标上存在一定误差。

6.3模型的推广

规划问题在解决生产组织等系统中，都发挥着重要的作用，关系分析可将各类影响因子放入规划模型中，可以通过相关计算软件得到兼顾全局的最优解。模型的求解是一个典型的规划问题，虽然只是解决了众筹筑屋方案设计，但却可以广泛的适用于目前的资金存贷、证券交易等金融领域的投资行为，对如何使用资金做出指导。

参考文献(References)：

[1] ORDANINI A，MICELI L，PIZZETTI M.Crowd-funding:Transforming Customers into Investors Through Innovative Service Platforms[J].Journal of Service Management,2011,22(4):125-134

[2] 李明会.房地产税改的难点、步骤及深层次问题综述[J].重庆工商大学学报(自然科学版)，2007，17(1)：13-17

LI M H.Review of Difficulties,Procedure and Deep Problems in the Reform of Real Estate Tax[J].Journal of Chong-qing Technology Business University(Natural Science Edition),2007，17(1)：13-17

[3] 储敏.层次分析中判断矩阵的构造问题[D].南京:南京理工大学,2005

CHU M.Structure of Judgment Matrix in Analytic Hierarchy Process[D].Nanjing:Nanjing University of Science and Technology,2005

[4] 刘会灯，朱飞.Matlab编程基础与典型应用[M].北京：人民邮电出版社，2008

LIU H D,ZHU F.Matlab Programming Basis and Typical Application[M].Beijing:People’s Posts and Telecom-munications Press,2008

[5] 谢金星.优化建模与LINDO/LINGO软件[M].北京：清华大出版社，2009

XIE J X.Optimization Modeling and LINDO/LINGO Soft-ware[M].Beijing:Tsinghua University Press,2009

[6] 景崇毅,李玉萍,张杰.动态规划方法在项目投标决策中的应用研究[J].工业工程,2007,10(1):130-133

JING CH Y,LI Y P,ZHANG J.The Application Study of Dynamic Programming Method in Project Bid Decision-making[J].Industrial Engineering Journal,2007,10(1):130-133

[7] 韩中根.数学建模实用教程[M].北京：高等教育出版社，2012

HAN ZH G.Practical Tutorial on Mathematical Modeling[M].Beijing:Higher Education Press,2012

责任编辑：田静

Design of Crowd-Funding House Building Based on Goal Programming

YU Guo-feng1, YAO Qing-feng1, LIU Jia-bao2

(1.Academic Affairs Office, Anhui Business Vocational College, Hefei 230041, China；2.Department of Public Courses, Anhui Xinhua University, Hefei 230088, China)

Abstract：In order to enhance the funders’ satisfaction with the house type, based on the constraints, including house-building plan design, satisfying the rate of capacity and the scope of house-building types, this paper uses nonlinear programming method to build the objective function, measures the calculated allocation scheme, and obtains the investment return rate of 20.9%. Due to the rate lower than 25%, the plan is redesigned by dynamic programming method. The results of theoretical analysis and computation show that the best plan of funders house-building will be gained by using the state transition equation and dynamic adjustment of houses sets in different types.

Key words：crowd-funding house building; optimization; dynamic programming; Analytic Hierarchy Process (AHP)

中图分类号：O29

文献标志码：A

文章编号：1672-058X(2016)03-0082-06

作者简介：余国锋(1980-)，男，安徽潜山人，讲师，硕士研究生，从事运筹与决策、数学模型研究.

*基金项目：安徽省重大教学改革研究项目(2013ZDJY191)；安徽省高等学校自然科学基金项目(KJ2013B105).

收稿日期：2015-10-28；修回日期：2015-12-07.

doi:10.16055/j.issn.1672-058X.2016.0003.017