信息粒化的SVR组合模型在季度GDP中的应用*

张　鹏

(太原工业学院 理学系，太原 030008)



信息粒化的SVR组合模型在季度GDP中的应用*

张鹏

(太原工业学院 理学系，太原 030008)

摘要：针对GDP未来一段时间的变化范围及走势进行预测，提出了信息粒化算法与支持向量回归机算法相结合的时间序列组合预测模型；以1994年第1季度到2013第4季度GDP值模糊粒化处理，对3个模糊参数Low、R、Up，通过交叉实验训练寻找支持向量回归机的最优参数，并进行回归预测，得出GDP在2014年各季度的变化范围与走势，与实际比较相吻合，说明算法具有良好的泛化性，能够作为时序数据的预测模型。

关键词：信息粒化；支持向量回归机； GDP

国内生产总值(GDP)指一个国家或地区在某时期内生产的所有最终物品和劳务的市场价值，是目前反映经济发展状况的重要指标。准确预测GDP的未来走势，对于经济研究、管理、决策等具有重要意义，然而GDP受很多不确定因素影响，虽很难做到预测准确值，但是GDP未来走势及变化范围还是能得到较好的预测。近来热门的人工智能算法如人工神经网络、灰色系统、粗糙集、小波分析、遗传算法等，具有自我适应、自我学习、自我组织优点，很大程度上适合应用于经济数据问题上，诸多学者亦对此做了很多研究[1-5]。

信息粒化算法是将整体分解成若干部分进行研究，其中每个部分称为一个信息粒，本质就是一些相关元素的集合。支持向量回归机(SVR)能够较好的解决样本小、非线性及避免陷入局部最优的数据情形，并且具有良好的泛化能力。首先通过构建粒空间获取一系列信息粒，然后SVR在单个信息粒上学习，最后通过交叉验证得出SVR最优参数，模型能较为准确分析出季度GDP未来变化趋势，为经济决策提供一定的支撑作用。

1信息粒化

1979年，Lotfi A.Zadeh[5]首次提出了信息粒的概念，将一组具有相似特征的研究对象作为一个整体来研究或将将一个整体作为一个部分来研究，主要有粗糙集信息粒化、模糊集信息粒化、熵空间信息粒化三大理论，其中，模糊信息粒是以模糊集形式表示的信息粒，而信息粒为一些具有相似特性或难以区分的元素所组成的集合。其对时间序列进行模糊粒化可分为两步：窗口化和模糊化，其中窗口化是将整体时间序列分割成若干子序列，也成为窗口划分；模糊化则是将单个子窗口进行模糊化,生成若干模糊集，也称为f—粒化过程。

考虑整体时间序列X，将其作为一个窗口进行模糊化,模糊化的任务是在X上建立一个模糊粒子P,即构造一个能够合理描述X的模糊概念G(以X为论域的模糊集合),确定了G也就确定了模糊粒子P[6]:

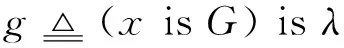
(1)

其中，x是论域U中取值的变量，G是U的模糊子集，由隶属函数A来刻画。λ表示可能性概率。一般假设U为实数集，G为U的凸模糊子集，λ是单位区间的模糊子集。综合考虑模糊粒子既要为体现某种特性，又能充分代表原始数据，可构建如下关于A的一个函数:

(2)

其中,MA表示原始数据，NA表示粒子的特性。

常用的模糊法有梯形、三角型、高斯型、抛物型等形式。选用三角型模糊粒子，其隶属函数为如下分段函数:

(3)

其中，Low表示原始时序最小值，R表示平均值，Up表示最大值。

2支持向量机

1995年由Vapnik首先提出支持向量机，其具有小样本性、鲁棒性、全局优等特点，之后被广泛应用于模式识别中。支持向量机通过非线性映射将低维空间映射至高维空间，将搜索到的最优超平面问题转化为二次凸规划问题。假设在高维特征空间构建线性回归模型为

(4)

其中φ(x)为非线性映射函数。

定义ε线性不敏感损失函数：

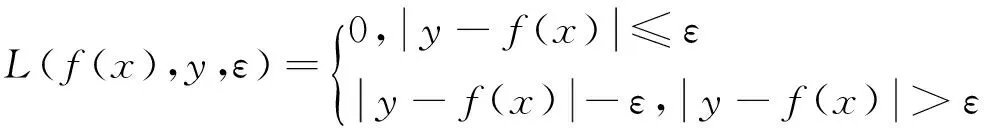
(5)

其中f(x)为预测值，y为真实值。

从而，回归问题转换为如下二次凸规划问题：

(6)

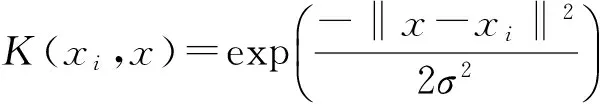
3构建模糊信息粒化支持向量机的GDP组合预测模型

模糊粒化的支持向量机组合预测模型流程如下：

(1) 搜集1994—2014年各季度GDP数据；

(2) 对时序数据进行三角型模糊信息粒化处理；

(3) 对SVR进行训练确定并优化确定最优参数c和g；

(4) 利用优化SVR模型对2014第一季度至第四季度GDP进行预测检验。

4实证分析

数据来源于中国统计局官网http://data.stats.gov.cn/，以1994年第一季度至2014年第4季度GDP值为研究对象，其中2013年第4季度前的数据用于训练模型，之后4个季度的数据用于模型检验。1994—2014年GDP变化整体呈上升态势，走势曲线见图1。

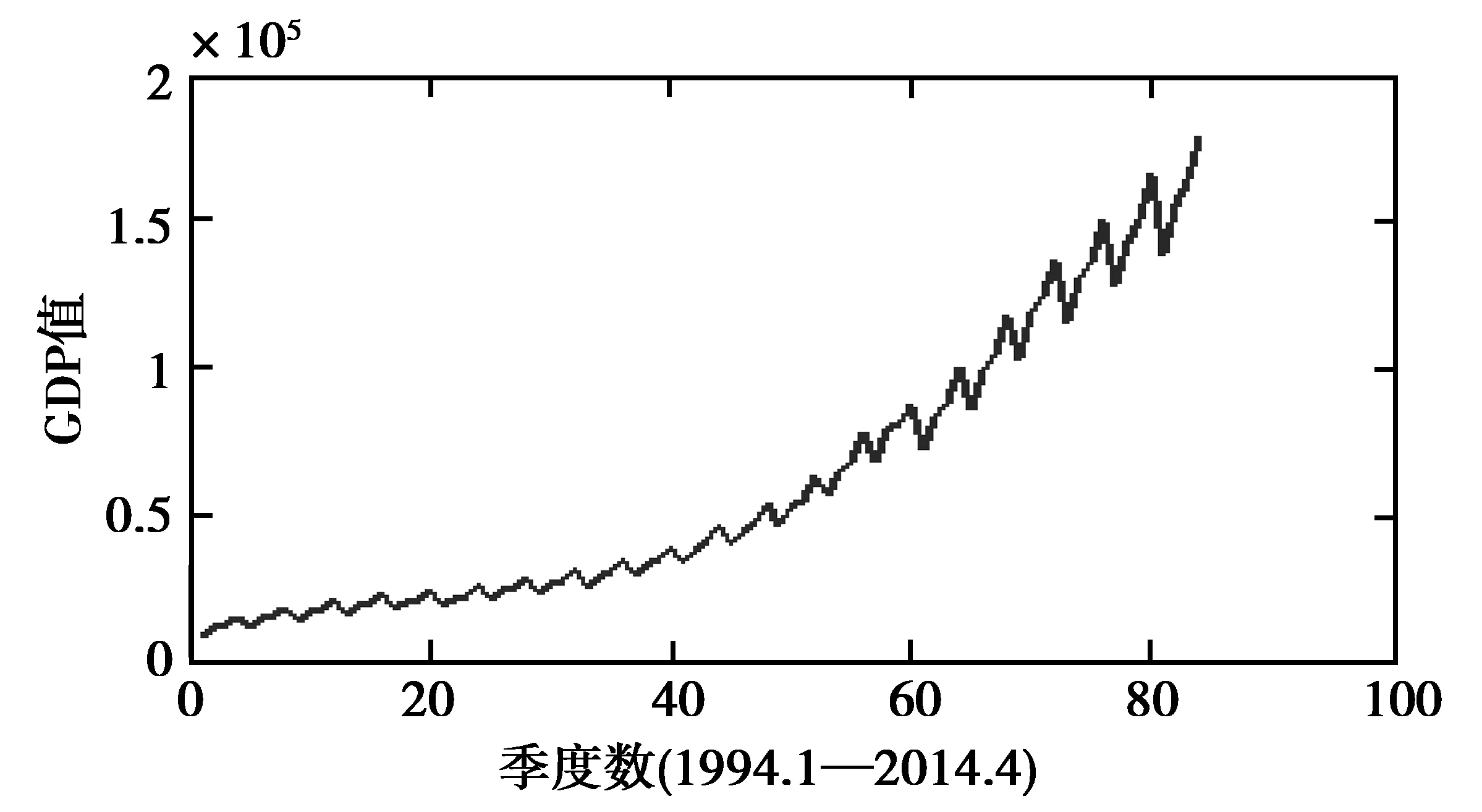
图1　1992—2014年季度GDP走势曲线Fig.1　Seasonal GDP tendency curve from 1994 to 2014

4.1原始数据模糊信息粒化预处理

训练数据共计84个季度的GDP值，将4个季度的GDP作为一个窗口，按照模糊粒化思想得窗口数目为21，进而将原始GDP数据模糊粒化为Low、R、Up三个参数，其分别代表GDP值变化的最小值、平均值和最大值。在Matlab2013a 环境下进行模糊粒化处理结果见图2。

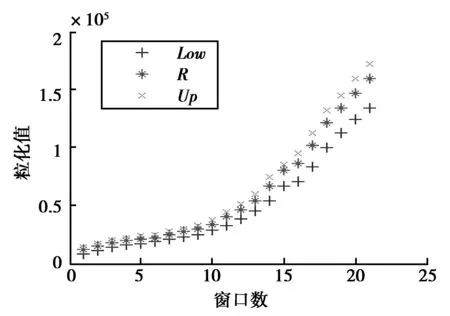
图2　原始数据模糊粒化散点图Fig.2　Fuzzy granulation of original data

4.2利用SVR 对模糊粒化数据进行回归

4.2.1参数寻优

对3个模糊粒子Low,R,Up分别进行SVR回归分析，首先利用极差归一化方法将数据转化至[0,1]范围，然后采用交叉验证寻找分别SVR最优参数，最后进行训练和检验。Low、R、Up分别进行交叉验证后对应的SVR最优参数如表1。

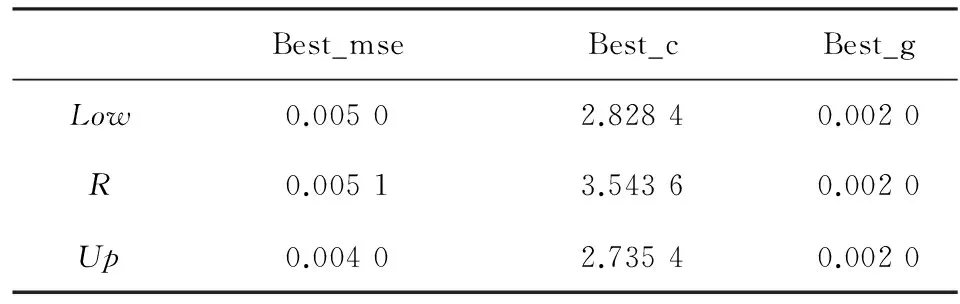
表1　三个参数对应SVR的最优参数

4.2.2参数SVR拟合

利用最优参数分别对3个参数Low、R、Up进行拟合，结果如图3。

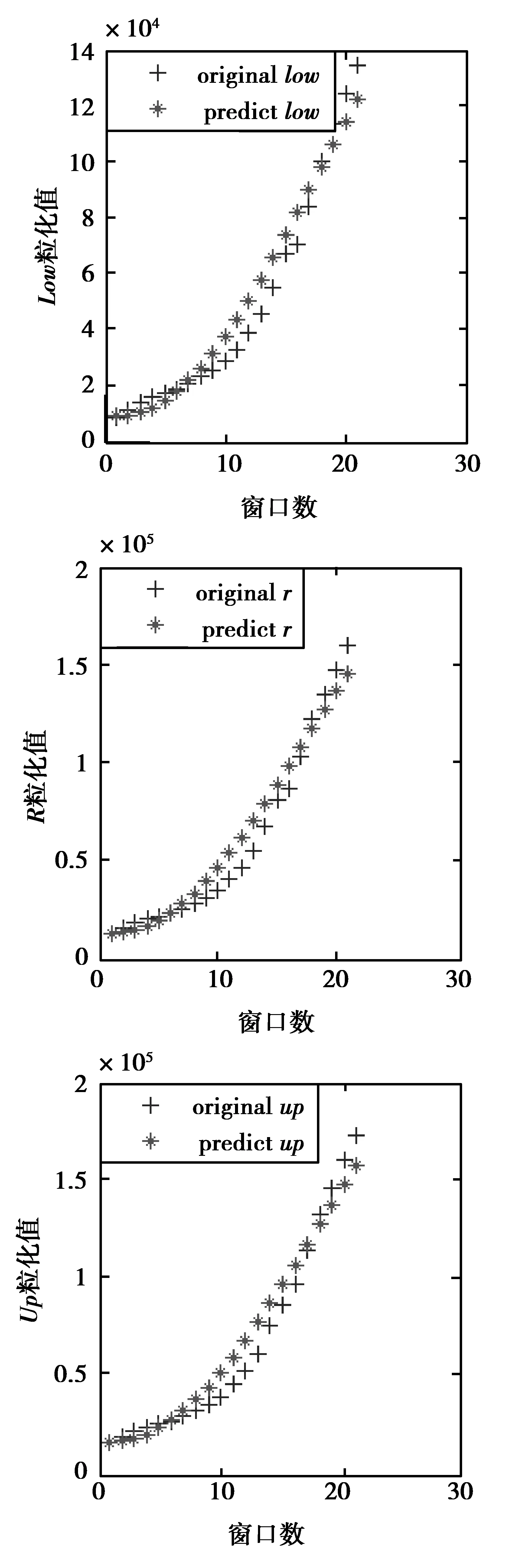
图3　Low、R、Up进行SVR回归拟合值与真实值比较Fig.3　Contrast between SVR regression fitting value and real value

4.3利用最优SVR进行预测

利用建立的模型预测2014年4个季度的GDP最小值、平均值及最大值(表2)。

表2　预测值与真实值比较

由表2可知预测的GDP变化范围是相对准确的，并且可分析出2014年4个季度的GDP值稳步上升。表明模型预测效果具有可靠性，能够为相关部门决策提供一定的支撑作用。

5结论

(1) 影响GDP有很多不确定性和随机波动因素，预测难度较大，基于模糊粒子处理与SVR相结合的组合算法，以季度GDP数据为例，预测结果变化范围及变化趋势与实际在一定程度上吻合，表明组合模型具有一定的适用性。

(2) SVR时序回归模型仍存在一定的不足。参数c和g的寻优算法还能进一步优化，从而进一步提高模型预测的准确性和稳定性。

参考文献(References)：

[1] 王莎莎,陈安,苏静,等.组合预测模型在中国GDP预测中的应用[J].山东大学学报,2009(2)：108-112

WANG SH SH,CHEN A,SU J.Application of the Combination Prediction Model in Forecasting the GDP of China[J].Journal of Shandong University,2009(2):108-112

[2] 宣平.基于灰色BP网络的GDP总量组合预测模型应用研究[J].黄山学院学报,2009(1)：27-29

XUAN P.A Combined Prediction Model Based on Grey Artificial Neural Network and Its Application[J].Journal of Huangshan University,2009(1):27-29

[3] 孙彩,姜明辉.基于GP的非线性GDP预测模型的构建与应用[J].哈尔滨工业大学学报,2008(4)：89-93

SUN CH,JIANG M H.Constructionand Application of Non-linear GDP Forecast Model Based on GP[J].Journal of Hit,2008(4):89-93

[4] 熊伟丽，徐保国.基于PSO的SVR参数优化选择方法研究[J].系统仿真学报，2006(3):207-211

XIONG W L,XU B G.Study on Optimization of SVR Parameters Selection Based on PSO[J].Journal of System Simulation,2006(3):207-211

[5] 耿鹏,齐红倩.我国季度GDP 实时数据预测与评价[J].统计研究，2012(4):302-318

GENG P,QI H Q.Forecasting and Assessment of China’s Quarterly Real-time GDP[J].Statistical Research,2012(4):302-318

[6] ZADEH L A.Fuzzy Sets and Information Granularity[G]∥Advances in Fuzzy Set Theory and Applications,Amsterdam Holand,1979

责任编辑：田静

Application of SVR Combined Model with Information Granulation to Quarterly GDP

ZHANG Peng

(Science Department, Taiyuan Institute of Technology, Shanxi Taiyuan 030008, China)

Abstract：In order to predict GDP change and trend in a period of future, this paper proposes time series combination forecast model based on the combination of information granulation algorithm and support vector regression machine algorithm, makes fuzzy granulation processing on the GDP values from the first quarter of 1994 to the forth quarter of 2013, uses cross-over experiment training to seek the optimal parameter of support vector regression machine and conducts regression forecast based on three fuzzy parameters such as Low, R and Up and obtains GDP change and trend in each quarter of 2014 which is identical to the practice. The results show that this algorithm has good generalization and can be used as prediction model for time series data.

Key words：information granulation; support vector regression machine; GDP

中图分类号：F222；O159

文献标志码：A

文章编号：1672-058X(2016)03-0066-04

作者简介：张鹏(1989-)，男，山西平顺人，助教，硕士研究生，从事应用统计研究．

*基金项目：太原工业学院青年科学基金(2015LQ20).

收稿日期：2015-10-09；修回日期：2015-11-03.

doi:10.16055/j.issn.1672-058X.2016.0003.014