三种给药方式的微分方程及函数性态比较探讨

王莲招（厦门医学高等专科学校，福建　厦门　361008）

三种给药方式的微分方程及函数性态比较探讨

王莲招
（厦门医学高等专科学校，福建厦门361008）

摘要：建立数学模型，揭示医药学中各变量之间的数量关系，用数学思想方法解决问题，已成为现代医学发展的潮流。微分方程是建立数学模型的一个重要工具。函数是描述变量间相互联系的一种数学模型，用于表达变量间相互依赖关系的基本数学形式。研究函数的性态可以更好了解其变化规律，帮助指导解决一些医药学问题。本文列表比较一室模型中三种给药方式的微分方程，并用极限、导数、定积分等微积分数学工具对相应函数的性态进行分析探讨，梳理三种给药方式血药浓度变化规律。

关键词：微分方程；函数；性态；血药浓度

随着科学技术的飞速发展，医药学的发展日趋精确化和解析化，亟需利用数学方法解决医药学中发现的问题。由定性描述转向定量化分析，揭示医药学中的数量规律性已成为一种趋势。微分方程在医药学的应用也越来越引起人们的关注和重视。药物动力学是运用动力学原理和数学方法，研究药物、毒物及代谢物在机体内吸收、分布、代谢和排泄过程定量规律的科学。一室模型假定身体是由一个房室组成，给药后药物立即均匀分由于整个房室，并按一级速率过程从该室中排泄出去。不同的给药方式药量在体内的变化有不同的规律、不同的效果。血药浓度变化规律是药物动力学中重要的问题。下面就最简单一室模型中三种给药方式（快速静脉注射、恒速静脉滴注、血管外给药）的微分方程和函数性态及血药浓度变化情况列表比较探讨。

一、微分方程模型及函数[1]

设D0为给药剂量，D(t)为t时刻体内的药物量，c(t)为t时刻体内的药物浓度，vd为药物的表观分布容积，k为一级消除速率常数。假设药物在体内的分布符合一室模型，且按一级速率过程从体内消除，根据动力学模型及药物在体内的变化符合级速率过程的微分方程表示为：可以建立以下三个微分方程（组），解微分方程的初值问题可得药量随时间的变化关系。再将D(t)除以表观分布容积，得到体内血药浓度随时间变化关系。如表1所示。

三种函数都与指数衰减模型函数y=A·ax（其中0＜a＜1）有关。药物衰变规律公式C=C0·e-kt在医学上称为药物动力学一级反应公式。用它可以研究药物的衰变规律。

二、函数图像的性态分析

函数的作图可以借助计算机作图软件或有绘图功能的函数型计算器等工具，（例如表2中的图象）。下面利用导数判断三种血药浓度函数图像（称为药时-曲线）的性态：有界性、单调性、凹凸性、极值、最值、拐点、渐近线等，如表2所示。

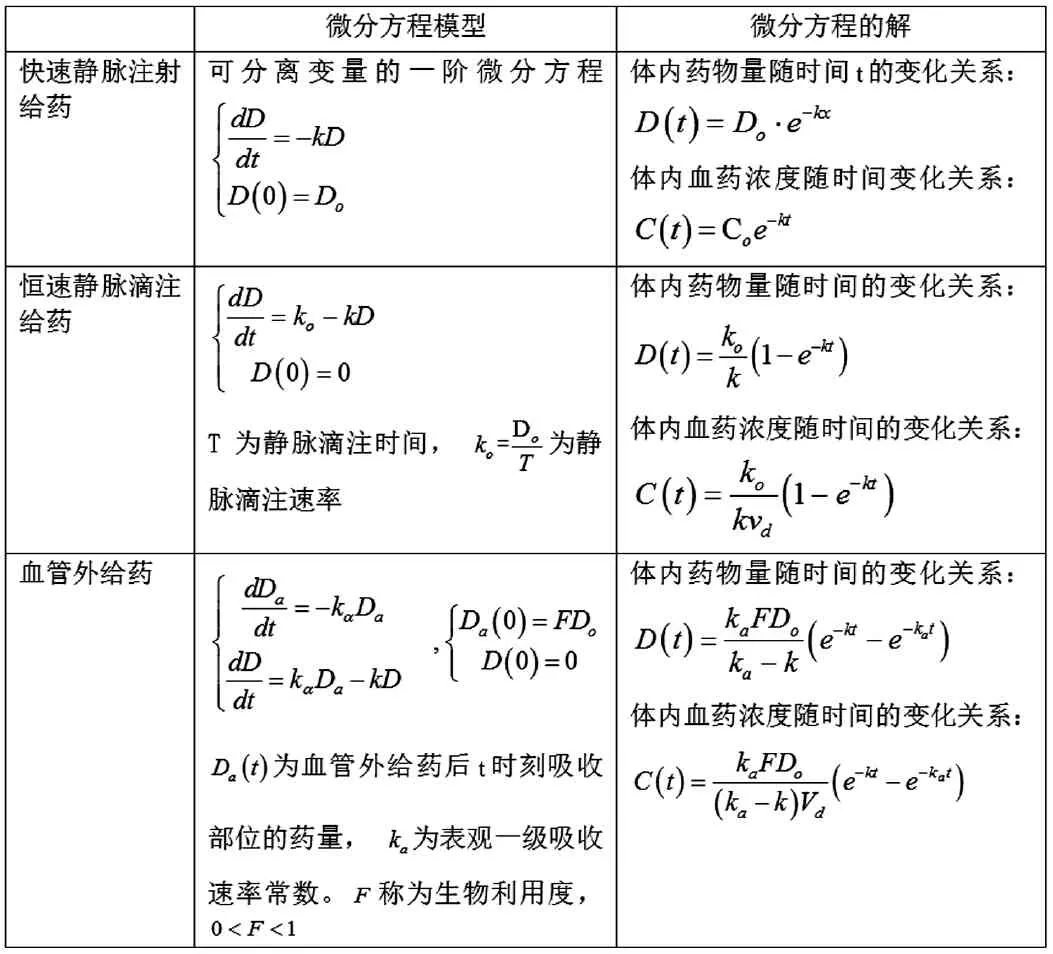
表1

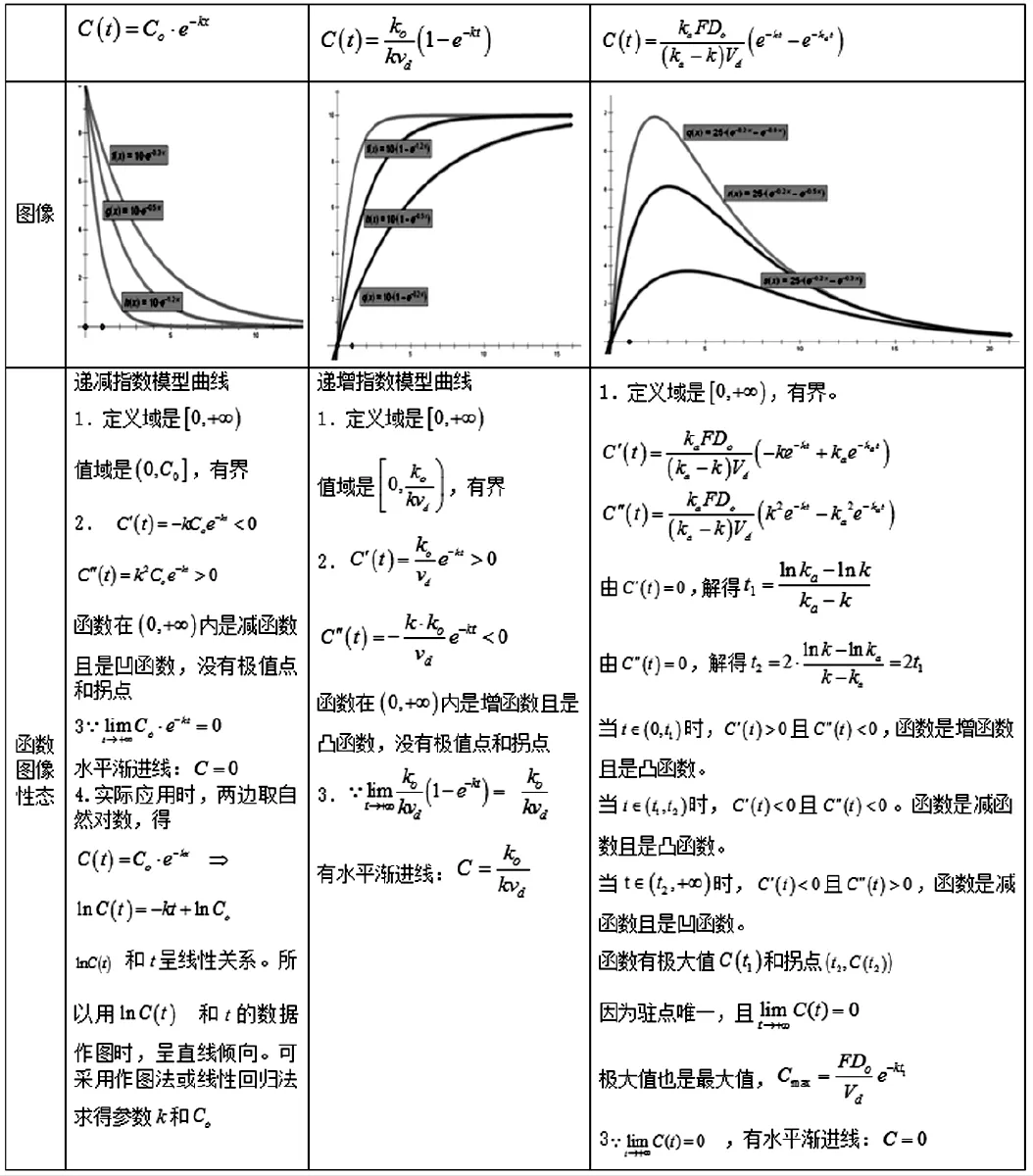
表2　

三、体内血药浓度变化情况

观察表2中三种给药方式的药时-曲线图像的性态特征，可以很直观看出三种给药方式体内的血药浓度的有不同的变化过程。如表3所示。

四、典型例题举例[2]

例1.用某药物进行静脉注射，其血药浓度下降是一级速率过程。第一次注射后，经过一小时后浓度降至初始的，求半衰期。

分析：设t时刻血药浓度为，c=c(t)，c(0)=c0

由已知得：

解得，C=C0e-kt把已知条件代入，可得ln2，根据表3可得半衰期为。也就是第一次注射后要使体内浓度不低于初始浓度的一半，经过2小时要进行第二次注射。

例2.已知n次静脉注射某药后，血液浓度的最高水平和最低水平分别为

表3　

例3.口服一定剂量的某种药物后，其血药浓度C与时间的的关系是C(t)=40(e-0.2t-e-2.3t)，问为何值，血药浓度最高，并求出最高浓度。

分析：C'(t)=40(-0.2e-0.2t+2.3e-2.3t)，由C'(t)=0，可解得t=因为是唯一驻点，所以当t=1.1630时，C有最大值Cmax⋍28.9423。

以上对药物动力学中最简单的一室模型中三种给药方式函数性态进行对比总结。药物治疗中，治疗作用与血液浓度密切相关。药时-曲线的性态直观精准地反映出了不同给药方式的血药浓度在不同时段的变化情况，对了解药效的强弱、吸收的快慢及生物利用度等参数有重要的指导作用，为科学准确判断、分析解决医药学中最优化和有效性问题提供了根据，例如口服或肌注一定剂量的某种药物后，血药浓度何时达到最高值？为获得理想的稳定血药浓度，怎样控制静脉滴注速度？病人需要多次给药，如何确定给药间隔时间才能达到和维持有效的血药浓度？等等。随着科学技术的飞速发展，高等数学成为医学领域不可或缺的定量分析工具，为医药学科研究提供精确的数据和可靠的指导。但药物在体内的动态变化过程相当复杂（如二室模型、多次给药情况等），还需要更多高等数学知识方法综合运用才能更好解决医学问题，因此在医用高等教学中教学要结合医药学实际问题，实施问题驱动，加强数学建模能力的训练和运用数学方法的意识，培养学生科学创新研究精神和定量分析的思维方法，提高分析问题和解决问题的能力。

参考文献

[1]顾作林.高等数学[M].北京：人民卫生出版社，2011.

[2]吴赣昌.医用高等数学[M].北京：中国人民大学出版社，2012.

Abstract:To establish mathematical model which reveals the quantitative relation between the variables in the medicine and to solve some problems by mathematic thinking have formed the trend of the development of modern medicine. Differential equation is an important tool for the establishment of a mathematical model while its function is a mathematical model describing the interrelation between the variables. The research on function condition may help understand the change rule, which guides to solve some problems in medicine. This paper compares the differential equations of three drug delivery methods in one room model, explores the properties of the corresponding functions by means of the limit, derivative, definite integral, etc. and analyzes the change law of blood concentration of the three drug delivery methods.

Keywords:differential equation; function; condition; blood concentration

中图分类号：O175

文献标志码：A

文章编号：2096-000X（2016）05-0111-03

作者简介：王莲招（1964-），女，福建龙海人，高级讲师，从事数学教育工作。