基于动力特性的简支U形梁的模态识别

周　奎,　缪润翰,　郭　耀,　刘　义

(上海理工大学 环境与建筑学院,上海　200093)



基于动力特性的简支U形梁的模态识别

周奎,缪润翰,郭耀,刘义

(上海理工大学 环境与建筑学院,上海200093)

摘要：基于自然激励技术(NExT)和ITD法的基本理论,采用环境激励的动力测试方法和基于S变换的滤波技术,对实验室3根1∶10缩尺比例的预应力混凝土U形梁进行了动力测试试验.通过提取分析模态参数,从模态识别的角度分析了采样频率、主梁腹板翼缘损伤、外荷载的激励对U形梁动力特性的影响.

关键词：U形梁; 环境激励; S变换; 模态识别

预应力混凝土U形梁是一种新型预应力混凝土桥梁结构,由道床板、主梁及端横梁等部分组成[1],属于下承式槽形梁结构,与箱梁、T梁及板梁等普通梁式构件相比,具有建筑高度低、降噪效果好、断面空间利用率高、行车安全、外形美观、施工形式多样及综合造价低等优点[2].现已建成的预应力混凝土U形梁主要有简支梁和连续梁两种结构形式,通常采用纵向、横向双向预应力体系[3],采用高强混凝土,设计使用年限为100年,分为25,30,35 m这3种标准跨径.

目前有关U形梁静力性能方面的研究较多,而基于其振动特性的动力性能方面的研究较少.因此，本文通过试验制作3根1∶10缩尺的预应力混凝土U形梁,结合NExT-ITD法和基于S变换的滤波技术,在环境激励条件下,从模态识别的角度分析采样频率、翼缘损伤、不同外荷载的激励对U形梁动力特性的影响.

1自然激励技术(NExT)和ITD法

自然激励技术(natural excitation technique,NExT)[4]是一种利用环境激励获得系统脉冲响应的有效方法,其基本思想是:在激励近似满足Gauss白噪声的条件下,结构中两点位移的互相关函数的表达式与脉冲响应函数形式相似,它们都能表示成一系列衰减的正弦函数之和[5].求得信号间的互相关函数后,可以运用时域模态参数识别方法识别系统的模态参数.

ITD法(ibrahim time domain technique)[6]是Ibrahim于1970年提出的,该方法的基本思想是:由于多自由度线性粘性阻尼系统的自由衰减响应可以通过其各阶模态的叠加来表示,根据测得的自由衰减响应信号进行3次不同延时采样,构造采样数据的增广矩阵,即自由衰减响应数据矩阵,并由响应与特征值之间的复指数关系建立特征矩阵,求解特征值问题,得到数据模型的特征值和特征向量,再根据模型特征值与振动系统特征值的关系,求解出系统的模态参数[7-8].

NExT-ITD法的具体识别流程分为以下几个步骤[9]:

a. 选择合适的参考点;

b. 计算各采样点与参考点的互相关函数;

c. 针对采样的延时时间Δt,通过延时法对互相关函数构造虚拟采样点;

d. 选取合适的互相关函数,构造采样数据的增广矩阵X;

f. 构造特征矩阵,求解特征值和特征向量;

g. 剔除虚假模态从而获得结构的模态参数.

2基于S变换的滤波技术

信号在产生、传输及处理的过程中,都不可避免地受到不同程度的噪声干扰,对信号的后续分析处理、判断及识别工作将产生严重影响[10].基于S变换的滤波技术[11-12]可以提取信号在某一时间段和频带内的特定信号分量,得到信号不同频率成分在各个时刻的振幅谱.

通常,信号可以表示为

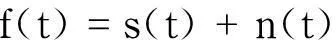
(1)

式中:s(t)为原始信号函数;n(t)为噪声函数.

根据S变换的叠加性,信号f(t)经广义S变换后为

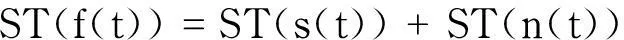
(2)

对信号进行去噪处理,使得ST(n(t))一项为0,保留有效信号,经过S逆变换映射到时间域即可得到滤波后的结果.

3预应力混凝土U形梁动力测试

3.1试件设计

试件为外形与标准U形梁相似的3根3m长的预应力混凝土梁,编号分别为PC-1,PC-2,PC-3,如图1所示.其中,梁PC-3由于混凝土浇筑过程中振捣不密实以及起吊过程中梁发生偏斜,使梁上翼缘受力过于集中造成部分混凝土脱落.

图1　健康梁PC-1,PC-2和翼缘损伤梁PC-3

梁的截面几何尺寸以及截面配筋如图2所示,构件的设计要求参照《混凝土结构设计规范》[13].

图2　试验构件截面尺寸及配筋图

实验室采用后张法制作预应力混凝土U型梁,浇筑采用的混凝土等级为C40,纵向非预应力钢筋和箍筋均为HPB235级钢筋.试验构件所用各材料经材性试验所得各参数如表1所示(见下页).Ec,E′c分别为混凝土和预应力钢筋线的弹性模量实测值,fcu为混凝土立方体轴心抗压强度实测值,fpt为钢绞线极限强度实测值.另外,纵向非预应力钢筋屈服强度实测值fyv为262 MPa,箍筋屈服强度实测值fyv为256 MPa.

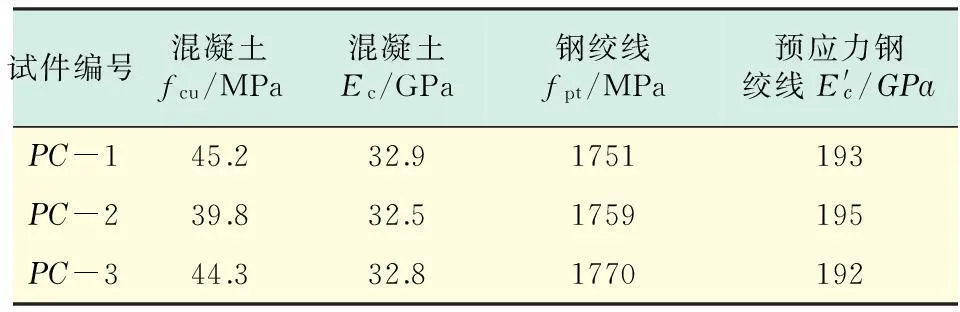
表1　试验构件材料参数表

3.2动力测试方案

试验研究的内容:

a. 采样频率对U形梁模态分析结果精度的影响;

b. 翼缘损伤对U形梁固有频率的影响;

c. 不同外部荷载激励对U形梁固有频率的影响.

为了采集到相应的数据,应确保试验环境处于相对安静稳定的状态之下,以减少噪声影响.然后,通过软件实时测试窗口,确保仪器正常稳定工作后开始数据采集,采集的有效数据记录长度设置为30 s,采样频率分别设置为512,1 024 Hz.采集的梁状态分为空载、静载和动载这3种.其中,静载模拟一个体重70 kg的人在梁中点处静止站立;动载采用人激振动加载法,即一个体重约70 kg的人使其质量中心作频率为1 Hz、双振幅为15 cm的前后摆臂运动时,将产生大约0.2 kN的惯性力.采集过程中需要监控通道中信号的波形情况及变化,对于不符合要求的信号及时予以停止,经检查合格后再进行采集[14].

3.3测点布设

试验采集系统用到的装置有IEPE低阻抗电压输出通用型传感器、INV306A型信号采集分析仪、DASP-V10多通道信号采集和实时分析软件.

为了以尽可能少的传感器测点数来获取最可靠、最全面的结构振动信息[15],试验选取梁支座间距的二分点、三分点、四分点以及一端支座处共6个待测点,分别采集梁竖向和横向的加速度响应,测点的位置如图3所示.

图3　测点布置示意图

4预应力混凝土U形梁模态参数识别

试验得到各测点加速度时程曲线后,需要先对采集信号进行滤波处理,根据文献[16],同时考虑到U形梁中预应力钢绞线对梁体的轴向压力将导致梁体的整体刚度下降，从而引起梁体的自振频率下降的情况,将噪声频率范围定为0～80 Hz以及大于600 Hz的部分.

4.1健康梁的模态参数识别

4.1.1试验数据采集与模态参数识别

空载情况下,对试件PC-1进行采样频率为1 024 Hz的数据采样,如图4所示.a为加速度，t为时间.通过NExT技术,选取测点1和测点2两组信号计算互相关函数.因为,测点1位于梁支座处,受环境噪声影响较小,可作为计算互相关函数的参照点数据;测点2信号作为响应点数据.

图4　梁PC-1测点1～6全程信号

选择好数据后,经S变换,将两组信号中每一个采样点的瞬时能量值在时频域中展开,再经S变换滤波,结果如图5所示.

再将两组处理后的信号进行互相关函数分析,得到互相关函数f如图6所示.

将得到的结果作为U形梁结构的激励,通过Matlab编程实现NExT-ITD法,计算出U形梁的模态参数(即频率),计算结果如图7所示.

从图7可以看出,经S变换去噪后,其一阶和三阶频率较去噪前有所减小,说明滤波能够减小噪声对原信号的影响,这将有利于结构的模态参数识别.

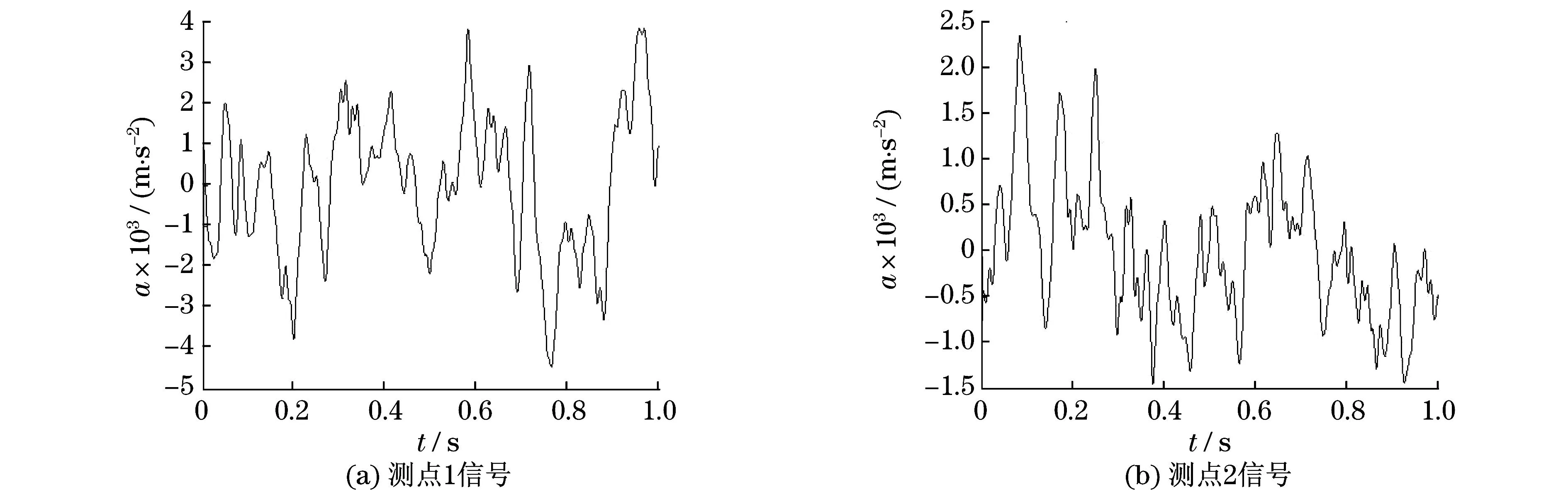
图5　去噪后信号

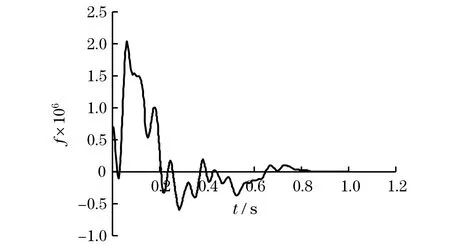
图6　信号的互相关函数

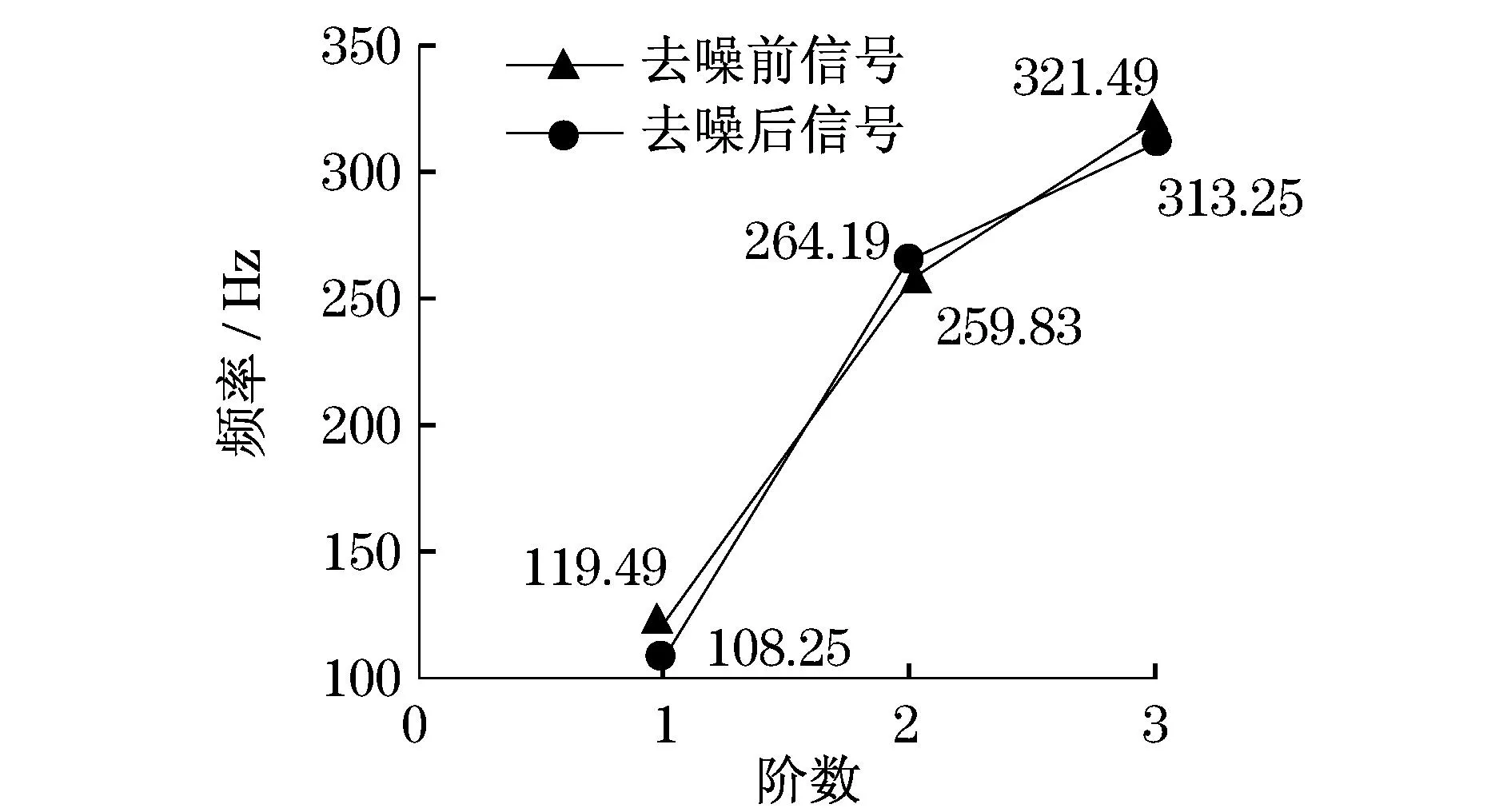
图7　去噪前和去噪后信号识别结果对比

同理,计算采样频率为512 Hz时U形梁的模态参数,计算结果如表2所示.

表2 U形梁动力测试结果

Tab.2Dynamic test results of U-shaped beam

采样频率/Hz一阶频率/Hz二阶频率/Hz三阶频率/Hz51298.60254.34302.161024108.25264.19313.25

由表2可以看出,采样频率为512 Hz的计算结果均小于采样频率为1 024 Hz相应阶数的计算结果.根据采样定理[17]:当采样频率fs低于分析信号的最高频率fmax的两倍时,就会引起“频率混淆”现象,从而造成信号的失真.因此,对于信号的时域分析,采样频率越高,则数据的采样结果与原信号就越接近,误差也越小.

4.1.2ANSYS有限元分析的模态验证

选用Link8单元模拟钢筋,Solid65单元模拟混凝土,建立分离式模型.离散模型的钢筋单元与混凝土单元共用节点,以实现整体工作过程中自由度的耦合.运用ANSYS对U形梁进行模态分析，确定梁的固有频率和振型,并取其前三阶振型,如图8所示(见下页),对应的前三阶频率ωi(i=1,2,3)分别为105.78,276.26,305.57 Hz.

根据有限元模态分析所得结果与试验所得频率数据相比较,采样频率为512 Hz时,前三阶频率误差分别为6.8%,7.9%,1.1%,采样频率为1 024 Hz时,误差为2.3%,4.3%,2.5%.

由此可以说明,试验分析所得频率数据是合理的同时,也定性地反映出当采样频率为1 024 Hz时,采样数据的识别精度更高,此时的动测结果与ANSYS的计算模态分析结果更相近,频率误差率都在5%以内.

4.2翼缘受损梁的模态参数识别

空载情况下,对试件PC-3进行采样频率为1 024 Hz的数据采样,采集数据如图9所示(见下页).

根据采样信号,选择测点1和测点4信号数据进行S变换滤波处理,再用NExT-ITD法进行分析,结果如图10所示(见下页).

对比图10所示各工况频率数据,一阶、二阶、三阶频率的变化率分别为2.8%，1.5%，6.1%.翼缘受损梁的第三阶模态频率远大于健康梁的第三阶模态频率.因此,可以认为,三阶频率在U形梁翼缘受损时比较敏感,可以作为判断U形梁翼缘受损的一项识别指标.

图8　U形梁前三阶模态

图9　梁PC-3测点1～6全程信号

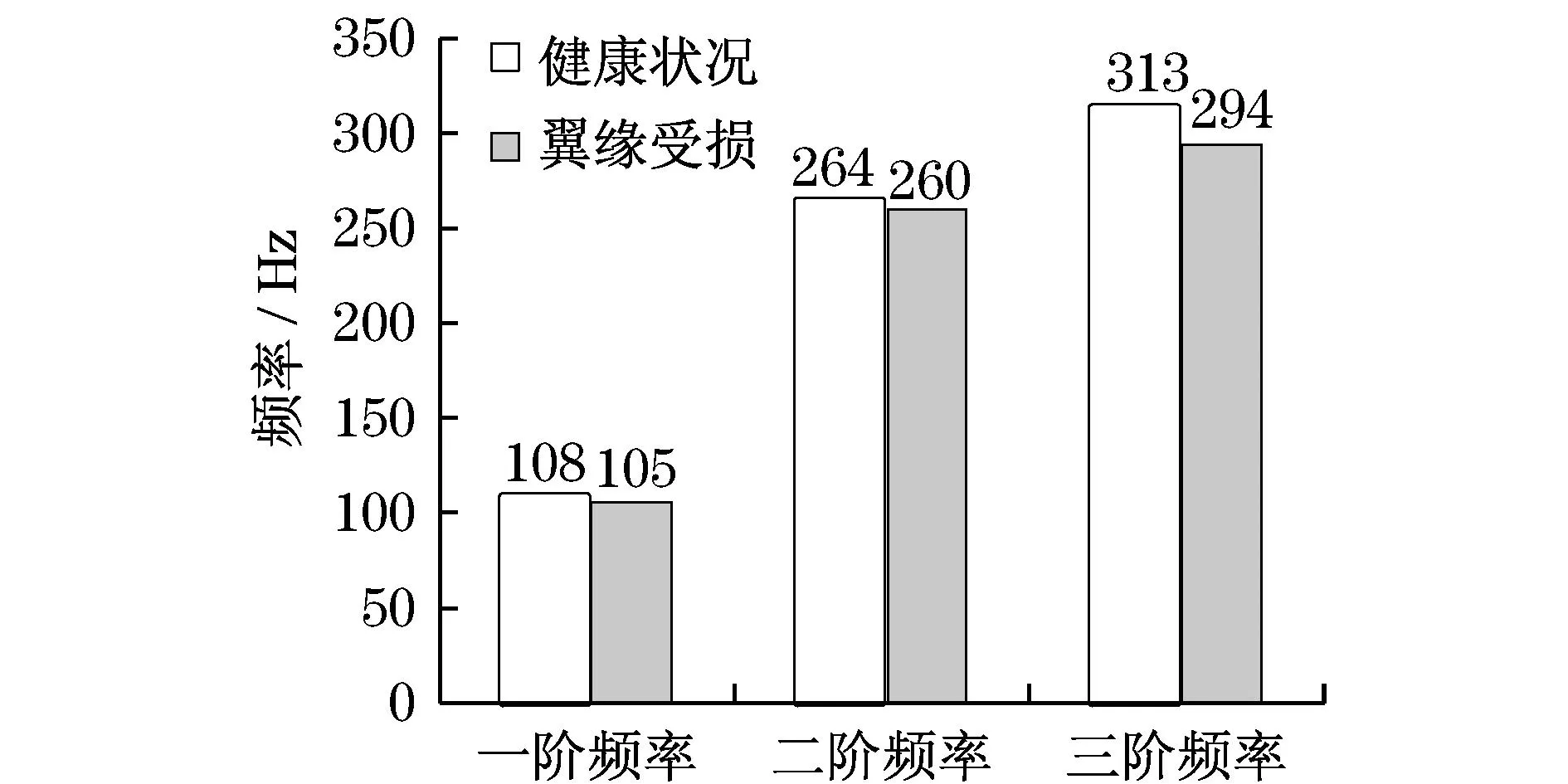
图10　健康梁与受损梁前三阶频率对比

4.3静载状况下健康梁的模态参数识别

试件PC-1在静载作用时,进行采样频率为1 024 Hz的数据采样,试验采集数据如图11所示.

以测点1和测点3的信号为分析对象,计算结果如12所示.

图11　梁PC-1静载时测点1～6的全程信号

图12　无载与静载健康梁前三阶频率对比

由图12,静载状态下,U形梁的前三阶频率与无载状态下的U形梁相比,一阶频率折减1.9%,二阶频率增加3.0%,三阶频率增加5.1%.

根据固有频率公式

(3)

并结合本试验结果可看出，梁上静止人的试验表明,人体不能等同于一重物,简单地视为一个惯性质量模型加以考虑,而应视为一个质量-弹簧-阻尼系统,与梁构成一个组合系统进行分析.

4.4动载状况下健康梁的模态参数识别

对于动载情况,同样对试件PC-1进行试验,对采样数据通过S变换进行滤波处理,再用NExT-ITD法进行分析,所得结果如图13所示.

图13　3种荷载状态下健康梁前三阶频率对比

由图13中的数据对比可知,动载所得模态频率高于无载和静载所得模态频率,说明对于站立人体以摆臂作为外部激励时,人体对于振动结构不能以惯性质量来描述;同样地，站立的人体以摆臂激励梁体时也不等同于人在梁上行走或跳跃的情况[18],不能将其视为一简单的移动荷载,而应视为一个质量-弹簧-阻尼系统,与U形梁一并视为一个多自由度耦合系统进行动力分析.

5结论

通过对3根1∶10缩尺预应力混凝土U形梁的动力测试,采用基于S变换的滤波技术和NExT-ITD法采集信号进行了模态参数识别,结论如下:

a. 当采样频率为1 024 Hz时,与512 Hz相比,数据的采样结果与原信号越接近,误差越小,模态分析的结果精度越高.

b. 翼缘受损梁与健康梁相比,其前两阶模态频率基本没有变化,第三阶模态频率变化较其他两阶大.因此,将第三阶频率作为判断U形梁翼缘受损的一项识别指标是合理的.

c. 静载状况下U形梁的前三阶频率与无载状态下相比,有一定的折减,前三阶频率虽都有所减小,但前两阶频率的折减系数较大,二阶频率折减系数最大.

d. 站立人体摆臂作为外部动载激励时,人不应视为一个惯性质量,而是一个质量-弹簧-阻尼系统,与U形梁一起作为一个多自由度耦合系统进行动力分析,且所得模态频率高于无载时所得到的模态频率.

参考文献：

[1]胥为捷,薛伟辰.预应力混凝土槽形梁的研究与应用[J].建筑结构,2006,36(S):100-105.

[2]谢炯.上海轨道交通高架桥U形梁的技术特点[J].城市轨道交通研究,2012(3):53-57.

[3]曹明旭.预应力混凝土槽形梁的应用现状与前景[J].现代交通技,2009,6(2):30-33.

[4]James III G H,Carne T G,Lauffer J P.The natural excitation technique(NExT)for modal parameter extraction from operating wind turbines[R].California:Sandia National Laboratories,1993.

[5]Caicedo J M,Dyke S J,Johnson E A.Natural excitation technique and eigensystem realization algorithm for phase I of the IASC-ASCE Benchmark problem:simulated data[J].Journal of Engineering Mechanics,2004,130(1):49-60.

[6]王济,胡晓.Matlab在振动信号处理中的应用[M].北京:中国水利水电出版社,2006.

[7]Ibrahim S R.Double least squares approach for use in structural modal identification[J].AIAA Journal,1986,24(3):409-503.

[8]王成瑞.ITD法辨别模态参数的有效性研究[J].机械设计,1995(9):5-7.

[9]罗奎.基于自然激励技术的结构模态参数识别应用研究[D].武汉:武汉理工大学,2010.

[10]程娇.基于小波变换和独立分量分析的去噪方法研究[D].上海:复旦大学,2010.

[11]赵淑红,朱光明.S变换时频滤波去噪方法[J].石油地球物理勘探,2007,42(4):402-406.

[12]Pinnegar C R,Mansinha L.The S-transform with windows of arbitrary and varying shape[J].Geophysics,2003,68(1):381-385.

[13]赵基达,徐有邻,黄小坤,等.GB50010-2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.

[14]郭耀.基于动力特性的简支U形梁损伤识别[D].上海:上海理工大学,2014.

[15]周奎,宁娜娜,林杰.基于频率响应的悬臂工字型钢梁的结构损伤分析[J].上海理工大学学报,2014,36(5):497-501.

[16]赵亚平.钢筋混凝土梁损伤诊断的振动模态分析方法[D].北京:中国农业大学,2005.

[17]贺岷珏,郑小亮.不同采样频率下的伪码同步性能分析[J].中国新通信,2014(1):81-83.

[18]季天健,Bell A.感知结构概念[M].武岳,孙晓颖,李强,译.北京:高等教育出版社,2009.

(编辑:石瑛)

Modal Identification of Simply Supported U-Shaped Beam Based on Dynamic Characteristics Tests

ZHOU Kui,MIAO Runhan,GUO Yao,LIU Yi

(School of Environment and Architecture,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：Dynamic tests on three pre-stressed reinforced concrete U-shaped beams,with the scale of 1∶10,were carried out by using ambient excitation technique and filtering technique based on S-transform,by virtue of the basic theory of natural excitation technique (NExT) and ibrahim time domain technique (ITD).The modal parameters extracted from the tests results were used to analyze the influences of different sampling frequencies,flange damage of main girder web and different load excitation on the dynamic characteristics of U-shaped beams.

Keywords：U-shaped beam; ambient excitation; S-transform; modal identification

中图分类号：TU 391

文献标志码：A

收稿日期：2015-06-23

DOI：10.13255/j.cnki.jusst.2016.02.017

文章编号：1007-6735(2016)02-0192-06

第一作者： 周奎(1970-),男,副教授.研究方向:工程结构抗震、结构健康监测与损伤识别.E-mail:zhoukui_sh@163.com