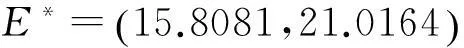具有Hassell-Varley型反应函数的捕食者-食饵系统的随机建模
2016-06-02许超群原三领
费 清, 许超群, 原三领
(上海理工大学 理学院,上海 200093)
具有Hassell-Varley型反应函数的捕食者-食饵系统的随机建模
费清,许超群,原三领
(上海理工大学 理学院,上海200093)
摘要:基于具有Hassell-Varley型功能反应函数的确定性捕食系统建立了两类新的随机捕食者-食饵模型:连续时间马尔科夫链模型和伊藤型随机微分方程模型.分析了不同形式的出生率和死亡率对模型动力学的影响,并通过数值模拟讨论了模型的渐近性态.
关键词:捕食者-食饵模型; Hassell-Varley型反应函数; 连续时间马尔科夫链; 随机建模
1问题的提出
在种群动力学中,捕食者-食饵模型一直是研究者重点关注、研究最多的模型.一般的捕食者-食饵模型具有如下结构[1]:
(1)
式中:x与y分别为食饵和捕食者的数量;r为食饵种群的内禀增长率;K为环境最大容纳量;ε为食饵转化为捕食者的转化率;μ为捕食者的死亡率;g(x,y)为捕食者对食饵的功能性反应函数.
在模型(1)中,捕食者对食饵的功能反应函数g(x,y)起着重要的作用.陈兰荪等[1]总结了g(x,y)常见的几种形式,例如,Holling I-III型[2]、Beddington-DeAngelis型[3]、Crowley-Martin型[4]、比率依赖型[5]等.根据具体的生物背景,研究者们选取不同的功能反应函数建立了不同的模型[6-7].例如,张拥军等[6]建立了捕食者具有传染病且功能性反应函数为仅依赖被捕食者的捕食模型,通过构造Liapunov函数得到平衡点的局部稳定性和全局渐近稳定性的充分条件;孙凯玲等[7]研究了捕食者具有性别偏食且功能反应函数为Holling III型的捕食模型,通过构造Liapunov函数证明了系统周期解的存在唯一性,讨论了周期解全局稳定性的充分条件.
最近,Hsu等[8]研究了如下具有Hassell-Varley(HV)型功能反应函数的捕食模型:
(2)
式中:e为单位时间内捕食者与所有食饵相遇的概率;c为每次相遇捕食成功的概率;h为捕食者与食饵搏斗的时间;α为HV常量,α∈[0,1].
在文献[8]中,给出了平衡点局部稳定的条件,讨论了系统的一致持久性,证明了当α=1/2时,系统存在唯一极限环.Wang[9]考虑了一类具有Hassell-Varley型功能反应函数的时滞捕食者-食饵模型的周期解,利用正重合度定理得到了正周期解存在的充分条件.
上述研究均忽略了环境波动对捕食系统的影响,然而,种群所处的环境会受到各种随机因素(如气候、温度等)的影响[10-11],而这些因素可能会对模型的动力学产生很大的影响.因此,本文以模型(2)为基础,建立了两类具有Hassell-Varley型功能反应函数的随机捕食者-食饵模型:一类是连续时间马尔科夫链模型,另一类是伊藤型随机微分方程模型.其中,随机微分方程模型的建立是以前者为基础,并通过数值模拟讨论模型的渐近性态.
2连续时间马尔科夫链模型的建立
基于常微分模型(2)建立其相应的连续时间马尔科夫链模型.设X(t)和Y(t)为离散随机变量,分别表示t时刻食饵与捕食者数量,其中,X(t),Y(t)∈{0,1,2,…,N},t∈+.在从t时刻变化到t+Δt时刻时,随机变量X(t)和Y(t)的变化为ΔX和ΔY,其中,ΔX=X(t+Δt)-X(t),ΔY=Y(t+Δt)-Y(t),且Δt是充分小的时间段,使得,即在充分短的时间内,至少存在出生或者死亡,且出生和死亡仅发生一次.给定初值X(0)=x0>0,Y(0)=y0>0,则二元随机过程{(X(t),Y(t))}的联合概率函数为
现分别用随机变量X(t)和Y(t)的生灭过程来建立连续时间马尔科夫链模型.设ai和bi(i=1,2)分别为食饵和捕食者的出生率和死亡率,其中
(3)
则其无穷小转移概率为[12]

(4)
概率px,y满足柯尔莫哥向前方程
当y=0时,有
当x=0,又有
且
两个变量过程的分布阶数可以由柯尔莫哥向前方程推导出,于是,矩母函数是有如下形式:
其中,θ1,θ2∈.
其中,(ε1,ε2)∈(0,x)×(0,y),δ∈(ε1,x),η∈(ε2,y),可以得出矩母函数是如下偏微分方程的一个解:
上式两端同时对θ1求偏导,可以得到
令上式中θ1=θ2=0,可以得出x期望满足的微分方程为
又由于
同理,可以得到y期望满足的微分方程为
类似的方法得出n阶矩所满足的微分方程为
可以直观地看出x的均值被最大环境容纳量所约束,由x∈{0,1,2,…},x的期望是非负的,满足不等式
进而有
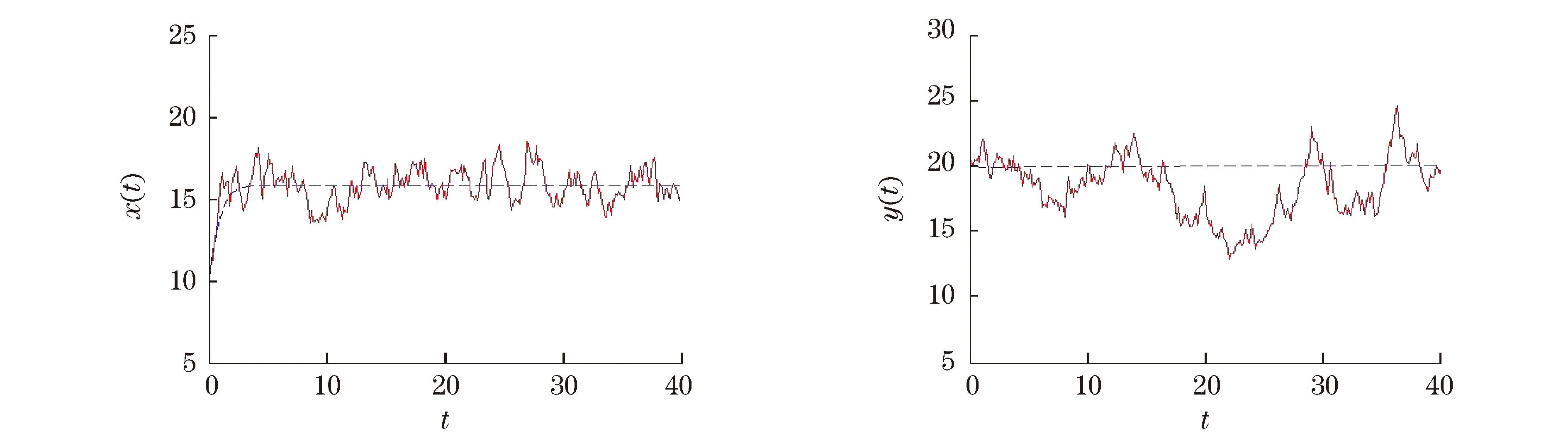
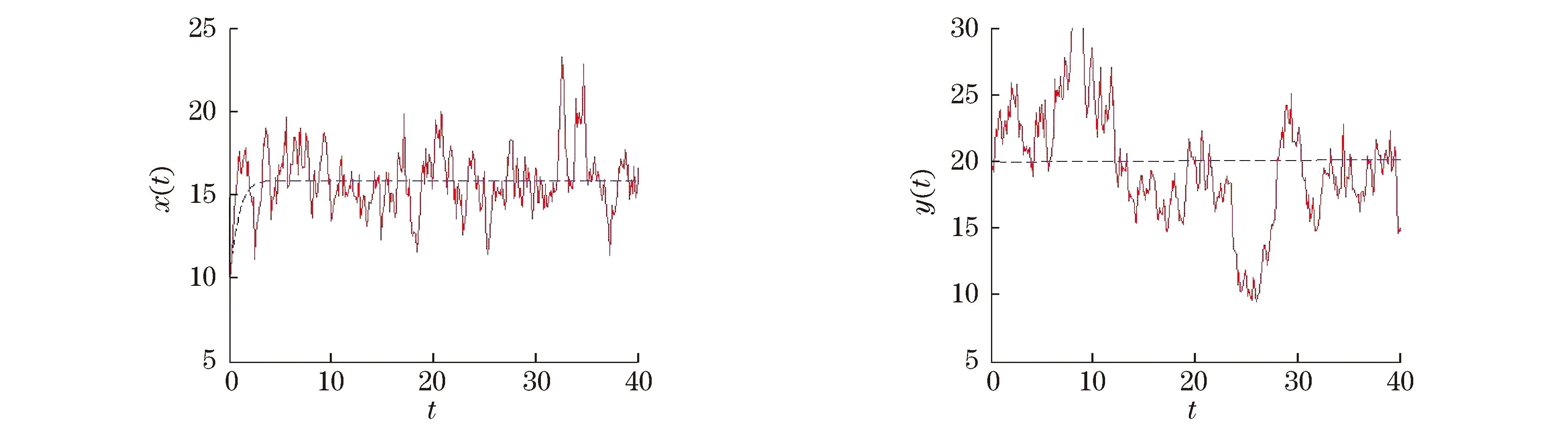
若0 3伊藤型随机微分方程的推导 现以确定性模型(2)为基础,利用上述马尔科夫链模型等[12]建立相应的伊藤型随机微分方程. 充分小时间Δt内Δx与Δy的方差分别为 Δx与Δy的协方差为 因此,ΔZ的协方差为 又因为 所以,Var(ΔZ)≈M2Δt. (5) 由文献[12]可知,方程(5)是伊藤型随机微分方程的一个欧拉近似,即式(5)收敛到如下伊藤型随机微分方程: dZ=μdt+MdB (6) 式中:B=(B1,B2)T,B1和B2分别表示相互独立的标准布朗运动;μ为漂移系数;M为扩散矩阵. 注意到μ与M的表达式,方程(6)即为 (7) 由文献[13]可知,方程(6)的形式可以不唯一,且与之等价的随机微分方程具有相同的联合概率密度函数.与方程(6)等价的随机微分方程具有如下形式: dZ=μdt+CdB* 其中,扩散矩阵C满足CCT=M2.例如, 上述假设出生率和死亡率分别为模型(2)的正项和负项部分,得到了伊藤型随机微分方程(7).当出生率和死亡率取其他形式时,可以得到与方程(7)不同形式的伊藤型随机微分方程. 例如,选取 其中,aij,bij>0,i,j=1,2,且满足以下关系 (8) 对于重新定义的ai和bi,通过类似方法可以得到如下的伊藤型随机微分方程: (9) 由ai1+bi1>αi,ai2+bi2>βi可知,方程(9)中的扩散系数比方程(7)中的扩散系数大. 4仿真与讨论 基于具有Hassell-Varley型功能反应函数的确定性捕食系统建立了两类新的随机捕食者-食饵模型:一类是连续时间马尔科夫链模型;另一类是伊藤型随机微分方程模型.分析了不同形式的出生率和死亡率对随机模型的影响.现通过数值模拟讨论模型的渐近性态. 图1 确定性模型(2)和随机模型(7)的解曲线 从图1和图2察到随机模型(7)和随机模型(9)的解都围绕确定模型(2)的正平衡点E*振荡.比较图1和图2可以发现,随机模型(9)解的振荡幅度明显大于随机模型(7)解的振荡幅度,这与理论结果相符. 图3(见下页)是马尔科夫链模型(4)的二维随机游走,容易看出,马尔科夫链模型(4)的随机游走是围绕确定性模型(2)的正平衡点E*进行的. 图2 确定性模型(2)和随机模型(9)的解曲线 图3 马尔科夫链模型(4)的随机游走 参考文献: [1]陈兰荪,宋新宇,陆征一.数学生态学模型与研究方法[M].成都:四川科学技术出版社,2003. [2]Walley G S.The Odonata of Canada and Alaska[J].The Canadian Entomologist,1959,91(5):291-292. [3]Beddington J R.Mutual interference between parasites or predators and its effect on searching efficiency[J].Journal of Animal Ecology,1975,44(1):331-340. [4]Crowley P H,Martin E K.Functional responses and interference within and between year classes of a dragonfly population[J].Journal of the North American Benthological Society,1989,8(3):211-221. [5]Arditi R,Ginzburg L R.Coupling in predator-prey dynamics:ratio dependence[J].Journal of Theoretical Biology,1989,139(3):311-326. [6]张拥军,王美娟,徐金瑞.捕食者具有传染病的捕食系统模型的分析[J].上海理工大学学报,2009,31(5):409-413. [7]孙凯玲,王美娟,朱春娟.具有性别偏食和Holling III类功能反应的食饵捕食者模型[J].上海理工大学学报,2009,31(1):6-10. [8]Hsu S B,Hwang T W,Kuang Y.Global dynamics of a predator-prey model with Hassell-Varley type functional response[J].Discrete and Continuous Dynamical Systems-Series B,2008,10(4):857-871. [9]Wang K.Periodic solutions to a delayed predator-prey model with Hassell-Varley type functional response[J].Nonlinear Analysis:Real World Applications,2011,12(1):137-145. [10]Ji C Y,Jiang D Q,Shi N Z.Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with stochastic perturbation[J].Journal of Mathematical Analysis and Applications,2009,359(2):482-498. [11]Mandal P S,Banerjee M.Stochastic persistence and stationary distribution in a Holling-Tanner type prey-predator model[J].Physica A,2012,391(4):1216-1233. [12]Mandal P S,Allen L J S,Banerjee M.Stochastic modeling of phytoplankton allelopathy[J].Applied Mathematical Modelling,2014,38(5/6):1583-1596. [13]Allen E J,Allen L J S,Arciniega A,et al.Construction of equivalent stochastic differential equation models[J].Stochastic Analysis and Applications,2008,26(2):274-297. (编辑:石瑛) Stochastic Modeling on a Predator-Prey System with Hassell-Varley Type Response Function FEI Qing,XU Chaoqun,YUAN Sanling (College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China) Abstract:Based on a deterministic predator-prey system with Hassell-Varley type response function,two new stochastic predator-prey models,a continuous time Markov chain model and an Ito type stochastic predator-prey model were established.The influences of different forms of birth and death rate on the dynamics of the model were analyzed.Using numerical simulations,the asymptotic behaviors of the models were discussed. Keywords:predator-prey model; Hassell-Varley response function; continuous time Markov chain; stochastic modeling 中图分类号:O 175 文献标志码:A 通信作者:原三领(1966-),男,教授.研究方向:生物数学.E-mail:sanling@usst.edu.cn 基金项目:国家自然科学基金资助项目(11271260);上海市教委科研创新重点项目(13ZZ116);沪江基金资助项目(B14005);上海市一流学科建设资助项目(XTKX2012) 收稿日期:2015-06-23 DOI:10.13255/j.cnki.jusst.2016.02.001 文章编号:1007-6735(2016)02-0103-06 第一作者: 费清(1991-),女,硕士研究生.研究方向:生物数学.E-mail:13075575937@163.com