超声衰减谱法颗粒粒径测量中遗传算法参数优化

汪　雪,　苏明旭,　蔡小舒

(上海理工大学 能源与动力工程学院,上海　200093)



超声衰减谱法颗粒粒径测量中遗传算法参数优化

汪雪,苏明旭,蔡小舒

(上海理工大学 能源与动力工程学院,上海200093)

摘要：在超声衰减谱法测量颗粒粒径分布的反问题求解中,反演算法至关重要,遗传算法作为一种全局最优化算法,其参数优化对于颗粒粒径分布反演效果极其关键.从最大代数、种群尺度、交叉和变异概率等参数优化角度,对于服从3种典型分布函数的颗粒系进行数值模拟.研究发现,当最大代数为300、种群尺度为60、交叉概率范围为0.4～0.85、变异概率为0.045～0.08时,获得的反演结果与设定值较吻合.在此优化参数下的数值算例和对两种玻璃微珠-甘油悬浮液样品的实验超声衰减谱反演,进一步验证了此优化参数下遗传算法具有较好的稳定性和抗噪性.

关键词：超声衰减谱; 颗粒粒径测量; 反演; 遗传算法

近年来随着能源、化工、电子、机械、材料制备、食品、生物医药等与颗粒相关领域的高速发展,颗粒两相流中的颗粒粒径分布获得越来越多的关注.超声衰减谱颗粒粒径测量具有对介质高穿透能力、非浸入式、易实现在线检测、装置简单、成本低等特点,因此在各类方法中具有很强的竞争力[1].超声衰减谱颗粒粒径测量方法的研究主要包括3个方面:超声衰减谱测量技术[2]、超声波理论模型的建立和简化[3]、超声衰减谱反演.其中,反演效果直接关系颗粒粒径分布求解结果的精确度,反演时间也是在线检测实时性的重要考核指标.

典型地,超声衰减谱法测量中反演算法可以分为两类:非独立模式算法与独立模式算法.非独立模式算法通常先假定被测颗粒粒径分布符合某一函数分布(如Rosin-Rammer,即R-R分布,正态(normal/gauss)或对数正态(log normal)分布)[4],然后以理论预测与实测衰减谱的误差作为目标函数来构造最优化问题.对于线性声学模型可不考虑颗粒浓度影响,一般有两个待优化参数.用于颗粒粒径测量的典型非独立模式优化算法包括BFGS (Broyden-Fletcher-Goldfarb-Shanno)[5],DFP(Davidon-Fletcher-Powell)[6]和LM(Levenberg-Marquard)[7]算法等.独立模式算法无需事先设定颗粒系的粒径分布函数,通常利用正则化技术克服方程病态问题后,采用截断奇异值分解(TSVD)等方法直接进行谱的反演得到颗粒系粒径分布.目前研究较多的独立模式算法包括Twomey算法及其改进形式[8-9]、ORT (optimum regularization technique)算法[10]、Chahine算法[11-12].对于不同应用实例,上述反演算法有自己的优势和局限性.就前述非独立模式算法而言,由于属于局部最优算法,在某些情况下其求解不仅仅会偏离真值,甚至产生完全不合理的结果.全局最优化遗传算法同时使用多点搜索信息,具有全局收敛性,并且由于其通用性、鲁棒性强、适合并行计算等特点,在颗粒粒径测量中得到越来越多的关注和应用[13-16].

为此,本文主要研究具有全局最优特征的遗传算法在超声衰减谱法测量颗粒粒径中的参数优化问题.通过算例指出全局最优问题后,针对3种分布函数的多分散颗粒系分析了遗传算法中的4个重要参数:最大遗传代数、种群尺度、交叉概率和变异概率,得出优化参数.之后重点分析遗传算法的噪声抑制,并通过玻璃微珠颗粒实验和图像分析进行对比.

1超声衰减谱反演中的优化问题

在非独立模式超声衰减谱法颗粒粒径测量中,通常先将被测颗粒粒径分布假定为符合某一函数分布(如R-R分布函数、高斯分布或对数正态分布),然后通过理论预测衰减谱与实测值误差来构造一个最小化问题.以R-R分布函数为例,其表达式为

超声衰减谱颗粒粒径测量中的目标函数常采用衰减谱误差函数,式(2)是按理论预测超声衰减谱与实验测量值相对偏差的均方根形式给出的目标函数,即

(2)

式中：asim(fj,φ,R)是理论模型预测超声衰减谱,本文涉及的所有正问题预测均采用ECAH(Epstein-Carhart-Allegra-Hawley)理论模型计算[17-18];ameas,j为实验超声衰减谱(数值模拟中,亦可通过设定粒径计算);f为超声波频率;φ为颗粒相体积百分率;j为超声衰减谱中频率数,j=1,2,…,N.

为验证不同优化算法的适用性,对于设定半径为5 μm的玻璃微珠颗粒进行数值模拟反演计算.按式(2)形式构造目标函数,分别用BFGS,DFP,LM算法和标准遗传算法(standard genetic algorithm,SGA)寻优(粒径区间0～100 μm).对于遗传算法没有设定初始值,另外3种算法设定初始值为50 μm(求解域中值),k0=7.图1(见下页)为4种算法颗粒粒径分布反演结果,从图中可以看出,在该反演算例中,BFGS,DFP和LM这3种局部最优化算法的结果均完全偏离真值,原因在于设定的粒径范围相对真值比较大时,局部最优化方法搜索到局部最优解而结束.与此对应,基本遗传算法结果则基本符合对真值范围的预期,表明发展基于遗传算法的反演技术完全可行.

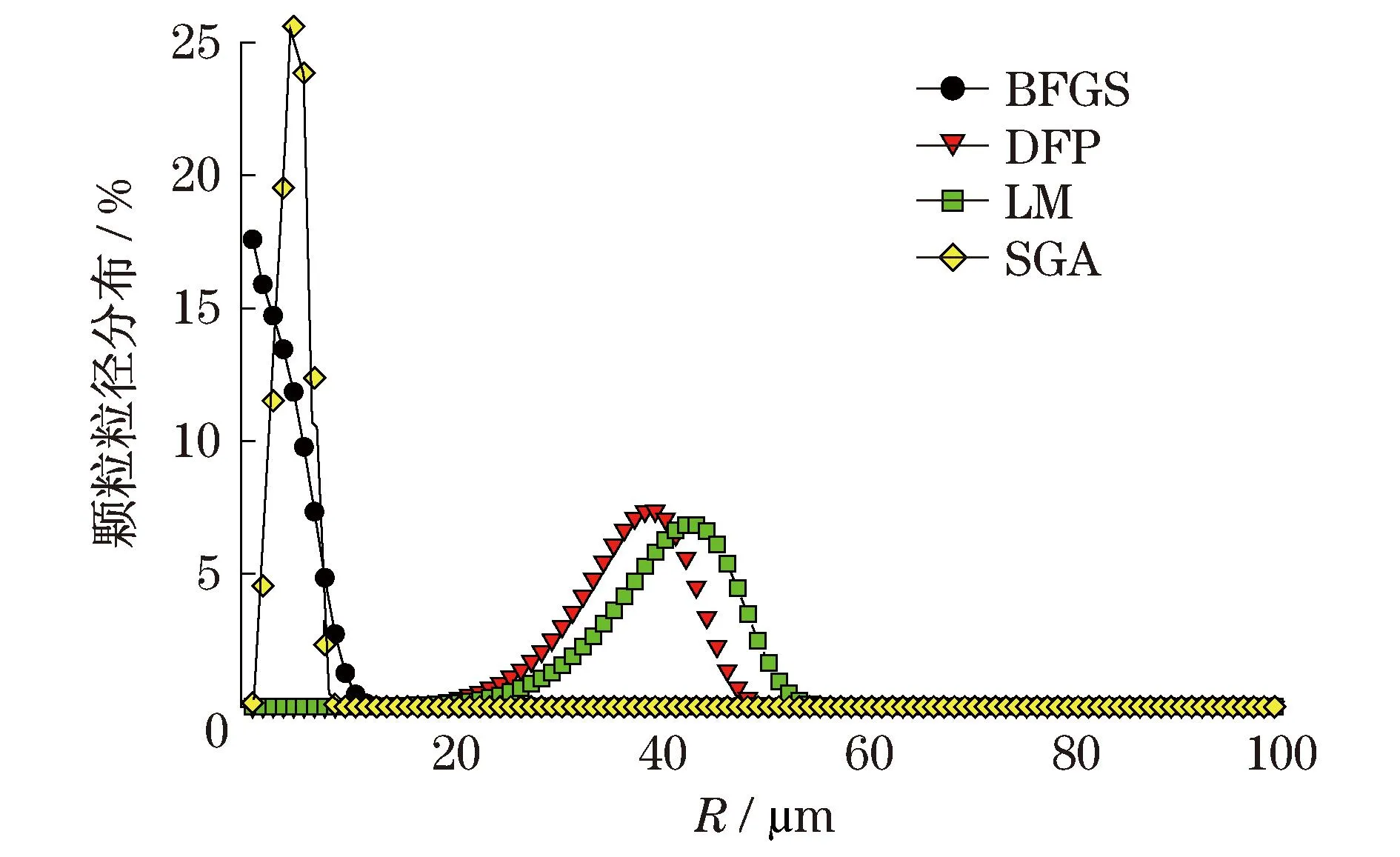
图1　4种算法反演计算的颗粒粒径分布=5 μm)

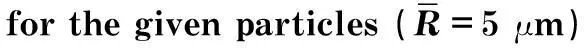
2遗传算法及参数优化

遗传算法是一种基于自然选择和基因遗传学原理的随机并行搜索算法,是一种寻求全局最优解而不需要任何初始化信息的高效优化方法[19-20].但作为一种通用的随机搜索算法,其在一些复杂问题求解中存在早熟收敛和收敛速度慢的缺陷,同时其随机性可能导致计算结果的稳定性和精确度不高.例如,图1中对设定半径5 μm的颗粒,其反演结果为5.72 μm,误差偏大,而且在100次重复模拟中出现16次误差大于50%的情况.因此,需要通过数值方法,以最佳适应度(个体对环境的适应程度)为判据,优化最大代数、种群尺度、交叉概率、变异概率4个重要参数.

2.1最大代数和种群尺度

最大代数是指当产生的代数数目达到该值时,算法停止.该值过高会增加计算量,大大降低算法运行效率;过低则很可能出现未很好收敛即停止的情况,导致结果误差增大,因此需作优化.用遗传算法对目标函数进行500次迭代寻优,其中最佳适应度值和平均适应度值变化如图2所示.在达到约270代后,最佳适应度值已基本稳定,为了保证计算能有效收敛,适当增加迭代次数,选取最大代数为300.

种群尺度指每一代种群的尺寸大小,其选取影响算法的搜索能力和运行效率.较大的种群尺度使得一次进化所覆盖的模式较多,保证群体多样性,从而提高算法的搜索能力,但过多的群体中染色体的个数势必增加算法的计算量,降低算法效率;反之则降低每次进化中群体包含更多较好染色体的能力,易收敛到局部最优解.对3种典型的颗粒粒径分布函数(R-R分布、高斯分布和对数正态分布),分别选取粒径值为5,10,20 μm和多种分布宽度参数为20～110间的10种情形反演.在比较50次平均计算值后,发现种群尺度值大于50以后,最佳适应度值已趋于稳定,选取种群尺度为60.

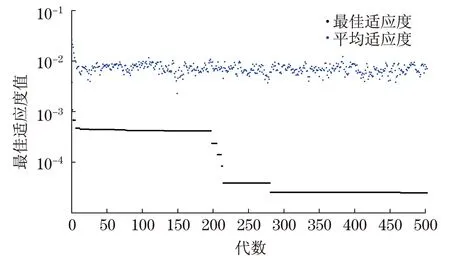
图2　迭代过程中最佳适应度和平均适应度变化趋势

2.2交叉概率和变异概率

交叉指依据交配原则产生一组新解的过程,是产生新个体的主要方法,决定了遗传算法的全局搜索能力.交叉概率决定了进化过程中种群参加交配的染色体平均数目,交叉概率越大,个体产生速度就越快,各代充分交叉.但过大会使群体中的优良模式遭到破坏,优秀个体结构被破坏,从而导致搜索随机化.小的交叉概率有利于减小代沟,保持连续的解空间,但若过小则意味着更多的个体直接复制,搜索过程缓慢甚至陷入停滞状态.通过数值模拟,对不同分布函数在多个平均粒径和分布参数下分别进行0～1间交叉概率寻优.图3为对应的最佳适应度值50次模拟平均结果,显然交叉概率Pc可行范围为[0.4,0.85],本文选0.5.

和交叉不同,变异是编码的某一个分量发生变化的过程.作为产生新个体的辅助方法,它决定了遗传算法的局部搜索能力.变异概率决定了进化过程中群体发生变异的基因平均个数,变异概率大,则增加了群体的多样性.但也可能破坏掉很多好的模式,致使遗传算法变成纯粹的随机搜索,甚至会导致算法由较好的搜索状态倒退.反之,则产生新个体的能力和抑制早熟现象的能力较差,表现为解群体的稳定性好,但一旦陷入局部极值就很难跳出.类似地,对不同分布函数在多个平均粒径和分布参数算例分别进行变异概率Pm为0.000 1～0.1的反演计算,图4给出最佳适应度值50次模拟平均结果,其可行范围为[0.045,0.08],选取0.065.

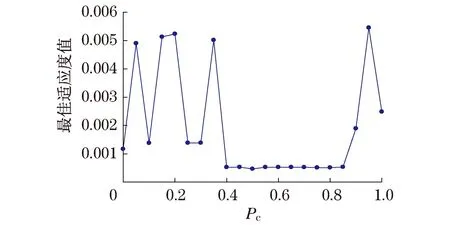
图3　最佳适应度值随交叉概率的变化

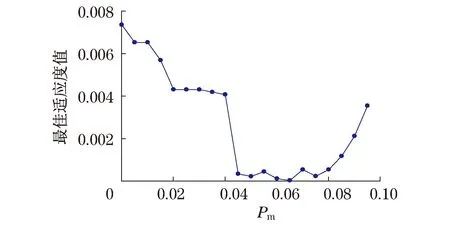
图4　最佳适应度值随变异概率的变化

在初步选取上述参数后,进行参数的交叉校验,发现当改变4个参数中的任意一个,对其余参数优化有一定影响,但取值范围变化不大,对应的最佳适应度值在同一数量级内波动.例如,根据各参数的特性和作用,考虑了交叉概率和变异概率的交叉校验,在种群尺度为60(大于50),最大代数为300(大于270)时,交叉概率取值为0.5或0.6(均在[0.4,0.85]范围内),变异概率可行范围仍为[0.045,0.08],且在0.065处最佳适应度取值最小.综合分析,确定最大代数为300,种群尺度为60,交叉概率为0.5,变异概率为0.065,而经过此参数优化后的方法称为优化遗传算法(improved genetic algorithm,IGA).

3数值模拟

3.1基本和优化算法比较

按照表1参数,对设定(R-R、高斯和对数正态)分布函数,选取不同粒径和分布参数进行数值计算,反演计算取20次平均后得颗粒粒径参数和分布参数.从表中可见,参数优化后分布参数(误差小于5%)明显比基本遗传算法(误差可至20%以上)精确;并且,在100次模拟计算中,均未出现误差大于5%的情况.

表1　3种分布函数下的参数反演结果

3.2抗噪性模拟

由于非独立模式优化算法通常需假定被测颗粒粒径分布符合某一函数,继而通过理论预测衰减谱与实测值误差构造一个最优化问题并确定待定参数.但在实际超声衰减谱的测量过程中,不可避免会产生误差,需要考核算法对于超声谱数据的抗噪性.为此,对给定特征粒径5,10,20 μm的R-R分布颗粒系,在反演前分别在超声衰减谱中加上信噪比(SNR)20 dB至3 dB的高斯白噪声(对应误差均方根为5%～40%),经优化遗传算法反演计算颗粒粒径分布结果,并与设定颗粒粒径分布和无噪声情形对比.

图5(见下页)分别是颗粒粒径为5,10,20 μm，分布宽度k=7的R-R分布颗粒系的反演计算结果曲线.表2(见下页)则给出更多算例下的反演结果数据,表中最大误差为反演值相对设定参数值的误差中最大的那个数值,误差均方根为反演值相对设定参数值的误差的均方根值.可以看出：对于R-R分布函数的颗粒粒径分布,分别对其超声衰减谱加上信噪比20 dB至3 dB的高斯白噪声后,反演粒径参数误差均方根值随着信噪比降低而增大,但都在5%以内;分布宽度k表现出同样趋势,信噪比为20 dB和10 dB时在5%以内,随着信噪比减小至8 dB后,其误差均方根值大于10%,信噪比从8 dB减少至3 dB时，反演分布宽度k误差更大.而在实验室条件下,超声谱测量数据信噪比可以控制在10 dB以上,对于本文实测颗粒的反演计算同样采用R-R分布函数.

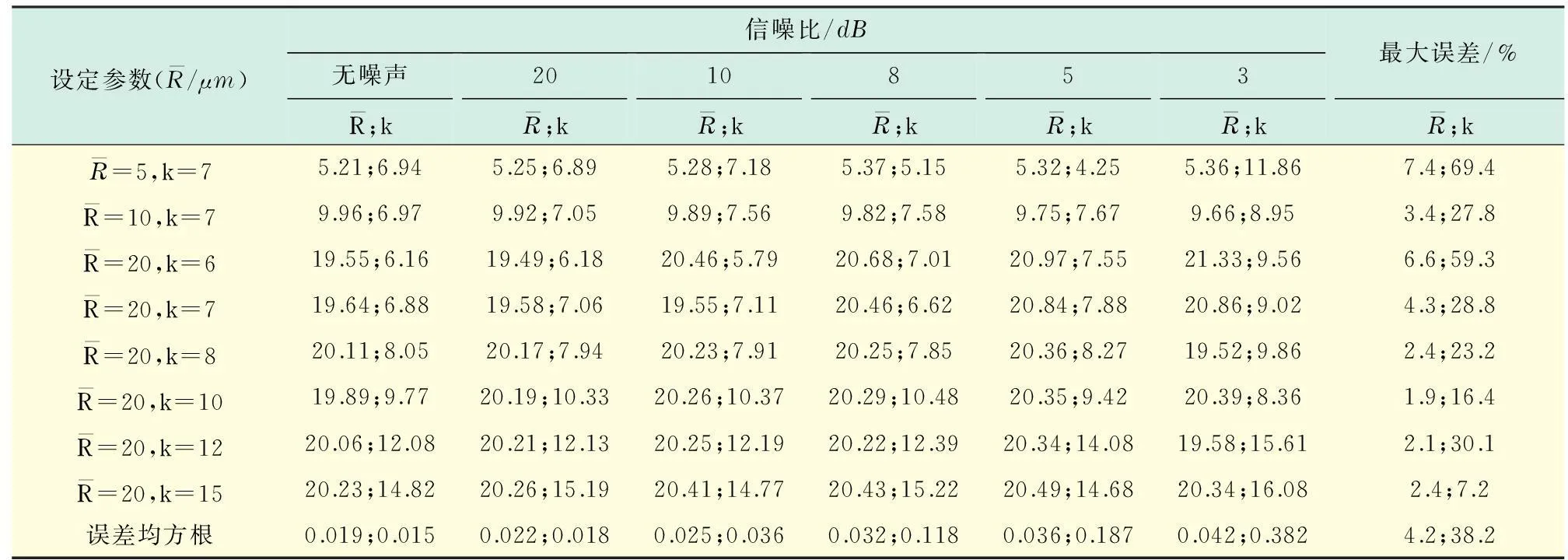
设定参数(R—/μm)信噪比/dB无噪声R—;k20R—;k10R—;k8R—;k5R—;k3R—;k最大误差/%R—;kR—=5,k=75.21;6.945.25;6.895.28;7.185.37;5.155.32;4.255.36;11.867.4;69.4R—=10,k=79.96;6.979.92;7.059.89;7.569.82;7.589.75;7.679.66;8.953.4;27.8R—=20,k=619.55;6.1619.49;6.1820.46;5.7920.68;7.0120.97;7.5521.33;9.566.6;59.3R—=20,k=719.64;6.8819.58;7.0619.55;7.1120.46;6.6220.84;7.8820.86;9.024.3;28.8R—=20,k=820.11;8.0520.17;7.9420.23;7.9120.25;7.8520.36;8.2719.52;9.862.4;23.2R—=20,k=1019.89;9.7720.19;10.3320.26;10.3720.29;10.4820.35;9.4220.39;8.361.9;16.4R—=20,k=1220.06;12.0820.21;12.1320.25;12.1920.22;12.3920.34;14.0819.58;15.612.1;30.1R—=20,k=1520.23;14.8220.26;15.1920.41;14.7720.43;15.2220.49;14.6820.34;16.082.4;7.2误差均方根0.019;0.0150.022;0.0180.025;0.0360.032;0.1180.036;0.1870.042;0.3824.2;38.2

4实测颗粒的反演计算

4.1实验装置和测量方法

实验装置如图6所示,硬件资源主要包括Panametrics 5800PR型超声信号发射接收仪(最高激励频率为35 MHz),一对超声纵波水浸探头M310-SU(标称频率为5 MHz),双通道高速数字化仪(NI公司PCI-5114,最高采样率为250 MS/s,单通道存储容量为8 MB),一个悬浊液恒温测量装置.此外,超声信号采集和处理软件用来获取宽带超声信号,并作频谱分析.

超声衰减谱采用双样法[21]测量:恒温槽中装满水并保持温度约20 ℃,超声波从发射换能器经过恒温槽中水和样品池中的样品后被接收换能器接收,先后使用了厚度为l1(10 mm)和l2(20 mm)的透声样品池,记录下不同厚度样品的透射脉冲波幅度为A1和A2(A1>A2),水的吸收系数为αw,则样品声衰减系数为

(3)

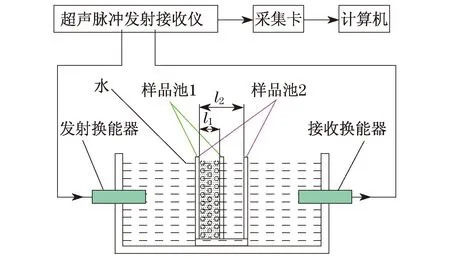
图6　实验系统示意图

4.2两种玻璃微珠颗粒样品的反演计算

实验样品为两种不同粒径分布的玻璃微珠-甘油悬浮液,颗粒密度为4.19 g/cm3,体积分数均为1%,其编号分别为SB040103和SB040107,超声衰减谱法测量前先对样品机械搅拌3 min.图7是显微镜图像法取样分析(MIA)和采用优化遗传算法(IGA)反演的超声衰减谱法颗粒粒径分布(UAS)对比.直方图是采用欧美克公司PIP8.1型颗粒图像处理仪测试结果,中位径Rv50分别为9.62 μm和27.09 μm;样条曲线为超声法结果,中位径Rv50分别为9.51 μm和28.42 μm,该反演结果很好地区分了两种玻璃微珠颗粒样品.此外,样品SB040107的反演粒径分布宽度相对图像法结果的偏差较样品SB040103更大,这主要是因为其粒径更大,颗粒下沉快,影响超声衰减谱的测量,粒径分布宽度反演结果偏差加大.

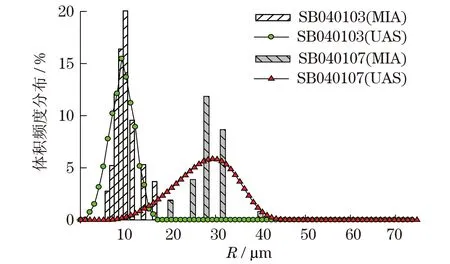
图7　两种方法结果对比

5 结论

对遗传算法在超声衰减谱法测量颗粒粒径分布中的反演计算问题进行了研究.相对于局部最优化方法,遗传算法同时使用多个搜索点的搜索信息,具有全局收敛性,避免了收敛到局部最优解的情况.基于ECAH模型的超声衰减谱法粒径表征反演时,通过对遗传算法参数研究确定的优化参数值分别为:种群尺度为60(大于50),最大代数为300(大于270),交叉概率为0.5(范围为[0.4,0.85]),变异概率为0.065(范围为[0.045,0.08]).由文中数值模拟结果可知,改进遗传算法反演得出的分布参数值(误差小于5%)明显比基本遗传算法(误差达到20%)精确.并且,分别通过数值模拟和对实验测量超声衰减谱的反演验证了改进遗传算法的抗噪性(抗噪能力达到3 dB).同时,有考虑结合局部最优化算法的混合遗传算法,以减少计算代数或者减小种群尺寸,从而提高计算效率,但从目前得到的结果来看还没有获得改善,需要进一步的研究.

参考文献：

[1]Povey M J W.Ultrasound particle sizing:a review[J].Particuology,2013,11(2):135-147.

[2]薛明华,苏明旭,蔡小舒.超声多信号融合表征颗粒两相流实验研究[J].上海理工大学学报,2009,31(1):35-39.

[3]苏明旭,蔡小舒.超细颗粒悬浊液中声衰减和声速的数值模拟——四种模型的比较[J].上海理工大学学报,2002,24(1):21-25.

[4]Allen T.Powder sampling and particle size determination[M].Amsterdam:Elsevier Science,2003.

[5]Babaie-Kafaki S.A modified BFGS algorithm based on a hybrid secant equation[J].Science China Mathematics,2011,54(9):2019-2036.

[6]Zhang L H,Pan P Q,Zhang S P.On the local and superlinear convergence of a parameterized DFP method[J].Numerical Functional Analysis and Optimization,2014,35(1):111-132.

[7]Ding S,Chang X H,Wu Q H.A study on approximation performances of improved BP neural networks based on LM algorithms[J].Applied Mechanics and Materials,2013,411-414:1935-1938.

[8]Igushi T,Yoshida H.Investigation of low-angle laser light scattering patterns using the modified Twomey iterative method for particle sizing[J].Review of Scientific Instruments,2011,82(1):015111.

[9]Zhou J,Moshary F,Gross B,et al.Particle size and refractive index retrieval from the backscattering spectrum of white light using the Twomey iterative method:simulation and experiment[J].Applied Optics,2006,45(26):6876-6885.

[10]Schnablegger H,Glatter O.Optical sizing of small colloidal particles:an optimized regularization technique[J].Applied Optics,1991,30(33):4889-4896.

[11]Liu X Y,Shen J,Thomas J C,et al.Multiangle dynamic light scattering analysis using a modified Chahine method[J].Journal of Quantitative Spectroscopy and Radiative Transfer,2012,113(6):489-497.

[12]Ferri F,Bassini A,Paganini E.Modified version of the Chahine algorithm to invert spectral extinction data for particle sizing[J].Applied Optics,1995,34(25):5829-5839.

[13]Soltanali S,Halladj R,Tayyebi S,et al.Neural network and genetic algorithm for modeling and optimization of effective parameters on synthesized ZSM-5 particle size[J].Materials Letters,2014,136:138-140.

[14]Moradi M H,Abedini M.A combination of genetic algorithm and particle swarm optimization for optimal distributed generation location and sizing in distribution systems with fuzzy optimal theory[J].International Journal of Green Energy,2012,9(7):641-660.

[15]Clementi L A,Vega J R,Gugliotta L M.Particle size distribution of multimodal polymer dispersions by multiangle dynamic light scattering solution of the inverse problem on the basis of a genetic algorithm[J].Particle & Particle Systems Characterization,2012,27(5/6):146-157.

[16]Xu F,Cai X S,Ren K F,et al.Application of genetic algorithm in particle size analysis by multispectral extinction measurements[J].China Particuology,2004,2(6):235-240.

[17]Epstein P S,Carhart R R.The absorption of sound in suspensions and emulsions.I.water fog in air[J].The Journal of the Acoustical Society of America,1953,25(3):553-565.

[18]Allegra J R,Hawley S A.Attenuation of sound in suspensions and emulsions:theory and experiments[J].The Journal of the Acoustical Society of America,1972,51(5):1545-1564.

[19]Saraswat M,Sharma A K.Genetic algorithm for optimization using MATLAB[J].International Journal of Advanced Research in Computer Science,2013,4(3):155-159.

[20]Mohamad N,Ariffin M K A,Ali A,et al.Development of genetic algorithm toolbox using MATLAB in cutting tool path optimization[J].Scientific Research and Essays,2013,8(38):1848-1857.

[21]章维,苏明旭,蔡小舒.基于超声衰减谱和相速度的颗粒粒径测量[J].化工学报,2014,65(3):898-904.

(编辑:丁红艺)

Parameters Optimization of Genetic Inversion Algorithm for Particle Sizing by Ultrasonic Attenuation Spectroscopy

WANG Xue,SU Mingxu,CAI Xiaoshu

(School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：In the inversion problem of particle sizing by ultrasonic attenuation spectroscopy,the inversion algorithm plays an extremely important role.As the genetic algorithm is a global optimization algorithm,it’s highly pivotal to optimize the parameters in genetic algorithm for the inversion effects of particle size distribution.After optimizing the parameters of maximum generation number,population size and genetic operators (crossover fraction and mutation fraction),a series of particle systems with three typical distribution functions were numerically calculated.The numerical simulation reveals that a relatively anastomotic inversion result can be obtained using ultrasonic spectroscopy,as compared to the input particle size distribution,when the maximum generation number is 300,the value of population size is 60 and the ranges for crossover fraction and mutation fraction are 0.4～0.85 and 0.045～0.08 respectively.Finally,the stability and noise immunity of the genetic algorithm based on the optimization of parameters were validated through the numerical and experimental examples of two kinds of micron-sized glass beads-glycerol suspension samples.

Keywords：ultrasound spectroscopy; particle sizing; inversion; genetic algorithm

中图分类号：TB 52

文献标志码：A

通信作者：苏明旭(1973-),男,教授.研究方向:颗粒与两相流测量.E-mail:sumingxu2002@yahoo.com

基金项目：国家自然科学基金资助项目(51176128,51206113)

收稿日期：2015-02-06

DOI：10.13255/j.cnki.jusst.2016.02.009

文章编号：1007-6735(2016)02-0148-06

第一作者： 汪雪(1991-),女,硕士研究生.研究方向:超声颗粒测量.E-mail:enviroment110@163.com