刚-柔支腿对门式起重机挠度的影响*

张大鹏,程文明 ,肖武能

(1.西南交通大学 机械工程研究所,四川 成都　610031；2.绵阳师范学院,四川 绵阳　621000)



刚-柔支腿对门式起重机挠度的影响*

张大鹏1,2†,程文明1,肖武能2

(1.西南交通大学 机械工程研究所,四川 成都610031；2.绵阳师范学院,四川 绵阳621000)

摘要：在工程实际应用中，针对检测砝码重量不足的情况下，评估起重机结构的安全可靠性是检测中急需解决的问题.主梁挠度是起重机整机试验中最重要检测指标，因此，定量地掌握结构参数对主梁挠度的影响尤为重要.对于大跨度大吨位门式起重机，以往的解析计算都没有考虑一刚一柔支腿对主梁挠度的影响.文中针对通用大跨度大吨位门式起重机建立数学模型，在考虑主梁弯矩和支腿弯矩的耦合作用下，基于变分原理求得了门架结构主梁跨中挠度的解析解.然后设计实验模型，在WEW-600B型试验机上进行实验.实验数据表明，门架结构挠度的解析解较原有的计算方法，计算精度有很大提高，为门架结构的设计和检验提供了理论依据.

关键词：门式起重机；挠度；解析解；结构刚度

起重机械是国民经济中重要的基础设备，应用广泛，全国在用的起重机约220万台，其安全问题为人们历来所关注.自2007年铁岭清河特种钢厂发生32人死亡的特大事故后，起重机安全问题受到人们的高度重视.根据《中华人民共和国特种设备安全法》的规定，起重机械在使用前要进行监检(或首检)，使用中也需要定检.起重机在安全检测时，主梁在额载下的挠度是检验的重要项目，以此判断金属结构的安全状态.因此，通过分析起重机结构参数对跨中挠度的影响，获得载荷与挠度的关系具有重要意义.而门式起重机由于支腿参与变形，其挠度的解析式更具有一般性.国内外许多学者对起重机强度和刚度进行了卓有成效的研究与探索.郭建生[1]给出了双刚支腿弯矩对跨中挠度的影响及线性刚度比系数k的取值范围，具有重要意义，但是该文没有考虑支腿不同惯性矩情况，且该文献的算式(1)中的“2k+1”应为“2k+3”.周义清等[2]采用变分原理研究了大挠度梁，求解精度较高，但限于直梁.叶列平等[3]定义了广义结构刚度, 用能量来表达结构构件重要性，具有较高的学术价值,但其未能区分弹性能储存量与构件重要性的关系.陈玉骥等[4]依据势能变分原理论述了大挠度梁内力、位移与荷载的关系，只针对梁结构.

陈长华等[5]基于能量变分原理给出了考虑剪力滞影响的挠度公式，并与传统的挠度公式和初等梁挠度公式进行了比较,分析了剪力滞对箱梁挠度的影响，但仅限于直梁且缺少实验验证.张义民等[6]研究了设计参数的改变对梁结构刚度可靠性的影响, 提出了刚度可靠性灵敏度分析的计算方法，文献[7,8]也通过可靠度指标考量了关键杆件对整体结构的影响，并进行了优化计算，上述文献既有重要的理论价值,也具有重要的工程实际意义.Holst C.等[9,10]通过二元多项式模型来分析主梁挠度，得出主梁挠度主要依赖于载荷大小和位置，结合实验给出了很有意义的门架结构主梁挠度曲线，但没有考虑不同左右支腿惯性矩对挠度的影响，及左右支腿惯性矩不同门架结构会产生侧移的因素.Lee等[11]采用地面激光扫描(TLS)对梁类结构挠度变形进行估算，结合有限元法提出了一种自动计算模型，推断梁结构的应力.但是它很难确定梁的离散化程度，这依赖于结构的边界条件、荷载条件、跨度和变形等等.Castillo E.等[12]通过目标函数分析结构参数的灵敏度，其参考意义局限于桥式起重机.Pinca C. B.等[13]通过有限元对起重机结构承载后的应力应变进行了分析，并给出了参量之间的关系，但是没有考虑加载历程、疲劳程度、制造工艺对计算结果的影响.大跨度大吨位通用门式起重机两侧支腿通常制成一刚一柔，因此，针对大跨度大吨位门式起重机，在考虑主梁弯矩、支腿弯矩的耦合作用下，基于变分原理计算工程中常见的门架结构主梁跨中挠度，对结构挠度的灵敏度进行定性和定量的分析，对门架结构的变形规律进行有益探索，具有重要的工程应用价值.

1主梁下挠度的分析

理论上起重机主梁的下挠度应通过分别计算门架平面和支腿平面内的静挠度相叠加而获得，但由于支腿平面内各构件宽度小，刚度大，变形不大，对总的静挠度贡献很小，故可以忽略不计.因此，只在门架平面内进行分析计算.变截面支腿通常根据辛普生数值积分公式进行折算，求得折算惯性矩.此时门架结构简化为3个梁组成.设主梁CD为梁①，左侧支腿AC为梁②，右侧支腿BD为梁③.梁①跨度为l，梁②和梁③长为h，如图1所示.图中虚线是门架结构变形前的位置.F为作用在跨中点K的集中载荷，梁②和梁③的轴向力为N2，N3；设主梁和左、右侧支腿在门架平面内的惯性矩为Ii(i=1,2,3)，若I2≠I3，则门架结构有水平侧位移，设uK为K点的水平侧移量，vK为K点的下挠值.设M2为梁②在C点对主梁的弯矩，M3为梁③在D点对主梁的弯矩；设g2，g3分别为梁②和梁③的挠曲函数.则对梁②有：

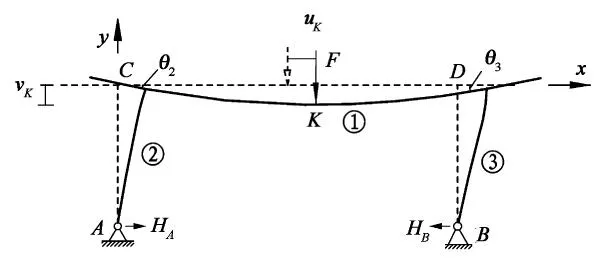
图1　门架结构计算简图

(1)

求解(1)式，得：

(2)

同理，梁③有：

(3)

得梁③的挠曲函数g3为：

(4)

其中，E为弹性模量,I2，I3为左、右侧支腿在门架平面内的惯性矩.

梁②和③在连接点C，D处的转角θC，θD为：

(5)

(6)

设主梁C-K段的挠曲函数为f2，K-D段的挠曲函数为f3，故有：

(7)

将(7)式两边积分，得：

(8)

由变形协调条件，主梁在连接点C，D处的转角θ2，θ3数值上与θC，θD相等，根据主梁所在坐标系(见图1)，θ2取负值，所以有：

(9)

(10)

将(8)式两边积分，得：

f2(x)=

(11)

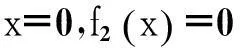
(12)

同理,有：

f3(x)=

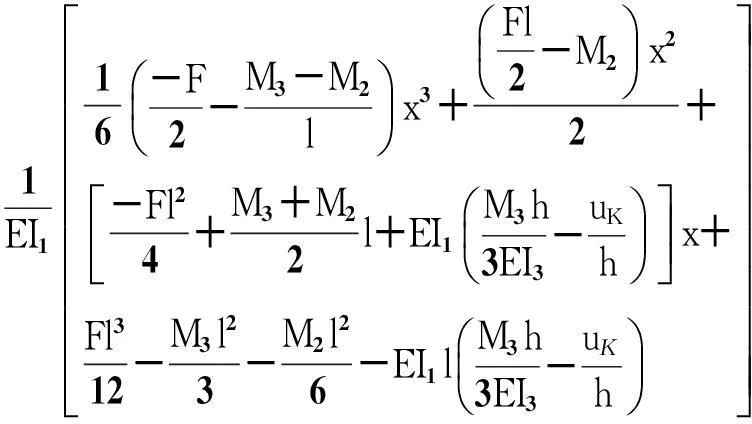
(13)

(14)

(15)

(16)

结构总势能Π等于应变能U与外势能H之和，即：

Π=U+H=

(17)

将边界条件化为(14)和(15)式代入(17)式，并且(17)式应在约束条件(16)式下变分取得驻值.通过引入Lagrange乘子将条件变分问题化为无条件变分问题，得到一个新泛函，并且由这个新泛函一阶变分等于零，得到小变形弹性问题的基本方程和定解条件.现引入Lagrange乘子ζ，并取一阶变分等于零，(17)式变为：

(18)

整理(18)式，得：

(19)

于是由(19)式有：

(20)

(21)

(22)

将(20)， (21)和 (22)式联立求解，整理后再与(14)，(15)式联立，解得：

(23)

(24)

(25)

(26)

2实验

实验在微机控制液压万能实验机WEW-600B型试验机上进行.制作起重机结构模型，安放在试验机上，跨中加载，如图2所示.试件材料为Q235.实验室温度为25 ℃.为减小局部加工痕迹影响，主梁上下表面、支腿侧面采用磨光工艺.采用光栅尺测量试件侧移量，精度为1 μm.加载速率为0.01 kN/s，卸载速率为0.03 kN/s.

实验试件的参数如下：l=350 mm;h=120 mm;I1=43 691 mm4;I2=24 533 mm4;I3=4 393 mm4.实验示意图，见图2，实验按4种工况进行：

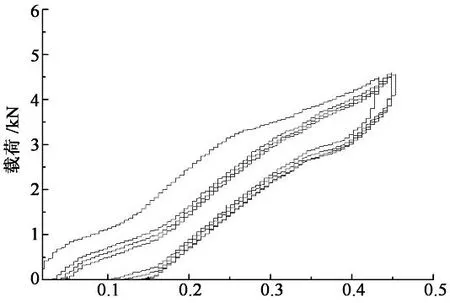
工况1：以相同跨度和相同主梁惯性矩的简支梁进行加载，实验结果如图3(a)；

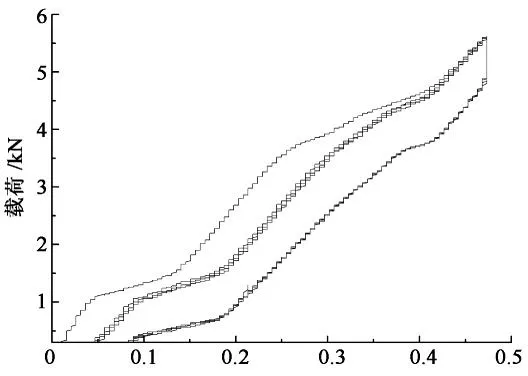
工况2：门架结构底脚不加约束，以静定工况加载，实验结果如图3(b)；

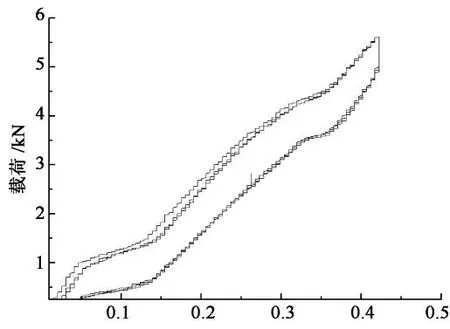
工况3：门架结构两底脚外侧施加约束，此时为一次超静定工况，实验结果如图3(c)；

工况4：门架结构底脚与约束点留有间隙，模拟双缘车轮在大车轨道上的间隙，在滑移到极限时受水平约束力(即轮缘与轨道接触)约束，由门式起重机实际工况按比例缩小,实验中取间隙为0.28 mm，此时为间隙工况，实验结果如图3(d).

1—工作台；2—油缸；3—位移传感器；4—试件；

根据式(23)计算的vK和经典挠度计算公式(27)计算出的挠度值vK′,列于表1.式中符号含义同上.

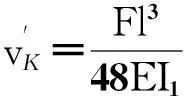
(27)

因为坐标系y轴向上，故所计算挠度值为挠度的相反数，为负值.由计算可知，在相同载荷下按(27)式计算梁挠度大，按(23)的挠度公式计算挠度小.以载荷为4.5 kN为例,(23)式与(27)式相比，两者计算差值0.14 mm.

图3中加载曲线与卸载曲线间的面积为结构耗散能，随着加载循环增加，结构耗散能趋于稳定.图3(c)中随着加载循环次数增加，曲线重合，说明在工况3中，系统对外没有耗散或者耗散非常微小；在工况2,4中，系统对外有耗散，工况2耗散能量大于工况4，因为工况2 底脚有0.55 mm的滑移量，工况4底脚滑移量到0.28 mm时，便受到约束.门架结构总耗散能工况2最大，工况4次之，工况3最小.在载荷加到约4.5kN时挠度曲线出现拐点，继续加载，挠度变化趋于稳定，直至塑性变形.不同载荷下，桥式主梁跨中应力σb与门式主梁跨中应力σg，计算值列于表2.此时试件主梁应力在140 MPa左右.

挠度/mm

挠度/mm

挠度/mm

挠度/mm

MPa

根据门式起重机的工作特点，大跨度时两侧支腿通常制成一刚一柔.由于两侧支腿惯性矩不同，其实际变形必然不同步，其弹性应变能储存也不相同.受结构形式限制，应力在结构中的分布亦不均匀.在加载初期，支腿变形很小，弯曲应变能主要储存在主梁，随着载荷增加，应力逐渐分布到支腿，并趋于均匀.加载初期结构变形不均匀，挠度曲线有波动，在实验中主梁跨中应力达到140 MPa时，结构弹性变形趋于稳定.曲线上端没有屈服迹象，也说明结构处于弹性范围.如果把势能看成广义力，弹性变形能增加率看成广义流，则熵产生趋小.结构挠度增加的过程也就是熵产生减小的过程，也就是结构变形能增加的过程.

在加载起步时，门架结构刚度大，然后减小,后又增加，再减小再增加，在拐点后趋于稳定.因为实验中应力达到140 MPa左右(或载荷加到4.5 kN以后)，各子系统协同度增加，结构趋于稳定.不同工况不同载荷下的挠度见表3.

表3　分级载荷的挠度实验值

实验中，工况3挠度最小，工况4和2挠度依次增加.在载荷为4.5 kN时结构变形稳定,工况3的实验值为0.361 mm.按公式 (27)式和 (23)式计算出的挠度分别为0.446 mm, 0.306 mm,误差率分别为23.8%,15.1%，说明(23)式较原有公式计算精度有很大提高.但是，公式(23)没有考虑主梁剪应力、支腿轴向压缩和二次弯矩的影响，故计算值偏低.

结构承载后不仅产生挠度,而且产生侧移(uK)，主梁水平侧移量与挠度的关系，见图4.图中曲线22,32,42分别是工况2,3,4主梁侧移量与挠度关系的曲线.图中各工况侧移量与挠度均呈非线性.工况2侧移量很小，该工况底脚没有约束，产生滑移,并消耗能量，故侧移量很小，挠度较大.工况3，4底脚有约束，结构侧移储存能量，并且使能量密度趋于均匀，故侧移量较大，挠度较小.工况3，4中,挠度、侧移量和载荷的关系,如图5所示.侧移量与挠度同载荷也是非线性关系.工况3在加载初期结构表现刚度很大,这时刚度是局部接触刚度的体现.实验中为圆柱与弹性半空间接触,其接触刚度c为:

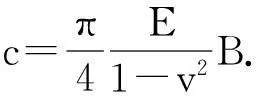
挠度/mm

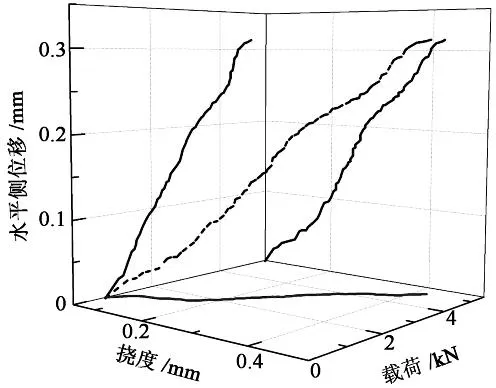
图5　载荷、挠度与侧移量的关系图

工况4与实际情况最吻合，门式起重机大车轮缘比大车轨道宽几十毫米.由于门架结构自重使大车轮与轨道间产生静摩擦力，初始状态为一次超静定工况.当载荷增加到一定数值时，底脚开始滑移，系统对外做功；当滑移使轮缘与轨道侧面间隙消失，底脚再次受到轨道的约束，又变为一次超静定工况.门式起重机工作时是否处于超静定工况，取决于静摩擦力是否大于底脚的水平分力.即：

式中:n为门式起重机自重是额定起重量的倍数；μ为轮轨间摩擦因数；其它符号含义同上文.n取决于门式起重机的结构形式、起升高度、跨度、工作级别等多个因素，通常n取2～7.μ取决于轮轨材料、作业环境等因素，如轨道有无油污，是否室外雨天作业等情况，因此取值范围较大，通常取0.1～0.33.两侧支腿不同，正压力就不同，静摩擦力也就不同，在加载时，一定是一侧底脚先滑移，该轮缘接触钢轨后另一侧又产生滑移，直至两侧底脚都受到约束，变为超静定工况;当然，也可能是交替滑移，当一侧抵触钢轨后，另一侧经过滑移抵触钢轨.同时，挠度-载荷曲线还受门式起重机初始位置的影响，因此挠度必然会产生不确定的波动.门式起重机实际工作情况较实验工况4更复杂，通过测量确定底脚受固定约束前的滑移过程、滑移量及摩擦力是其关键.综上分析，可以按(23)式计算出挠度加上由底脚滑移引起势能减小量所产生的挠度来计算底脚受约束前的挠度；底脚受固定约束后按(23)式计算.

某林场门式起重机采用Wey-50，Wey-100 型电阻应变式位移传感器测量挠度，其分辨能力可达到0.02 mm，实测数据[14]如表4所示，实测跨中载荷与挠度的关系如图6所示.

表4　主梁跨内逐级加载各测点的实测挠度

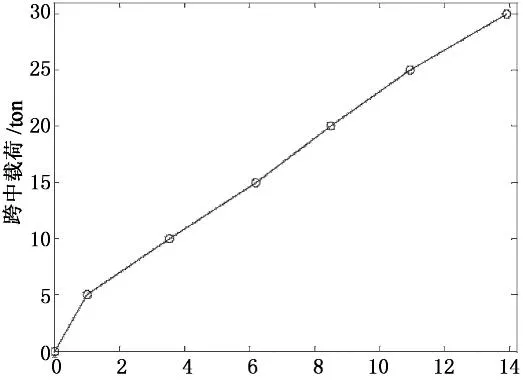
实测跨中挠度/mm

由有限元计算可知实际在用起重机起吊额定载荷时，主梁应力一般在110 MPa以内.实测数据表明，门架结构刚度变化是初始较大，然后减小又增加，而后再减小.与拐点前实验数据变化规律相吻合.说明实验结果较好地反映了门架结构的变形规律，进而验证了本文理论推导的正确性.该门机用原有公式计算的挠度为15.67 mm，实测值为13.90 mm，计算误差为12.73%.实测挠度包含了大车轨道与地基间的间隙和大车轮轴在门架平面竖向的装配间隙，由前面分析可知大车轮轴在主梁纵向上的装配间隙也可引起挠度增大.该门架结构实际挠度要比实测值小，即该门架结构实际刚度要比实测结果好，考虑到上述因素，挠度计算值与实际值的差还会大些.挠度计算值没有考虑支腿对主梁的弯矩，故挠度计算值较大，若采用公式(23)计算，将缩小计算误差.

3结论

通过解析计算与实验可得到以下结论：门架结构处于一次超静定工况时，刚-柔支腿对主梁跨中挠度影响很大，间隙工况次之，静定工况最小.当载荷达到一定值时，载荷-挠度曲线会产生拐点，主梁跨中应力接近140 MPa时，结构趋于稳定.考虑了刚-柔支腿影响的挠度解析解较原有的计算方法，计算精度提高8.7%左右.跨中挠度的解析解对分析结构各参数与挠度的关系也具有重要意义,为门架结构的设计和检验提供了理论依据及有益参考.下一步应考虑主梁剪力、两侧支腿轴向力和弯矩产生的影响.

参考文献

[1]郭建生.集装箱龙门起重机门架结构刚度性能的探讨[J].港口装卸,2001,137(3):11-13.

GUO Jian-sheng. Investigate on the stiffness performance of frame-structure in container gantry crane[J]. Loading and Unloading of Port, 2001, 137(3):11-13.(In Chinese)

[2]周义清,张善元.大挠度梁中的非线性波及其混沌行为[J].中北大学学报:自然科学版,2012,33(6):643-649.

ZHOU Yi-qing, ZHANG Shan-yuan. Solitary waves and chaotic behavior in large-deflection beam[J]. Journal of North University of China: Natural Science Edition, 2012,33(6): 643-649. (In Chinese)

[3]叶列平,林旭川,曲哲,等. 基于广义结构刚度的构件重要性评价方法[J]. 建筑科学与工程学报, 2010,27(1):1-7.

YE Lie-ping, LIN Xu-chuan, QU Zhe,etal. Evaluating method of element importance of structural system based on generalized structural stiffness[J]. Journal of Architecture and Civil Engineering, 2010,27(1):1-7. (In Chinese)

[4]陈玉骥,罗旗帜,刘小洁.变截面薄壁箱形连续梁考虑大挠度和剪力滞影响的力学分析[J].中南大学学报:自然科学版,2008,39(4):845-849.

CHEN Yu-ji, LUO Qi-zhi, LIU Xiao-jie. Mechanics analysis of thin-walled box continuous girder with variable cross-sections in considering influence of large deflection and shear lag[J]. J Cent South Univ: Science and Technology, 2008,39(4): 845-849. (In Chinese)

[5]陈长华,张元海.剪力滞翘曲位移函数对箱形梁挠度的影响[J].兰州交通大学学报,2010,29(4):91-94.

CHEN Chang-hua, ZHANG Yuan-hai. Influence of shear lag warping displacement functions on deflection of box girders[J]. Journal of Lanzhou Jiaotong University, 2010, 29(4): 91-94. (In Chinese)

[6]张义民,贺向东,刘巧伶,等.任意分布参数的梁结构刚度可靠性灵敏度分析[J].计算力学学报,2007,24(6):785-790.

ZHANG Yi-min, HE Xiang-dong, LIU Qiao-ling,etal. Stiffness reliability-based sensitivity analysis of beam structure with arbitrary distribution parameters[J]. Chinese Journal of Computational Mechanics, 2007,24(6): 785-790. (In Chinese)

[7]郑敏,梁枢果,熊铁华.基于可靠度的输电塔抗风优化研究[J].湖南大学学报：自然科学版,2014,41(6):35-42.

ZHENG Min, LIANG Shu-guo, XIONG Tie-hua. Study on the reliability-based wind resistant optimization of transmission line towers[J].Journal of Hunan University: Natural Sciences Edition,2014,41(6):35-42.(In Chinese)

[8]唐和生,苏瑜,薛松涛,等.结构可靠性优化设计的证据理论和微分演化方法[J].湖南大学学报：自然科学版,2014,41(4):33-38.

TANG He-sheng, SU Yu, XUE Song-tao,etal. A Method of reliability design optimization using evidence theory and differential evolution[J]. Journal of Hunan University: Natural Sciences Edition,2014,41(4):33-38.(In Chinese)

[9]HOLST C, BURGHOF M, KUHLMANN H. Modeling the beam deflection of a gantry crane under load[J].Journal of Surveying Engineering，ASCE，2014,140:52-59.

[10]HOLST C, ELING C, KUHLMANN H. Automatic optimization of height network configurations for detection of surface deformations[J]. J Appl Geod, 2013, 7(2): 103-113.

[11]LEE H M, PARK H S. Gage-free stress estimation of a beamlike structure based on terrestrial laser scanning[J]. Comput Aided Civ Infr Eng, 2011, 26(8):647-658.

[12]CASTILLO E, MINGUEZ R, CASTILLO C. Sensitivity analysis in optimization and reliability problems[J]. Reliab Eng Syst Saf, 2008, 93(12):1788-1800.

[13]PINCA C B, TIRIAN G O, JOSAN A,etal. Quantitative and qualitative study on the state of stresses and strains of the strength structure of a crane bridge[J]. WSEAS Trans Appl Theor Mech, 2010,5(4):231-241.

[14]邹云盛,武学文,刘晋浩. 门式起重机桥架静刚度的测定方法[J].森林采运科学，1992(1):38-42.

ZOU Yun-sheng, WU Xue-wen, LIU Jin-hao. Methods on measuring the static stiffness of gantry crane girder[J].Forest Lumbering Science, 1992(1):38-42. (In Chinese)

The Effect of Rigid-soft Legs on Mid-span Deflection in Gantry Cranes

ZHANG Da-peng1,2†， CHENG Wen-ming1,XIAO Wu-neng2

(1.Research Institute of Mechanical Engineering, Southwest Jiaotong Univ, Chengdu,Sichuan610031，China； 2.Mianyang Normal Univ, Mianyang,Sichuan621000， China)

Abstract:In practical application, when the test weight is insufficient, it is urgent to solve the safety and reliability problems of crane structure. The deflection value is one of the key inspection indices of crane girder under rated loading in overall test. Therefore, it is very important that the influence of structure parameters on the mid-span deflection is quantified. For large-span and heavy-duty gantry cranes, the effect of rigid-soft legs on mid-span deflection was not considered in the past. So a mathematical model was established for universal large-span and heavy-duty gantry cranes. Considering the coupling effect of the bending moment of girder and legs, the analytical solution was derived and obtained on the basis of the variational principle. Then, the experimental model was designed and experiments were performed on the WEW-600B type testing machine. The experiment data show that the analytical solution of the gantry-frame structure deflection is more accurate than the pre-existing calculation method, which provides an analytical tool for the design and inspection of gantry structures.

Key words:gantry crane; deflection; analytical solution; structural stiffness

中图分类号：TH213

文献标识码：A

作者简介：张大鹏(1975-)，男，辽宁辽阳人，副教授，博士生 †通讯联系人，E-mail:zdp51368@163.com

基金项目：国家自然科学基金资助项目(51175442)，National Natural Science Foundation of China(51175442) ；国家质量监督检验检疫总局科技计划项目(2010QK02)

收稿日期：2014-11-26

文章编号：1674-2974(2016)04-0009-08