风险偏好的理论与量化——基于金融专业学生的问卷调查

刘晓霞

（湖南工业大学财经学院，湖南株洲412008）



风险偏好的理论与量化
——基于金融专业学生的问卷调查

刘晓霞

（湖南工业大学财经学院，湖南株洲412008）

摘要：本文通过对金融专业学生的风险偏好进行问卷调查，利用前景理论对学生的风险偏好进行了量化研究，让学生更贴切地了解自己的风险态度和理解风险偏好理论，提高其风险意识。

关键词：风险偏好；前景理论；预期效用

金融市场是一个充斥着巨大风险的市场，作为金融行业的后备军，金融专业的学生要着重于风险教育。进行风险教育的前提是学生对风险偏好态度的掌握。本文以金融专业学生为调查对象，通过问卷调查，对学生的风险偏好进行了量化研究，让学生更贴切地理解自己的风险态度和风险偏好理论，提高风险意识。

一、风险偏好的理论

风险偏好是资产选择、资产评估、合约与保险等标准理论中的一个基本概念（Daniel Bernoulli，1738；Kenneth Arrow，1965）。解决风险决策问题的一个著名理论模型是“预期效用理论”。该模型由Von Neumann（1944）和Savage（1954）等人，在继18世纪数学家D.Bernoulli对“圣彼得堡悖论”（St.Petersburg Paradox）的解答基础上并进行严格的公理化阐述而形成的。该模型的基础内涵是，在风险情境下最终结果的效用水平是通过决策主体对各种可能出现结果的加权估价后获得的，决策者谋求的是加权估价后所形成的预期效用的最大化。假设一个人面对一个有两种可能结果的资产：p（0＜p＜1）概率获得财富x，（1-p）的概率获得财富y，那么，预期效用值记作：

这个模型建立在效用U对应着不同财富的假设基础上，通过一些实证调查发现人们的效用函数是凹形的，即是风险规避行为。风险规避者需要得到很大的回报才愿意参与赌博。另外，也存在对风险中性或更偏好风险的人。

为了使预期效用模型能够应用于真实的决策研究，决策制定者一般需要满足四条公理：完整性、传递性、独立性、连续性。然而，一些实验及实证表明，存在着对这些公理的背离。法国经济学家Allais展示了在特定情形下对第三条公理的偏离，这个实验叫做阿莱悖论。

Tversky&Kahneman（1992）提出了著名的前景理论模型，认为人们的风险态度表现为：相对于高概率收益的风险厌恶和相对于高概率损失的风险寻求，相对于低概率收益的风险寻求和相对于低概率损失的风险厌恶。该理论主要用于研究投资者对于收益和损失的风险态度差异，该理论认为个体进行决策实际上是对“期望”的选择。前景理论中“期望”的价值是由“价值函数”和“决策权重”共同决定的，这与期望效用理论中采用的效用函数不同，在该理论中用价值函数v（△x）代替了期望效用理论中的效用函数U（x），用概率权重函数π（p）替代了期望效用理论中的概率p。

价值函数的这几个特点可以用公式表示如下：

其中△x代表了财富的变化，α表示收益部分的风险厌恶，β代表损失部分的风险厌恶，λ表示损失厌恶，见图1。

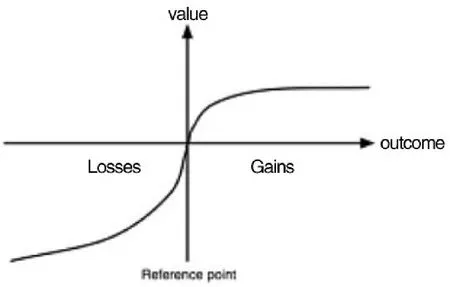
图1　价值函数

Drazen Prelec（1998）对权重函数形式进行了改进，将前景理论表述如下：

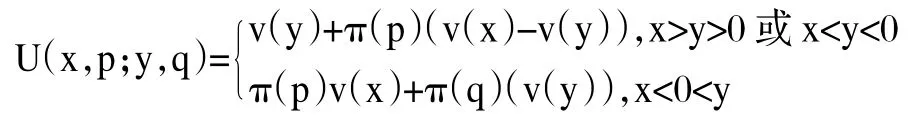
函数表达式中U（x，p；y，q）表示由可能性为p的回报x以及可能性为q的回报y组成的二元期望选择的预期的期望值用v（x）表示价值函数，参数σ和λ分别代表了价值函数的凹性（concavity），以及损失厌恶的程度。π（p）表示权重函数，α表示概率。如果α=1，可能性权重函数是线性的，就和期望效用函数中一样。如果α＜1，权重函数是倒S型的，即个人高估了小概率而低估了大概率。如果α＞1，则权重函数是S型，即个人低估了小概率而高估了大概率事件。当α=1并且λ=1时上述模型等价于期望效用模型。

二、风险偏好的问卷设计与调查

1、问卷设计

该问卷设计借鉴张媛（2010）的问卷，包括两个部分，第一部分是基本信息，包括被调查者的性别、年龄、家庭背景、消费等基本信息。第二部分是风险偏好问题。将被试有关回答分别代入前景理论的公式，可以求出两组σ和α的范围，两组求公共解，即可以得到一个确定的σ和α。另外，因为前景理论的表述中分别考虑了收益或损失两种情形，所以我们设计了问题四引入了损失的情况，通过这个问题的回答与问题二、问题三的结合就可以得到前景理论的另一个参数λ。由于篇幅有限，问卷内容不在此呈现。

2、问卷调查

本次问卷调查针对某省一本和二本学校金融专业的学生，随机发放问卷1000份，回收455份，回收率45.5%。

三、风险偏好的量化

本文使用前述Drazen Prelec（1998）前景理论来描述被试的风险态度。问卷中对于风险偏好的测量是根据我们设计的三个问题得出的。每位被试对于这些问题的回答构成了不等式组，可以根据不等式组求解出前景理论的三个参数值，其中，问题四和问题五的回答决定了σ和α。比如，一个被试在问题四选择答案“1500”（具体问题见附录问卷）。那么根据公式可列不等式组如下：

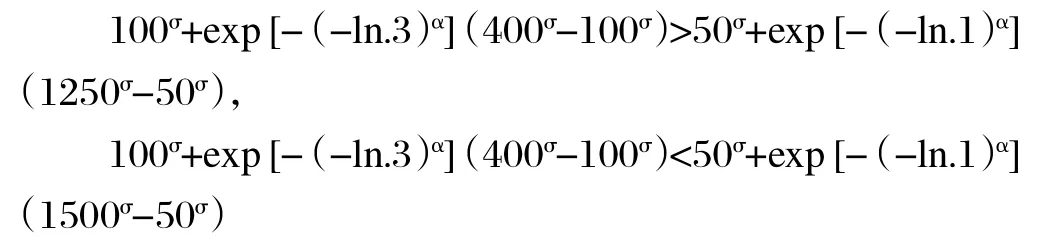
解此不等式组，可得（σ，α）的组合为（0.4，0.4），（0.5，0.5），（0.6，0.6），（0.7，0.7），（0.8，0.8），（0.9，0.9）或（1，1）。假设同一被试在问题五时选择答案“680”，那么满足：

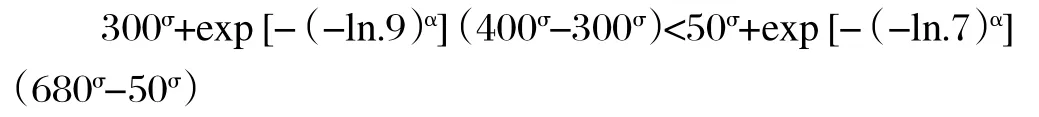
表2　损失厌恶参数λ

解此不等式组可得（σ，α）的组合是（0.8，0.6），（0.7，0.7），（0.6，0.8），（0.5，0.9）或（0.4，1）。通过交叉比较问题四与问题五的答案即可以得到（σ，α）的可能值为（0.7，0.7）。

根据相同方法，可以求出损失厌恶的参数λ，λ由被试对问题四、问题五、问题六的回答共同决定。如被试在问题六时选择答案二，满足不等式组：

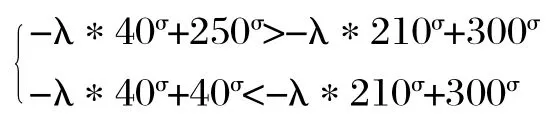
因为根据问题四、问题五已经可以求出σ和α，故将σ代入上述不等式组可以求得λ的范围。

根据上述方法可以求得被试所有可能出现的前景理论参数值，见表1表2。

通过在数据表中编缉命令VLOOKUP，我们可以根据被试对问题四、五、六的回答求出每一个被试的前景理论参数σ、α以及λ的上、下限。

四、结论

本文通过对金融专业学生的风险偏好调查，利用前景理论对风险偏好进行了量化研究。本研究有利于金融专业学生了解和掌握风险偏好理论和前景理论，有利于学生了解自己的风险偏好态度，更形象地理解前景理论和风险偏好理论，提高风险意识。

参考文献

［1］Kenneth J.Arrow：Aspects of the Theory of Risk Bearing［M］.Hlesinki：Academic Bookstore，1965.

［2］JV Neumann、O Morgenstem：Theory of Games and Economic Behavior［M］.Princeton University Press，1944.

［3］Amos Tversky、Daniel Kahneman：Advances in Prospect Theory：Cumulative Representation of Uncertainty［J］.Journal of Risk and Uncertainty，1992（5）.

（责任编辑：胡冬梅）

基金项目：湖南省教育规划课题，金融专业学生风险意识培养与职业伦理教育研究，编号：XJK013Q GD005。