局部环及其扩张的强二和性质

唐高华，吴严生，张恒斌，李　玉

(广西师范学院数学与统计科学学院，广西南宁530023)



局部环及其扩张的强二和性质

唐高华，吴严生，张恒斌，李玉

(广西师范学院数学与统计科学学院，广西南宁530023)

摘要：称环R的元有强二和环性质如果它可以写成该环中两个可换单位的和。如果环R的每个元都有强二和性质，则称R为强二和环。局部环是非常重要的环类，局部环及其扩张在环论、模论和同调代数等的研究中都有非常重要的地位。本文首先给出了局部环是强二和环的一个刻画，然后研究了局部环的幂级数扩张、平凡扩张和矩阵扩张等的强二和性。

关键词：2-good 环；强二和环；局部环；环扩张

本文考虑的都是有单位元的结合环。设R是一个环，用U(R)、J(R)和C(R)分别表示环R的单位群、Jacobson根和中心。设M是R-模，EndR(M)表示M的自同态环。环R上的n阶全矩阵环和n阶上三角矩阵环分别用Mn(R) 和Tn(R) 表示，单位矩阵用E表示。集合X的基数用|X|表示。

Wolfson和Zelinsky分别在文献[1-2]中用不同的方法证明了以下定理：

Wolfson-Zelinsky定理：设V是除环D上的向量空间，若D≠F2或dim(V)≠1，则V上任一线性变换可以写成两个可逆线性变换的和。

这一结果使得研究由单位生成的环成为环论中的热门问题[3-9]。2005年，Vámos[3]将具有上述性质的环定义为2-good环，即如果环R中每个元可以写成该环中两个单位的和则称R为2-good环。该文证明了2-good环的许多环论性质并给出了一系列2-good环的例子。2013年，唐高华和周毅强[5]首次给出了强二和环的定义：环中每个元都可以写成环中两个可交换单位的和。该文主要证明了以下定理：

Tang-Zhou定理：除环D上的向量空间V上的线性变换环是强二和环当且仅当|D|≥3且dim(V)<∞。

显然强二和环是2-good环，但由Wolfson-Zelinsky定理和Tang-Zhou定理知Mn(Z2)(n≥2)是2-good环但不是强二和环。

局部环是非常重要的环类，局部环及其扩张在环论、模论和同调代数等的研究中都有非常重要的地位。本文首先给出局部环是强二和环的一个刻画，然后研究局部环的幂级数扩张、平凡扩张、矩阵扩张等的强二和性。特别地，对于交换局部环R，我们证明Mn(R)(n=2或3)是强二和环当且仅当R是强二和环。我们猜想此结论对任意的正整数n也成立。

1相关引理

引理1(文献[5]引理2)①设环R是强二和环，则R的同态像也是强二和环；②设R=∏α∈ΛRα是环的直积，则R是强二和环当且仅当每个Rα都是强二和环。

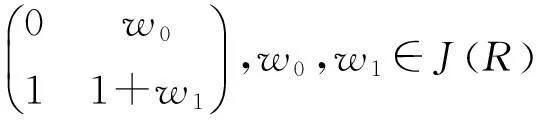
2主要结果

定理1若R是局部环，则R是强二和环当且仅当对任意a∈J(R)，C(a)∩U#(R)≠∅，这里C(a)={x∈R|xa=ax}，U#(R)=U(R)(1+J(R))={a∈U(R)|a∉1+J(R)}。

证明(⟸)。对R中元素分两种情况讨论。

情形1：x∈J(R)或U#(R)。则x有强二和分解：x=(x-1)+1。

情形2：x=1+a∈1+J(R)。取u∈C(a)∩U#(R)，则(u+a)，(1-u)∈U(R)且(u+a)(1-u)=(1-u)(u+a)。于是x有强二和分解：x=1+a=(u+a)+(1-u)。

(⟹)。∀a∈J(R)，1+a有强二和性质。设1+a=u+(1+a-u)是其强二和分解，则1+a-u，u∈U(R)且au=ua。故u∈C(a)∩U#(R)。证毕。

推论1设R是交换局部环，则R是强二和环⟺U#(R)≠∅⟺R/J(R)Z2。

设R是环且σ：R→R是一环的自同态。R上的斜幂级数环R[[x，σ]]的所有元素是系数取自R的x的形式幂级数，环中加法是平凡的，乘法定义为：对r∈R，xr=σ(r)x。特别地，R[[x]]=R[[x，1R]]是R上的形式幂级数环。

定理2设R是局部环，若存在u∈C(R)∩U#(R)使得σ(u)=u，则R[[x，σ]]是强二和环。

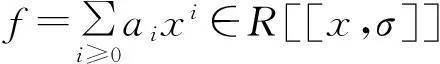
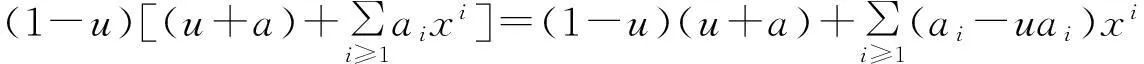
(1)

(2)

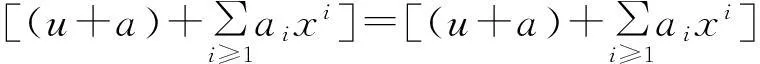
推论2设R是局部环。若C(R)∩U#(R)≠∅，则R[[x]]是强二和环。

例1设F是一特征为2的有限域且|F|=2k>2。若R=F2k[[x，σ]]且σ：F2k→F2k，σ(a)=a2，∀a∈F2k，则R不是强二和环。

设R是环，M是(R，R)-双模。R的M平凡扩张S：=R∝M的元素集为R×M，加法是通常的加法，乘法定义为：对r，r′∈R，m，m′∈M，(r，m)(r′，m′) =(rr′，rm′+mr′)。

定理3设R是局部环，若C(R)∩U#(R)≠∅，则S=R∝R是强二和环。

证明显然U(S)={(u，v)|u∈U(R)，v∈R}。任取(a，b)∈S，若a∈J(R)或U#(R)，则(a，b)=(a-1，b)+(1，0)是(a，b)的强二和分解。若a=1+c∈1+J(R)，则存在u∈C(R)∩U#(R)使得a=1+c=(u+c)+(1-u)是a的强二和分解。所以(a，b) =(u+c，b)+(1-u，0)是强二和分解。证毕。

定理4设D是除环，则S=D∝D是强二和环当且仅当DZ2。

证明(⟸)。设(a，b)∈S。若a≠1，则有强二和分解(a，b)=(a-1，b)+(1，0)；若a=1，b=0或1，取1≠x∈U(D)，则(1，b)=(1-x，b-x)+(x，x)是强二和分解；若a=1，b≠0，1，则(1，b)=(1-b，0)+(b，b)是强二和分解。

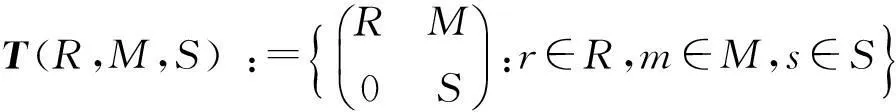
定理5设R、S都是局部环，若下面两个条件都满足，则T(R，M，S)是强二和环。

(Ⅰ)对任意m∈M，存在u∈C(R)∩U#(R)和v∈C(S)∩U#(S)使得um=mv；

(Ⅱ)若r∈J(R)，s∈1+J(S)，m∈M，则存在x∈M使得m=xs-rx。

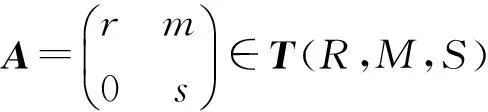
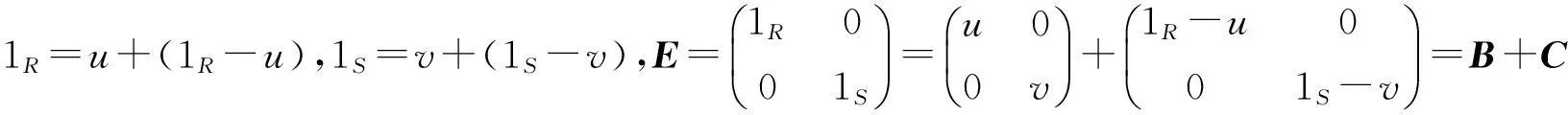
情形2：r∈J(R)，s∈J(S)。则A在T(R，M，S)中有强二和分解：A=E+(A-E)。

推论3设R是交换局部环，则T2(R)是强二和环当且仅当R是强二和环。

证明(⟸)。由于R是交换局部强二和环，易见它满足定理5的条件，从而结论成立。

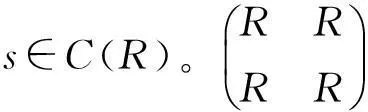
定理6设R是局部环且s∈C(R)∩J(R)，若C(R)∩U#(R)≠∅，则Ks(R)是强二和环。

证明设A∈Ks(R)，由引理3可以分成以下4种情况讨论：

情形1：A可逆。存在a∈C(R)∩U#(R)使得a-1∈U(R)。所以A=aA+(1-a)A。

情形2：E-A可逆。所以A=E+(A-E)。

定理7设R是局部环，若C(R)∩U#(R)≠∅，则M2(R)是强二和环。

证明设A∈M2(R)，由引理4可以分成以下3种情况讨论：

情形1：A可逆。取u∈C(R)∩U#(R)，则u-1∈U(R)。所以A=uA+(1-u)A是其在M2(R)中的强二和分解。

情形2：E-A可逆。故A=E+(A-E)是其在M2(R)中的强二和分解。

推论4设R是交换局部环，则M2(R)是强二和环当且仅当R是强二和环。

(⟸)。因为R是强二和环，则U#(R)≠∅。由定理7，M2(R)是强二和环。

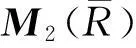
定理8设R是交换局部环，则M3(R)是强二和环当且仅当R是强二和环。

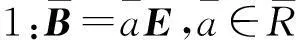
①若β，γ∈J(R)且α∈U#(R)，则E-C可逆，C=E+(C-E)是一强二和分解。

③若α，β，γ∈U(R)，则C可逆，且C=uC+(1-u)C是强二和分解。

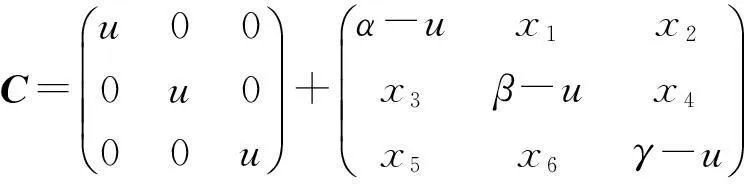
(⟹)。类似于推论4的必要性证明。证毕。

猜想1设R是交换局部环，n是正整数，则Mn(R)是强二和环当且仅当R是强二和环。

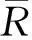
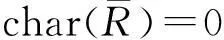
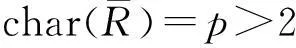
定理10的证明与定理9的证明类似，省略。

参考文献：

[1]WOLFSON K G. An ideal-theoretic characterization of the ring of all linear transformations[J]. American Journal of Mathematics，1953，75(2)： 358-386. DOI:10.2307/2372458.

[2]ZELINSKY D. Every linear transformation is a sum of nonsingular ones[J]. Proceedings of the American Mathematical Society，1954，5(4)： 627-630. DOI:10.2307/2032048.

[4]SRIVASTAVA A K. A survey of rings generated by units[J]. Ann Fac Sci Toulouse Math，2010，19(s1)： 203-213. DOI:10.5802/afst.1281.

[5]TANG Gaohua，ZHOU Yiqiang. When is every linear transformation a sum of two commuting invertible ones ?[J]. Linear Algebra and Its Applications，2013，439(11)： 3615-3619. DOI:1016/j.laa.2013.09.038.

[6]GROVER H K，WANG Zhou，KHURANA D，et al. Sums of units in rings[J]. Journal of Algebra and Its Applications，2014，13(1):1350072. DOI:10.1142/s0219498813500722.

[7]唐高华，苏华东，易忠.Zn[i]的单位群结构[J]. 广西师范大学学报(自然科学版)，2010，28(2)： 38-41. DOI:10.16088/j.issn.1001-6600.2010.02.004.

[8]唐高华，赵淼清，佟文廷. 关于凝聚局部环的正则性[J]. 数学学报，2000，43(4):615-622.

[9]李先贤，程福长. 非交换 Gr-凝聚半局部环的同调维数[J]. 广西师范大学学报(自然科学版)，1998，16(2)： 13-17. DOI:10.16088/j.issn.1001-6600.1998.02.003.

[10]TANG Gaohua，ZHOU Yiqiang. Strong cleanness of generalized matrix rings over a local ring[J]. Linear Algebra and Its Applications，2012，437(10)： 2546-2559. DOI:10.1016/j.laa.2012.06.035.

[11]YANG Xiande，ZHOU Yiqiang. Strong cleanness of the 2×2 matrix ring over a general local ring[J]. Journal of Algebra，2008，320(6)： 2280-2290. DOI:10.1016/j.jalgebra.2008.06.012.

[12]AVNI N，ONN U，PRASAD A，et al. Similarity classes of 3×3 matrices over a local principal ideal ring[J]. Communications in Algebra，2009，37(8)： 2601-2615. DOI:10.1080/00927870902747266.

[13]KRYLOV P A. Isomorphism of generalized matrix rings[J]. Algebra and Logic，2008，47(4)： 258-262. DOI:10.1007/s10469-008-9016-y.

(责任编辑黄勇)

Strong 2-sum Property of Local Rings and Their Extensions

TANG Gaohua，WU Yansheng，ZHANG Hengbin，LI Yu

(School of Mathematics and Statistics，Guangxi Teachers Education University， Nanning Guangxi 530023，China)

Abstract:An element of a ring R is called to have the strong 2-sum property if it is a sum of two units that commute with each other. And a ring R is called a strong 2-sum ring if every element of R has the strong 2-sum property. Local ring is a very important class of rings. Local rings and their extensions are very important in the research of ring theory，module theory and homological algebra. In this article， a characterization of a local ring to be a strong 2-sum ring is given. Then, the strong 2-sum property of local rings and their power series extension，trivial extension and matrix extension are studied.

Keywords:2-good ring；strong 2-sum ring；local ring；ring extension

中图分类号：O153.3

文献标志码：A

文章编号：1001-6600(2016)01-0072-06

基金项目：国家自然科学基金资助项目(11161006，11461010)；广西科学研究与技术开发项目(桂科合1599005-2-13)；广西高校科学技术研究项目(KY2015ZD075)。

收稿日期：2015-08-23

doi:10.16088/j.issn.1001-6600.2016.01.011

通信联系人：唐高华(1965—)，男，广西桂林人，广西师范学院教授，博士，博导。E-mail：tanggaohua@163.com