时空Kriging在局域地磁场分析中的应用

陈鼎新，刘代志，孟　亮，李义红，杨晓君

(火箭军工程大学907教研室，陕西西安710025)



时空Kriging在局域地磁场分析中的应用

陈鼎新，刘代志，孟亮，李义红，杨晓君

(火箭军工程大学907教研室，陕西西安710025)

摘要：地磁场在空间上和时间上具有连续性和相关性，考察时间特性对于地磁场分析精度的影响，是本文的目的。本文以宁夏周围局域地磁场秒数据为研究对象，应用时空Kriging函数进行插值计算，采用Product-Sun模型结合时间和空间信息，使得插值精度大幅度提高。用空间域方法的最近邻、V4样条插值和Kriging方法进行对比的结果表明，由于充分利用了时间域信息，时空Kriging精度更高。本文还分析了其高精度的原因，并对时空插值过程中数据库容量的选择进行讨论。

关键词：地磁场；时空Kriging；交叉验证；变差函数

时空Kriging在分析连续变化的自然特征量时，具有明显的优势。研究者已经将时空Kriging成功应用于空气质量检测[6-7]、降雨量建模[8]、风力数据插值[9]、地下水位分析[10-11]等领域，该方法能够利用时间相关性提高分析精度。而在地磁场的分析中，目前仍没有学者应用时空Kriging。

笔者曾初步探讨过时间域信息对地磁场插值的改进，本文针对地磁场数据，进一步研究用时空Kriging方法进行插值所涉及的一些问题，如精度提高的原因、时空插值过程中数据库容量的选择等。

1方法原理

Kriging方法是以南非矿业工程师D. G. Krige (克里金)名字命名的一项实用空间估计技术，是地质统计学的重要组成部分。假设在待估计点x的临域内共有n个实测点，即x1,x2,…，xn，其样本值为Z(xi)。General Kriging的插值公式为：

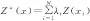
(1)

定义变差函数：

(2)

通过解Kriging方程组

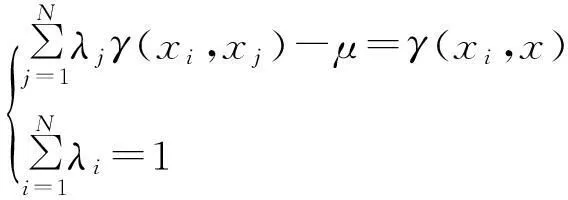
(3)

算出权重系数λ，进而由式(1)得到Z*(x)的值。

时空Kriging是在Kriging算法的基础上，引入时间域的连续性与相关性。用A=(si,tj)表示时空域中某一点的坐标，则该点处特征量的值可以表示为邻域内所有点的加权和[6]：

(4)

饱和输出灰度值随电子注量的变化规律，如图3所示，不同辐照偏置条件下器件的退化趋势相似，即随电子注量增加饱和输出灰度值不断减小,说明饱和输出灰度值对电离总剂量敏感。

(5)

则可以通过Kriging方程组

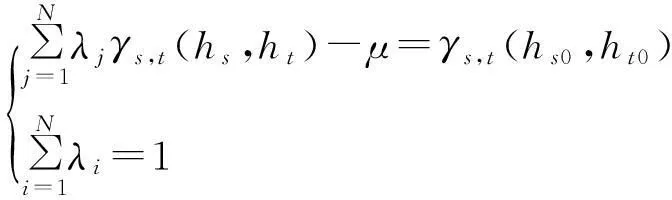
(6)

来求解λ。现实中，由于时间和空间中变量的量纲不同，时空联合与域距离很难统一表示，直接求变差函数的时空联合分布是困难的[12]。然而，通过一些典型的模型，例如Product-Sum[13-15]、Product- Integration[16-17]及Cressie-Huang[18]模型等，可以用时间域条件分布函数和空间域条件分布函数

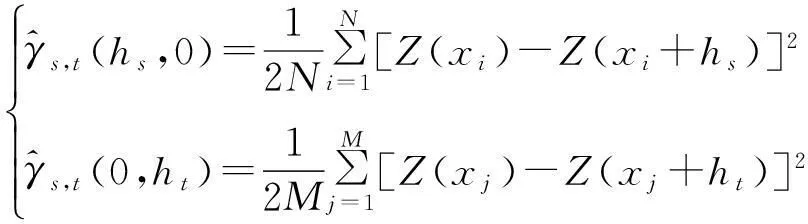
(7)

来表示时空域的变差函数[18]

γs,t(hs,ht)=F(γs,t(hs,0),γs,t(0,ht))。

(8)

2实验分析

2.1数据来源

实验采用的数据，是宁夏周围6个地磁观测台站2009年2月14日的地磁场秒数据序列。台站位置如图1所示，覆盖了经度103.0°E～104.2°E，纬度35.6°N～37.3°N的范围。在地磁导航等应用中通常将地磁信号的Z分量作为地磁匹配分量[18]，因此，本文选择地磁Z分量作为研究对象，对一天中地磁场数据进行区域插值[19]。

2.2时空变差函数构建

用式(7)估计空间域和时间域的条件变差函数，并进行拟合。通常用到的拟合函数有sphere函数、index函数、Gauss函数等[6]。首先从变差函数估计值的分布形状判断，空间域变差函数接近于sphere分布，时间域变差函数符合index分布。再利用估计值，分别对参数进行拟合，空间域变差函数和时间域变差函数分别为：

(9)

(10)

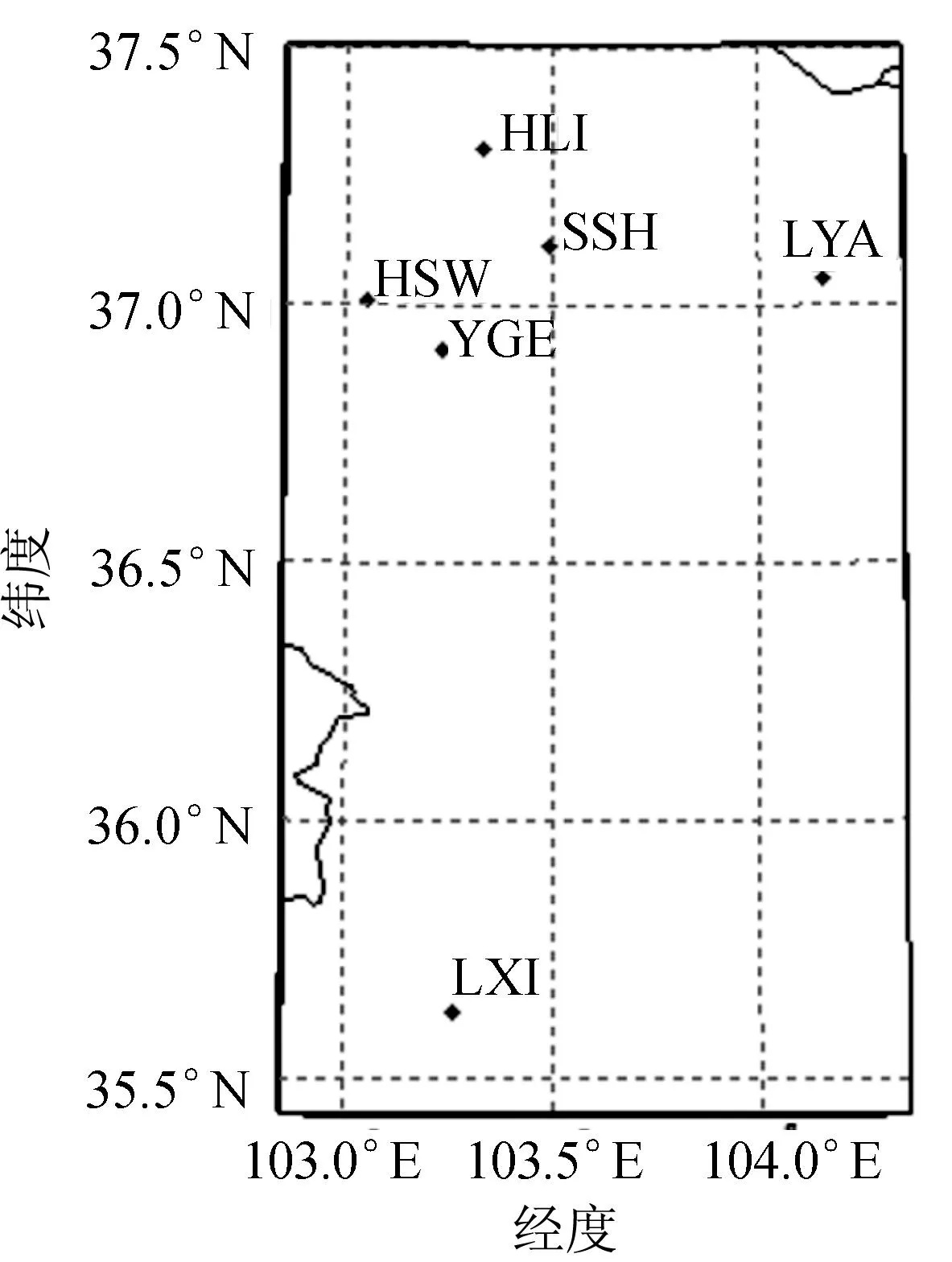
图1　台站分布图Fig.1　Illustration of monitoring stations

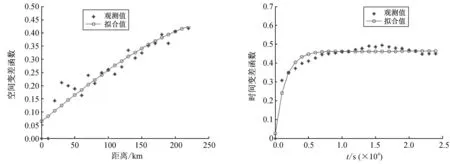
图2　条件变差函数的拟合结果Fig.2　Illustration of fitted variogram funtions

拟合过程如图2所示。参照式(7)，利用条件分布函数来构建时空域变差函数如图3所示。本文采用Product-Sum模型进行计算，模型计算公式为[13-15]：

γst(hs,ht)=(k1Ct(0)+k2)γs(hs)+(k1Cs(0)+k3)γt(ht)-k1γs(hs)γt(ht)，

其中：Cs(0)=nuggets+sills；Ct(0)=nuggett+sillt；Cst(0)取实验变差函数的最大值0.494 6[15]。得到时空变差函数：

γst(hs,ht)=γs(hs)+γt(ht)-0.494 6γs(hs)γt(ht)。

2.3结果分析

对观测台站进行交叉验证实验。实验中，计算某一时刻t的值，用其前60 s的观测量建立数据库，即用区间[t-60,t-1]内的所有值进行分析。性能的检验标准是误差统计量mean absolute error (MAE)和root mean square error (RMSE)

对一天中每一个准点时刻进行交叉验证实验并记录结果。用V4、最近邻[20]、Kriging等空间域插值方法进行对比，结果如图4所示。相对于空间域插值方法，时空Kriging的插值精度有了大幅度的提高。无论MAE还是RMSE，时空Kriging的误差都远小于空间域方法，精度明显提高。

图4　交叉验证的误差统计量分析Fig.4　Statistics of cross validation

将各时间点的MAE和RMSE进行时间域的加权平均，结果如表1所示。时空Kriging的时间域误差统计量远小于其他方法，表明时空Kriging在进行插值的24个整点时间处，计算精度总体较高。时间域信息的加入，大大提高了插值的总体精度。而精度大幅度的提高，也得益于所用数据的高时间分辨率。实验数据为地磁场的秒数据，分辨率达到秒级。CM4模型的时间分辨率是6 h。相比于CM4模型，我们的模型时间采样更密集，时间信息更丰富，因此时空Kriging的精度也越高。

表1　误差统计量的时间域平均

2.4时空Kriging数据库容量的讨论

对t时刻进行插值时，用到了[t-n,t-1]的先验知识，其中时间长度n的大小即数据库容量。图5中记录了不同数据库容量下，时空Kriging插值误差的时间域均值。从图中可以看出，数据库容量为零时，时空Kriging的插值误差在101数量级，与普通的空间域插值方法无异；数据库容量从0到1的过程中，时空Kriging的插值误差出现大幅下降，达到10-2数量级。数据库容量为0，即计算t时刻数据时，只用到了当前时刻的值，并没有利用先验知识，此时的时空Kriging退化为空间域的Kriging方法。从容量为1开始，历史信息被加入时空Kriging的计算过程，先验知识提高了插值的精度，而数据的高时间分辨率以及时间相关性，使得时空Kriging插值的精度提高幅度较大。

图5　时空Kriging数据库对性能的影响Fig.5　Influence of data base to Spatiotemporal Kriging

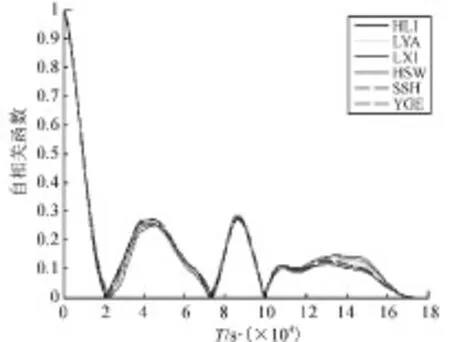
图6　各台站数据的自相关函数Fig.6　Autocorrelation of data in each station

从图5中可以看到，随着数据库容量的增大，时空Kriging的插值误差增大，最终维持在某一稳定值。如图6所示，数据的时间相关性随着时间增加而减小。当数据库容量增大时，相关性较小的先验知识被加进数据库，在一定程度上干扰了插值，降低精度。在时间域距离达到某一个值后，超出邻域范围的点在计算过程中将不予考虑，因此，图4中曲线最终维持在某一固定值。

3结论

地磁场是一种随空间、时间变化的物理量，在时间上具有连续性和相关性。因此在分析过程中，考虑时间域的相关性可以提高插值精度。时空Kriging可以有效地利用时间域的先验知识，改进插值的性能。本文将时空Kriging应用于地磁场分析领域，采用Product-Sum模型结合时间和空间信息，使得插值精度大幅度提高。分析了时空Kriging获得高精度的原因，即数据的高时间分辨率，并讨论了数据库容量对时空Kriging算法的影响。结果表明，地磁场分析过程中，运用时空Kriging可以充分利用时间域信息获得高精度，比空间域插值算法更有优势。

参考文献：

[1]徐文耀. 地磁学[M]. 北京：地震出版社，2003： 35.

[2]徐文耀．地球电磁现象物理学[M]．合肥：中国科学技术大学出版社，2009： 473-474.

[3]袁杨辉. 地磁导航中地磁变化场的研究[D]. 武汉：华中科技大学，2012： 18-19.

[4]牛超，卢世坤，祁树锋. 基于EEMD和改进ELMAN神经网络的地球变化磁场短时预测[J]. 河北师范大学学报(自然科学版)，2014，38(1)： 50-54.

[5]DU Ruiqing，YANG Jin. Application of ordinary kriging method in data processing of magnetic survey[C]//The 7th International Conference on Computer Science & Education (ICCSE 2012). Melbourne，Australia. USA：IEEE Computer Society，2012:771-774.

[6]LACO S D， MYERS D E，POSA D. The linear coregionalization model and the product-sum space-time variogram[J]. Mathematical Geology，2003，35(2)： 25-38.

[7]NUNES C, SOARES A. Geostatistical space-time simulation model for air quality prediction[J]. Environmetrics，2005，16 ：393，404

[8]LI Sha， SHU Hong， XU Zhengquan. Spatial-temporal statistics and analysis of rainfall in jilin province[C]//International Workshop on Computer Science for Environmental Engineering and EcoInformatics (CSEEE 2011). Berlin: Springer-Verlag， 2011：255-261.

[9]GNEITING T. Nonseparable，Stationary covariance functions for space-time data[J]. Journal of the American Statistical Association，2002，97(458)： 590-600.

[10]HEUVELINK G B M. Ana Lucia Berretta Hurtado，Quirijn de Jong van Lier. Spatio-temporal variability of soil water tension in a tropical soil in Brazil[J]. Geoderma，2005，133(3/4)： 231-243.

[11]LARKA R M， BELLAMY P H，RAWLINS B G. Spatio-temporal variability of some metal concentrations in the soil of eastern England，and implications for soil monitoring[J]. Geoderma，2006，133： 363-379.

[12]王建民，张 锦，邓增兵，等. 时空Kriging插值在边坡变形监测中的应用[J]. 煤炭学报，2014，39(5)： 874-879.

[13]DE CESARE L，MYERS D E，POSA D. Product-sum covariance for space-time modeling，an environmental application[J]. Environmetrics，2001，12：11-23.

[14]CESARE D E，MYERS D E，POSA D. Estimating and modeling space-time correlation structures[J]. Stat Probab Lett，2001，51(1)：9-14.

[15]李莎，舒红，董林. 基于时空变异函数的Kriging插值及实现[J]. 计算机工程与应用，2011，47(23)： 25-38.

[16]IACO S. D， MYERS D E， POSA D. Nonseparable space-time covariance models： some parametric families[J]. Mathematical Geology, 2002，34(1)： 23-42.

[17]李莎，舒红，徐正全. 利用时空Kriging进行气温插值研究[J]. 武汉大学学报(信息科学版)，2012，37(2)： 237-241.

[18]CRESSIE N, HUANG H C. Classes of nonseparable，spatio-temporal stationary covariance functions[J]. Journal of the American Statistical Association，1999，94，1330-1340.

[19]农吉夫，黄文宁. 基于主成分分析的BP神经网络长期预报模型[J]. 广西师范大学学报(自然科学版)，2008，26(4)： 46-51.

[20]王珏，石纯一. 机器学习研究[J]. 广西师范大学学报(自然科学版)，2003，21(2)： 1-15.

(责任编辑李小玲)

Applications of Spatiotemporal Kriging in Local Geomagnetic Field Analysis

CHEN Dingxin, LIU Daizhi, MENG Liang, LI Yihong, YANG Xiaojun

(PLA Rocket Force Engineering University, Xi’an Shaanxi 710025, China)

Abstract:Geomagnetic field has continuity and relativity, and the influence of time characteristics on the analysis precision of geomagnetic field is the aim of this paper. Based on the local geomagnetic field data in Ningxia, China, we use the spatial and temporal Kriging function to carry out interpolation calculation. Spatiotemporal Kriging is the extension of Kriging method in space-time domain, including simulation of conditional variation function, construction of space time variation function, cross validation and so on. According to the experiment results, due to the full use of space-time information, Spatiotemporal Kriging outperforms space-only methods, such as the nearest, V4 and Kriging methods. The reason for improvement of accuracy is analyzed, and the selection of database capacity in the process of spatial and temporal interpolation. is discussed.

Keywords:geomagnetic field; spatiotemporal Kriging; cross validation; variogram

中图分类号：P318.2

文献标志码：A

文章编号：1001-6600(2016)01-0038-07

基金项目：国家自然科学基金资助项目(41374154，61304240)；中国博士后科学基金资助项目(2014M552589)

收稿日期：2015-05-14

doi:10.16088/j.issn.1001-6600.2016.01.006

通信联系人：刘代志(1960—)，男，湖南醴陵人，火箭军工程大学教授，博士。E-mail：ldzpwt@163.com