对一道初中数学综合题的探究

□浙江省开化县教育局教研室 严生明　　□浙江省常山县城关中学 王亚君



对一道初中数学综合题的探究

□浙江省开化县教育局教研室 严生明□浙江省常山县城关中学 王亚君

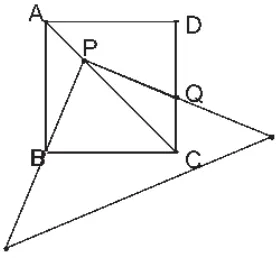
原题呈现：把一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q.

探究：设A、P两点间的距离为x.

⑴如图，当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察到的结论。

⑵当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由。

本题涉及等腰三角形、直角三角形、全等三角形、正方形、平移变换等初中数学核心知识，涉及几何直观、运算能力、推理能力等核心概念，同时它还渗透了分类讨论、数形结合、从特殊到一般等重要数学思想方法，故本题是一道能较好考查学生对初中数学知识掌握情况的题目。同时，本题还展现了一个数学问题研究的全过程：从问题的提出、探究与发现、实验与验证到猜想与证明。学生正确解答本题既可以完整地经历问题的提出、探究、发展的全过程，又可以充分体验感受从特殊到一般、猜想等一般性数学方法，较好地考查了学生运用数学思想方法探索规律、获取新知的能力，以及运用知识解决问题的能力。

1．本题解决的策略分析。数学题目的解决策略，是指探求数学题目的答案时所采取的途径和方法。方法是有层次性的，题目解决的策略是最高层次的解题方法，是对解题途径的概括性的认识。根据著名数学家波利亚“怎样解题”表的提法，数学题目的解决过程可以分为四步：①弄清问题；②拟定计划；③实现计划；④回顾。

（1）第一问：当点Q在边CD上时，探究线段PQ与线段PB之间有怎样的大小关系？此例说明解题策略的产生过程。

第一环节，分析思考：由于点P在对角线AC上滑动，随着点P变化整个图形也发生变化，显然点Q也在运动，为此要探究线段PQ与线段PB之间的大小关系显得无从下手。我们知道认识事物时常从特殊性入手，如果我们在解题时也一样，从特殊情况着手会怎样？本题中，点P的特殊位置是什么？让学生自主探索，在得出点P的特殊位置后再分析这种情况下的点Q的位置，不难得出此时P与A重合，Q与D重合，所以PB=PQ。

第二环节，理清思路：经过前面的分析思考，不难得出线段PQ与线段PB之间的大小关系，于是猜想两条线段相等。

第三环节，验证思维：有许多学生在得到PB=PQ后就认为万事大吉，而猜想是否正确必须给予验证。要证两条线段相等，常用的方法是构造两个三角形证明全等或者构造一个三角形证明是等腰三角形。由于在平移过程中，直角始终保持不变，所以萌发了在对角线的两侧各做一条垂线试试，此时由于正方形对角线的特性易得到角两边的距离相等，再加上同角的余角相等易证三角形全等，从而问题得以解决。通过这样的思考，本小题才算正式完成。

（2）对于第二问：当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由。本小题主要考查分类讨论思想，要使△PCQ成为等腰三角形，从选哪条边为腰考虑分三种情况：PQ=PC、PQ=QC、CP=CQ；也可从位置讨论，分Q在DC边上和Q在DC的延长线上两种情况。

2.本题的解法。针对问题（1）有三种解法：

解法（1）：PB=PQ，证明如下：

如图⑴：过P分别作BC、CD的垂线，分别交BC、CD于点M、N，

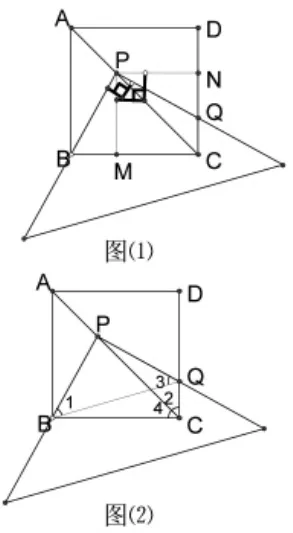
则∠PMB=∠PNQ=90°，∴∠NPM=90°，

又∵∠BPQ=90°，

∴∠BPM=∠QPN（同角的余角相等），

∵AC是正方形ABCD的对角线，

∴AC平分∠BCD，

∴PM=PN，

∴△PBM≌△PQN，

∴PB=PQ.

解法（2）：PQ=PB，证明如下：如图⑵，连接BQ，

∵∠BPQ=∠BCQ=90°，

∴P、B、C、Q四点共圆，

∴∠1=∠2，∠3=∠4，

又∵∠2=∠4=45°，∴∠1=∠3，

∴PQ=PB.

解法（3）：PQ=PB，如图⑶，过P点作MN∥BC分别交AB、DC于点M、N，

则∠PMB=∠PNQ=90°，

在正方形ABCD中，AC为对角线，

∴AM=PM，

又∵AB=MN，∴MB=PN，

∵∠BPQ=90°，∴∠BPM+∠NPQ=90°，

又∵∠BPM+∠MBP=90°，

∴∠NPQ=∠MBP，

∴Rt△MBP≌Rt△NPQ，

∴PQ=PB.

解法（2）比较特殊，学生较难想到；解法（1）、（3）的思路比较类似，都是构造直角三角形，利用同角的余角相等来证全等。

针对问题（2）也有三种解法：

解法（1）：分三种情况讨论：①PQ=QC，此时点Q与点D重合，x=0；②PQ=PC，此时不存在；③CP=CQ，此时Q在边DC的延长线上，如图⑷，

∵CP=CQ，∴∠2=∠1，

在Rt△BPE和Rt△QCE中，∠BOP=∠COQ，∴∠2=∠3，

∴∠1=∠3，

∵∠ABP=90°-∠3，

∠APB=180°-∠BPQ-∠1=180°-90°-∠1=90°-∠1，

∴∠APB=∠ABP，

∴AP=AB=1，即x=1.

综上所述，x=0，即点Q与点D重合时；或x=1，即Q在边DC的延长线上且时△PCQ为等腰三角形。

解法（2）：分两种情况讨论，Q在CD边上时，PQ=QC，此时点Q与点D重合，x=0；Q在CD的延长线上时，显然要使△PCQ成为等腰三角形，则只能CP=CQ.

如图⑸过P作AD的平行线分别交AB，CD于点E、F，则△AEP、△PCF都是等腰直角三角形，∴PF=CF=a，AE=EP=1-a

易证△PBE≌△QPF，∴PE=FQ.

∴CQ=FQ-FC=PE-FC=1-a-a=1-2a.

∴PC=CQ=1-2a.

在Rt△PCF中，PF2+FC2=PC2

∴a2+a2=（1-2a）2

综上所述，x=0，即点Q与点D重合时；或x=1，即Q在边DC的延长线上且时△PCQ为等腰三角形。

解法（3）：如图⑹∵AC是正方形的对角线，

∴∠ACD=45°，

∴∠PCQ=180-45=135°，

在Rt△BPE和Rt△QCE中，∠BEP=

∠CEQ，∴△BPE∽△QCE

∴∠PBE=∠CQE=22.5°

∴∠ABP=90°-∠PBC=90-22.5=67.5°

∴∠APB=180°-∠BAP-∠ABP=180-45-67.5=67.5°

∴∠APB=∠ABP=67.5°

∴△ABP为等腰三角形.

∴AP=AB=1

综上所述，x=0，即点Q与点D重合时，或x=1，即Q在边DC的延长线上且时△PCQ为等腰三角形。

解法（1）和（3）都是通过证明△ABP为等腰三角形，求x；解法（2）要用到第一问知识的迁移能力，先证全等再利用直角三角形的勾股定理求x。

3.本题的拓展变化与延伸反思。本题的拓展从初级、中级和高级这三个层次进行。

初级拓展：不改变条件，将结论稍加改变，这类变式可以让绝大部分同学运用刚才学习的方法解决新问题。

变式1：如图⑺，其他条件不变，当点Q在DC延长线上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察的结论。

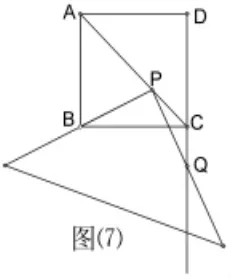
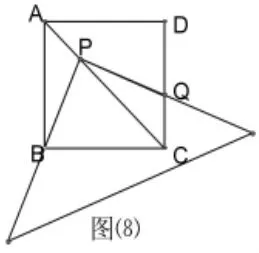
变式2：如图⑻，当点Q在边CD上时，四边形PBCQ的面积为y，AP的长为x，求y与x之间的函数解析式，并写出自变量的取值范围。

中级拓展：变换题目的某些条件和结论，引导学生一步一步往上爬.，学生总能“跳一跳摘到下一个苹果”，从而激发出强烈的探究欲望。

变式3：如图（9）：把一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P与正方形的中心O重合，让三角尺绕点O旋转，三角尺与正方形重叠的面积会如何变化？

变式4：如图（10）：把一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P与正方形的中心O重合，让三角尺绕点O旋转。三角尺的两边分别与AB、BC交于点M、N，连接BP，则线段BM、BN、BP之间存在怎样的关系？

高级拓展：通过增加或者减弱条件，改变图像等方法变式。突出了对新知识的迁移、运用，学生需要自己通过观察、分析、比较、概括、推理、判断等探索活动来解决新问题。

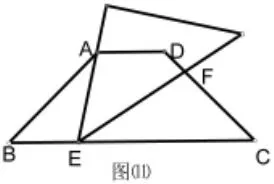
变式5：如图⑾，在等腰梯形ABCD中，AD∥BC，BC=∠B=45°，直角三角尺含45°角的顶点E在边BC上移动，一直角边始终经过点A，斜边与CD交于点F，若△ABE为等腰三角形，则CF=_______。

本题及其变式主要应用了从特殊到一般的思考方法，还有构造三角形证明全等或者相似。从学生熟悉而又简单的问题出发，通过不断演变，逐渐深入研究，不仅有利于消除学生学习的畏难情绪，让学生积极、主动地投入到数学学习中，而且有利于帮助学生全面系统复习已掌握的数学知识，有利于提高学生综合应用解决问题的能力。