高中数学三角函数教学要点分析

卢静

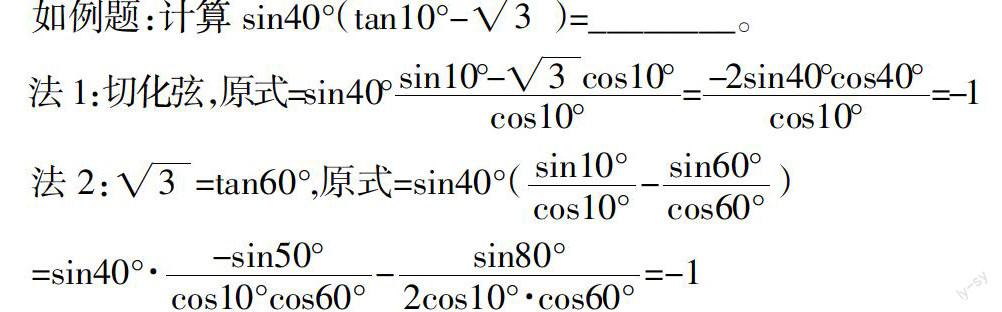
摘 要：在高中数学教学过程中，三角函数是非常重要的内容，也是学习中的难点。三角函数除了具有一般函数的各种性质外，还具有周期性及对称性，再结合系统丰富的三角公式，其产生的各种问题丰富多彩、层次分明、变化多端。在高中数学三角函数教学中，教师要注重把握教学要点，只有把握教学要点，才能提升教学的针对性，才能更有效地提升教学质量。

关键词：三角函数；记忆公式；恒等变形；图象；形式

在高中数学教学过程中，特别是在三角函数教学中，由于三角函数的性质比较多样化，教师要注重把握三角函数的教学重点，只有这样才能有效地提升教学质量，才能提升教学的针对性。

一、三角函数的恒等变形

在高中数学三角函数教学过程中，恒等变形是教学难点，也是教学重点。教师在讲解恒等变形时，要注重把握其教学要点，并明确三角函数恒等变形的应用。首先应该建构三角函数恒等变形的知识网络，确保学生明确三角函数的求值类型。在三角函数求值中，不同类型的求值方式不同，教师应该注重把握不同类型求值方式的异同，如“给角求值”“给值求值”等。教师还要注重把握恒等变形在具体运用过程中的注意事项，只有这样才能让学生真正学会三角函数的恒等变形。无论是简化三角函数的角度，还是证明不同角度之间的关联性，都应该在教学过程中注重把握角度的差异与联系，注重把握函数名称间的变换和联系，如升降幂，化切为弦等常用手段。

在这样的三角函数恒等变形的教学过程中，教师要引导学生仔细地分析题目，选择三角函数恒等变形中最合适、最直接的方法。在这类型题目中，切化弦是比较直接的方式，通过切化弦，能够将复杂的题目快速地转化为简单的题目，快速地进行题目解析，更有利于学生理解与把握题目。可见，在教学过程中，教师要注重把握三角函数恒等变形的重点，特别是让学生把握不同角度之间的关联，注重不同角度的差异，帮助学生理解三角函数的恒等变形。

二、三角函数的图象和形式

相比低年级数学，高中数学难度有所提升，教学侧重点也发生了转变。为了有效地帮助学生理解三角函数，教师要充分依托三角函数的性质、三角函数不同角度的差异，将抽象的内容形象化，通过数形转化来提升教学的质量，快速地帮助学生架构起理解的桥梁，只有这样才能真正帮助学生理解三角函数。

1.三角函数的区间

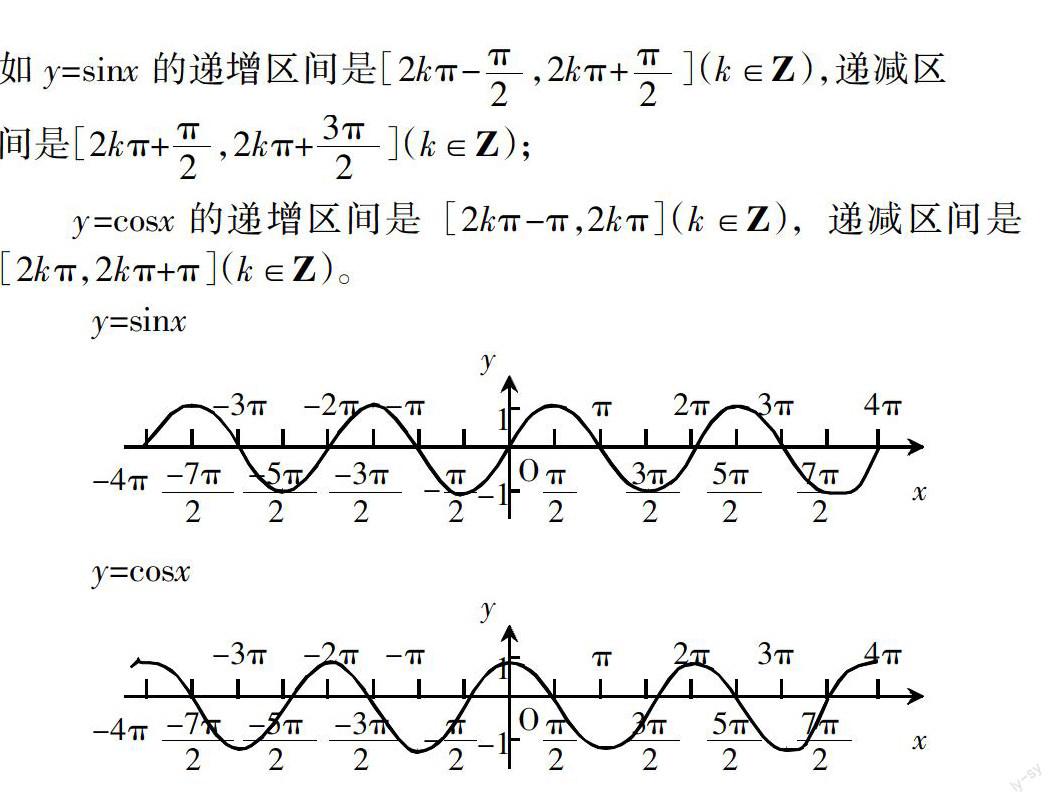
在高中数学教学过程中，三角函数的区间是三角函数的重要性质，是三角函数的重要内容。在把握三角函数的区间时，要注重引导学生理解与把握三角函数的递增或递减区间，明确不同区间的单调性，把握不同区间的递增方向，帮助学生更好地理解三角函数递增或递减的性质。不同三角函数的单调区间是不同的，很多学生在理解与把握的过程中，难免会混淆，这就要求教师要注重运用图形的方式来帮助学生形象化地理解不同三角函数的单调区间及区域。

2.三角函数的图象变换

三角函数的图象变换往往是基于y=sinx演变而来的，在此基础上衍生出了很多多样化的图象。所以在教学过程中，教师要注重引导学生扎实地理解与把握y=sinx等基本函数的特点，找准演变的规律，从而更好地了解三角函数。如在y=sinx的基础上，演变出来的新图象y=sin（ωx+φ），这是图象在值域或区间上的变化，在图象变化的过程中，往往存在两种典型的途径，不过这两种不同的途径在变化过程中方式不同，教师要引导学生注重把握其不同。

在图象变化的过程中，其通常采用的方式是平移，在平移的基础上根据不同的系数进行一定的伸缩变化。在具体的运用过程中，也往往采用相反的方式。无论哪种变形，请切记每一个变换总是对字母x而言，即图象变换要看“变量”起多大变化，而不是“角变化”多少。

参考文献：

刘文强.浅谈高中数学的三角函数教学[J].数学学习与研究，2014（09）.

编辑 赵飞飞