统计与概率考点与题型分析
2016-05-30李明伦
李明伦


统计与概率,是数学必修3的主要内容,也是新课标高考的必考内容,一般以一小(选择题或填空题)一大(解答题)的形式出现在高考试题中,难度中等.那么在新课标高考中,一般会出现哪些重要考点和基本题型呢?
一、随机抽样
考纲要求
(1)理解随机抽样的必要性和重要性.
(2)会用简单随机抽样方法从总体中抽取样本,了解分层抽样和系统抽样.
基本考点与题型
1. 简单的随机抽样
例1. 我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
A.134石 B.169石 C.338石 D.1365石
答案 B.
解析 设这批米内夹谷的个数为x,则由题意并结合简单随机抽样可知,=,解得x≈169,故应选B.
评注 本题以数学史为背景,重点考查简单的随机抽样及其特点,通过样本频率估算总体频率,难度不大.在高考中,考查简单的随机抽样的题目往往比较简单.
2. 系统抽样
例2.(2015·湖南)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.
若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是________.
答案 4.
解析 35÷7=5,因此可将编号为1~35的35个数据分成7组,每组有5个数据,在区间[139,151]上共有20个数据,分在4个小组中,每组取1人,共取4人.
评注 本题将系统抽样与茎叶图综合在一起考查,难度不大.对于系统抽样问题,我们要掌握两点:(1)分组的方法应依据抽取比例而定,即根据定义每组抽取一个样本;(2)起始编号的确定应用简单随机抽样的方法,一旦起始编号确定,其他编号便随之确定了.
3. 分层抽样
例3. 某学院的A,B,C三个专业共有1200名学生,为了调查这些学生勤工俭学的情况,拟采用分层抽样的方法抽取一个容量为120的样本,已知该学院的A专业有380名学生,B专业有420名学生,则在该学院的C专业应抽取学生________名.
答案 40.
解析 抽样比为=,∴A,B专业共抽取38+42=80名,
故C专业抽取120-80=40名.
评注 分层抽样是三种抽样方法中最重要的一种抽样方法,也是高考命题的热点,多以选择题或填空题的形式出现,试题难度不大,多为容易题或中档题,且主要有以下几个命题角度:一是计算某一层应抽取的样本数;二是求样本容量.
二、用样本估计总体
考纲要求
(1)了解分布的意义和作用,会列频率分布表,会画频率分布直方图、频率折线图、茎叶图,理解它们各自的特点.
(2)理解样本数据标准差的意义和作用,会计算数据标准差.
(3)能从样本数据中提取基本的数字特征(平均数、标准差),并给出合理解释.
(4)会用样本的频率分布估计总体的分布,会用样本的基本数字特征估计总体的基本数字特征,理解用样本估计总体的思想.
(5)会用随机抽样的基本方法和样本估计总体的思想解决一些简单的实际问题.
基本考点与题型
1. 频率分布直方图
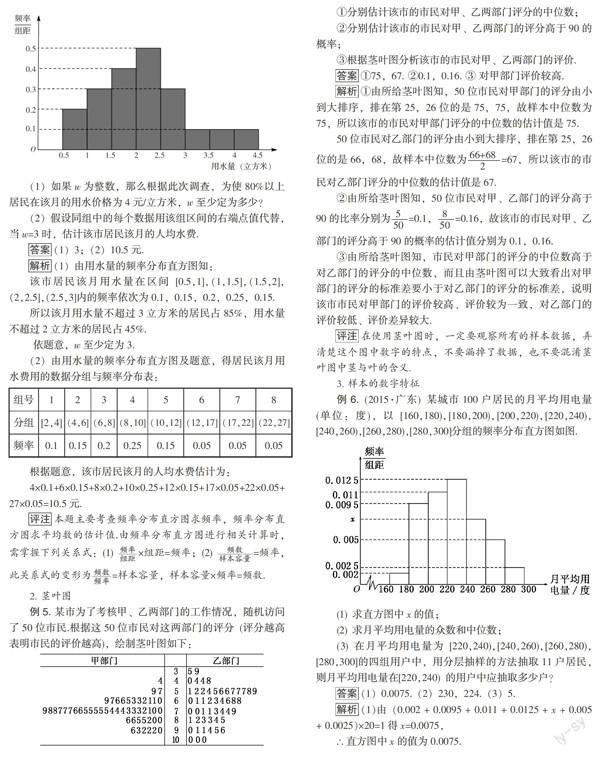
例4.(2016·北京)某市民用水拟实行阶梯水价,每人用水量中不超过w立方米的部分按4元/立方米收费,超出w立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
(1)如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费.
答案 (1)3;(2)10.5元.
解析 (1)由用水量的频率分布直方图知:
该市居民该月用水量在区间[0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3]内的频率依次为0.1,0.15,0.2,0.25,0.15.
所以该月用水量不超过3立方米的居民占85%,用水量不超过2立方米的居民占45%.
依题意,w至少定为3.
(2)由用水量的频率分布直方图及题意,得居民该月用水费用的数据分组与频率分布表:
根据题意,该市居民该月的人均水费估计为:
4×0.1+6×0.15+8×0.2+10×0.25+12×0.15+17×0.05+22×0.05+27×0.05=10.5元.
评注 本题主要考查频率分布直方图求频率,频率分布直方图求平均数的估计值.由频率分布直方图进行相关计算时,需掌握下列关系式:(1)×组距=频率;(2)=频率,此关系式的变形为=样本容量,样本容量×频率=频数.
2. 茎叶图
例5. 某市为了考核甲、乙两部门的工作情况,随机访问了50位市民.根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下:
①分别估计该市的市民对甲、乙两部门评分的中位数;
②分别估计该市的市民对甲、乙两部门的评分高于90的概率;
③根据茎叶图分析该市的市民对甲、乙两部门的评价.
答案 ①75,67. ②0.1,0.16. ③ 对甲部门评价较高.
解析 ①由所给茎叶图知,50位市民对甲部门的评分由小到大排序,排在第25,26位的是75,75,故样本中位数为75,所以该市的市民对甲部门评分的中位数的估计值是75.
50位市民对乙部门的评分由小到大排序,排在第25,26位的是66,68,故样本中位数为=67,所以该市的市民对乙部门评分的中位数的估计值是67.
②由所给茎叶图知,50位市民对甲、乙部门的评分高于90的比率分别为=0.1,=0.16,故该市的市民对甲、乙部门的评分高于90的概率的估计值分别为0.1,0.16.
③由所给茎叶图知,市民对甲部门的评分的中位数高于对乙部门的评分的中位数,而且由茎叶图可以大致看出对甲部门的评分的标准差要小于对乙部门的评分的标准差,说明该市市民对甲部门的评价较高、评价较为一致,对乙部门的评价较低、评价差异较大.
评注 在使用茎叶图时,一定要观察所有的样本数据,弄清楚这个图中数字的特点,不要漏掉了数据,也不要混淆茎叶图中茎与叶的含义.
3. 样本的数字特征
例6.(2015·广东)某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
答案 (1)0.0075.(2)230,224.(3)5.
解析 (1)由(0.002 + 0.0095 + 0.011 + 0.0125 + x + 0.005 + 0.0025)×20=1得x=0.0075,
∴直方图中x的值为0.0075.
(2)月平均用电量的众数是=230.
∵(0.002+0.0095+0.011)×20=0.45<0.5,
∴月平均用电量的中位数在[220,240)内,设中位数为a,则:
(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5,解得a=224,即中位数为224.
(3)月平均用电量在[220,240)的用户有0.0125×20×100=25户,
同理可求月平均用电量为[240,260),[260,280),[280,300)的用户分别有15户、10户、5户,
故抽取比例为=,
∴从月平均用电量在[220,240)的用户中应抽取25×=5户.
评注 样本的数字特征是每年高考的热点,且常与频率分布直方图、茎叶图等知识相综合考查.利用频率分布直方图求众数、中位数与平均数时,应注意这三者的区分:(1)最高的矩形的中点即众数;(2)中位数左边和右边的直方图的面积是相等的;(3)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
三、变量间的相关关系
考纲要求
(1)会作两个相关变量的散点图,会利用散点图认识变量之间的相关关系.
(2)了解最小二乘法的思想,能根据给出的线性回归系数公式建立线性回归方程.
基本考点与题型
1. 相关关系的判断
例7. 为研究语文成绩和英语成绩之间是否具有线性相关关系,统计某班学生的两科成绩得到如图所示的散点图(x轴、y轴的单位长度相同),用回归直线方程=bx+a近似地刻画其相关关系,根据图形,以下结论最有可能成立的是( )
A. 线性相关关系较强,b的值为1.25
B. 线性相关关系较强,b的值为0.83
C. 线性相关关系较强,b的值为-0.87
D. 线性相关关系较弱,无研究价值
答案 B.
解析 由散点图可以看出两个变量所构成的点在一条直线附近,所以线性相关关系较强,且应为正相关,所以回归直线方程的斜率应为正数,且从散点图观察,回归直线方程的斜率应该比y=x的斜率要小一些,综上可知应选B.
评注 相关关系的直观判断方法就是作出散点图,若散点图呈带状且区域较窄,说明两个变量有一定的线性相关性,若呈曲线型也是有相关性,若呈图形区域且分布较乱则不具备相关性.
2. 线性回归方程
例8.(2014·重庆)已知变量x与y正相关,且由观测数据算得样本平均数=3,=3.5,则由该观测数据算得的线性回归方程可能为( )
A. =0.4x+2.3 B. =2x-2.4
C. =-2x+9.5 D. =-0.3x+4.4
答案 A.
解析 依题意知,相应的回归直线的斜率应为正,排除C,D.
且直线必过点(3,3.5)代入A,B,得A正确.
评注 回归直线方程 = x+必过样本点中心(,).
四、随机事件的概率
考纲要求
(1)了解随机事件发生的不确定性和频率的稳定性,了解概率意义以及频率与概率的区别.
(2)了解两个互斥事件的概率加法公式.
基本考点与题型
1. 随机事件概率的求法
例9. 随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
解析 (1)在容量为30的样本中,不下雨的天数是26,以频率估计概率,4月份任选一天,西安市不下雨的概率为=.
(2)称相邻的两个日期为“互邻日期对”(如,1日与2日,2日与3日等).这样,在4月份中,前一天为晴天的互邻日期对有16个,其中后一天不下雨的有14个,所以晴天的次日不下雨的频率为. 以频率估计概率,运动会期间不下雨的概率为.
评注 本题主要考查随机事件的概率与频率的关系和随机事件概率的求法:(1)频率反映了一个随机事件出现的频繁程度,频率是随机的,而概率是一个确定的值,通常用概率来反映随机事件发生的可能性的大小,有时也用频率来作为随机事件概率的估计值.(2)利用概率的统计定义求事件的概率,即通过大量的重复试验,事件发生的频率会逐渐趋近于某一个常数,这个常数就是概率.
2. 互斥事件与对立事件的概率
例10. 甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则甲不输的概率为( )
答案 A.
解析 不输包括和棋与获胜两种情形,故甲不输概率为+=.
评注 运用概率加法的前提是事件互斥,不输包含赢与和,两种互斥,可用概率加法,本题属于简单题.
五、古典概型
考纲要求
(1)理解古典概型及其概率计算公式.
(2)会计算一些随机事件所含的基本事件及事件发生的概率
基本考点与题型
1. 简单的古典概型
例11. 小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M,I,N中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是( )
答案 C.
解析 开机密码的可能有:
(M,1),(M,2),(M,3),(M,4),(M,5),(I,1),(I,2),(I,3),(I,4),(I,5),(N,1),(N,2),(N,3),(N,4),(N,5)共15种可能,
所以小敏输入一次密码能够成功开机的概率是.
评注 作为客观题形式出现的古典概型试题,一般难度不大,解答常见错误是在用列举法计数时出现重复或遗漏,避免此类错误发生的有效方法是按照一定的标准进行列举.
2. 复杂的古典概型
例12. 某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
(1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3. 现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.
根据题意,这些基本事件的出现是等可能的.
事件“A1被选中且B1未被选中”所包含的基本事件有:{A1,B2},{A1,B3},共2个.
因此A1被选中且B1未被选中的概率为P=.
评注 此类问题一般以解答题的形式出现,基本方法有:(1)将所求事件转化成彼此互斥的事件的和事件,再利用互斥事件的概率加法公式求解.(2)先求其对立事件的概率,再利用对立事件的概率公式求解.
3. 古典概率与统计的综合
例13. 某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表.
B地区用户满意度评分的频数分布表
(1)在图②中作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)根据用户满意度评分,将用户的满意度分为三个等级:
估计哪个地区用户的满意度等级为不满意的概率大?说明理由.
解析 (1)如图所示:
通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值;B地区用户满意度评分比较集中,而A地区用户满意度评分比较分散.
(2)A地区用户的满意度等级为不满意的概率大.
记CA表示事件:“A地区用户的满意度等级为不满意”;CB表示事件:“B地区用户的满意度等级为不满意”.
由直方图得P(CA)的估计值为(0.01+0.02+0.03)×10=0.6,
P(CB)的估计值为(0.005+0.02)×10=0.25.
所以A地区用户的满意度等级为不满意的概率大.
评注 有关古典概型与统计结合的题型是高考考查概率的一个重要题型,已成为高考考查的热点.概率与统计结合题,无论是直接描述还是利用频率分布表、频率分布直方图、茎叶图等给出信息,只需要能够从题中提炼出需要的信息,则此类问题即可解决.
六、几何概型
考纲要求
(1)了解随机数的意义,能运用模拟方法估计概率.
(2)了解几何概型的意义.
基本考点与题型
1. 与长度有关的几何概型
例14. 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )
答案 B.
解析 因为红灯持续时间为40秒.
所以这名行人至少需要等待15秒才出现绿灯的概率为=.
评注 对于几何概型的概率公式中的“测度”要有正确的认识,它只与大小有关,而与形状和位置无关,在解题时,要掌握“测度”为长度、面积、体积、角度等常见的几何概型的求解方法,本题的测度为长度,是高考中经常出现的一类几何概型送分题.
2. 与面积有关的几何概型
例15. 从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为( )
答案 C.
解析 利用几何概型,圆形的面积和正方形的面积比为==,所以π=.
评注 求解与面积有关的几何概型时,关键是弄清某事件对应的面积,必要时可根据题意构造两个变量,把变量看成点的坐标,找到全部试验结果构成的平面图形,以便求解.
3. 与其它知识交汇的几何概型
例16. 在区间[0,1]x+y≤上随机取两个数x,y,记p1为事件“x+y≤”的概率,p2为事件“xy≤”的概率,则( )
答案 D.
解析 如图,满足条件的x,y构成的点(x,y)在正方形OBCA内,其面积为1.事件“x+y≤”对应的图形为阴影△ODE,其面积为××=,故p1=<.
事件“xy≤”对应的图形为斜线表示部分,其面积显然大于,
故p2>,则p1<评注 与其它知识交汇的几何概型以测度为面积的居多,解决这类问题的关键是根据题意画出图形,并计算相关面积.这类问题综合性较强,有一定的难度.
变式训练
1. 某校三个年级共有24个班,学校为了了解同学们的心理状况,将每个班编号,依次为1到24,现用系统抽样方法,抽取4个班进行调查,若抽到的编号之和为48,则抽到的最小编号为( )
A. 2 B. 3 C. 4 D. 5
2. 已知甲,乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的m、n的比值=( )
8. 某单位为了了解用电量y(度)与当天平均气温x(℃)之间的关系,随机统计了某4天的当天平均气温与用电量(如下表),运用最小二乘法得线性回归方程为=-2x+a,则a=________.
9. 某次测量发现一组数据(xi,yi)具有较强的相关性,并计算得=x+1,其中数据(1,y1)因书写不清楚,只记得y1是[0,3]上的一个值,则该数据对应的残差的绝对值不大于1的概率为________.(残差=真实值-预测值)
10. 已知正方形ABCD的边长为2,H是边DA的中点. 在正方形ABCD内部随机取一点P,则满足|PH|<的概率为________.
11. 某网站针对“2016年法定节假日调休安排”展开的问卷调查,提出了A,B,C三种放假方案,调查结果如下:
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
12. 某校学生参加了“铅球”和“立定跳远”两个科目的体能测试,每个科目的成绩分为A,B,C,D,E五个等级,该校某班学生两科目测试成绩的数据统计如图所示,其中“铅球”科目的成绩为E的学生有8人.
(1)求该班学生中“立定跳远”科目的成绩为A的人数;
(2)已知该班学生中恰有2人的两科成绩等级均为A,在至少有一科成绩等级为A的学生中,随机抽取2人进行访谈,求这2人的两科成绩等级均为A的概率.
变式训练参考答案与解析
1. B. 2. D. 3. A. 4. C. 5. D. 6. C. 7. C. 8. 60. 9. . 10. +. 11. (1)n=40;(2). 12.(1)3;(2).
1. 系统抽样的抽取间隔为=6,设抽到的最小编号为x,则x+(6+x)+(12+x)+(18+x)=48,解得x=3.
2. 根据茎叶图,得乙组的中位数是33,甲组的中位数也是33,即m=3,又甲=(27+39+33)=33,所以乙=(20+n+32+34+38)=33,解得n=8,所以=.
3. 分数低于112分的人对应的频率/组距为0.09,分数不低于120分的人数对应的频率/组距为0.05,故其人数为×0.05=10人.
12.(1)因为“铅球”科目的成绩等级为E的学生有8人,所以该班有8÷0.2=40人,所以该班学生中“立定跳远”科目的成绩等级为A的人数为40×(1-0.375-0.375-0.15-0.025)=40×0.075=3.
(2)由题意可知,至少有一科成绩等级为A的有4人,其中恰有2人的两科成绩等级均为A,另2人只有一个科目成绩等级为A.
设这4人为甲、乙、丙、丁,其中甲、乙是两科成绩等级都是A的同学,则在至少有一科成绩等级为A的学生中,随机抽取2人进行访谈,基本事件空间为Ω={(甲,乙),(甲,丙),(甲,丁),(乙,丙),(乙,丁),(丙,丁)},一共有6个基本事件.
责任编辑 徐国坚
