立体几何
2016-05-30许少华
许少华


立体几何无论是客观性试题还是主观性试题都是以中档题或是中档偏下试题与考生见面,是我们主要得分之题.因此,我们说:它是我们必须坚守的阵地.当我们面对这一内容进行复习时,该如何进行呢?本文带你一起进入从基础知识、基本技能到常规方法与必备能力的全面复习与欣赏.
一、近三年全国(1)卷的考情报告与分析
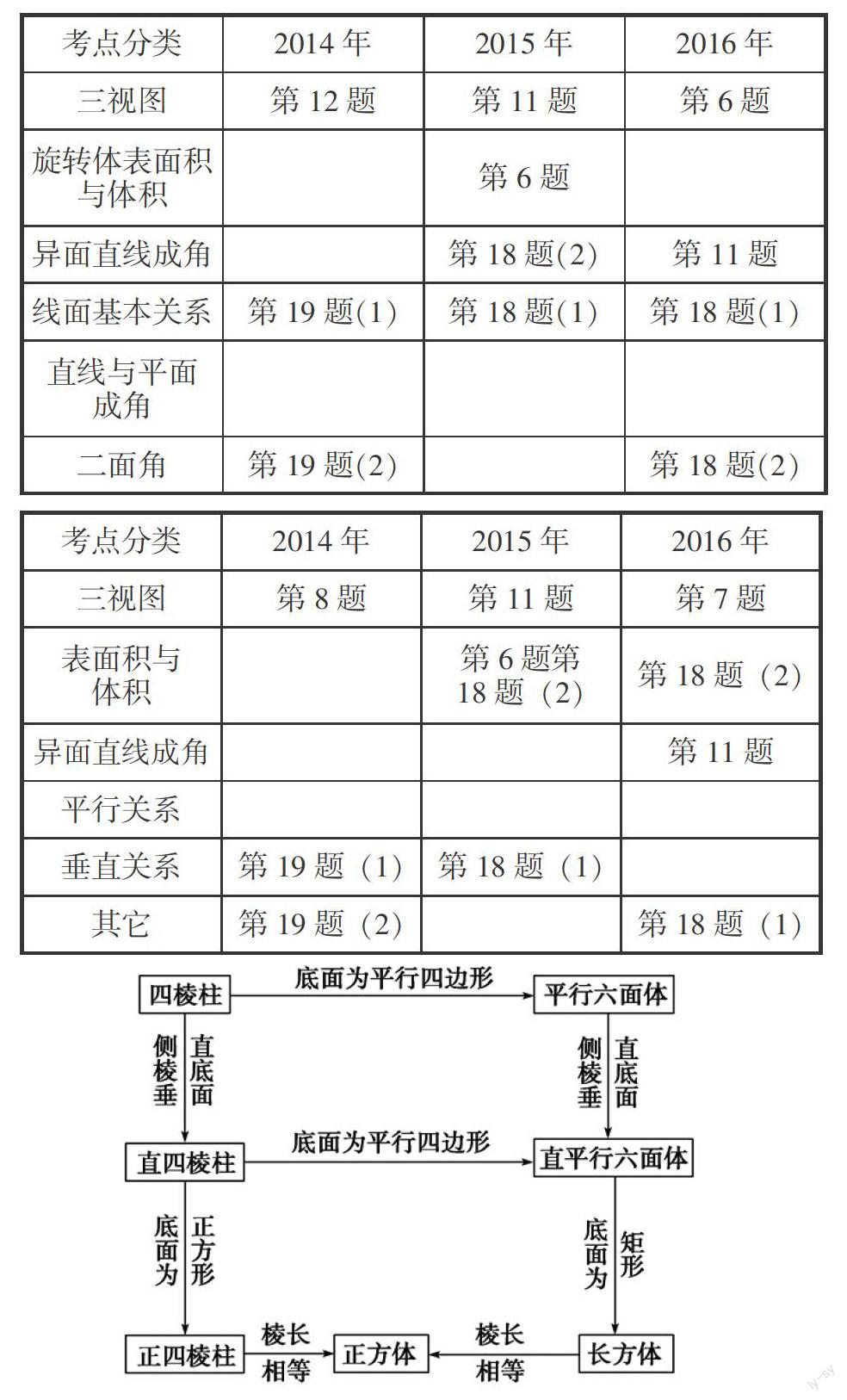
1.(1)理科试题分布情况
(2)文科试题分布情况
2. 考情分析
对于理科,由上表可以清晰的看出,三视图是年年都考,从试题的排位上可以看出,此类试题并不是最简单的题,多以中档题出现.旋转体的表面积与体积、线面位置关系、异面直线成角及二面角也是相对而言的高频考点.直线与平面所成的角也时常会在试卷中出现,复习时,不可过多强调,但绝不能不管不问,常规的处理方法必须掌握.
对于文科,由上表同样可以看出,三视图是年年都考,从试题的排位上也可以看出,此类试题同样不是最简单的题,也多以中档题出现.旋转体的表面积与体积、平行问题与垂直问题也是相对而言的高频考点.直线与平面所成的角及二面角虽然课本中有,但近年命题从未涉及,因此,复习这两个内容时,只达到了解层次即可.
二、基础知识整合
1. 空间几何体
1. 1. 必记概念与定理
(1)正棱锥的性质
侧棱相等,侧面是全等的等腰三角形,斜高相等;棱锥的高、斜高和斜高在底面内的射影构成一个直角三角形;棱锥的高、侧棱和侧棱在底面内的射影也构成一个直角三角形.
(2)四棱柱、直四棱柱、正四棱柱、正方体、平行六面体、直平行六面体、长方体之间的关系.
1. 2. 活用公式与结论
(1)常用面积和体积公式
①S圆柱侧=2πrl,S圆柱侧=πrl,S球=4πR2;
②V柱=Sh,V锥=Sh,V球=πR3.
(2)三视图排列规则:俯视图放在正(主)视图的下面,长度与正(主)视图一样;侧(左)视图放在正(主)视图的右面,高度和正(主)视图一样,宽度与俯视图一样.画三视图的基本要求:正(主)俯一样长,俯侧(左)一样宽,正(主)侧一样高.
1. 3. 辨明易错易混点
(1)应注意根据几何体的三视图确定几何体的形状和数量特征,尤其是侧视图中的数据与几何体中的数据之间的对应.
(2)弄清楚球的简单组合体中几何体度量之间的关系,如棱长为a的正方体的外接球的半径为a.
(3)搞清几何体的表面积与侧面积的区别,几何体的表面积是几何体的侧面积与所在底面面积之和,不能漏掉几何体的底面积.
2. 空间点、线、面的位置关系
2. 1. 必记概念与定理
(1)直线、平面平行的判定及其性质
① 线面平行的判定定理:a?α,b?α,a∥b?a∥α.
② 线面平行的性质定理:a∥α,a?β,α∩β=b?a∥b.
③ 面面平行的判定定理:a?β,b?β,a∩b=P,a∥α,b∥α?α∥β.
④面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b?a∥b.
(2)直线、平面垂直的判定及其性质
① 线面垂直的判定定理:m?α,n?α,m∩n=P,l⊥m,l⊥n?l⊥α.
② 线面垂直的性质定理:a⊥α,b⊥α?a∥b.
③ 面面垂直的判定定理:a?β,a⊥α?α⊥β.
④ 面面垂直的性质定理:α⊥β,α∩β=l,a?α,a⊥l? a⊥β.
2. 2. 活用公式与结论
(1)平行关系及垂直关系的转化
2. 3. 辨明易错易混点
(1)判定定理和性质定理中的条件不明确,导致判断出错.如由α⊥β,α∩β=l,m⊥l,易误得出m⊥β的结论,就是因为忽视面面垂直的性质定理中m?α的限制条件.
(2)明确图形的翻折与展开前后变与不变的量以及位置关系.对照前后图形,弄清楚变与不变的元素后,再立足于不变的元素的位置关系与数量关系去探求变化后的元素在空间中的位置与数量关系.
3.(理)空间向量与立体几何
3. 1. 必记概念与定理
线、面平行与垂直的向量方法
设直线l的方向向量分别为=(a1,b1,c1),平面α,β的法向量分别为=(a2,b2,c2),=(a3,b3,c3),则:
(1)线面平行:l∥α?⊥?·=0?a1a2+b1b2+c1c2=0.
(2)线面垂直:l⊥α?∥?=k?a1=ka2,b1=kb2,c1=kc2.
(3)面面平行:α∥β?∥?=λ?a2=λa3,b2=λb3,c2=λc3.
(4)面面垂直:α⊥β?⊥? ·=0?a2a3+b2b3+c2c3=0.
3. 2. 活用公式与结论
空间角的计算
(1)线线夹角
设l,m的夹角为θ(0≤θ≤),则cos θ==.
(2)线面夹角
设直线l与平面α的夹角为θ(0≤θ≤),则sin θ==│cos〈,〉│.
(3)面面夹角
设平面α、β的夹角为θ(0≤θ<π),则|cosθ|==│cos〈,〉│.
3. 3. 辨明易错易混点
(1)求二面角时,两法向量的夹角有可能是二面角的补角,要注意从图中分析.
(2)两条异面直线所成角的范围:0°<α≤90°;直线与平面所成角的范围:0°≤α≤90°;二面角的平面角的取值范围:0°≤α≤180°.
三、考点聚焦
1. 三视图
三视图是立几中的热点之一,每年高考都考,考题形式灵活多样,可能与画图结合,考查其中一个视图.可能与基本计算结合,考查其中一个视图的面积、几何体的最长边、表面的最大面积等.还可能与多面体的体积与表面积结合,考查表面积与体积的计算.
(1)识图
识图,既有对特殊几何体的识别,又有对几何体中截面形状的识别.围绕这一内容出现过一些典型试题,请看:
例1. 将正三棱柱截去三个角(如图1所示,A,B,C分别是△GHI三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
分析:首先要认识这个几何,注意图2几何体的特点,由于面AED垂直于底面EFD,于是,从侧面看过去,应该看到两个直角,从这点出发即可得到答案为A.
例2. 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为( )
分析:注意“长对正高平齐宽相等”,也就是说:正视图与俯视图的长要对正,正视图与侧视图的高要平齐,俯视图与侧视图的宽要相等.我们注意“正视图与侧视图的高要平齐”可排除A;再结合俯视图是正三角形,可知正视图,不可能是B与C,故正确选项为D.
(2)最值
例3. 某几何体的一条棱长为,在该几何体的正视图中,这条棱的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )
A. 2 B. 2 C. 4 D. 2
点评:本题的设计颇具特点,通过视图将线段与其投影联系在一起,然后再结合均值不等式产生结论,无论是哪一点不过关都不可能产生结果.
例4. 如右上图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
A. 6 B. 4
C. 6 D. 4
解析:该几何体是如图所示的棱长为4的正方体内的三棱锥E-CC1D1 (其中E为BB1的中点),
容易得到CC1=C1D1=4,C1D=4,EC=EC1=2,D1E==6.
其中,最长的棱为D1E=6.
例5. 一四面体的三视图如左图所示,则该四面体四个面中最大面的面积是( )
A. 2 B. 2
C. D. 2
解析:由三视图可得几何体如下图所示的棱长为2的正方体内的三棱锥B-CB1D1,结合图形,我们知道S△BCB1=×2×2=2, S△BB1D1= S△BCD1=×2×2=2,S△CB1D1==×2×2×=2.
比较可知,正确选项为D.
点评:例4与例5具有相似之处,都需要一一计算,然后进行比较产生结论.在计算过程中,首先要求由三视图转化为几何体必须准确;其次,要求对几何体的结构要十分清晰,构成该几何体的面与棱都准确掌握.否则,是极易出错的.
2. 表面积与体积
体积与表面积也是“小题”命题的热点之一,在此类试题的设计中往往与三视图结合,通过对三视图与几何体的转化产生几何体后,得到结论.
例6 .一个棱锥的三视图如图,则该棱锥的全面积(单位:cm2)为( )
(A)48+12
(B)48+24
(C)36+12
(D)36+24
解析:这是一个什么样的三棱锥呢?从俯视图中可以看出底面是等腰直角三角形,直角边长为6.再看俯视图中还有一条“斜边中线”,显然,它是一条棱的射影,那么,另外两条侧棱的射影在哪里?正好落在了斜边上,由此可知含这两条侧棱的侧面与底面垂直,且顶点在底面内的射影是底面直角三角形斜边的中点.
据棱锥的直观图,则有PO=4,OD=3,由勾股定理,得PD=5, AB=6,全面积为:×6×6+2××6×5+×6×4=48+12,故选A.
例7. 设某几何体的三视图如下(尺寸的长度单位为m). 则该几何体的体积为 m3.
解析:从俯视图与侧视图可以得到两个信息,一是顶点在底面上的射影位于底面三角形的一边上,且是底边上的四分之一分点;二是一个侧面与底面垂直;再看正视图,可以得到底面三角形的一个顶点在底边上的射影是该边的中点.
棱锥的直观图如上,这是一个三棱锥,高为2,底面三角形一边为4,这边上的高为3, 体积等于×2×4×3=4. 于是,该几何体的体积为4m3 .
例8. 如图,某几何体的三视图如下图所示,其中网格小正方形的边长为1,则该几何体的体积为( )
A. 8 B. 9
C. 10 D. 12
解析:由三视图可得几何体如图右图所示的三棱锥A-BCD,其中AB=AC=AD==2,底面三角形BCD中BD=4,CD=2且BD⊥CD,得S△BCD=×4×2=4.点A在面BCD内的正投影为BC中点,于是三棱锥A-BCD的高为h==
3.
故体积为V=×4×3=8.
3. 客观性试题的创新设计
立几中的客观性试题是立几试题改革与创新的“试验田”,近年出现了“百花齐放”的新景象,很多创新性的试题都在立几中出现.
例9. 如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是 .
解析一:作DO⊥AF于O并延长交AB于G,折起后AO⊥面DOG.当面ABD⊥平面ABC时,点D的投K影在哪里?其实,就是点G.
事实上,在面ABD内作DG′⊥AB于G′,则DG′⊥面ABC,从而DG′⊥AO,连OG′,得AO⊥面DOG′,于是G与G′重合.
设DF=x(1解析二:采用二个极端位置法,即对于F位于DC的中点时,t=1,随着F点到C点时,因CB⊥AB,CB⊥DK,∴ CB⊥平面ADB,即有CB⊥BD,对于CD=2,BC=1,∴BD=,又AD=1,AB=2,因此有AD⊥BD,则有t=,因此t的取值范围是(,1).
点评:本题的解析一很漂亮,分析出点D的投影K的具体位置是求解的关键,有了它,便有了一切;解析二抓住极端点的求解更漂亮,别具一格.它告诉我们对客观题的求解要灵活、不必追求循规蹈矩.
例10. 在正四棱柱ABCD-A1B1C1D1中,顶点B1到对角线BD1和到平面A1BCD1的距离分别为h和d,则下列命题中正确的是( )
A. 若侧棱的长小于底面的边长,则的取值范围为(0,1)
B. 若侧棱的长小于底面的边长,则的取值范围为(,)
C. 若侧棱的长大于底面的边长,则的取值范围为(,)
D. 若侧棱的长大于底面的边长,则的取值范围为(,+∞)
解析:设底面边长为1,侧棱长为λ(λ>0),过B1作B1H⊥BD1,B1G⊥A1B.在Rt△BB1D1中,B1D1=,B1D=,由三角形面积关系得h=B1H==. 设在正四棱柱中,由于BC⊥AB,BC⊥BB1,所以BC⊥平面AA1B1B,于是BC⊥B1G,所以B1G⊥平面AB1CD1,故B1G为点到平面A1BCD1的距离,在Rt△A1B1B中,又由三角形面积关系得d=B1G==.于是==·.
于是当λ>1,所以λ2+2>3,<1-<1,所以∈(,1).
例11. 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.设M是底面ABC内一点,定义
f(M)=(m,n,p),其中m,n,p分别是三棱锥M-PAB、 三棱锥M-PBC、三棱锥M-PCA的体积.若f(M) = (,x,y),且+≥8恒成立,则正实数a的最小值为_______.
解析:由题意得+x+y=××3×2×1=1?x+y=.
而+=+=2(1+a++)≥2(1+a+2)=2(1+)2,即+的最小值为2(1+)2,由于+≥8恒成立,则2(1+)2≥8?a≥1.
点评:本题打破了立几的常规命题模式,既“摆脱”了点、线、面,又依存于点、线、面,求解中一个巧妙地利用函数,一个适时地应用了基本等式,无论是求解还是将要面对的结论具有很大的创新性.
例12. 如图,一只小船以10 m/s的速度由南向北匀速驶过湖面,在离湖面高20 m的桥上,一辆汽车由西向东以20 m/s的速度前进.现在小船在桥下水平面P点以南的40 m处,汽车在桥上Q点以西30 m处(其中PQ⊥水面),则小船与汽车间的最短距离为 .
(不考虑汽车与小船本身的大小)
解析:设经过ts汽车在A点,船在B点,如下图,则有AQ=30–20t,BP=40–10t,PQ=20. 设点A在水平面的射影为C,连结CB,AB,不难得出△ACB 和△CPB 都是直角三角形,从而AB2=AC2+BC2=PQ2+PB2+PC2=202+(40–10t)2+(30–20t)2=100[5(t–2)2+9].
故当t=2时,线段AB最短,最短距离为30 m..
点评:面对此类问题,要记住“麻雀虽小,五脏俱全”;求解时一点也不能含糊,“实际问题”→“建立模型”→“产生数学结论”→“实际结果”的基本步骤一点也少不了.
4. 空间点、线、面的基本关系
立体几何涉及三种语言,图形语言、文字语言、符号语言,对于符号语言通常是通过选择题进行考查的,它要求对符号语言的准确理解与正确运用.
4.1. 基本关系
例13. α、β是两个平面,m、n是两条直线,有下列四个命题:
(1)如果m⊥n,m⊥α,n∥β,那么α⊥β.
(2)如果m⊥α,n∥α,那么m⊥n.
(3)如果α∥β,m?α,那么m∥β.
(4)如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
解析:对于命题(1)由于m⊥n,m⊥α,可得n在平面α内或n∥α,而n∥β,则平面α与平面β可能平行,于是,α⊥β是不正确的.
再看(2)由n∥α,则n必平行于α内某一直线n′,由于m⊥α,则m⊥n′,从而m⊥n. 显然,(2)是正确的.
命题(3)是两面平行的一个性质,虽然,课本中未直接给出,但我们讲课时都会说,没有难度.
命题(4)结合平行线的性质也容易产生结论.
点评:本题是一道填空题,它涉及四个命题正确性的判定.我们知道:从数学的严谨性角度看,肯定命题要给出证明,否定命题要举出反例. 显然,无论是证明还是举反例,对于一道填空来说是不易的,它要求必须对四个命题作出准确的判断,一个出错,“满盘皆输”,且此类题不需要四个命题都难度,只要有一个较难度就够了,显然,这不是“浅”考查的命题方式.它要求我们复习必须达到一定的深度.
4.2. 异面直线成角
例14. 直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为( )
A. B. C. D.
解析:如图,E为BC的中点. 由于M,N分别是A1B1,A1C1的中点,故MN∥B1C1且MN=B1C1,故MN∥BE,所以四边形MNEB为平行四边形,所以EN∥BM,所以直线AN,NE所成的角即为直线BM,AN所成的角.设BC=1,则B1M=B1A1=,所以MB===NE,AN=AE=,在△ANE中,根据余弦定理得cos∠ANE==.
点评:异面直线成角是近年高考命题的一个“小”热点,细心的人可能还记得2016年全国(1)卷文、理科的第11题给考生朋友带来的“惊喜”,那真叫考得“扎实”.
4.3. 线线平行、线面平行及面面平行
平行问题包括线线平行、线面平行及面面平行. 关于平行的判定与性质,内容十分丰富,设计试题的前景广阔,再加上各种距离或是各种面积与体积的计算,这一试题就非常好了.
例15. 如图,四棱锥中P-ABC,PA⊥平面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(I)证明MN∥平面PAB;
(II)求四面体N-BCM的体积.
解析:(1)由已知得AM=AD=2,取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.
又AD∥BC,故TN平行且等于AM,四边形AMNT为平行四边形,于是MN∥AT.
因为AT?平面PAB,MN?平面PAB,所以MN∥平面PAB
(Ⅱ)因为PA⊥平面ABCD,N为PC的中点,
所以N到平面ABCD的距离为PA.
取BC的中点E,连结AE. 由AB=AC=3得AE⊥BC,AE==.
由AM∥BC得M到BC的距离为,故S△BCM=×4×=2.
所以四面体N-BCM的体积VN-BCM=×S△BCM×=.
点评:本题建立在四棱锥的基础上进行设计,第一问证明线面平行,第二问求体积.无论是第一问还是第二问都是考查基本性质与基本方法的应用,只要我们掌握好常规的解题步骤就能顺利完成求解.
4.4. 线线垂直、线面垂直及面面垂直
垂直问题包括线线垂直、线面垂直及垂直平行.关于垂直的判定与性质,内容十分丰富,设计试题的前景广阔,同样再加上各种距离或是各种面积与体积的计算,这一类试题与平行问题相似也十分丰满.
例16. 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
(I)证明:AC⊥HD′;
(II)若AB=5,AC=6,AE=,OD′=2,求五棱锥D′-ABCEF体积.
解析:(I)由已知,得AC⊥BD,AD=CD.
又由AE=CF得=,故AC∥EF.
由此得EF⊥HD,EF⊥HD′,所以AC∥HD′.
(II)由EF∥AC得==.
由AB=5,AC=6得DO=BO==4. 所以OH=1,D′H=DH=3.
于是OD′2+OH2=(2)2+12=9=D′H2,故OD′⊥OH.
由(I)知AC⊥HD′,又AC⊥BD,BD∩HD′=H,
所以AC⊥平面BHD′,于是AC⊥OD′.
又由OD′⊥OH,AC∩OH=O,所以OD′⊥平面ABC.
又由=得EF=.
五边形ABCEF的面积S=×6×8-××3=.
所以五棱锥D′-ABCEF体积V=××2=.
点评:垂直问题的求解要抓住:线线垂直——线面垂直——面面垂直的基本思路.从基本图形入手,借助线线垂直的起点,产生我们需要的结论.
4.5. 平面的翻折
建立在某个图形的基础上,由部分图形沿一条特殊直线进行翻折产生空间问题,是立几命题的重要思路之一,此类试题的特点是,图形新颖、灵活,求解必须将新旧图形对照.
例17.如图(1),四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2,作如图(2)折叠,折痕EF∥DC.其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.
(1)证明:CF⊥平面MDF;
(2)求三棱锥M-CDE的体积.
点评:解决与折叠有关的问题的两个关键:(1)要明确折叠前后的变化量和不变量.一般情况下,线段的长度是不变量,而位置关系往往会发生变化.(2)在解决问题时,要比较折叠前后的图形,既要分析折叠后的图形,也要分析折叠前的图形.
5. 立体几何与空间向量
5.1. 直线与平面成角
直线与平面所成的角是空间角中的一种,它与线面垂直、线线垂直等联系相当密切,建
立在直线与平面基本关系的基础上设计直线与平面成角问题,用以全面考查立几的基础知识是完全可能的,因此,我们必须高度重视.
例18. 如图,四棱锥P-ABC中,PA⊥地面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(I)证明MN∥平面PAB;
(II)求直线AN与平面PMN所成角的正弦值.
解析:(I)由已知得AM=AD=2,取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.
又AD∥BC,故TN平行且等于AM,四边形AMNT为平行四边形,于是MN∥AT.
因为AT?平面PAB,MN?平面PAB,所以MN∥平面PAB.
5.2. 二面角
二面角是一个永不衰退的高考热点,近年命题较为频繁,面对此类试题我们的处理思路有两种:其一是通过“作——证——求”,运用立几的方法进行求解;其二是通过空间直角坐标系,利用空间向量完成求解.
例20. 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
(I)证明:平面ABEF⊥平面EFDC;
(II)求二面角E-BC-A的余弦值.
解析:(I)由已知可得AF⊥DF,AF⊥FE,所以AF⊥平面EFDC.
又AF?平面ABEF,故平面ABEF⊥平面EFDC.
(II)过D作DG⊥EF,垂足为G,由(I)知DG⊥平面ABEF.
以G为坐标原点,的方向为A轴正方向,
为单位长度,建立如图所示的空间直角坐标系G-xyz.
由(I)知∠DFE为二面角D-AF-E的平面角,故∠DFE=60°,则DF=2,DG=,可得A(1,4,0),B(-3,4,0),E(-3,0,0),D(0,0,).
由已知,AB∥EF,所以AB∥平面EFDC.
又平面ABCD∩平面EFDC=DC,故AB∥DC,CD∥EF.由BE∥AF,可得BE⊥平面EFDC,所以∠CEF为二面角C-BE-F的平面角,∠CEF=60°. 从而可得C(-2,0,).
故二面角E-BC-A的余弦值为-.
点评:本题第一问较简单,几乎是送分题.第二问要建立空间直角坐标系,为此我们要首先寻找三条两两垂直的直线,于是建立在第一问结论的基础上,很快找到了满足条件的三条直线,于是空间直角坐标系的三条轴也就找到了.
立体几何的常规命题是“两小一大”,分数为22分,占据部分近六分之一,但在最后你的得分中肯定超过六分之一,因此,当我们面对它时,我们说:这是必须坚守的阵地,无论如何都一定要保住它.
责任编辑 徐国坚
