小学数学符号意识的认识与思考

楚蓉

【摘要】 《数学课程标准（2011版）》10个核心概念词的提出是立足学生数学素养的形成和学生的发展，其本质上体现的是数学的基本思想：数学抽象、数学推理和数学模型思想. 数学思维的本质特点是抽象与推理，符号则是数学抽象最主要的语言表征，而运用符号进行数学思考是发展符号意识最具特色的思维方式，符号意识的培养及符号意识形成的过程又是数学模型的建立过程，同时也是一个数学化的过程.

【关键词】 符号意识；数学思想；数学建模

《课程标准（2011版）》指出“数学是研究数量关系和空间形式的科学”；“数学作为对客观现象抽象概括而逐渐形成的科学语言与工具，不仅是自然科学和技术科学的基础，而且在社会科学与人文科学中发挥着越来越大的作用”；“数学是人类文化的重要组成部分，数学素养是现代社会每一个公民所必备的基本素养”. 由此可以看出新修订的课程标准突出了数学课程的文化性和工具性，其中10个核心概念词的提出则是立足学生数学素养的形成和学生的发展上，其本质体现了数学的基本思想：抽象、推理、模型. 核心概念词之二的“符号意识”就是运用符号进行数学思考，这种思考就是数学基本思想的集中反映.

一、着眼于数学思想，理解符号意识的内涵.

首先，《课程标准（2011版）》将原来的“符号感”改为了“符号意识”，将“感”改为“意识”其意义与课程目标的价值取向和数学符号本质意义的要求更加吻合. 在数学学习中，无论是概念、命题学习还是问题解决，都涉及用符号表征数学对象，并用符号去进行运算、推理，得到一般性的结论. 数学的本质是概念和符号，并通过概念和符号进行运算和推理，用“意识”比用“感”更为准确. 可见，发展学生的“符号意识”是在培养和发展更高层次、更高水准的数学素养，更加强调学生主动理解和运用符号的心理倾向.

其次，新课标在表述中增加了“符号表示数”，可以理解为既可以用字母表示数，还包括用阿拉伯数学符号表示数. 这样看来，从孩童时代，孩子的符号意识已悄然开始，小时候玩的积木里就有了三角形、长方形、等图形符号；家长的启蒙教育大多从认识1、2、3等数字符号开始；从耳熟能详的儿歌“1像铅笔细又长，2像小鸭水中划——”这些数学符号经常被学生说在口头，用在笔端. 但是，学生们并不会将其上升到“符号”的意义. 如停留在这个基础上是远远不够的，这就需要教师在不断的唤醒中逐步培养学生的符号意识，体会数学的抽象，学会数学的推理和数学的建模，增强学生的符号意识.

二、立足教材编排，研究学生形成符号意识的思维过程

眼界决定境界，当我们用一种数学思考的眼光审视我们的教材时，就可以看到教材的编排者在“符号意识”方面的一些思考与设计，力图带着我们领会其背后的数学思想和独特的思维方式.

（一）

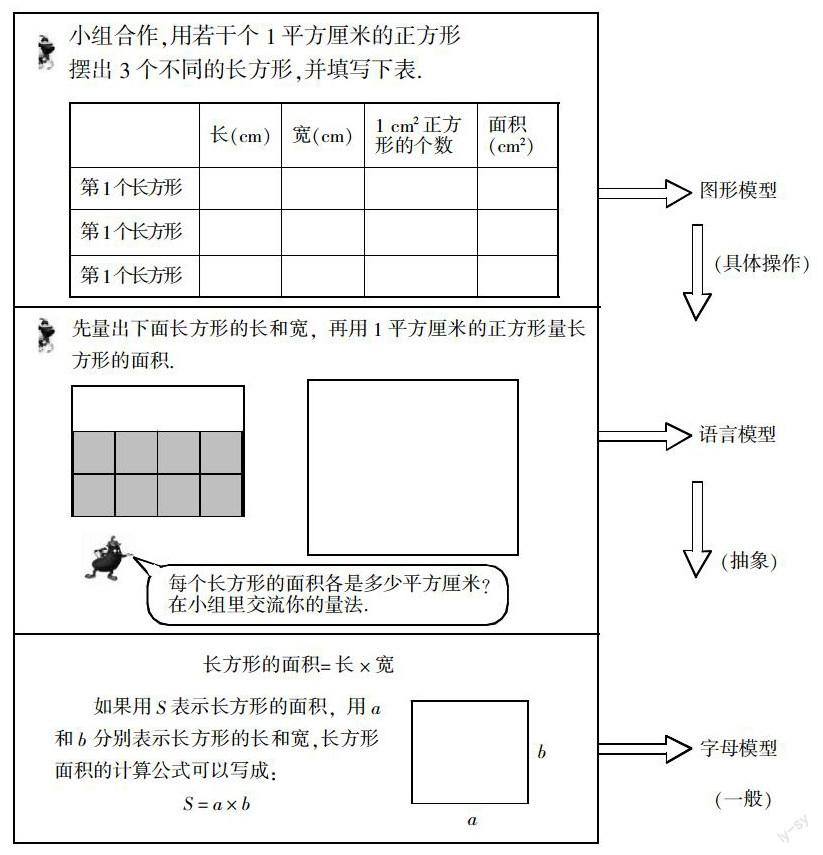
此内容的编排经历了从一个具体的情境中抽象出数量关系和变化规律，并用符号表示，这是一个从具体到抽象、从特殊到一般的探索和归纳的过程，借助直观的操作建立图形的模型，找到长方形面积和长与宽的数量关系并形成语言的模型，再抽象出字母模型，这不仅是一个数学建模的过程而且是符号意识形成的过程.

（二）理解符号所代表的数量关系和变化规律，这是一个从一般到特殊、从理论到实践的过程. 如假设一个正方形的边长是a，那么4a就是这个正方形的周长，a2就能表示为正方形的面积，这也是一个解释和应用模型过程，同时还是一个符号化的过程.

（三）纵看我们的九册教材. 在第一学段，学生接触更多的是简单的符号，这些符号如同象形文字，是那样的简明、形象、生动和传神. 如关系符号“=”，表示数学对象之间的关系. 它的首创者英国数学家列克尔德说“世界上再也没有比两条平行而又等长的线段意义更相同了. ”它不仅可以表示数与数、数与式的“等”还可以表示式与式的“等”，如此形象的等长就在学生感知“等”的过程中初步体会到了其背后的意义. 我们传达给学生的不仅是符号本身，更重要的是，从这些抽象的符号本身看到其所表征准确的数学意义，在不断唤醒中增强符号意识.

进入第二学段，学生的认知已经不只停留在符号的表面意义，他们已经能根据生活经验和学习经驗开始走进符号，去探寻符号背后更深的意义，不仅“懂”符号而且会“用”符号.

课标在第三学段中要求“能分析具体问题中的简单数量关系，并用代数式表示”，“通过用代数式、方程、不等式、函数等表达数量关系的过程，体会模型的思想，建立符号意识”.

数学的本质就是在不断的抽象、概括、模式化的过程中发展和丰富起来的.

研究数学问题的模式，可以表征为“抽象—符号—应用”，荷兰数学家弗赖登塔尔把这个过程称之为“数学化”. 不难看出，九册教材编排就是一个“数学化”的过程，就是在学生不断体会中建立模型的思想，建立符号意识的过程.

三、关注数学问题的解决过程，研究发展符号意识的有效策略

符号意识更多地表现为以学生为主体的一种主动用符号的意识，学生经历发现问题、提出问题、分析问题、解决问题的全过程，在这一过程中积累运用符号的数学活动经验，更好地感悟符号所蕴含的数学思想本质，逐步促进学生符号意识得到提高.

符号意识的形成过程就是建立符号模型的过程：

初步建立符号的模型. 从现实生活情境中，通过整理的信息，分析和描述问题的过程，经历一个从学生现有认知出发、不规范的数学语言通过规整和训练 走向严谨和标准语言，从而初步感受符号作用，抽象出数学问题.

二次建立符号模型. 抽象出来的数学问题，通过经验、对比再用符号表示，体会从特殊再到一般、从理论到实践的过程，再把得到的结论应用到实际生活中.

符号意识的建立过程就是一个数学化的过程，此过程旨在培养学生的分析、抽象、推理、简化等能力，引导学生用数学思考的眼光去体会数学的基本思想，在学习过程中抽象出符号，用符号发现规律并用形成的符号模型去解决实际问题，这样符号意识自然形成.

【参考文献】

[1]教育部.全日制义务教育数学课程标准（实验稿）[M].北京：北京师范大学出版社，2001.

[2]义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2011.

[3]义务教育数学课程标准（2011年版）解读[M].北京：北京师范大学出版社，2012.

[4]曹培英.跨越断层，走出误区：《数学课程标准》核心词的实践解读之二.小学数学教师[M].上海教育出版社，2013（11） .