数形结合思想在初中数学教学中的应用

李训超

摘 要：数形结合不应仅仅作为一种解题方法，而应作为一种十分重要的数学思想，它可以拓宽学生的解题思路，提高他们的解题能力。课堂教学中，我们要合理、灵活地应用数形结合的方法，展现数形结合的魅力，降低学生的学习难度，充分体现学生的主体性，从而激发学习兴趣，提高学习效率，发展智力与技能。本文主要介绍了数形结合方法在初中数学教学中的重要作用。

关键词：数形结合思想；数学教学；应用

中图分类号：G633.6 文献标识码：A 文章编号：1992-7711（2016）13-078-1

一、数形结合在初中数学教学中的地位与作用

初中数学研究的对象可分为两大部分，一部分是数，一部分是形，数与形是有联系的，这个联系就是数形结合。“数”与“形”反映了事物两个方面的属性。我认为，数形结合主要指的是数与形之间的一一对应关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”，即通过抽象思维与形象思维的结合，它可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的。数形结合在解题过程中应用十分广泛，如在解决集合问题，求函数的值域和最值问题，解方程和解不等式问题，三角函数问题，解决集合问题，解决平面几何与解析几何问题中都有体现，运用数形结合思想解题，不仅直观，易于寻找解题途径，而且能避免繁杂的计算和推理，简化解题过程。

二、数形结合思想在初中数字教学中的部分应用

1.在不等式方面的应用

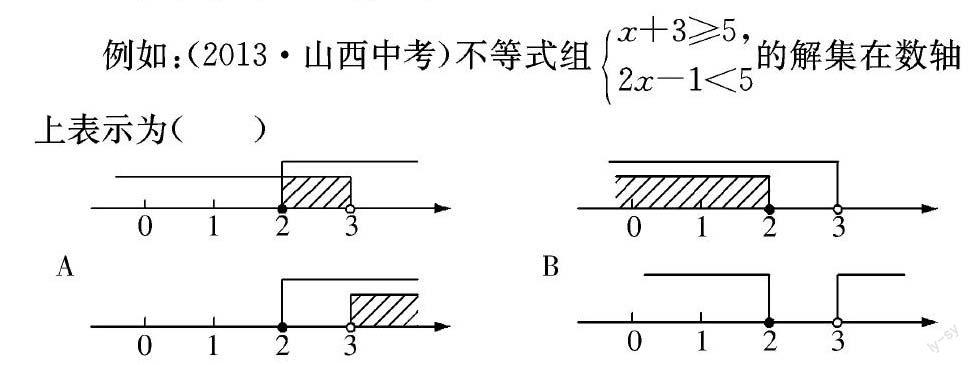
例如：（2013·山西中考）不等式组x+3≥5，2x-1<5的解集在数轴上表示为（ ）

教师在教学一元一次不等式（组）时，为了加深学生对不等式（组）解集的理解，教师要适时地把不等式的解集在数轴上直观地表示出来，使学生形象地看到，不等式有无限多个解。在数轴上表示数是数形结合思想方法的具体体现，而在数轴上表示数集，则比在数轴上表示数又前进了一步。确定一元一次不等式的解集时，利用数轴更为有效。

2.在方程方面的应用

处理方程问题时，把方程的根的问题看作函数图像的交点问题。

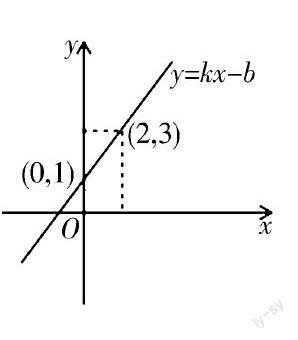
例如：一次函数y=kx+b（k，b为常数，且k≠0）的图象如图所示，根据图象信息可求得关于x的方程kx+b=0的解为x=-1。

本题考查了一次函数与一元一次方程，关键是根据函数的图象求出一次函数的图象与x轴的交点坐标，再利用交点坐标与方程的关系求方程的解，充分体现了数形结合的思想。

3.在函数方面的应用

利用图形的直观性来讨论函数的值域（或最值），求解变量的取值范围，运用数形结合思想考查和培养转化能力、逻辑思维能力，是函数教学中的一项重要内容。

例：若一次函数y=-2x+b的图象经过点A（2，2）。

（1）求b的值。

（2）在给定的直角坐标系中画出此函数的图象。

（3）观察此图象，直接写出当0本题考查函数图象经过点的意义，经过某点，说明点的坐标满足函数解析式；利用两点确定一条直线作一次函数图象简单方便。利用函数图像解决问题是数形结合的一种重要渠道。

4.在平面几何方面的应用

例1：如图，已知圆锥的底面半径为3，母线长为9，C为母线PB的中点，求从A点到C点在圆锥的侧面上的最短距离。

分析：最短距离的问题首先应转化为圆锥的侧面展开图的问题，转化为平面上两点间的距离问题。需先算出圆锥侧面展开图的扇形半径。看如何构成一个直角三角形，然后根据勾股定理进行计算。

5.在解析几何方面的应用

解析几何的基本思想就是数形结合，在解题中善于将数形结合的数学思想运用于对点、线、曲线的性质及其相互关系的研究中。

例：求过点A（0，6）且与C：x2+y2+10x+10y=0切于原点的圆的方程。

本题是一道几何问题，其几何量之间的关系运用代数式及圆方程来表示，并根据圆的方程的理论进行了由形到数的探究，充分体现了数形结合思想。

总之，在初中数学教学中要注重数形结合思想方法的培养，要充分研究与挖掘教材内容，将数形结合思想渗透于具体的数学问题中，在解决数学问题中让学生正确理解“数”与“形”的相对性，把它们有机地结合起来。当然，要掌握好数形结合的思想方法并能灵活运用，就要熟悉数学问题的图形背景，熟悉有关数学式中各参数的几何意义，培养结合图形思考问题的习惯，在学习中不断探索，积累经验，加强对数形结合思想方法的理解和运用。数形结合思想是一种很重要的方法，它贯穿于整个中学数学的教学课程。因此数形结合思想在中学数教学中起着举足轻重的作用，自觉运用它是提高数学能力的重要途径。