中国科举“五级百分”计量标准研究

黄裕泉 干有成 刘立云 赵霖

摘 要 群体考试成绩如何计量，时至今日仍属研究领域。美国大学入学考试、托福、GRE、雅思英语考试、中国国际汉语等级考试、中国大学招生考试、各级学校学生的学期考试等， 其计量标准和方法都不相同！中国国家计量法要求计量应建立国家统一标准，计量要有统一的计量单位和统一的计量基准、计量还必须有统一的监管 。我国古代 科举考试“五级百分”计量标准是古今中外最科学简便精准的计量标准。

关键词 计量单位 计量基准 计量原理 几何量数学模型

中图分类号：TB921 文献标识码：A DOI：10.16400/j.cnki.kjdkz.2016.06.012

1 计量单位（Unit of measurement）

单位制①的形成和发展与科技的进步、生产的发展密切相关；各种单位制的并存不仅对事物性质的界定有阻碍作用，而且也不利于民间科学文化的交流，因此，统一单位制已成为世界各国的共同要求。

我国古代传统的考试成绩计量单位，是实行的“五级、百分”计量单位制，简称为“五级百分制”。根据试卷答对题数的多少，每答对一题得一分，统计出的总得分数，即为考试成绩的“原始分”，再对照五级百分单位制，转换成统一的“五级百分”单位的“标准分”。据文献记载，五级分制起始于隋朝（公元607年），至今已有1500余年历史，后逐步发展成五级、百分制，即100分为最高分、60分为及格分，故有“60分万岁”的戏称，因为60分是及格的下限，不需要补考或重读而得名；60-70为及格、70-80为中等、80-90为良好、90-100为优等；五级、每一级10分，满10分晋升一级，从不及格到及格、从及格到中级、从中级到良级、从良级到最高优级，由量的积累变化（量变）而到质级的升级变化（质变），这是中国古代的一大发明。

2计量基准（criterion），泛指标准（Measurement standard）

基准按几何形式可分为：面基准、线基准、点基准。

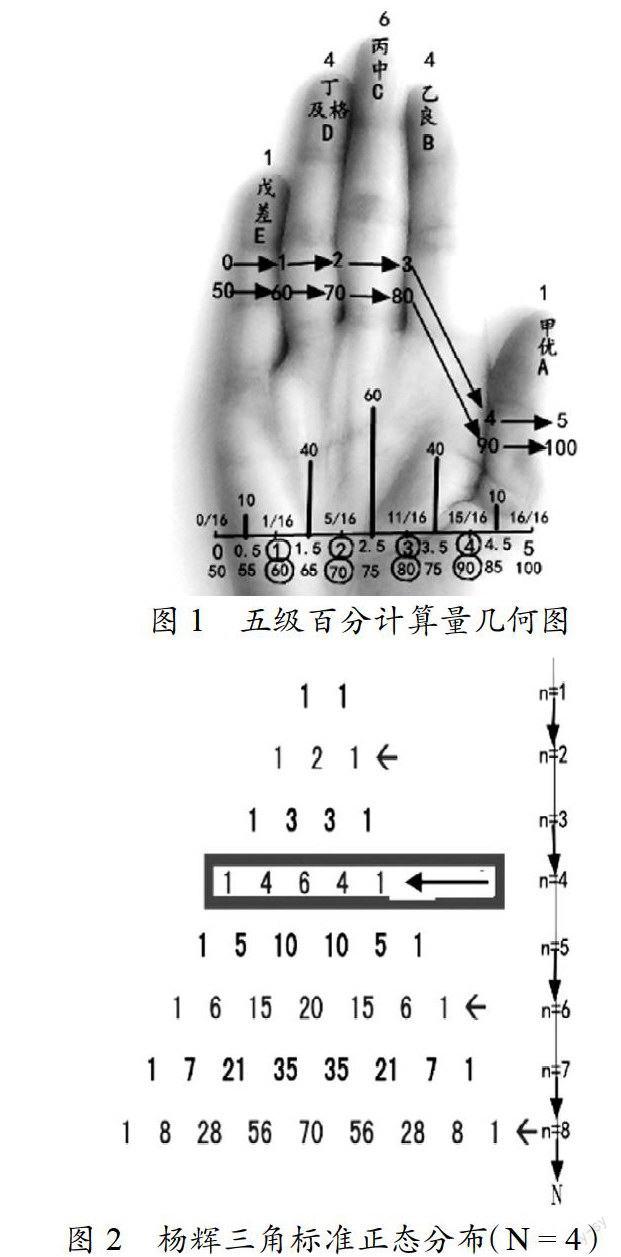
“五级百分制”量的界定，巧妙地利用人人都有的五个手指形体或手指面（界面），作为基准，用来表达群体考试成绩的五级；伸出大拇指为“优”、 伸出小拇指为“差”，其它三个手指依次为“良”、”中”、”及”格，俗称“五指计量”基准（图1）。这是我国古代了解认识群体智力水平的最朴素而形象、直观的一种表达方式。将五个手指数的自然数和量（0-1-2-3-4-5），定为计量基准。扩大10倍为（0～50），再将（0～50）变为（50～100），100分为群体中的最高分，60分为群体中的及格分，这是我国古代在群体考试成绩表达上的一大发明！这个发明每级为十进制，顶级为100分，巧妙地将正确率100%和名次序列第一名统一了起来。人的五个手指长短量不同，大致可分为三种类型，中指最长、大拇指和小拇指最短、食指和无名指次之。大拇指最短（数量最少），但是量最重（高），中指最长（数量最多），其量为中等，小拇指和大拇指对称数量最少，其量最轻（低）。

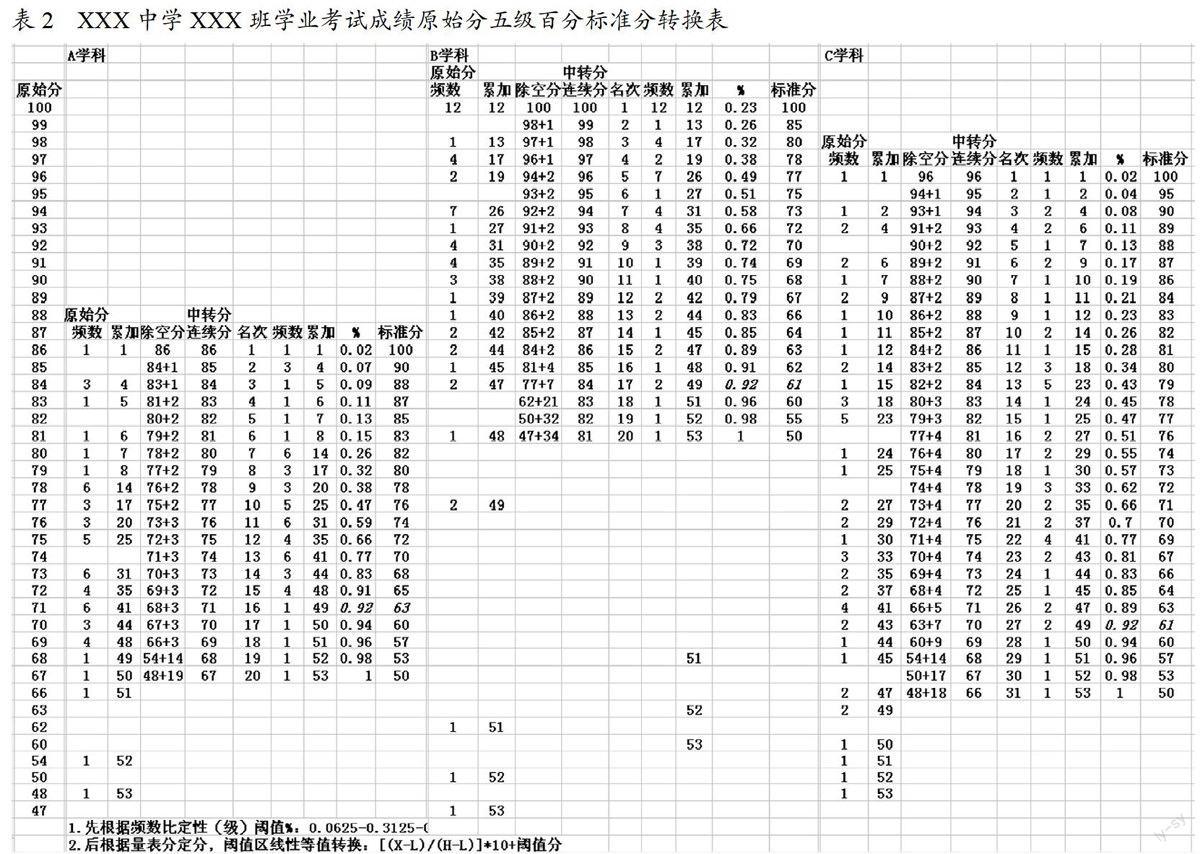
到了1262年我国数学家杨辉，在“详解九章算法中，用三角数表的形式展示出二项式展开的系数分布规律，即杨辉三角数表（图2）。手指的长度三种类型的比，可用标准正态分布频数的五级比（1：4：6：4：1）来表达，“优”级为（1/16）、良“级”为（4/16）“中级”为“6/16”、”及格”为“4/16”、“差级”为“1/16”）；分别对应于量表（1、2、3、4、5）。这就是杨辉三角标准正态分布，频数比（1：4：6：4：1）与对应的量表数（1、2、3、4、5）二者合一，就是群体考试成绩计量的基准（标准）（图3）。

3 计量原理和公式：（ Measurement principle and Statistical formula）

3.1 基准正态分布几何量数学模型（Mathematical model of geometric quantity）

几何量计量又称长度计量，是对各种物体的几何尺寸和几何形状的测量，以及为使几何量量值的准确和统一必须进行的计量工作。

群体考试的目的是“测量参与群体考试中每一个成员的考试成绩，在该群体的“基准正态分布几何量量表分上的定位和名次序列及百分位频数比序列上的定位”。由于考试的实施是通过考试试卷试题实现的，不同的试卷试题就是不同的考试标尺，考试成绩就会产生不同的分布幅度和不同的名次序列以及不同的频数分布，所以必须选择一个基准（标准）作为参照，进行标准正态分布基准转换的定位与定量，即将考试成绩的原始分转换为真正意义上的基准分即标准分。③

杨辉三角标准正态分布的五个频数比（1：4：6：4：1）和量表五个数（1、2、3、4、5）（图3），在不同的坐标上就会有不同的均数、中位数和众位数。在测量上首先要定“基准点-原点”，在计量上也即是“起点-原点”。将杨辉三角标准正态分布频数比和量表五个数置于“0”为起点的二维坐标上，量表五个数（1、2、3、4、5）就变成了量表五级分 “0-1-2-3-4-5”；频数16，以16个相同的长方块代表，按照频数累积就构成了正态分布塔型图，④这个塔型图就是标准正态分布几何量数学模型图（图3）。

3.2 标准正态分布几何量计算公式：纵轴频数/频数总数：（1、2、3、…16）/16

古代“两求斤”的16字口诀：“一退625（量表分1）、二125、三1875、四25、五3125（量表分2）、六375、七4375、八作5（量表分2.5）、九5625、十625、十一6875（量标分3）、十二75、十三8125、十四875、十五9375（量表分4）、十六为1（量表分1-5）”。该口诀起始于1262年我国宋代数学家杨辉的“日用算法”一书，完成于1299年我国元朝数学家朱世杰的“算学启蒙”。他将杨辉的八句口诀推进成完整的流传至今的16句口诀，它就是“个数位”的标准正态分布函数值。它同时也为“优、良、中、及格与不及格”五级分的界定，奠定了计量学的依据：“1/16为优、4/16为良、6/16为中、4/16为及格1/16为差”；累加百分率分别为，“6.25%以上的考试成绩原始分为优、31.25%以上为良、68.75%以上为中、93.75%以上为及格，以下的为差”。

分辨率提高一个数量级，即扩大10倍成“五十分位数”的标准正态分布函数值，分辨率提高两个数量级，即扩大100倍成“五百分位数”的标准正态分布函数值，以此类推（表1）。

因为（1：4：6：4：1），它是经过无限次的概率实验才能接近的概率极限值，即是概率的约定真值。依据“两求斤”16字口诀，计算出的函数值表

4 计量方法和程序：（Measurement methods and procedures）

4.1 依据基准频数比（1：4：6：4：1），实现定性（定级）转换

首先统计原始分成绩；然后将原始分从高分到低分依次排序；统计原始分的频数；⑤用频数/总数，得百分位；以原始分的最高分为起点，向下依次消除原始分中非连续分布的空白分，每消除一个空白分后续分依次增加一分，将非连续分布的原始分转换成连续分布的“中转分”；依据四个阈值点的百分位将群体分为五级（跨越6.25%以上的中转分定为D级、以下的定为E级；跨越31.25%以上低于68.75%以下的中转分为C级、跨越68.75%以上低于93.75%以下的中转分为B级、跨越93.75%以上的中转分为A级。因为是对称分布，所以反向亦然（图3）。

4.2 依据基准量表分，实现量表分定量（定分）六点等值转换

因为标准分每级为10分，六个等值点为（50、60、70、80、90、100）； A级最高分H=100、最低分L=90；B级最高分H=90、最低分L=80；C级最高分H=80、最低分L=70；D级最高分H=70、最低分L=60；E级最高分H=60、最低分L=50；将每级的原始分与每级的标准10分进行六点线性等值转换，其转换公式：

经过转换而成的五级百分标准分，三学科原始分的第一名都是100分，合法合情合理，因为是学校认可的考试，故是合法的，因为都是第一名所以是合情合理的；若以原始分划分，A学科第一名86分则属良级，这显然不合法不合情不合理；再从“优”级统计，A学科“优”级学生人数为“0”，而B学科“优”级生人数有38人，C学科“优”级生人数为7人，这显然也是不合法不合情不合理的！再以“良”级为例，以原始分划分，A学科“良”级以上的人数为8人，B学科为48人，C学科为24人。考试成绩不能以原始分划分等级不能以原始分报分，⑥这似乎在国际范围已成共识。以（1：4：6：4：1）的比例划分等级，这是极其简单而科学的方法，中国古代人的发明，可是现代人却把它遗忘了！另据新闻报道，2015年英国数学高考试卷太难，故原始分成绩太低，数以万计的学生在网上请冤，后来官方宣布原始分60分为A级，34分为及格；无独有偶，而2015年中国江苏小高考考试成绩原始分走向另一极端，4A人数暴涨！因为没有统一标准，所以混乱是必然会产生！

5 结论

通过杨辉三角基准正态分布数学模型（理论）和三学科原始分转换成的中国传统的五级分百分制的标准分实际应用证明，中国传统五级分百分单位制的量表（50～100）在各种类型的量表中，它是唯一的五级、百分、十进制自然数的单位制；基准量表五级分与基准频数五级比（1/16：4/16：6/16：4/16：1/16）固定的量数对应值；可以用每人的五个手指作为计量基准，就能将非正态分布的原始分，简便而准确地转换成中国传统的五级百分制标准分；因为它具有社会公用计量单位的基本属性，所以它能为“群体考试成绩社会公用计量的国家标准和国际标准提供科学依据。