找动滑轮支点的几种方法
2016-05-30施科桦
施科桦
摘 要:提高课堂教学的有效性,一直是受关注的问题,在教学过程中,为使学生对新知识更好地理解和接受,老师都是力求通过各种不同的方法来引导学生,而教学方法的不同,就会影响教学的有效性。动滑轮是省力杠杆,这个知识点是教学中的重点和难点,其中支点的位置是学生最为困惑。本文分析多种找动滑轮支点的教学方法,寻求提高课堂教学的有效性。
关键词:动滑轮支点;“圆盘”模型;直接给定法;实验法;台阶体验法
在《滑轮及其应用》这一节中,我们在讲动滑轮之前已先讲过了定滑轮,而且我们在讲定滑轮的时候利用杠杆的知识,教学生把圆看成是由无数根细棒——杠杆组成,这个学生很好理解,学生对于绕圆心转动的圆是非常熟悉的,比如:生活中的车轮,摩天轮等等,因此他们很容易接受定滑轮的固定点在圆心。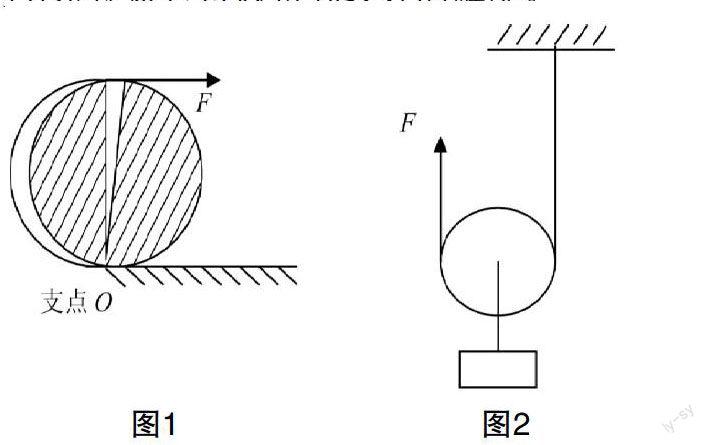
唯物辨证法告诉我们一切事物都存在着两个方面,这两个方面既相互对立又相互统一,要求我们坚持用一分为二的观点和全面的观点看问题。前面所提及的生活中的这些现象,对于理解定滑轮的固定点有很大的帮助,但从学习动滑轮来看,这些生活现象反而对动滑轮固定点的教学带来了阻力。因此动滑轮的支点在哪里学生就不好理解,为了突破这一难点,下面对几种教学方法进行分析。
1 “圆盘”模型
在“圆盘”模型中把动滑轮看成是一个放在地面上的圆盘,只要过圆的中心画一条圆的直径,一开始使这个圆的直径竖直在地面上与地面成90°角,在水平推力F的作用下,让这个圆盘在水平面上做一个微小的滚动,为使此现象明显,在这里我们可通过做一个PPT来演示,此时我们可以画出这个圆盘在地面上微小滚动时候的情境,如图1所示。
在讲解时引导学生观察图1中圆直径的微小转动,用圆直径的微小偏移来展示圆盘滚动时的支点O所在的地方。此时,提出一个问题“这个圆盘在地上滚起来,是以哪里为支撑?”或者可以这样问“哪一点可以支撑圆盘的滚动?”这时有些学生就会想到是圆盘与地面接触的地方,是圆盘转动支撑点,根据杠杆的定义,把圆的直径看成是一根硬棒,硬棒绕固定点转动时,该固定点即为圆转动时的支点。此时我们就顺势引出“这一点就是这个圆盘转动的支点”。然后把这个模型转移到动滑轮,让图1逆时针翻转90°成如图2动滑轮,引导学生把图2中右边竖直那条不动的绳看成是图1中的地面,此时滑轮沿着这条绳向上走,圆与这条绳接触的点就是该动滑轮的支点,在这里采用类比的方法使难点可以得到较好的解决。
这种教学方法不易操作的地方是需要学生进行抽象的思考,需要具备一定的空间思维和想象能力,其中圆的微小滚动转化成杠杆的微小转动,而杠杆的微小滚动是以哪里为固定点转动,比较抽象,空间思维和想象能力相对薄弱的同学对于该方法的学习会较困难。
2 直接给定法
根据滑轮的定义,绕一固定点转动的轮,那么在图3中的动滑轮,从整幅图来看,A点是固定不动的,在教学的过程中我们直接告诉学生:“可以把这个固定点A假设沿直线下移到O点,此时O点就是滑轮转动的支点”。
这个方法简便,学生接受起来也很容易,但学生是机械地记住老师告知他们的支点位置,实际上并没有真正的领悟到为什么O点就是动滑轮支点。
3 实验法
物理学是一门以实验为基础的科学,实验是解决物理问题的重要手段,我们物理学的发展是以实验为基础的,因此实验可以解决很多难点,而实验探究也是新课程改革倡导的教学理念,所以教科书设置了相应的实验探究环节,但教科书中并没有把实验表格列出来。
因此,在这里老师要引导学生设计相应的表格,如下表1:
在这个表格中只要测出两个量,一个是物重G,一个是拉力F,这里物重要比滑轮重大得比较多,从而减少系统误差。通过分析数据,比较物重G和拉力F的大小关系,可得出G=2F,在根据杠杆的平衡条件F1L1=F2L2可得出动力臂L1 =2L2,在根据力臂的定义:“支点到力的作用线的垂直距离”,来进行反推力臂的位置和支点的位置。
在图1中因为动力F这条力作用线正好是圆的切线,与切线垂直的线是过圆心的直线,从而再引导学生根据动力臂和阻力臂的比例分析可得出支点的位置O。
这种教学方法体现了物理的思想,实验法不仅是要了解它提供的实验结果,更重要的是要掌握实验的构思方法和研究物理问题的思路。这种方法充分体现了新课程学生学习方式,改变了死记硬背、机械练习的现状。学生主动参与、乐于探究、勤于动手、培养学生搜集信息和处理信息的能力、分析和解决问题的能力以及交流与合作的能力。教师在其中只起到了帮助、引导的作用。在概念与知识的形成过程中教师不是告之结论,而是在教师的帮助、引导下,由学生自主地去观察、发现、搜集信息、并用已有知识对所获信息进行归整。给学生提供了许多创造性思维的学习机会,突出学生作为课堂主体的地位,而教师将成为课堂学习的一员,师生共同探究,发现问题,探索新知。“把课堂还给学生”,让学生自主学习,自主思索,强调研究性学习,开阔了学生的思维,有利于学生的创新精神和实验能力的培养。但该方法存在的不足在于切线这个知识点属于数学知识,而数学切线这个知识点在初三才有学,所以在这里会对学生学习新知识有一个障碍。
4 台阶体验法
台阶法是以例题为切入点,创设一个情景,为学生形成新知识创造一个最近发展区,从而有利于学生接受新知识。
例:一个球在滚动的时候遇到一个台阶,为了使这个球滚上这个台阶,此时在一个球的上端添加一个水平作用力F,如图4(a)所示,问球是以哪一点为支点滚上台 阶的?
学生可以很容易地说是O点,在此再让学生体验一下O点的位置,此时我们运用体验,用一个篮球来做实验,把我们的手臂来代替台阶,让球滚过手,学生就会体会到球是绕手臂转动的,从而他们对支点O的位置更能体会并 接受。
我们根据原先的例题再进一步分析,接下来的分析要采用极值法。使这个台阶变小,此时这个支点O点就越来越靠近球的最底部,当这个台阶无限小的时候,支点O就是球与地面的接触点,如图3(b)所示。到这里学生都能理解,接下来采用类比法,把这个模型迁移到动滑轮,引导学生把图4(c)中右边竖直那条不动的绳看成是图4(b)中的地面,把自由端的力看成是例题中的水平推力F,让图4(b)逆时针翻转90°成如图4(c)动滑轮,此时滑轮沿着这条绳向上滚动,圆与这条绳接触的点就是该动滑轮的支点O。最后为了使学生回归到对杠杆知识的建立上,因为动滑轮它的实质是杠杆,所以还要是要运用无限等分思想把圆看成是由无数多根硬杆组成,再进行讲解。
在这里采用类比法和极值法使难点得到较好的解决。这样学生很容易就能够理解支点在哪里。极值法就是运用极限思维,使某些量的变化抽象成无限大或无限小去思考解决实际问题的一种解题方法。在初中物理解题过程中,有些题用一般的方法解比较繁琐,而用极值法常常能收到立竿见影、豁然开朗的效果。这种方法虽然没有太多的实验,由学生的体验再加上运用极值法通过抽象思维来解决问题,但这种方法教学也能使学生很好地掌握核心知识,而且能对于为什么O点是支点这个问题得到形象的理解。
上述讨论找动滑轮支点的多种教学方法,任何一种学习方式都有其独特的优势和不可避免的局限性,没有在任何情况下都是绝对优选的学习方式,因为还要根据学生的情况来确定教学方法。
