浅析数形结合方法在高中数学教学中的应用

徐婕

摘 要：高中数学是一门重要的基础学科，在高中数学中数形结合是分析解决问题的一项重要方法。学会数形结合方法不仅有助于学生对数学概念的理解，也有助于对其他科学问题的分析理解。在数形结合方法的具体应用中要注意遵循等价性原则、双向性原则和简洁性原则，教学实践中灵活地运用数形结合方法有助于学生对抽象概念的理解记忆，同时方便学生对于复杂问题的解答。

关键词：数形结合；高中数学；数学教学

中图分类号：G633.6文献标志码：A文章编号：2095-9214（2016）09-0057-01

一、引言

在高中课程的教育教学中，数学一直是教学的重点和难点。数学是一门重要的基础学科，几乎所有的现代学科都需要数学的支撑。同时数学也具有很强的抽象性和逻辑性，导致学生学习起来普遍感觉非常困难，多年来对高中数学教学方法的探讨一直是教育界的一个热门话题。数学是一门研究现实世界的数量和空间关系的学科，在数学方法中可以同时用图形和数字的方式对数学关系进行表达。数与形是数学体系中的两个重要的概念和工具，数形结合不仅是高中教学工作的重点，用好数形结合也是研究数学和其他科学问题的一个重要方法和途径。

数和形结合表达有利于学生对数学关系的理解，通过从不同的方面对事物进行研究可以互相借鉴，互相印证，更好地掌握数学关系的内在规律。通过将数量关系用图形来表示或者将图形关系用数量来表达，这样的研究方法就是数形结合的方法。数形结合可以将抽象的数学问题转变为形象具体的数量关系和图形关系，方便了对抽象事物的研究。數形结合是一种重要的研究方法和研究思想，掌握数形结合有助于提高学生分析问题的能力和解决问题的能力。

二、“数形结合”方法的应用原则

在教学实践过程中，科学地运用数学结合的方法可以简化问题的难度，提高学生的学习信心。由于数学学科很强的抽象性和逻辑性，导致相当一部分同学在学习中感到特别的吃力。将数形结合的方法应用到数学解题中有助于将抽象的问题具体化，激发学生的学习兴趣，同时还可以锻炼学生形象思维能力。数形结合的方法在具体的应用过程中只有遵循以下三个原则才能保证得到正确的结果[1]。

1.等价性原则。在数形结合过程中，用数和形两种不同的方式对同一个问题进行描述，两种不同方式相互转换过程中要主要符合等价的原则。在实践操作中，学生难以进行精确图形的绘制，因此主要用示意图的方式对图谱进行绘制。在绘图中要注意对关键节点和基本特征的描绘，避免因为构图偏差较大出现的解题失误。

2.双向性原则。在数形结合方法的运用过程中，既要对几何图形进行分析，还要对数据进行研究，通过二者的互相对应对图谱和数据进行修正。利用几何图谱的直观性克服数据的抽象性；利用数据的具体性和准确性克服几何图谱误差较大的缺点。充分发挥二者的各自优势，体现出数形结合方法的优势。

3.简洁性原则。在数形结合时要合理地构图，尽量确保图谱的简洁性，充分发挥几何图谱形象具体的优点。同时在代数计算中要尽量避免繁琐复杂的计算，降低解题的难度，达到化繁为简的目的。如果在构图的时候没有注意这一问题，随意构图往往会加大计算量，增加计算难度。在解题过程中浪费大量的精力和时间，甚至出现难以解答的现象。

三、“数形结合”方法在高中数学教学中的运用

数形结合是中学数学中常见的解题方法，在解题中灵活地进行数形结合有助于降低解题难度，直观地反应数据之间的相互关系。要想做到数形结合的科学应用，要准确掌握和理解各种数学关系之间的内在逻辑关系，熟悉各种数学运算用几何图形的表示方法。实现数、形的迅速转换，得到需要的结果和数据。

1.数形结合在对数学概念理解上的应用。高中数学中有许多抽象难懂的概念，直接记忆起来费时费力，而且效果较差。在实践中，学生可以通过数形结合的方法将这些抽象难懂的概念具体化，促进对一些抽象概念的理解和记忆。例如在高中数学中三角函数问题是一个重要的章节，里面出现了许多的概念和公式，例如正弦、余弦以及正弦余弦对应的二倍角公式等等。学生直接记忆起来感觉难度很大，但是如果引入数形结合的方法，通过画出正弦余弦的图谱，很容易就可以对他们的性质和公式进行掌握。例如学生将正弦sinx和余弦cosx的图谱分别画出来，就可以知道他们分别的奇偶性、周期及单调区间等性质，省去了大量的记忆时间[2]。

2.数形结合在抽象函数上的应用。在对抽象函数的解答上，很多学生都感觉非常的困难。尤其是一个选择填空题的解答中，如果用大量的计算进行分析解答的话势必会浪费宝贵的解题时间，造成后面大题解答时间不够。如果能够巧妙地将数形结合的方法应用到解题中去就可以很好地化繁为简，提高解题的效果。

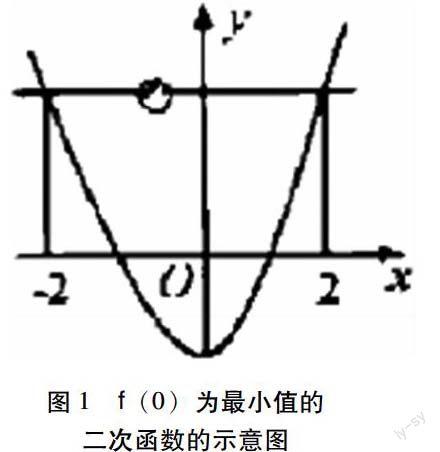
图1 f（0）为最小值的二次函数的示意图

例如如果一直f（x）为一个二次函数，且其在f（0）的时候取最小值。现已知f（a）四、结语

综上所述，高中数学的教学一直以来是中学教育界公认的难点，这是由数学学科高度的抽象性和逻辑性造成的。经过实践，将数形结合的方法应用到高中数学问题的解答中可以有效地降低数学问题的难度，提高学生的学习效率。在数形结合方法的具体应用上，要注意遵循等价性原则、双向性原则和简洁性原则。将数形结合方法科学灵活地应用到数学中去有助于学生对抽象概念和问题的理解记忆，同时有助于对复杂问题解答的简便化，提高学生的解题效率。

（作者单位：同升湖实验学校）

参考文献：

[1]常金明，王树香.浅析数形结合方法在高中数学教学中的应用[J].数学学习与研究：教研版，2015（7）：89-89

[2]董爱华.浅析高中数学教学中数形结合的应用策略[J].数学学习与研究：教研版，2015（21）：75-75