On 2-Adjacency Between Links∗

Zhixiong TAO

1 Introduction

Since the concept of n-adjacency(see[1,7])was introduced as a specialization of Gusarov’s notion of n-triviality(see[4])and a generalization of being unknotting number one(see[12,17],they coincide for n=1),a lot of research about n-adjacency of knots(in particular for n=2)has been done(see[1,8,18–21,23–24]).Furthermore,this concept can be naturally extended to 2-adjacency between two links(see[23–25]).That is,a link L is called 2-adjacent to a link W,if L admits a projection D containing two crossings c1,c2such that switching any 0＜ s≤ 2 of them yields a projection of W(see[1,18,23–24]).

In this paper,we are only concerned with 2-adjacency of two-component links.We study the relations between the signs of the crossings to realize 2-adjacency and the coefficients of the Conway polynomial of two related links.We give an expression of the Jones polynomial of the link obtained by opening two related crossings.We also study their Hom fl y polynomials and obtain some results and conditions on whether the trivial link is 2-adjacent to a nontrivial link,whether there are two links 2-adjacent to each other,etc.(see Sections 4–5).Finally,we show the Whitehead link not 2-adjacent to the trivial link,etc.,and give some examples to explain that for any given link,there are in finitely many links 2-adjacent to it.In particular,there are in finitely many links 2-adjacent to it,which have the same Conway polynomial.

Unless otherwise stated,throughout this paper,our convention will be the following:

Let a two-component link L=L1∪L2be 2-adjacent to W=W1∪W2,c1,c2the crossings to realize 2-adjacency,c1the crossing of L1,and α (resp. β)the sign of c1(resp.c2).Switching c1changes L1to W1,so L2=W2.

In this paper,we always assume a basic familiarity with Conway polynomial(defined by a skein relation,see[9,p.19]),the Jones polynomial(see[11,p.103]),Hom fl y polynomial(see[14])and their properties.The reader may refer to[3,9,11,13–14]for a more detailed exposition.

2 Conway Polynomial and 2-Adjacency of a Link

Proposition 2.1(see[5–6,9,15])Let L=L1∪ L2∪ ···∪ Lnbe an oriented link with n components,and ljk=lk(Lj,Lk)for jk.

(1) ∇(L)=zn−1(an−1+an+1z2+ ···+an−1+2mz2m);

(2)if n=1,then a0=1;if n=2,then a1=lk(L1,L2);if n=3,then

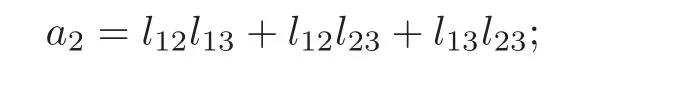
if n=4,then

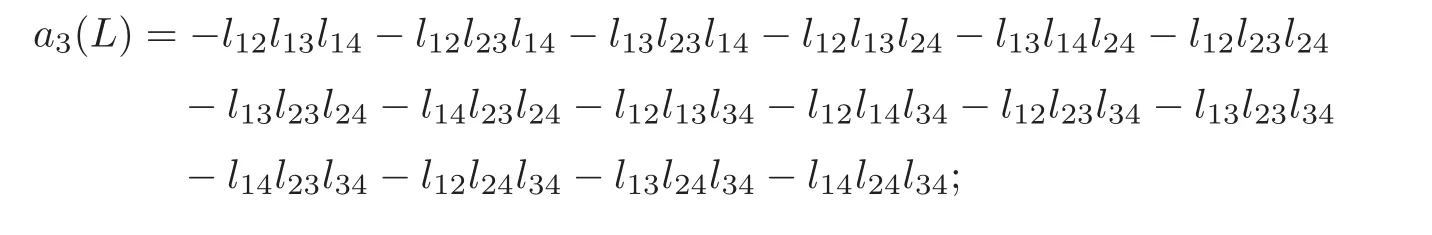
(3)if L+is an oriented knot and c is a positive crossing of L,then

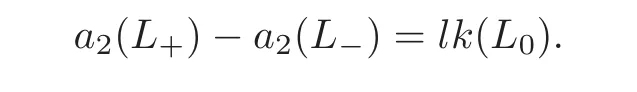
Here L−and L0are obtained by switching and opening c respectively,and aj(X)indicates the coefficient of zjin the Conway polynomial of a link X.

Moreover,lk(L)denotes the total linking number of L,i.e.,(see p.133 in[14]).

For the sake of convenience,let sx indicate switching crossing x,and ox opening x.According to the convention,L admits a diagram D(c1,c2),such that switching the non-empty subset of{c1,c2}yields a diagram of W respectively.By the definition(see[3,9,11])of Conway polynomial,we have

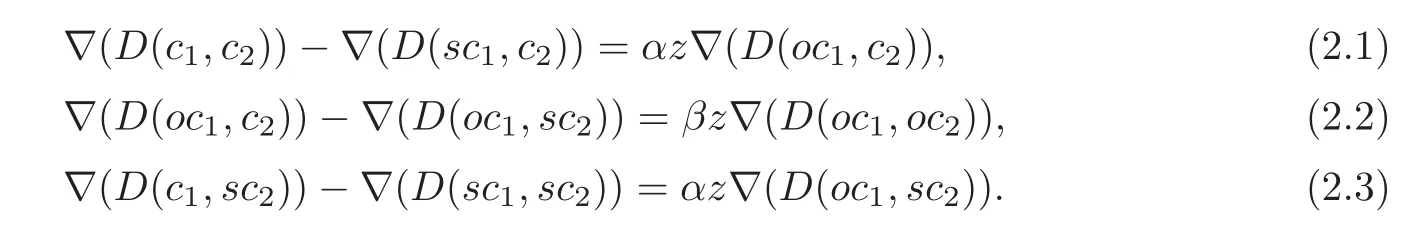
Here D(u,v)has the same diagram as D(c1,c2)except that u,v replace c1,c2respectively and α (resp.β)is the sign of c1(resp.c2)(see the above convention).Since D(sc1,c2),D(c1,sc2),D(sc1,sc2)are W,from the above equalities,we have

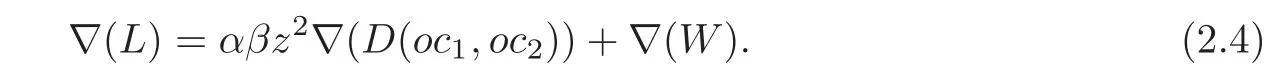
From the above argument and Proposition 2.1,we obtain the following theorem.

Theorem 2.1 If the notations and the conditions are as the convention,then lk(L)=lk(W)and

(1)if a3(L)a3(W),then D(oc1,oc2)is a two-component link;

(2)if a3(L)=a3(W),then either lk(L)=0 and D(oc1,oc2)is a link with two components or D(oc1,oc2)is a link with four components.

From Theorem 2.1,it is easy to see that c1and c2are not the crossings between two components,since lk(L)=lk(W).

In general,c1,c2have the following two cases.

Case 1 If c1,c2are the crossings of L1,then D(oc1,oc2)is a link with two or four components.

(a)If D(oc1,oc2)has two components,then lk(L)=lk(D(oc1,oc2)),and αβ can be got from a3(L)= αβlk(L)+a3(W).

However,if lk(L)=0,the identity does not determine αβ.In this case,we need to consider the following:(i)Switching c2changes L1to W2;(ii)switching c2(resp.c1)changes L1to W1and switching c1(resp.c2)changes W1to W2.For these two cases,we obtain W2=L2=W1.Hence,L1is 2-adjacent to W1.It is similar to(2.1)–(2.4)that we have

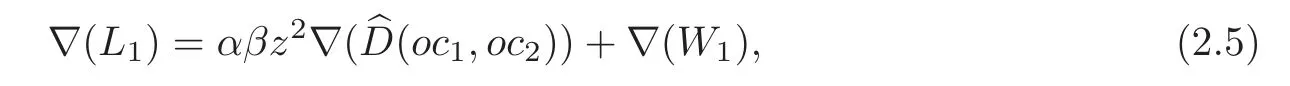
where(oc1,oc2)is obtained from L1by opening c1,c2and using Proposition 2.1.Thus,in both cases,αβ can be got from the identity a2(L1)=αβ+a2(W1).

(b)If D(oc1,oc2)has four components,then a3(L)=a3(W).

The discussion in(a)has shown that switching c2changes L1to W1and L1is 2-adjacent to W1.Moreover,using(2.5)and Proposition 2.1,we know that opening c1,c2changes L1to a three-component link,which is equivalent to a2(L1)=a2(W1).

Suppose that opening c1(resp.c2)changes L1to G1∪H(resp.G∪G3),and opening c2(resp.c1)changes H(resp.G)to G2∪G3(resp.G1∪G2).Denote L2and lk(Gj,Gk)by G4and ljk(1≤j＜k≤4)respectively.Since a2(L1)=a2(W1),then lk(G1∪H)=0 and lk(G ∪G3)=0,i.e.,l12= −l13=l23.In general,α,β can be determined by the identity a4(L1)−a4(W1)= −αβ(lk())2(see[21]),=(oc1,oc2)=G1∪G2∪G3and lk()=l12.

From the identity 0=a3(L)−a3(W)=αa2(G1∪H∪L2)and Proposition 2.1,we have

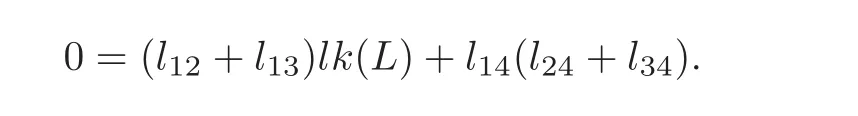
Similarly,0=(l13+l23)lk(L)+l34(l14+l24).

So l14(l24+l34)=0,l34(l14+l24)=0.

Notice that lk(L)=l14+l24+l34.If l24=0,then lk(L)=l14or lk(L)=l34.If l240,then lk(L)=l24(and l14=l34=0)or lk(L)=l34(=l14=−l24).Therefore,lk(L)is always equal to the linking number between L2and one of the other components of D(oc1,oc2)and lk(D(oc1,oc2))=l12+lk(L).

We see that if either L or W has a trivial linking number(e.g.the Whitehead link,etc.),theni.e.,a3(D(oc1,oc2))=0.In general,we have the following theorem.

Theorem 2.2 If the notations and the conditions are as the convention,c1,c2are the crossings of L1,and D(oc1,oc2)has four components,then

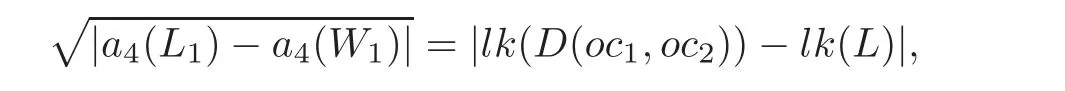
and a3(D(oc1,oc2))is(lk(D(oc1,oc2))−2lk(L))2lk(L)if all linking numbers of L2with any other component of D(oc1,oc2)are not zero,and is|a4(L1)−a4(W1)|lk(L)otherwise.

Proof Since l12=−l13=l23,by Proposition 2.1,a3(D(oc1,oc2))=lk(L)−2l12l14l34−l14l24l34.If l240 and lk(L)=l34=l14= −l24,since l12=lk(D(oc1,oc2))−lk(L),then a3(D(oc1,oc2))=[l212−2l12lk(L)+(lk(L))2]lk(L)=(lk(D(oc1,oc2))−2lk(L))2lk(L).The rest of the proof is obvious.

Case 2 If c1,c2are the crossings of the different components,i.e.,c1in L1and c2in L2,then D(oc1,oc2)is a four-component link.

It is similar to Case 1 to prove that after switching c2,although L2may become W1or W2,Ljis equal to Wj,j=1,2.

Now,let G1∪G2(resp.G3∪G4)be a link obtained from L1(resp.L2)by opening c1(resp.c2),and ljk=lk(Gj,Gk),1≤j＜k≤4,so lk(L)=l13+l14+l23+l24.From Proposition 2.1 and the identity 0=a3(L)−a3(W)= αa2(D(oc1,c2))= αa2(G1∪G2∪L2)= βa2(L1∪G3∪G4),we have

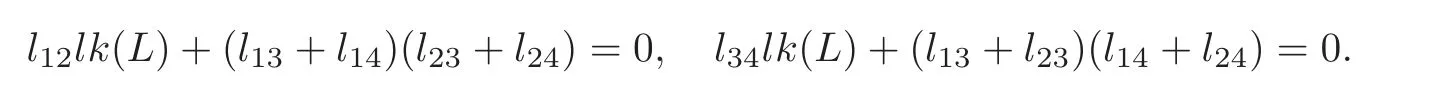
For the case of lk(L)=0(e.g.either L or W is the trivial link,the Whitehead link,etc.),by the above two equalities and lk(L)=l13+l14+l23+l24,we have l13=l14=l23=l24=0,so a3(D(oc1,oc2))=0.

Therefore,from the above discussion and Theorem 2.1,we obtain the following theorem.

Theorem 2.3 If the notations and the conditions are as the convention,lk(L)=0 and D(oc1,oc2)has four components,then a5(L)=a5(W).

3 Jones Polynomial and 2-Adjacency

Let V(X;t)indicate Jones polynomial(see[11])of link X.

Proposition 3.1(see[9,11,13])Suppose that V(G;t)is the Jones polynomial of a link G with c=c(G)components.

(1)If c(G)=1,then V′(G;1)=0,V′′(G;1)= −6a2(G).

(2)If c(G)＞ 1,then V′(G;1)= −3(−2)c(G)−2lk(G).

(3)V(G;1)=(−2)c(G)−1.

It is similar to the discussions of(2.1)–(2.4)that we have the following theorem.

Theorem 3.1 If the notations and the conditions are as the convention,then

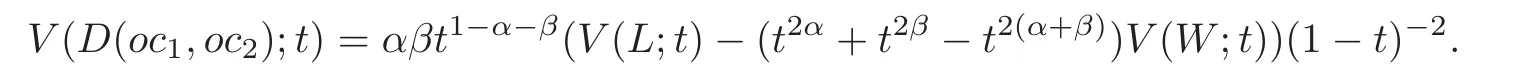
Corollary 3.1 The notations and the conditions are as the convention.D(oc1,oc2)is a link with four components if and only if a2(L1)=a2(W1);D(oc1,oc2)is a link with two components if and only if a2(L1)=αβ+a2(W1).

Proof According to Theorem 3.1,we have

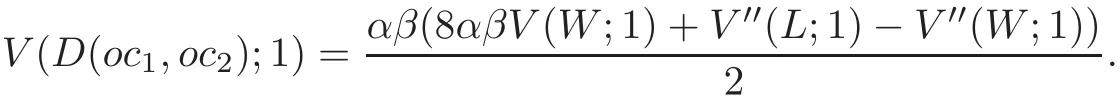
Since V(W;1)= −2,lk(L)=lk(W),a2(L2)=a2(W2),using corrected Murakami’s formula(see[16,22]),we have

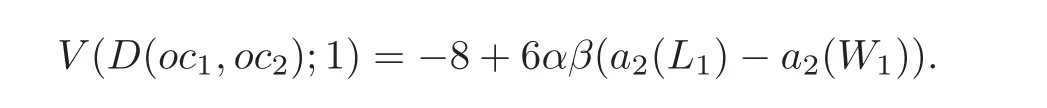
Thus,the results follows from Proposition 3.1.

4 Hom fl y Polynomial and 2-Adjacency

We use P(G)(l,m)=∑pj(l)mjto represent the Hom fl y polynomial(see[14])of a link G(sometimes we replace pj(l)by pj(G)or pj(G)(l)).i always denotes−1.Lickorish W.B.R.and Millett K.C.gave the following proposition.

Proposition 4.1(see[14]).Let link G have c(G)components and the other notations be as above.We have the following properties:

(1)If G is a link with c(G)≥2 components,then

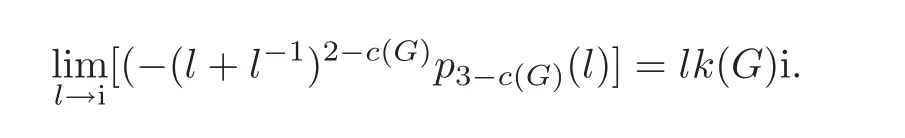
The exponent of the lowest power of m which appears in the Hom fl y polynomial of L is precisely 1−c(G).It has a coefficient

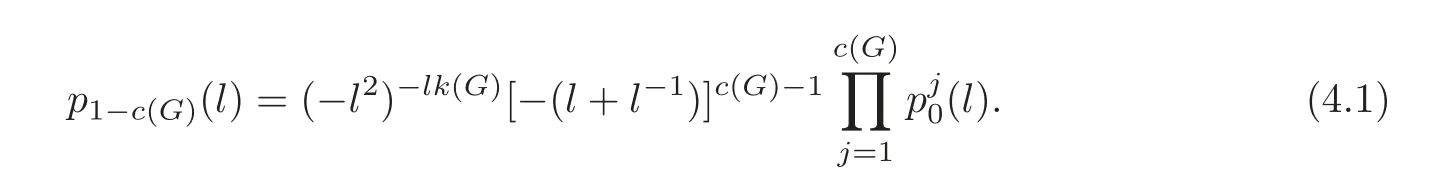
(2)If G is a knot,then

The notations and the conditions are as the convention.Then it is similar to the above argument in(2.1)–(2.4)that

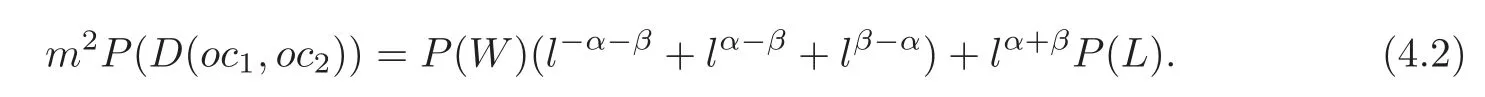
So we have the following theorem.

Theorem 4.1 If the notations and the conditions are as above,then

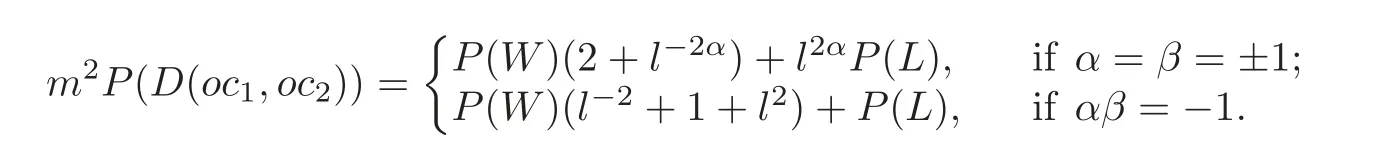
Furthermore,by Theorem 2.1 and(4.1),D(oc1,oc2)has two or four components depending on p−3(D(oc1,oc2))to be zero or not.So the following corollary is obtained easily.

Corollary 4.1 If the notations and the conditions are as above,and D(oc1,oc2)has two components,then

(1)α = β = ±1 ⇔ p−1(L)= −p−1(W)(l−4α+2l−2α);

(2)αβ = −1⇔ p−1(L)= −p−1(W)(l−2+1+l2).

Corollary 4.2 The notations and conditions are as the convention.

(1)If D(oc1,oc2)has two components,then p−1(L)(1)is an odd multiple of 6,or p0(1)of one component of L can be divisible by 3 and the other is trivial.

(2)If both components of L have trivial p0(l)(e.g.the trivial link,the Whitehead link,the Hopf link,etc.),then one component of W is the same as one of the components of L and the other has trivial a2.

Proof(1)It follows from(4.1)and the property that for any knot Q,p0(Q)(1)is an odd number.

(2)Assume a2(W1)0.From Corollary 3.1,we know that D(oc1,oc2)is a two-component link,i.e.,p−3(D(oc1,oc2))=0.Calculating p−1(L),by(4.1)–(4.2),we have

It is impossible.

Corollary 4.3 The notations and conditions are as the convention.If a3(L)a3(W),then 2-adjacency is one-way at most.

Proof Since a3(L)a3(W),by Theorem 2.1,D(oc1,oc2)is a two-component link.Furthermore,by Corollary 3.1,a2(L1)=αβ+a2(W1).

If W is also 2-adjacent to L,we can prove similarly that a2(W1)−a2(L1)=sign()sign(),where,are the crossings to realize 2-adjacency,W1is 2-adjacent to L1and D(o,o)has two components.Hence,sign()sign()= −αβ.

(1)If αβ =1,then by Corollary 4.1,p−1(L)= −p−1(W)(l−4α+2l−2α)and p−1(W)=−p−1(L)(l−2+1+l2),i.e.,

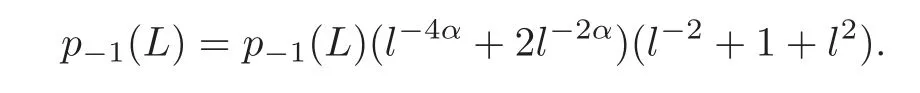
However,it is impossible.

(2)It is similar to prove the case of αβ = −1.

5 2-Adjacency of the Trivial Link

Corollary 5.1 The notations and the conditions are as the convention.If L is the trivial link and is 2-adjacent to W,then D(oc1,oc2)has four components.Furthermore,if a4(W1)=0,then lk(D(oc1,oc2))=0 and there exists an integer n such thatIn particular,if c1,c2are in the different components,then each component of D(oc1,oc2)has trivial p0(l).

ProofIf the trivial link is 2-adjacent to W,then according to Corollary 4.2,the trivial link can not be 2-adjacent to a link with a component whose a2is not zero.By Corollary 3.1,D(oc1,oc2)has four components.If c1,c2are in L1,then we know that L1is adjacent to W1.Since a4(W1)=0,by Theorem 2.2 and its proof,we obtain lk(D(oc1,oc2))=0 and all linking numbers between any two components of D(oc1,oc2)are zero.

If c1,c2are in different components,then W1,W2are trivial.By(4.1)–(4.2),

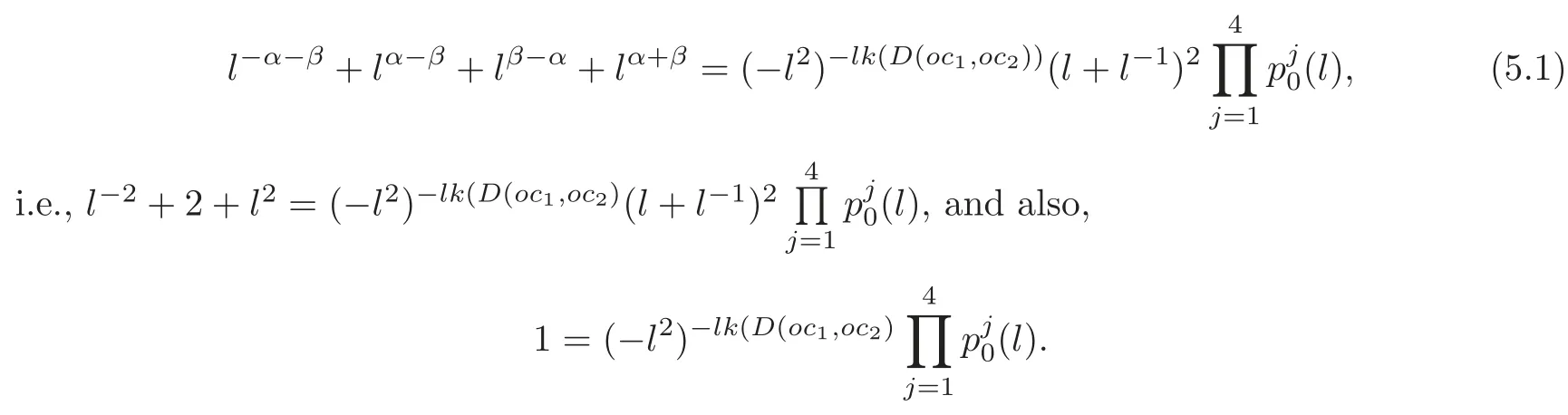
Hence,(l)=1,j=1,2,3,4,and lk(D(oc1,oc2))=0.

Next,taking l=1,by(4.1)–(4.2),we haveAssume

Furthermore,since(1)is always an odd number,the conclusion is true.

Corollary 5.2 Let the notations and the conditions be as the convention,L be the trivial link,c1,c2be the crossings of L1,a4(W1)=0 and D(oc1,oc2)have four components K1,K2,K3,K4(=L2=W2).Then

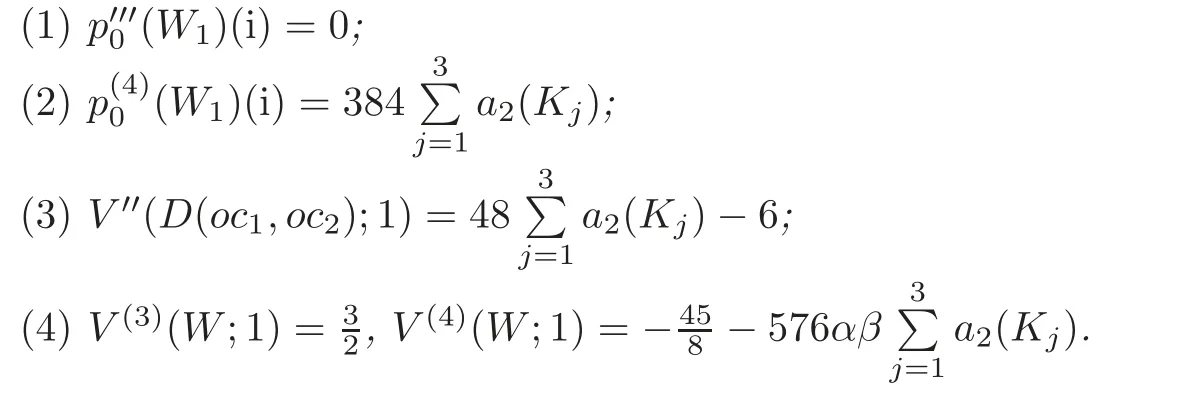
Proof From Corollary 5.1 and its proof,we know that lk(D(oc1,oc2))=0 and lk(Kj,Kk)=0,for any jk.Since L is the trivial link and D(oc1,oc2)has four components,by Corollary 3.1,a2(W1)=0,i.e.,and by(4.1)–(4.2),

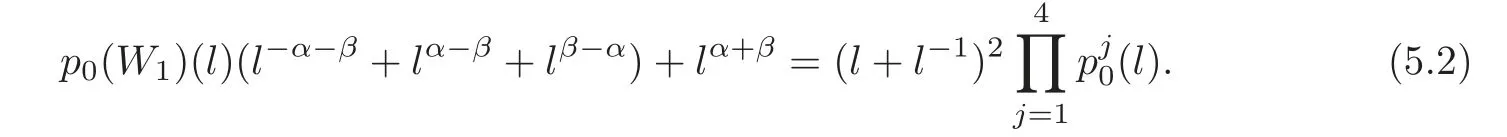
Thus,the result of(1)(resp.(2))is easily obtained by calculating the values of the third(resp.the fourth)derivatives of both sides of(5.2)atand by using Proposition 4.1.Using the corrected Murakami’s formula(see[16,22])and L’Hospital’s rule,we conclude with the result(3)–(4)can be obtained by calculating the values of V′(D(oc1,oc2);1),V′′(D(oc1,oc2);1)and by using(3),Proposition 3.1,L’Hospital’s rule and corrected Murakami’s formula again.

It is not difficult for the reader to find in finitely many two-component links,with one trivial component and the other nontrivial while a2=0.For instance,these links can be constructed by using 814,whose a2is zero.In fact,there are many knots like 814,such as 1033,1067,1082,10108,10116,10118,10146,etc.In[21],it has been proven that the trivial knot is not 2-adjacent to them.So by the proof of Corollary 5.1,the trivial link can not be 2-adjacent to the link constructed by the trivial knot and one of these knots.However,we do not know whether it is true in general.

6 Applications and Examples

Using the above results,we give two examples.

Example 6.1 The Whitehead link and the trivial link are not 2-adjacent to each other.

ProofWe consider whether the trivial link is 2-adjacent to the Whitehead link.Since theira3are not equal,by Theorem 2.1,D(oc1,oc2)is a two-component link.However,from Corollary 3.1,we know thatD(oc1,oc2)has four components.Hence,the trivial link is not 2-adjacent to the Whitehead link.

Similarly,we can prove that the Whitehead link is not 2-adjacent to the trivial link.

Example 6.2L7a2 andL7n1(see[2])are not 2-adjacent to each other.

Proof Choosing the directions of their components such that their linking numbers are 2.∇(L7a2)=3z3+2z,P(L7a2)=(l−9+3l−7+2l−5)m−1−(3l−7+4l−5−l−3)m+(2l−5−l−3)m3,∇(L7n1)=z5+4z3+2z,P(L7n1)=(l−9+3l−7+2l−5)m−1−(4l−7+6l−5)m+(l−7+5l−5)m3−l−5m5,∇(L7n1!)=z3+2z,P(L7n1!)=(2l−3+3l−1+l)m−1−(l−3+4l−1+l)m+l−1m3(hereL7n1!is the mirror image ofL7n1 and its linking number is−2).Using(4.1)–(4.2),we know thatD(oc1,oc2)is always a four-component link.However,theira3are different.By Theorem 2.1,L7a2 is not 2-adjacent toL7n1.

Similarly,we can prove thatL7n1 is not 2-adjacent toL7a2.

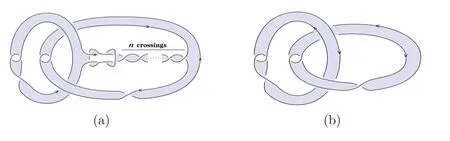
Figure 1 The links Lnand H

It is easy to check that the link in Figure 1(a)is 2-adjacent to the trivial link and for anyn∈N,its Conway polynomial is always zero.If the links in Figure 1 are denoted byLnandHrespectively,using the relation between bracket polynomial and Jones polynomial(see[10–11]),we have

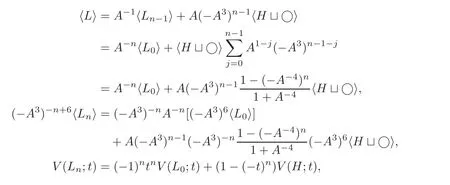
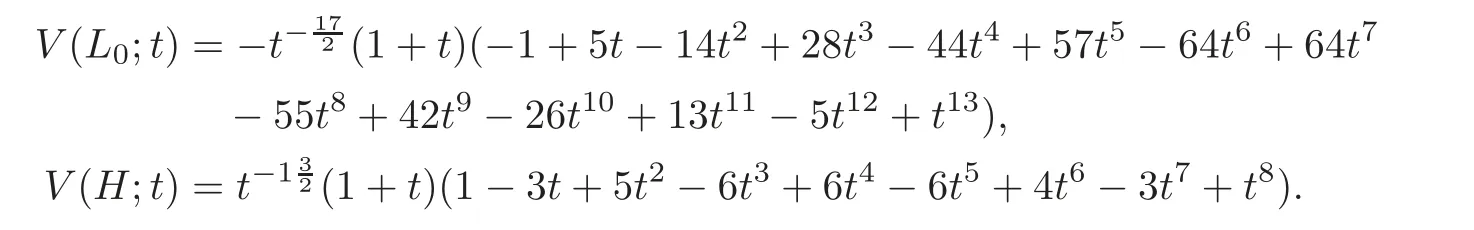
So,the highest-power term ofare different from each other.In other words,there exist in finitely many links 2-adjacent to the trivial link and their Conway polynomials are 0.

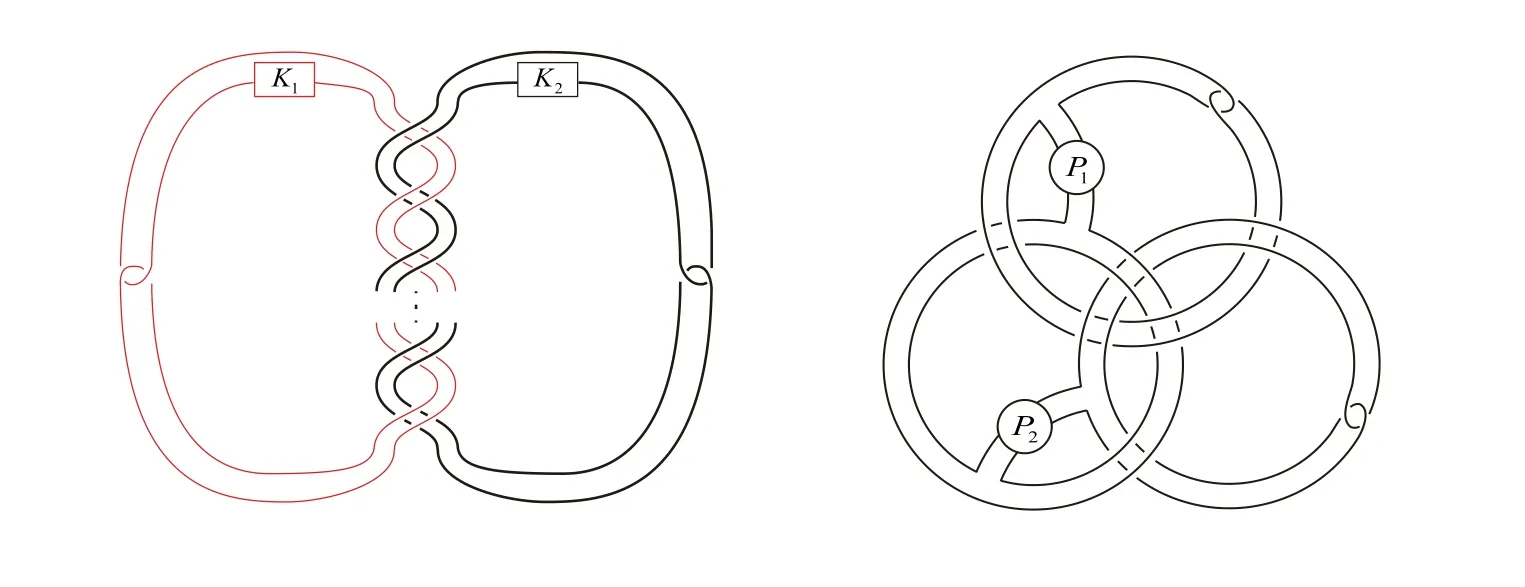
Figure 2 The two examples

The two examples in Figure 2 tell us that for any split link(such asK1∪K2andP1∪P2in Figure 2),we can find in finitely many links 2-adjacent to it.

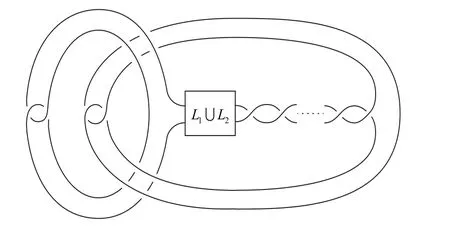
Figure 3 The links 2-adjacent to L1∪L2

Hereis a non-split link.Clearly,the example in Figure 3 shows the following fact that for any non-split link,we can find in finitely many links 2-adjacent to it,which have the same Conway polynomial andα,βcan be chosen as you want.

[1]Askitas,N.and Kalfagianni,E.,On knot adjacency,Topology and Its Applications,126,2002,63–81.

[2]Bar-Natan,D.,The Thistlethwaite link table,http://katlas.math.toronto.edu/wiki/The Thistlethwaite Link Table

[3]Burde,G.and Zieschang,H.,Knots,de Gruyter,Berlin,New York,1985.

[4]Gusarov,M.N.,Onn-equivalence of knots and invariants of finite degree,Advances in Soviet Math.,18,1994,173–192.

[5]Hoste,J.,The Arf invariant of a totally proper link,Topology and Its Applications,18,1984,163–177.

[6]Hoste,J.,The first coefficient of the Conway polynomial,Proceedings of A.M.S.,95(2),1985,299–302.

[7]Howards,H.and Luecke,J.,Strongly n-trivial knots,Bull.London Math.Soc.,34,2002,431–437.

[8]Kalfagianni,E.and Lin,X.S.,Knot adjacency,genus and essential tori,Pacific J.Math.,228(2),2006,251–275.

[9]Kauffman,L.H.,On Knots,Annals of Mathematics Studies,Vol.115,Princeton,University Press,Princeton,New Jersey,1987.

[10]Kauffman,L.H.,State models and the Jones polynomial,Topology,26,1987,395–497.

[11]Kawauchi,A.,A survey of knot theory,Birkh¨auser,Basel,Boston,Berlin,1996.

[12]Lickorish,W.B.R.,The unknotting number of a classical knot,Contemporary Mathematics,44,1985,117–119.

[13]Lickorish,W.B.R.and Millett,K.C.,Some evaluations of link polynomials,Commemt.Math.Helv.,61,1986,349–359.

[14]Lickorish,W.B.R.and Millett,K.C.,A polynomial invariant of oriented links,Topology,26(1),1987,107–141.

[15]Masbaum,G.and Vaintrobw,A.,A new matrix tree theorem,http://arxiv.org/pdf/math.CO/0109104.pdf[16]Murakami,H.,On derivatives of the Jones polynomial,Kobe J.Math.,3,1986,61–64,

[17]Scharlemann,M.,Unknotting number one knots are prime,Invent.Math.,82,1985,37–55.

[18]Stoimenow,A.,On unknotting numbers and knot trivadjacency,Mathematica Scandinavica,94(2),2004,227–248.

[19]Tao,Z.X.,On 2-adjacency of classical pretzel knots,Journal of Knot Theory and Its Ramifications,22(11),2013,1350066(13 pages).

[20]Tao,Z.X.,Conway polynomial of 2-adjacent knot,Journal of Zhejiang University,32(1),2005,17–20.

[21]Tao,Z.X.,2-Adjacency between knots,Journal of Knot Theory and Its Ramifications,24(11),2015,1550054.

[22]Tao,Z.X.,An Evaluation Property of Jones Polynomial of a Link,Journal of Zhejiang University,41(5),2014,509–511.

[23]Torisu,I.,On 2-adjacency relation of two-bridge knots and links,Journal of the Australian Mathematical Society,84(1),2008,139–144.

[24]Torisu,I.,On 2-adjacency Relation of Links,Proceedings of the International Workshop on Knot Theory for Scienti fi c Objects,2007,277–284.

[25]Tsutsumi,Y.,Strongly n-trivial links are boundary links,Tokyo J.Math.,30(2),2007,343–350.