Constructions of Metric(n+1)-Lie Algebras∗

Ruipu BAI Shuangshuang CHEN

1 Introduction

Lie algebras have played an extremely important role in physics for a long time.Their generalizations,known as n-Lie algebras(see[1–3]),also arise naturally in physics and have recently been studied in the context of M-branes(see[4–8]).The applications of n-Lie algebras to M-branes,quantization of Nambu mechanics,volume-preserving diffeomorphisms,integrable systems,and related generalizations of Lax equations have been considered in[9].

Due to the multiple multiplication,structures of n-Lie algebras are complex.Ling proved in[10]that there is only one finite dimensional simple n-Lie algebra over the complex numbers under the isomorphism,which is the(n+1)-dimensional n-Lie algebra g with dimg1=n+1.Kasymov in[11]defined nilpotent n-Lie algebras and Cartan subalgebras of n-Lie algebras,and proved that Cartan subalgebras of an n-Lie algebra are conjugate,and the similar Engel’s theorem is true in n-Lie algebras.More results on structures of n-Lie algebras can be seen in[12–17].A metric n-Lie algebra(L,[,···,],B)over a field F is an n-Lie algebra(L,[,···,])endowed with a non-degenerate symmetric bilinear form B:L⊗L→F satisfying the adinvariant Equation(2.2).The structure of metric 3-Lie algebras is applied to the study of the supersymmetry and gauge symmetry transformations of the world-volume theory of multiple coincident M2-branes(see[4]);the Bagger-Lambert theory has a novel local gauge symmetry which is based on a metric 3-Lie algebra(see[5,18]).Papers[19–20]studied structures of metric n-Lie algebras over the real numbers.Paper[21]discussed the isotropic ideals of metric n-Lie algebras over the complex numbers,and obtained the formulation on metric dimensions and numbers of minimal ideals of metric n-Lie algebras.

Realization of n-Lie algebras is very important,but it is indeed difficult.In reference[1],Fillipov constructed n-Lie algebras,called Jacobian algebras,by a commutative associative algebra A and n commutative derivations D1, ···,Dn,where the multiplication is defined as:For x1,···,xn∈ A,[x1,···,xn]=det(Di(xj)).Authors in[17,22–23]constructed some in finite dimensional simple Jacobian n-Lie algebras over the fields of positive characters.P.Ho,Y.Imamura and Y.Matsuo studied two derivations of the multiple D2 action from the multiple M2-brane model proposed by Bagger-Lambert and Gustavsson;they constructed metric 3-Lie algebras by arbitrary metric Lie algebras through 2-dimensional extensions(see[24]).Bai and collaborators realized 3-Lie algebras by Lie algebras,pre-Lie algebras,commutative associative algebras and linear functions and derivations(see[25–26]),and constructed(n+1)-Lie algebras by arbitrary n-Lie algebras(see[27]).They also constructed two-step nilpotent 3-Lie algebras by four index matrices(see[28]).In this paper we construct metric(n+1)-Lie algebras from metric n-Lie algebras(n≥2)and linear functions.

Throughout this paper,all n-Lie algebras(n≥2)are of finite dimension and over an algebraically closed field F of characteristic zero.Any bracket which is not listed in the multiplication of an n-Lie algebra is assumed to be zero.

2 Fundamental Notions

First we introduce some basic notions used in the paper(see[1,21]).An n-Lie algebra is a vector space g over a field F endowed with an n-ary multi-linear skew-symmetric operation[x1,···,xn]satisfying the n-Jacobi identity

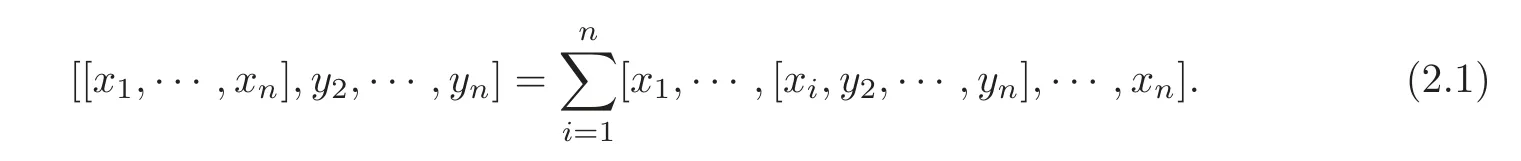
The mapping ad(x1,···,xn−1):g → g,ad(x1,···,xn−1)(xn)=[x1,···,xn]for all xn∈ g,is called a left multiplication defined by elements x1,···,xn−1∈ g.

A subspace I of g is called a subalgebra(an ideal)if[I,···,I]⊆ I([I,g,···,g]⊆ I).The subalgebra generated by the vectors[x1,···,xn]for all x1,···,xn∈ g is called the derived algebra of g,which is denoted by g1.If g1=0,then g is called abelian.If g10 and g has no ideals other than 0 and itself,then g is called a simple n-Lie algebra.A minimal(maximal)ideal is a nontrivial ideal I such that if J0 is an ideal of g andthen J=I(J=g).

The subset Z(g)={x ∈ g|[x,y1,···,yn−1]=0, ∀y1,···,yn−1∈ g}is called the center of g.Obviously,Z(g)is an abelian ideal of g.

Let(g,[,···,])be an n-Lie algebra.If a non-degenerate symmetric bilinear form Bg:g⊗g →F is ad-invariant,that is,for arbitrary x1,···,xn−1,y,z ∈ g,

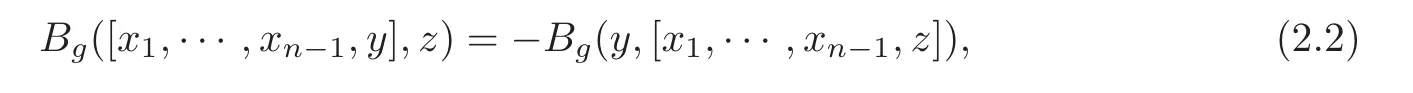
then(g,[,···,],Bg)is called a metric n-Lie algebra,and Bgis called a metric on g.For a subspace W of g,the orthogonal complement of W is defined by

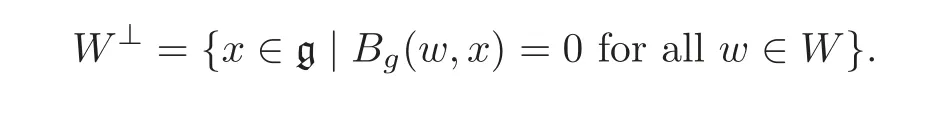
If W is an ideal,so is W⊥and(W⊥)⊥=W.Notice that W is a minimal ideal if and only if W⊥is maximal.We say that W is isotropic(coisotropic)if W ⊆W⊥(W⊥⊆W).It is not difficult to see that g1=[g,···,g]=Z(g)⊥.

Lemma 2.1(see[27])Let(g,[,···,],Bg)be an m-dimensional metric n-Lie algebra with a basis{x1,···,xm}.Suppose that x−1and x0are not contained in g.Set

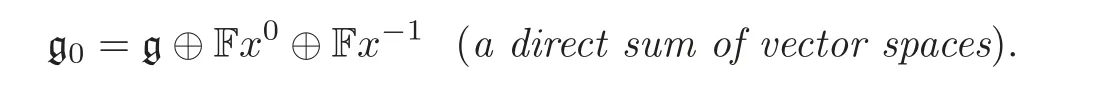
Then(g0,[,···,]0,B0)is a metric(n+1)-Lie algebra whose bracket and metric are given below.For every 1≤k≤n+1,

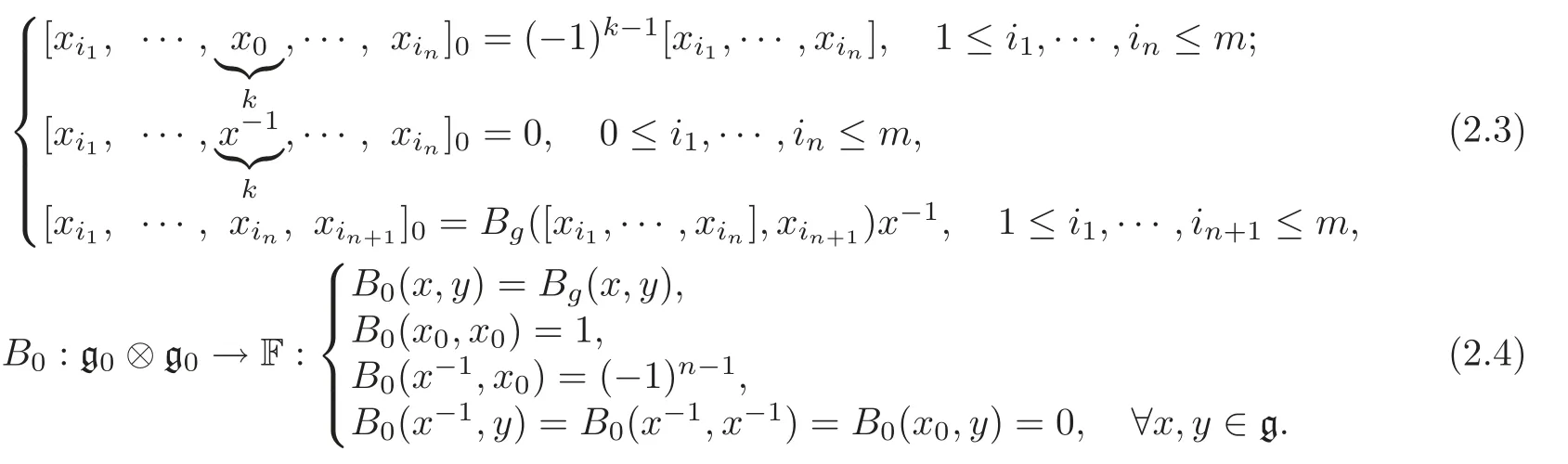
Lemma 2.2(see[25])Let(g,[,···,])be an n-Lie algebra and f ∈ g∗the dual space of g.If f0 and f(g1)=0,then(g,[,···,]f)is an(n+1)-Lie algebra,where[,···,]fis defined as follows:for all x1,···,xn+1∈ g,

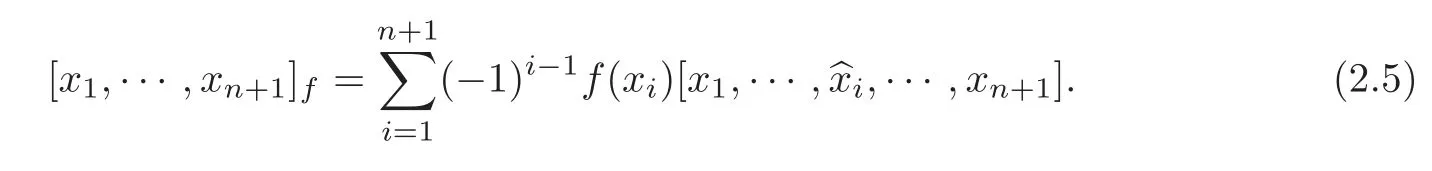
3 One Dimensional Extensions of Metric n-Lie Algebras

Let(g,[,···,],Bg)be an m-dimensional metric n-Lie algebra.If f ∈ g∗and f(g1)=0,we construct(m+1)-dimensional(n+1)-Lie algebras.

Theorem 3.1 Let(g,[,···,],Bg)be a non-abelian metric n-Lie algebra.If 0f ∈ g∗and f(g1)=0,then Bgis not ad-invariant on the(n+1)-Lie algebra(g,[,···,]f),where[,···,]fis defined as Equation(2.5).

Proof If for all x1,···,xn,y,z ∈ g,Bgsatisfies Bg([x1,···,xn,y]f,z)+Bg(z,[x1,···,xn,z]f)=0,then by Equation(2.5)

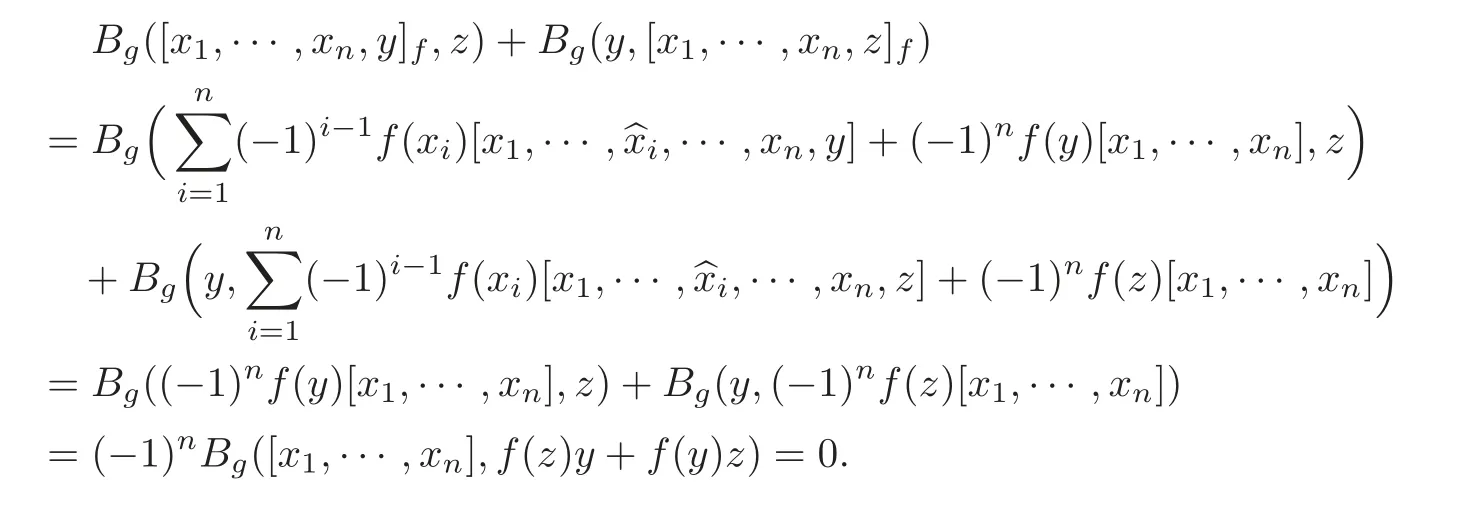
Since f0,there is a basis{v1,···,vm}of g such that f(v1)=1 and f(vi)=0 for 2 ≤ i≤ m.It follows that v1/∈g1and

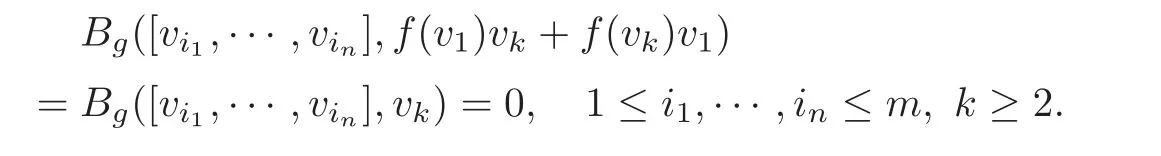
Since Bg([vi1,···,vin],v1)= −Bg(vin,[vi1,···,vin−1,v1])=0,Bg(g1,g)=0.Therefore,g1=0,a contradiction.The desired result follows.

Theorem 3.2 Let(g,[,···,],Bg)be a metric n-Lie algebra and g1g.Suppose that c is an element not in g,and suppose that L=g˙+Fc is the one-dimensional extension of the vector space g.Then there is a nonzero f ∈ g∗such that f(g1)=0 and(L,[,···,]cf)is an(n+1)-Lie algebra,where the multiplication[,···,]cfis defined as follows:

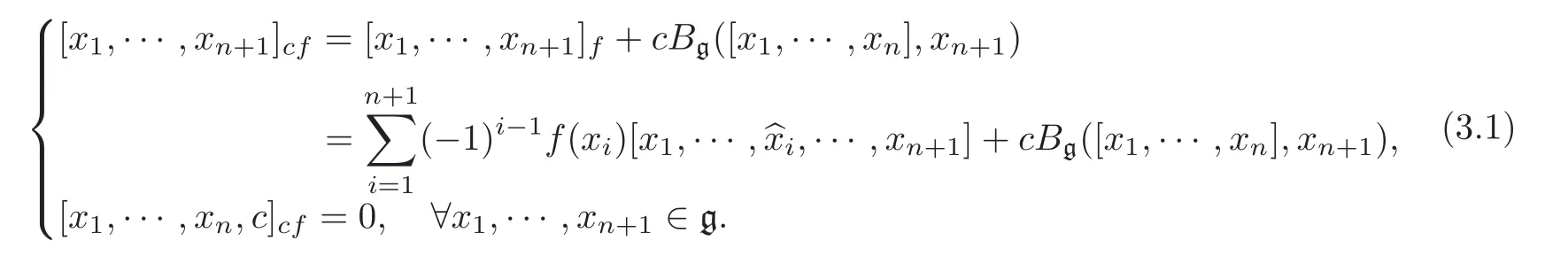
Furthermore,if the center Z(g)is non-isotropic,then there is a metric B on(L,[,···,]cf)such that B(v,w)=Bg(v,w)for all v,w∈g.

Proof By Equations(2.2)and(2.5),we only need to prove that[,···,]cfsatisfies Equation(2.1).For all x1,···,x2n+1∈ g,by Equation(3.1),

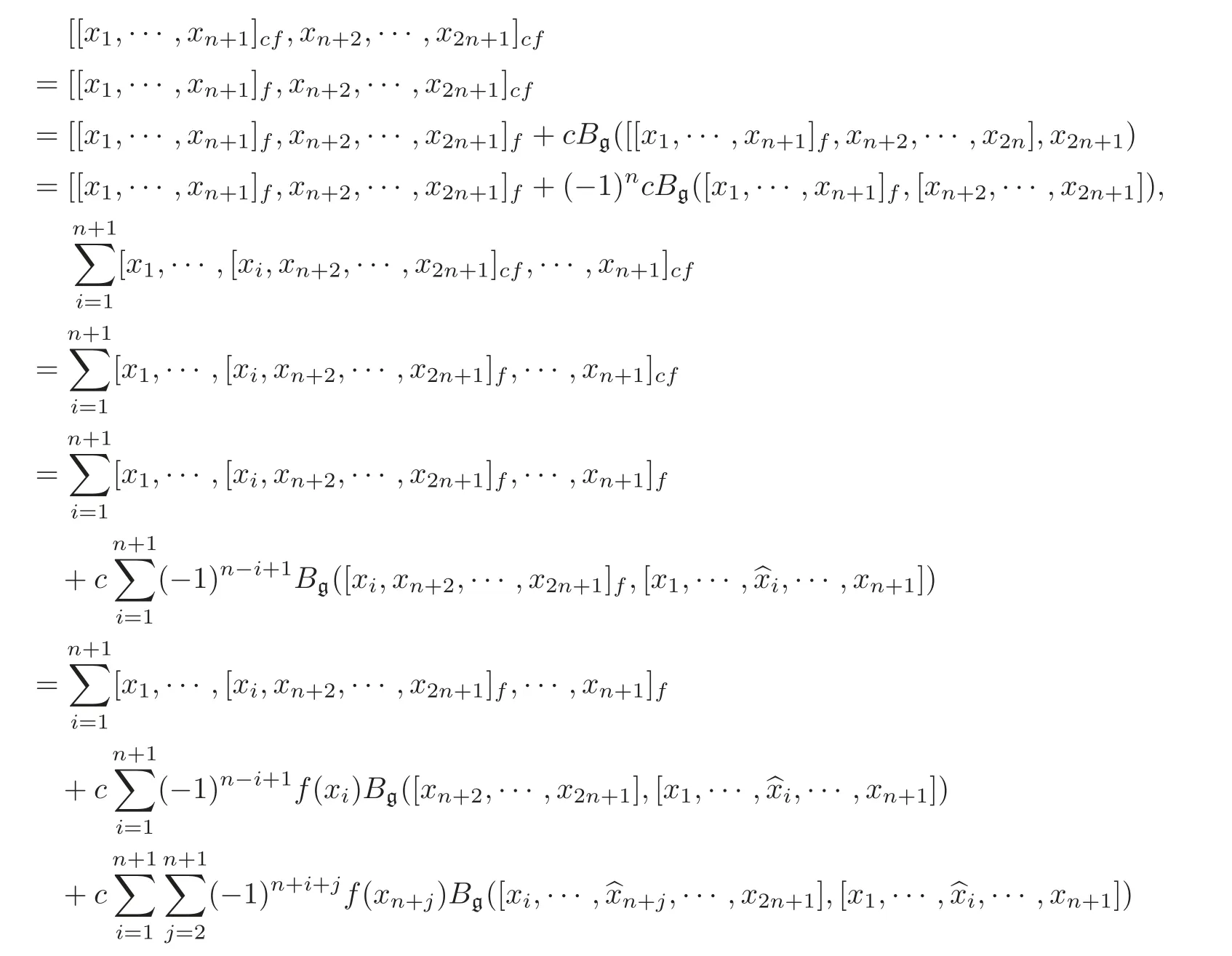
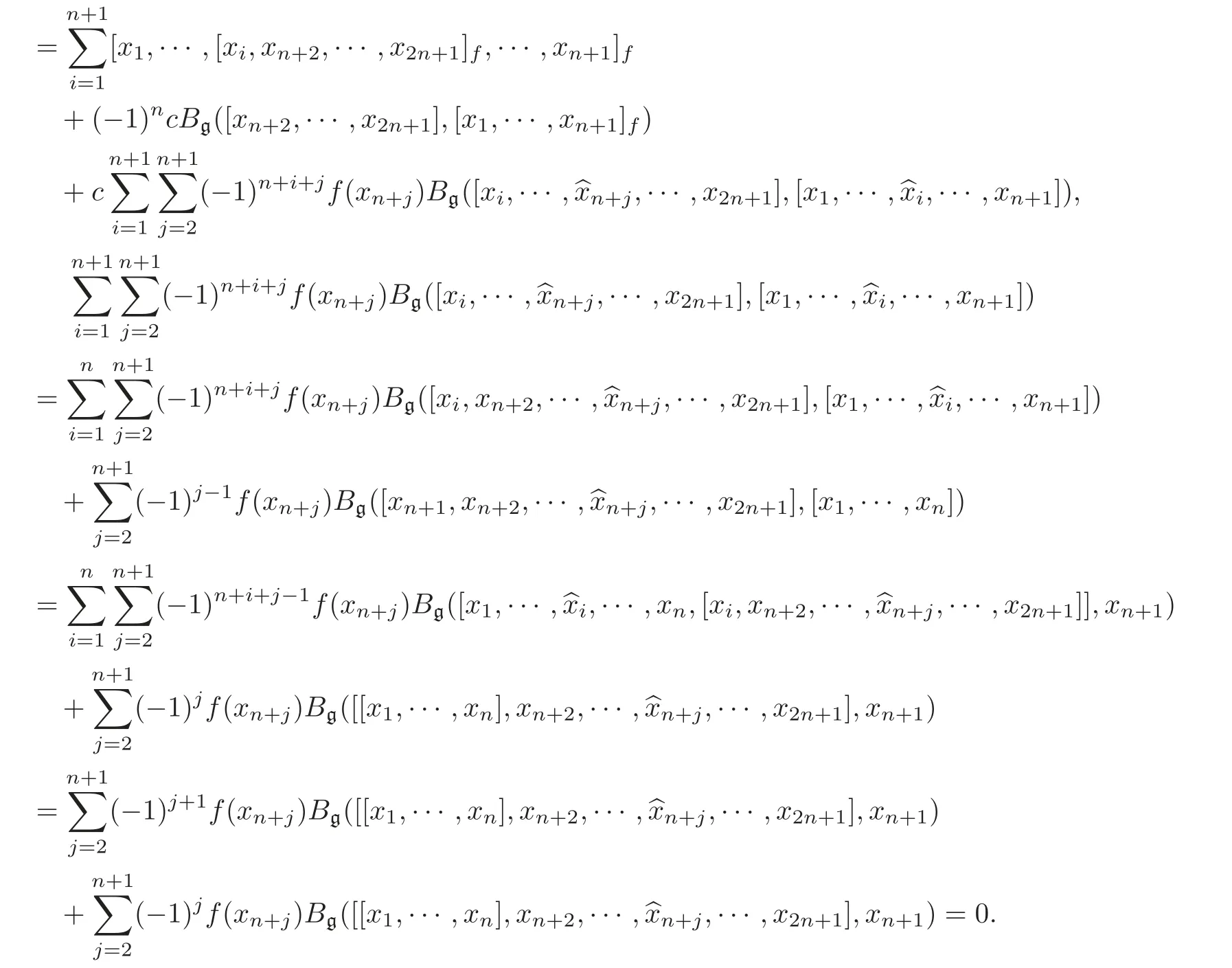
Therefore,(L,[,···,]cf)is an(n+1)-Lie algebra.

If the center Z(g)is non-isotropic,by[21,Lemma 2.3],Z(g)/⊆ Z(g)⊥=g1.There is a non-zero vector v1∈Z(g)−g1such that g=Fv1⊕g1,where g1is an ideal of g and g1⊆g1,and[v1,g1,···,g1]=0.Then,Bg|g1× g1is non-degenerate and Bg(v1,g1)=0.We can choose vectors v2,···,vm∈ g1such that{v1,···,vm}is a basis of g,and choose f ∈ g∗satisfying

Then{v1,···,vm,c}is a basis of L.Define the symmetric bilinear form B:L ⊗L → F by

where B is non-degenerate,and by Equations(3.2)–(3.3),for 1 ≤ i1,···,in+2≤ m,

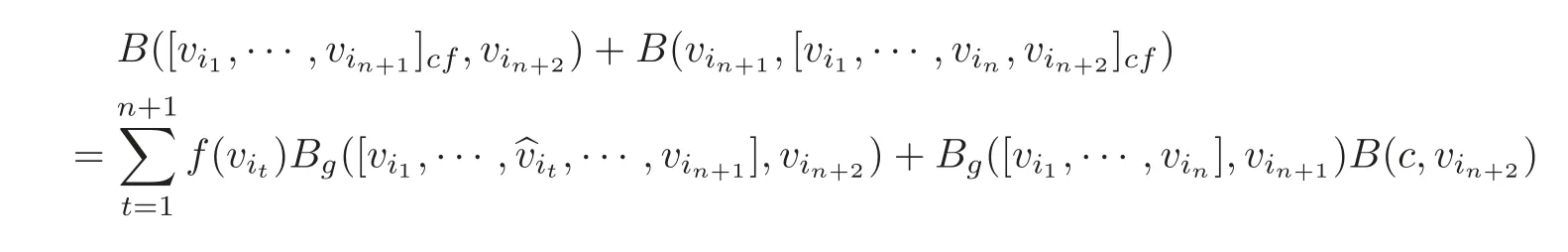
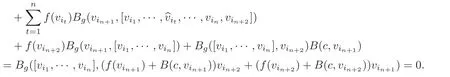
Note also that for λ∈F,

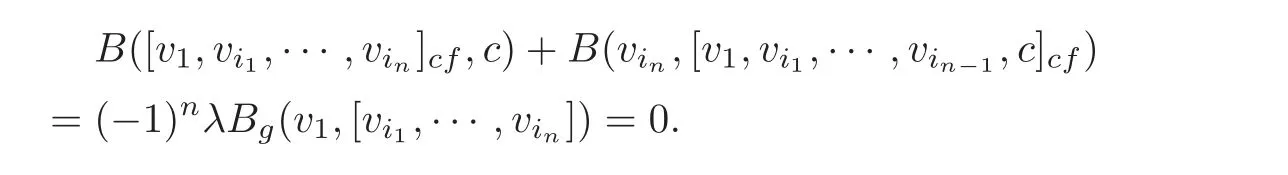
Therefore,B is a metric on the(n+1)-Lie algebra(L,[,···,]cf)and satisfies B(v,w)=Bg(v,w)for all v,w∈g.

Let A,C be n-Lie algebras.An n-Lie algebra B is called a central extension of A by C,if the sequence of n-Lie algebras

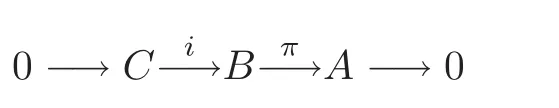
is exact and C is in the center of B.From Theorem 3.2 and Lemma 2.2,the(n+1)-Lie algebra(L,[,···,]cf)is the one-dimensional central extension of the(n+1)-Lie algebra(g,[,···,]f)by the one-dimensional abelian(n+1)-Lie algebra Fc.

Remark 3.1 Let(g,[,···,],Bg)be a metric n-Lie algebra.If the center Z(g)is isotropic,then the(n+1)-Lie algebra(L,[,···,]f)in Theorem 3.2 may not be a metric(n+1)-Lie algebra.

Example 3.1 Let(g,[,],Bg)be a metric Lie algebra with a basis{x1,x2,x3,x4,x5},and

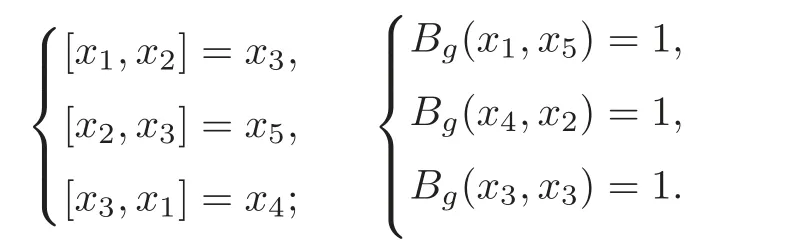
Then the center Z(g)=Fx4+Fx5is a maximal isotropic ideal.For f∈V∗with f(x1)=1 and f(xi)=0,2≤i≤5,by Theorem 3.2,we obtain a six-dimensional 3-Lie algebra(L,[,,]cf),with the multiplication[x1,x2,x3]cf=x5+c.By a direct computation,(L,[,,]cf,B)is a metric 3-Lie algebra,and Z(L)=Fx4+Fx5+Fc=Z(g)+Fc is coisotropic.

Example 3.2 Let(g,[,,],Bg)be a metric 3-Lie algebra with a basis{x1,x2,x3,x4,x5},and

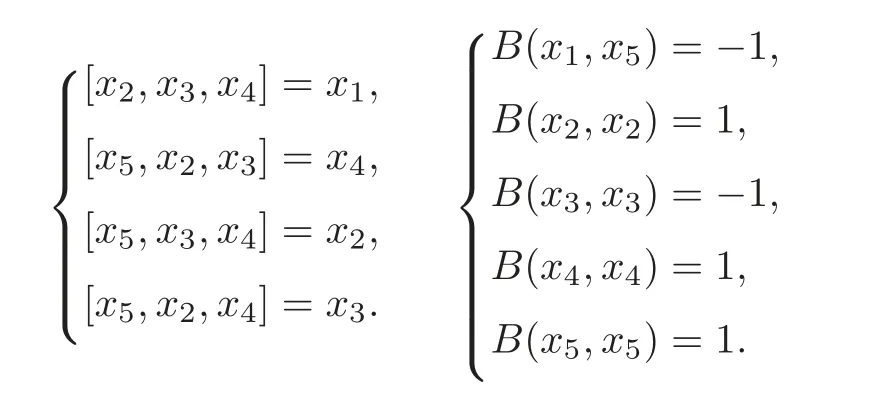
Then Z(g)=Fx1is isotropic.For f ∈ g∗,f(x5)=1 and f(xi)=0,1≤ i≤ 4,by Theorem 3.2,we obtain a six-dimensional 4-Lie algebra(L,[,,]cf)with the multiplication[x5,x2,x3,x4]cf=x1−c.By a direct computation,there does not exist a metric on(L,[,,]cf).

4 Two-Dimensional Extension of Metric n-Lie Algebras

In this section we discuss the two-dimensional extensions of metric n-Lie algebras.

Lemma 4.1(see[27])Let(g,[,···,],Bg)be an m-dimensional metric n-Lie algebra with a basis{x1,···,xm}and let x0,x−1be not contained in g.Then the vector space g0=g⊕Fx0⊕Fx−1is an(n+1)-Lie algebra under the following multiplication[,···,]0,for all natural numbers k,1≤k≤n+1,

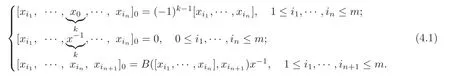
Lemma 4.2 Let(g,[,···,],Bg)be an m-dimensional metric n-Lie algebra.Then for all x1,···,xn+1,y1,···,yn−1∈ g,we have

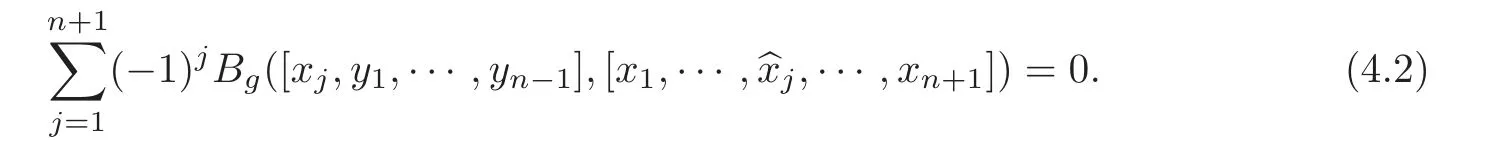
Proof By Equations(2.1)–(2.2),for all x1,···,xn+1,y1,···,yn−1∈ g,

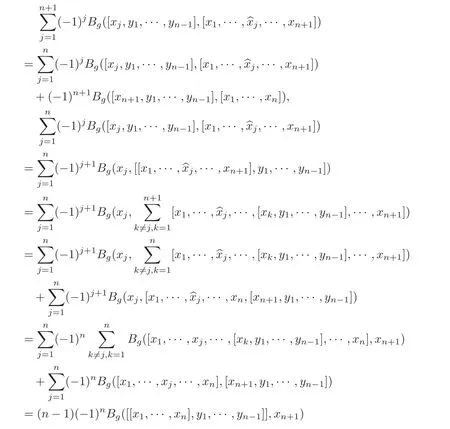
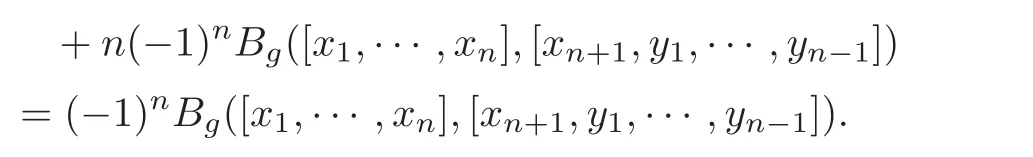
The result follows.

Theorem 4.1 Let(g,[,···,],Bg)be an m-dimensional metric n-Lie algebra with a basis{x1,···,xm}.Let 0f ∈ g∗and f(g1)=0.Suppose x0,x−1/∈ g.Then the vector space g0=g⊕Fx0⊕Fx−1is an(m+2)-dimensional(n+1)-Lie algebra in the following multiplication,for all x1,···,xn+1∈ g,1≤ k≤ n+1,

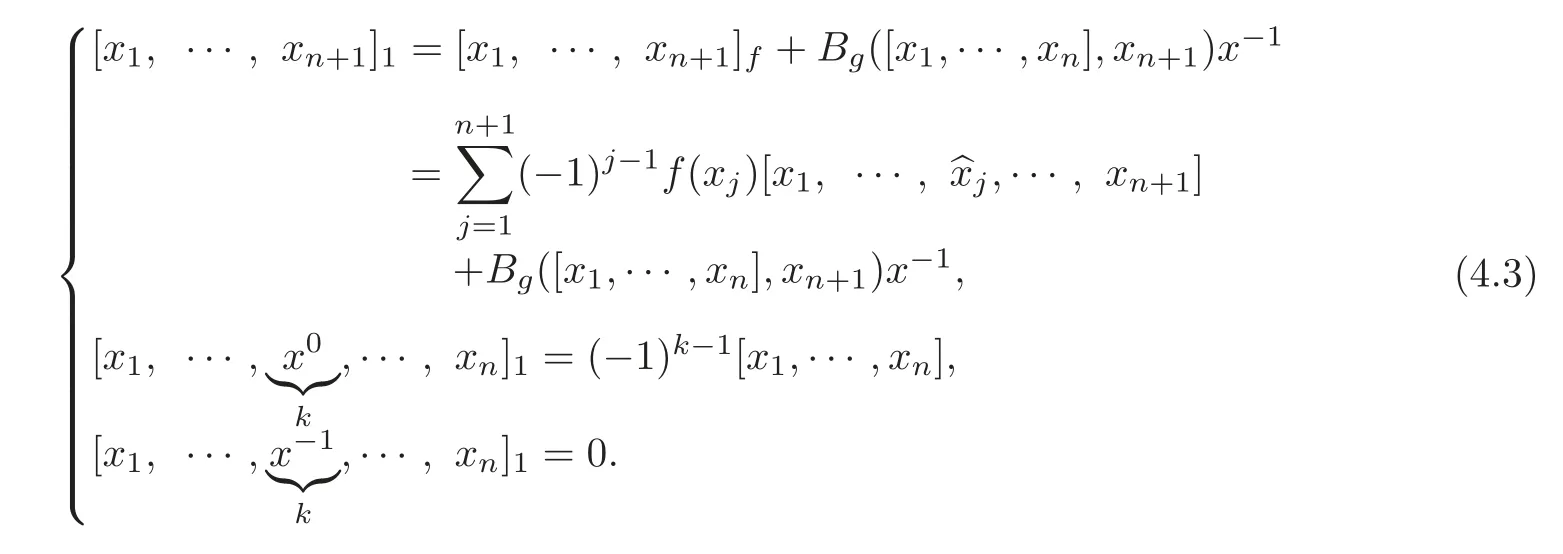
Moreover,if the center Z(g)is non-isotropic,then there is a metric B on the(n+1)-Lie algebra(g0,[,···,]1)such that B(v,w)=Bg(v,w)for all v,w ∈ g.

Proof For all x1,···,xn+1∈ g,by Equations(3.1)and(4.3),we have

[x1,···,xn+1]1=[x1,···,xn+1]x−1f,where[x1,···,xn+1]x−1fis defined as in Equation(3.1).

Then for all y1,···,yn∈ g,

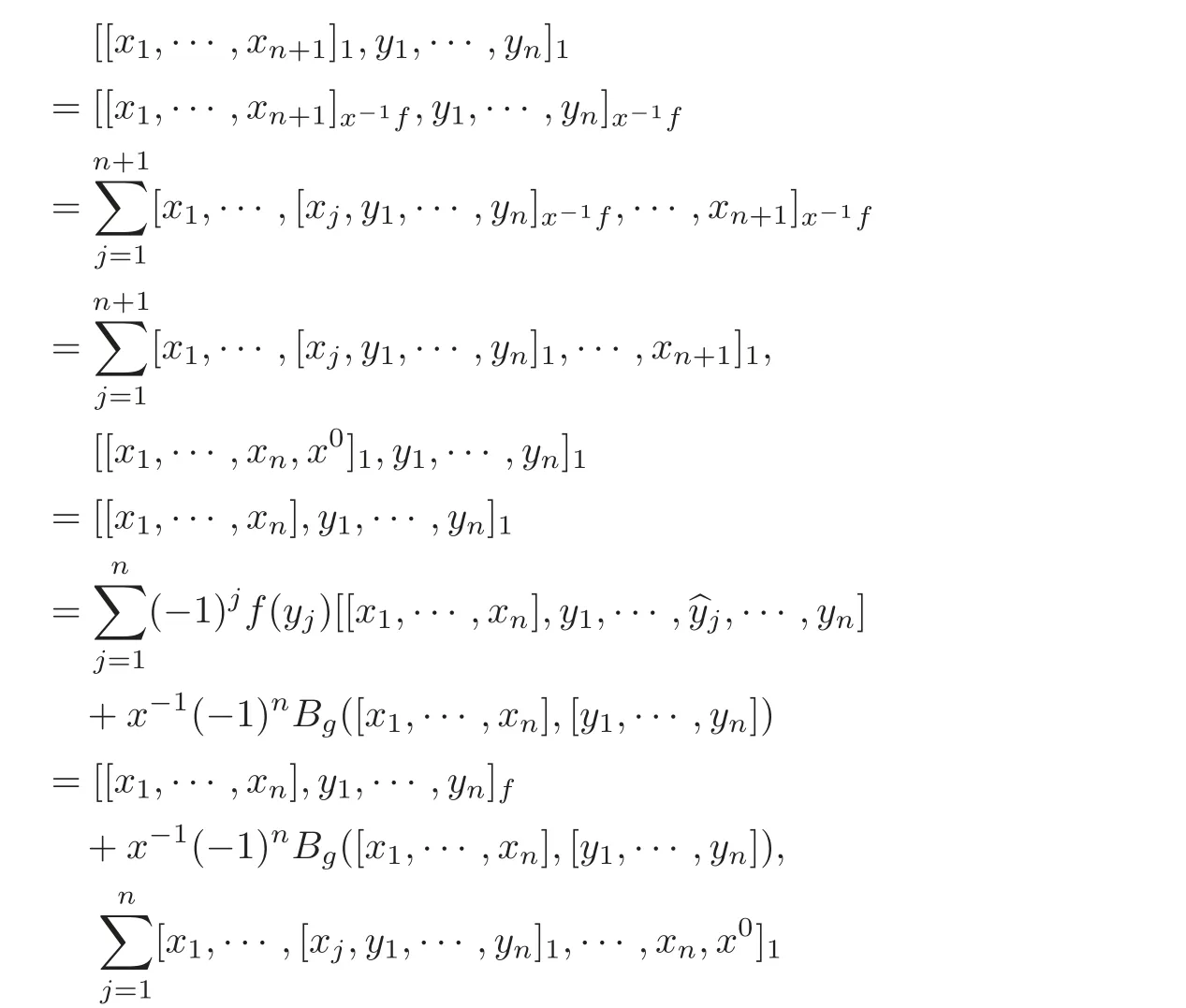
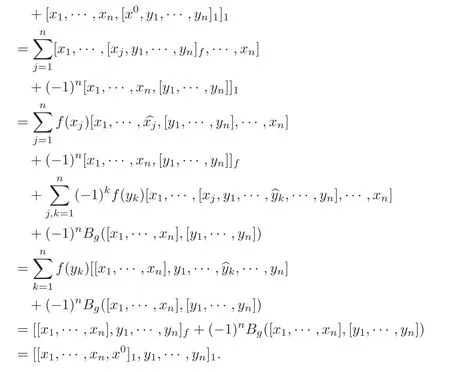
By Lemma 4.2,

Thanks to Equation(4.3),

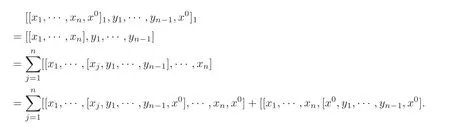
Therefore,(g0=g ⊕ Fx0⊕ Fx−1,[,···,]1)is an(n+1)-Lie algebra in the multiplication defined by Equation(4.3).

If the center Z(g)of the metric n-Lie algebra(g,[,···,],Bg)is non-isotropic,we denote g1=g⊕Fx−1.Then by Equations(4.3)and(3.1),(g1,[,···,]1)is a subalgebra of the(n+1)-Lie algebra(g0,[,···,]1).Define a linear isomorphism

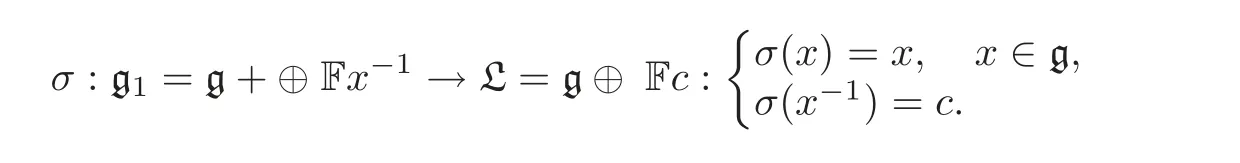
By Equations(3.1)and(4.3), σ is an algebraic isomorphism from(g1,[,···,]1)to(L,[,···,]cf).By Theorem 3.2 and Equation(3.3),there is a metric B1:g1× g1→ F such that B1|g×g=Bg.Now define B:g0×g0→F,for all x1,x2∈g,

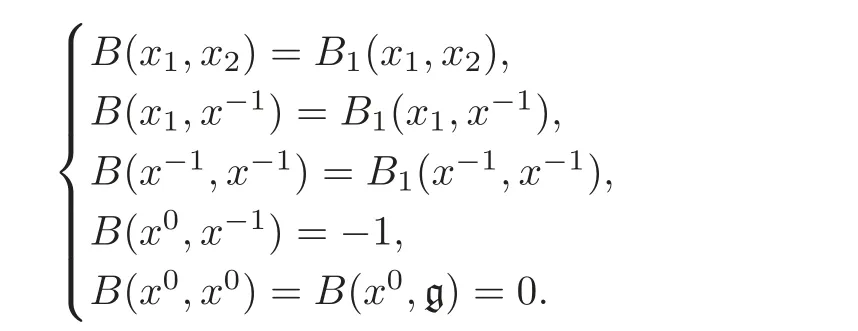
Then B is non-degenerate on g0.According to Equations(4.3)–(4.4)and a direct computation,we get that for all x1,···,xn+2∈ g,

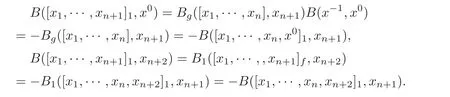
Therefore,(g,[,···,]1,B)is a metric(n+1)-Lie algebra and satisfies B|g⊗g=Bg.

Remark 4.1 Let(g,[,···,],Bg)be a metric n-Lie algebra.If the center Z(g)is isotropic,then the(n+1)-Lie algebra in Theorem 4.3 may not be a metric(n+1)-Lie algebra.The counterexample can be seen in Section 5.

Let(g,[,],Bg)be the five-dimensional metric Lie algebra in Example 3.1,and f ∈ g∗,f(x1)=1 and f(xi)=0 for 2≤i≤5.Then the center Z(g)=Fx4+Fx5is a maximal isotropic ideal.Suppose that x0,x−1are not contained in g,and g0=g⊕ Fx0⊕ Fx−1.By

Theorem 4.3,(g0,[,···,]1)is an(n+1)-Lie algebra with the multiplication

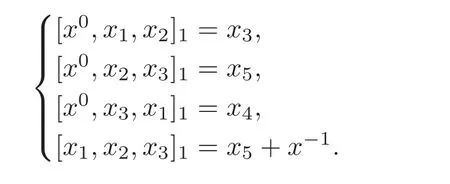
Define B:g0⊗g0→F,

By the direct computation,(g0,[,,]1,B)is a metric 3-Lie algebra,and Z(g0)=Fx4+Fx5+Fx−1=Z(g)+Fx−1is isotropic.

5 The Extensions of(n+2)-Dimensional Metric n-Lie Algebras

In this section,we give applications of Section 3 and Section 4.We provide the extensions of all(n+2)-dimensional metric n-Lie algebras.

By the paper[21]and Theorem 3.2 in[29],if(g,[,···,],Bg)is an(n+2)-dimensional metric n-Lie algebra,then(g,[,···,],Bg)is isomorphic to one and only one of the following:

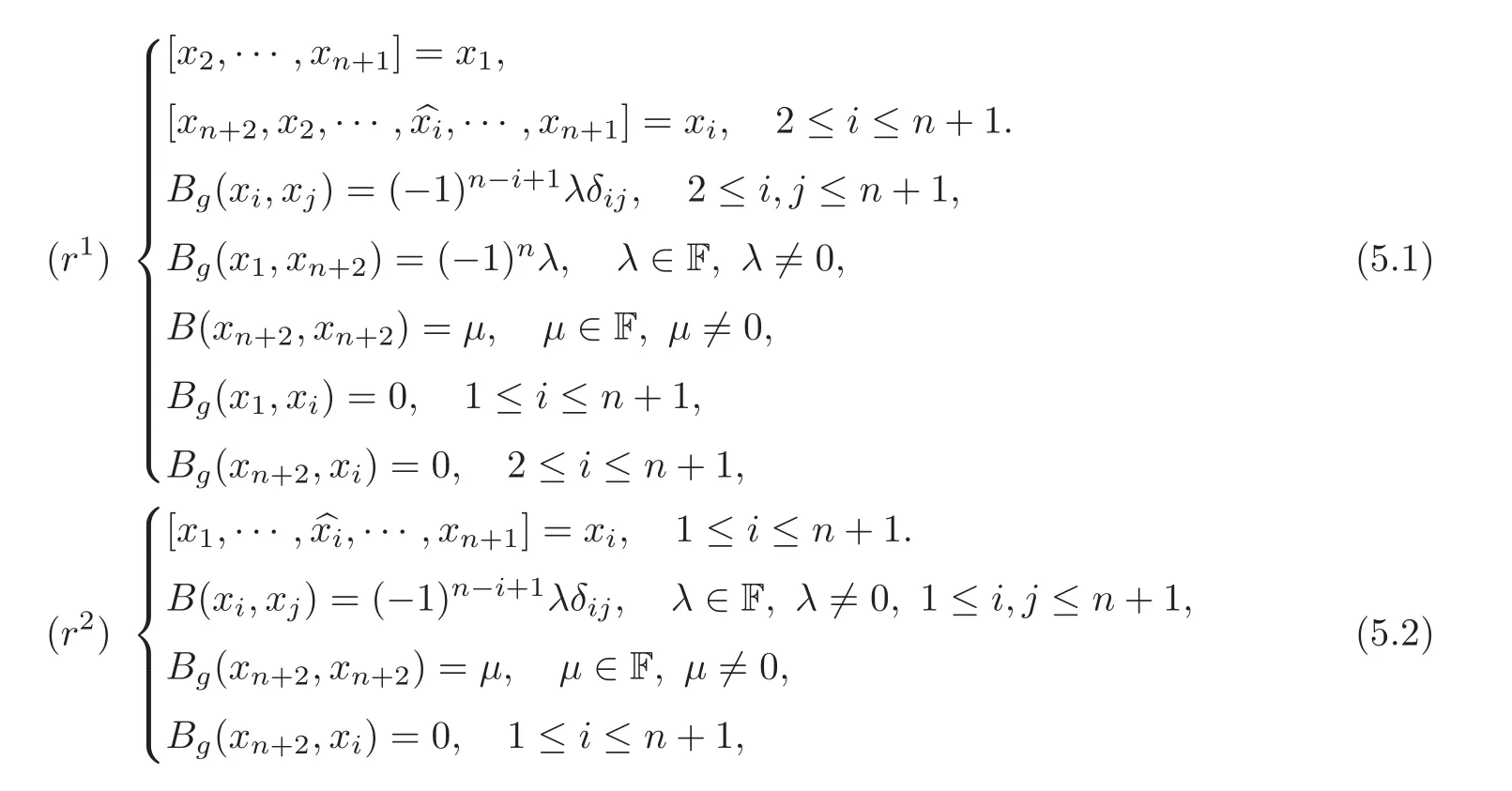
where{x1,···,xn+1,xn+2}is a basis of g and

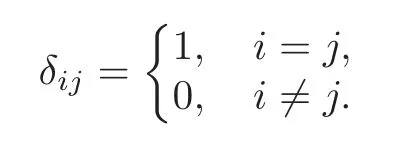
Now we discuss the extensions of the cases(r1)and(r2),respectively.

(a)Let(g,[,···,],Bg)be isomorphic to the case(r1).Then by Equation(5.1),Z(g)=Fx1is isotropic.

(ia)Let c not be contained in g.Set

and

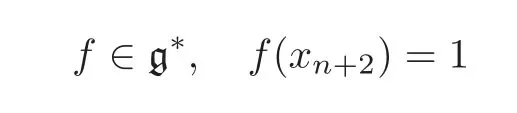
and

Then by Theorem 3.2 and Equations(3.1)and(5.1),we obtain an(n+3)-dimensional(n+1)-Lie algebra(L,[,···,]cf)with the multiplication

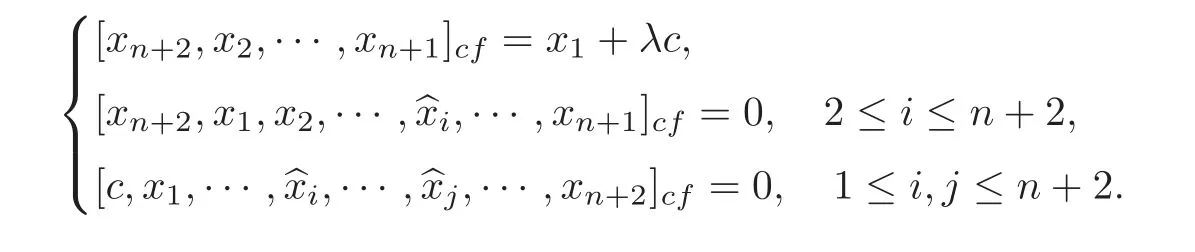
The center Z(L)=Fx1⊕Fc.

If a symmetric bilinear form B:L×L→F satisfies Equation(2.2),then by a direct computation we get B(x1+λc,L)=0,that is,B is degenerate.Therefore,there does not exist a metric on(L,[,···,]cf).

(iia)Let x0,x−1be not contained in g.Set

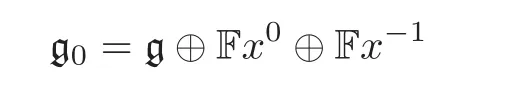
and

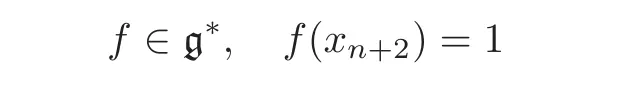
and

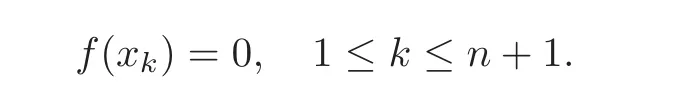
Then by Theorem 4.3 and Equations(4.3)and(5.1),the multiplication of the(n+4)-dimensional(n+1)-Lie algebra(g0,[,···,]1)is as follows:

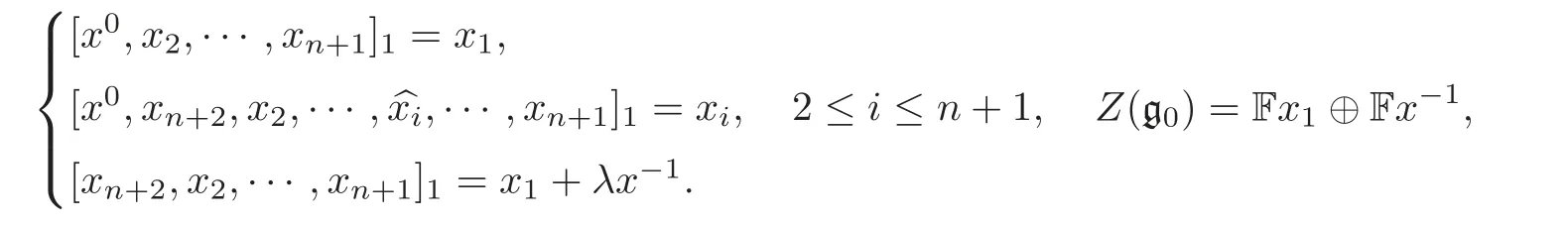
For every symmetric bilinear form B:g0⊗g0→ F satisfying B|g⊗g=Bgand Equation(2.2),we have B(x1,g0)=0,that is,B is degenerate.Therefore,there does not exist a metric on the(n+1)-Lie algebra(g0,[,···,]1).

(b)Let(g,[,···,],Bg)be isomorphic to the case(r2).Then by Equation(5.2),Z(g)=Fxn+2is non-isotropic.

(ib)Let c not be contained in g.Set

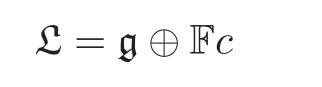
and

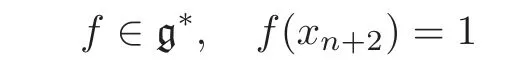
and

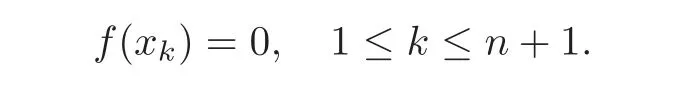
Then by Theorem 3.2 and Equations(3.1)and(5.2),the multiplication and the metric of the(n+3)-dimensional metric(n+1)-Lie algebra(L,[,···,]cf,B)are as follows:

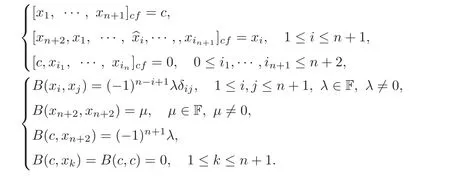
The center Z(L)=Fc is isotropic.

(iib)Let x0,x−1not be contained in g.Set

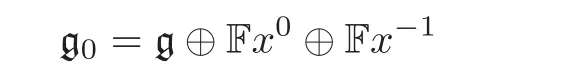
and

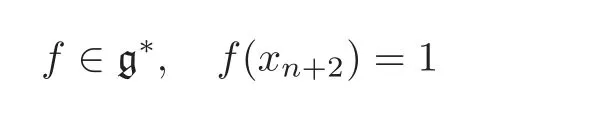
and

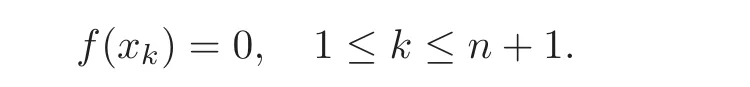
Then by Theorem 4.3 and Equations(4.3)–(4.4)and(5.2),the multiplication and the metric of(g0,[,···,]1,B)are as follows:

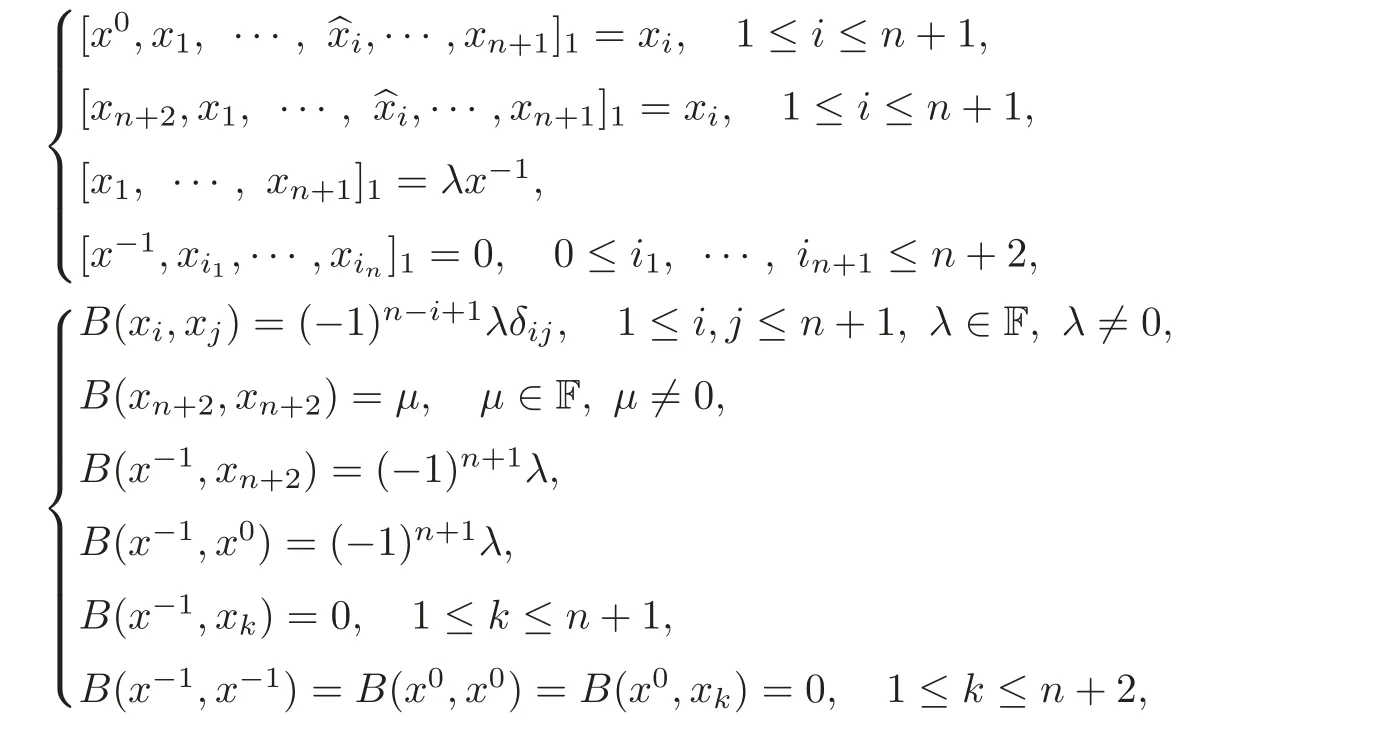
and Z(g0)=Fx−1+F(xn+2−x0)is non-isotropic.

[1]Filippov,V.T.,n−Lie algebras,Sib.Mat.Zh.,26,1985,126–140.

[2]Nambu,Y.,Generalized Hamiltonian dynamics,Phys.Rev.D,7,1973,2405–2412.

[3]Takhtajan,L.,On foundation of the generalized Nambu mechanics,Comm.Math.Phys.,160,1994,295–315.

[4]Bagger,J.and Lambert,N.,Gauge symmetry and supersymmetry of multiple M2-branes,Phys.Rev.D,77,2008,065008.

[5]Ho,P.,Hou,R.and Matsuo,Y.,Lie 3-algebra and multiple M2-branes,arXiv:0804.2110.

[6]Ho,P.,Chebotar,M.and Ke,W.,On skew-symmetric maps on Lie algebras,Proc.Royal Soc.Edinburgh A,113,2003,1273–1281.

[7]Gustavsson,A.,Algebraic structures on parallel M2-branes,arXiv:0709.1260.

[8]Papadopoulos,G.,M2-branes,3-Lie algebras and Plucker relations,arXiv:0804.2662.

[9]Hoppe,J.,On M-algebras,the quantisation of Nambu-mechanics,and volume preserving diffeomorphisms,Helv.Phys.Acta,70,1997,302–317,arXiv:hep-th/9602020v1.

[10]Ling,W.,On the structure of n-Lie algebras,University-GHS-Siegen,1993.

[11]Kasymov,S.,On a theory of n-Lie algebras,Algebra i Logika,26,1987,277–297.

[12]de Azcrraga,J.A.and Izquierdo,J.M.,n-ary algebras:A review with applications,J.Phys.A:Math.Theor.,43,2010,293001,arXiv:1005.1028[math-ph].

[13]de Azcrraga,J.A.and Izquierdo,J.M.,Cohomology of Filippov algebras and an analogue of Whitehead’s lemma,J.Phys.Conf.Ser.,175,2009,1–24.

[14]Williams,M.P.,Nilpotent N-Lie algebras,North Carolina State University,2004.

[15]Bai,R.,Shen,C.and Zhang,Y.,3-Lie algebras with an ideal N,Linear Alg.Appl.431,2009,673–700.

[16]Bai,R.,Han,W.and Bai,C.,The generating index of an n-Lie algebra,J.Phys.A:Math.Theor.,44,2011,185201,14.

[17]Dzhumadildaev,A.S.,Identities and derivations for Jacobian algebras,arXiv:0202040v1[math.RA].

[18]Medeiros,P.,Figueroa-O’Farrill,J.,Mndez-Escobar,E.and Ritter,P.,Metric 3-Lie algebras for unitary Bagger-Lambert theories,J.High Energy Phys.,0904:037,2009,arXiv:0902.4674.

[19]Jin,Y.,Liu,W.and Zhang,Z.,Metric n-Lie algebras,Commn.Algebra,39(2),2011,572–583.

[20]Jin,Y.,Liu,W.and Zhang,Z.,Real simple n-Lie algebras admitting metric structures,J.Phys.A:Math.Theor.,42(48),2009.

[21]Bai,R.,Wu W.,Li,Z.,Some results on metric n-Lie algebras,Acta Methematics Sinica,English Series,28(6),2012,1209–1220.

[22]Pozhidaev,A.P.,Monomial n-Lie algebras,Algebra and Logic,37(5),1998,307–322.

[23]Pozhidaev,A.P.,Simple n-Lie algebras,Algebra and Logic,38(3),1999,181–192.

[24]Ho,P.,Imamura,Y.and Matsuo,Y.,M2 to D2 revisited,J.High Energy Phys.,0807:003,2008,arXiv:0805.1202.

[25]Bai,R.,Bai,C.and Wang,J.,Realizations of 3-Lie algebras,J.Math.Phys.,51,2010,063505.

[26]Bai,R.and Wu,Y.,Constructing 3-Lie algebras,arXiv:1306.1994v1[math-ph].

[27]Bai,R.,Wu,W.,Li,J.and Zhou,H.,Constructing(n+1)-Lie algebras from n-Lie algebras,J.Phys.A:Math.Theor.,45,2012,475206,10 pages.

[28]Bai,R.,Han,W.and Liu,H.,Structures of 2-step nilpotent 3-Lie algebras,Antarctica J.Math.,9(1),2012,23–40.

[29]Bai,R.,Song,G.and Zhang,Y.,On classification of n-Lie algebras,Front.Math.China,6(4),2011,581–606.