Mean Value of Kloosterman Sums over Short Intervals∗

Yaming LU

1 Introduction

It is well known that various kinds of exponential sums play an important role in number theory,and one of these is the classical Kloosterman sum defined by

where e(x)=e2πixandsatisfiesa ≡ 1(mod q).A famous estimate of this sum is

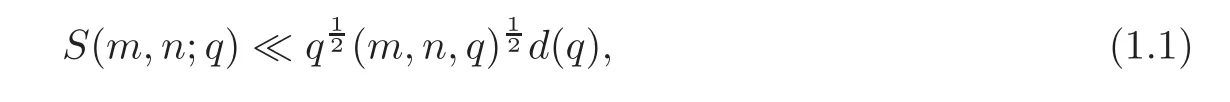
with d(q)being the divisor function,and(m,n,q)being the greatest common divisor of m,n and q.

A great deal of subjects involving this sum have been studied,and one of the interesting problems is to study the sum of Kloosterman sums.Many results have been given to date.For instance,when p is an odd prime,Kloosterman in[1]proved the identity

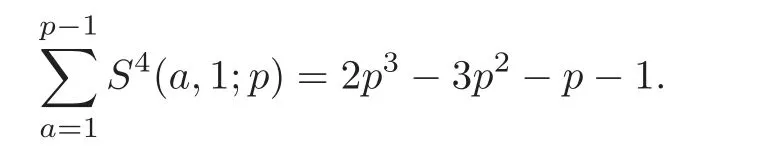
Sali´e[2]and Davenport gave

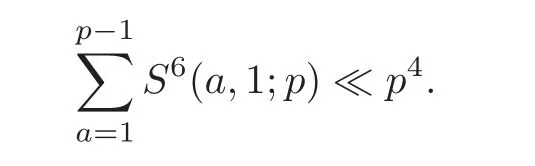
Although it seems that hardly any results have been given for the mean values over short intervals,this is indeed one of the problems that will be studied in this paper.

This work is mainly concerned with the mean value of Kloosterman sums of the following type:

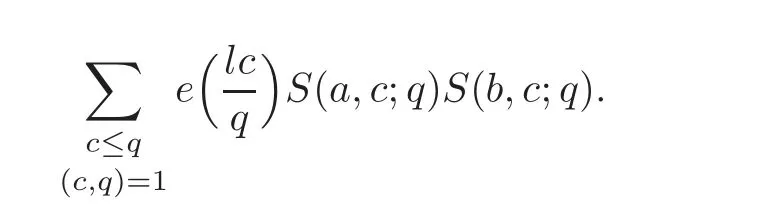
The main theorem can be described as follows.

Theorem 1.1 Let q≥3 be an arbitrary integer,and a,b,u,v be four integers satisfying u|q,v|q,(a,u)=(b,v)=1.Then we have

where ‖x‖ is the distance of x from the nearest integer,and ω(q)denotes the number of different prime divisors of q.

Based on this inequality,we will investigate the mean value properties of Kloosterman sums in short intervals,and obtain the following theorem.

Theorem 1.2 Suppose that q≥3 is an integer,and(a,q)=(b,q)=1.For N≤q,we have

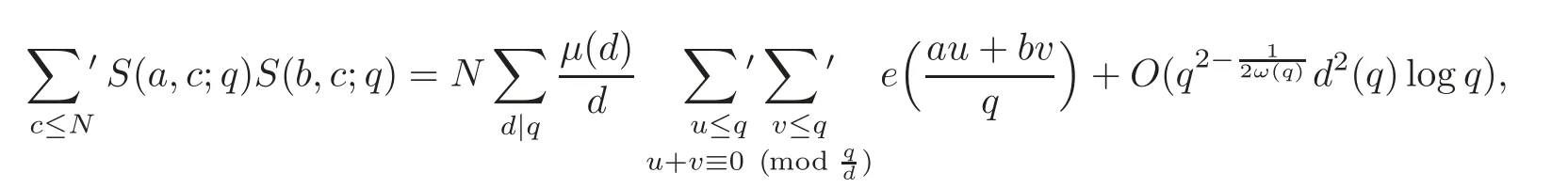
where μ(n)is a Mbius function,and

A much simpler result can be obtained while a=b.

Corollary 1.1 Suppose that q≥3 is an integer,which can be written in the form q=Q1Q2with(Q1,Q2)=1,μ(Q2)0 and Q1being a squarefull number(i.e.,p|Q1=⇒ p2|Q1).Then for(a,q)=1 and N≤q,

Especially when q is an odd prime,we have

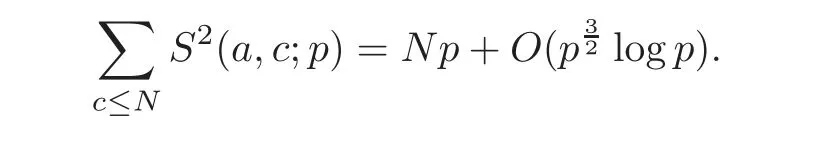
From these we may reckon that the distribution of S2(a,c;q)((a,q)=1)is quite “average”when c runs through the reduced residue class modulo q.

Remark 1.1 For a positive integer n,{a,n}stands for the multiple inverse of a modulo n,that is

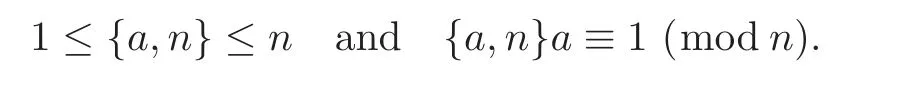
2 Auxiliary Lemmas

This section is devoted to the preparations for the proof of the theorems.

Lemma 2.1 Let p be a prime number,and α and β be two integers with α ≥ β ≥ 1.Then

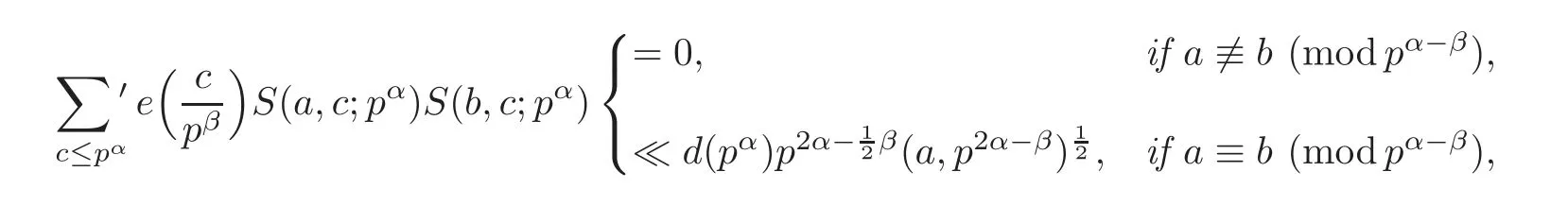
where the dash indicates that the sum runs through integers coprime with p.

Proof From the definition of Kloosterman sums,we have

where,in the last equation but one,u and v mean the multiple inverse modulo p2α−β,i.e.,u≡ v≡ 1(modp2α−β).

A special case with α = β will be discussed first.In this circumstance,

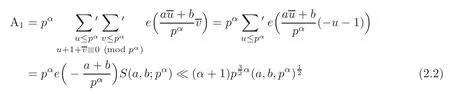
in virtue of(1.1).The calculation of A2should be split into two cases.If α＞1,then

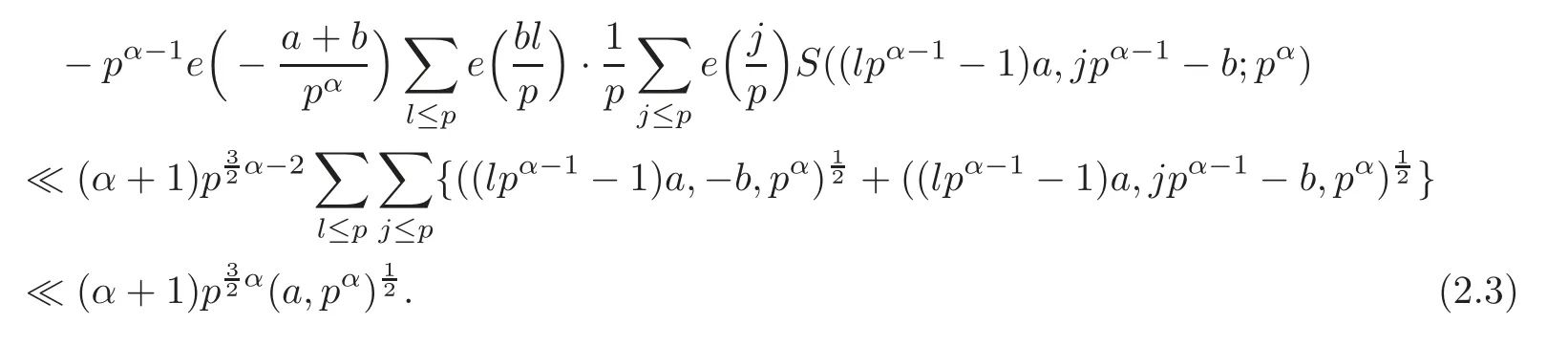
For α = β =1,we have

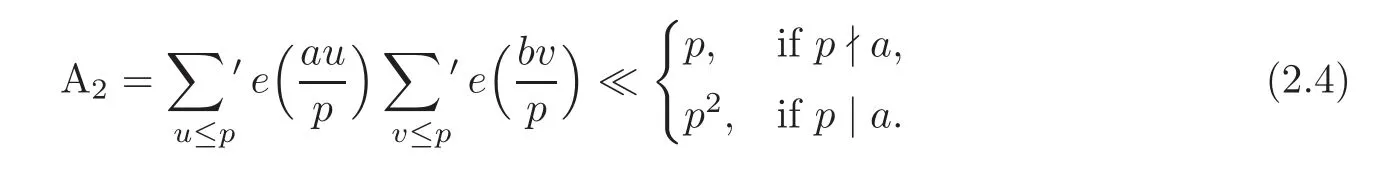
Combining(2.1)–(2.4),we complete the proof for α = β.

Now we suppose that 1≤β＜α.We still begin from the calculation of A1.

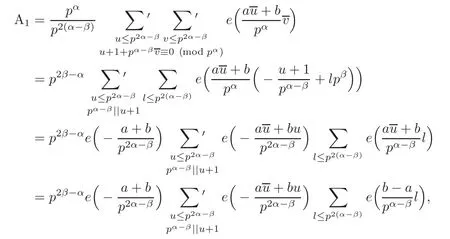
so A1=0 when a/≡ b(modpα−β).Otherwise,

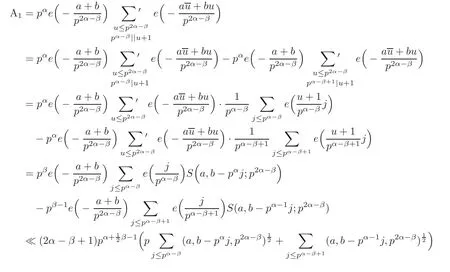
The estimation of A2is just a bit more complicated.

and we consider two different situations:

(i)β=1.Then

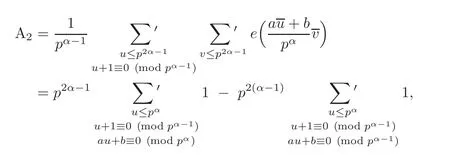
so that A2vanishes when a/≡ b(mod pα−1).Otherwise,write a=b+mpα−1and we obtain

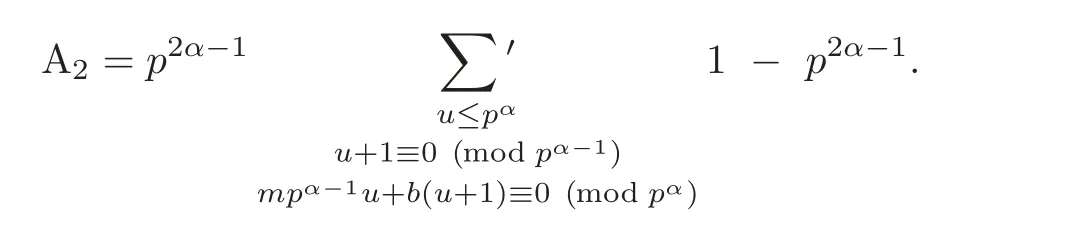
In order to make the summation on the right side of the last equation not vanishing,one of the following two conditions has to hold:

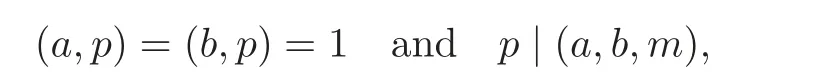
whence

(ii)β＞1.Analogous to the estimate for A1,we have

So A2=0 while a/≡ b(mod pα−β).Otherwise,we have

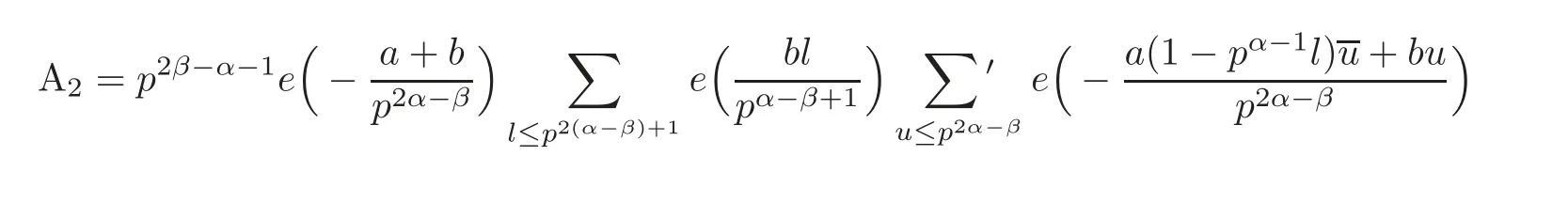
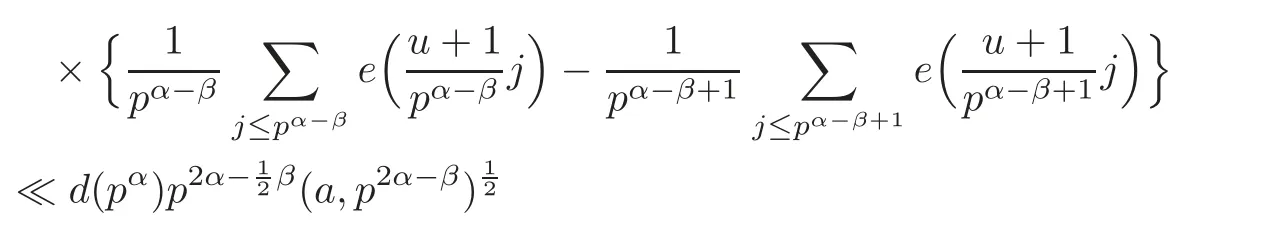
by following the similar way as in(2.5).This,with(2.5)–(2.6),gives the lemma.

Lemma 2.2 Suppose that p is a prime number,and α,β,γ,δ are four integers satisfying 1≤ β,γ,δ≤ α and δ≤ γ.Then

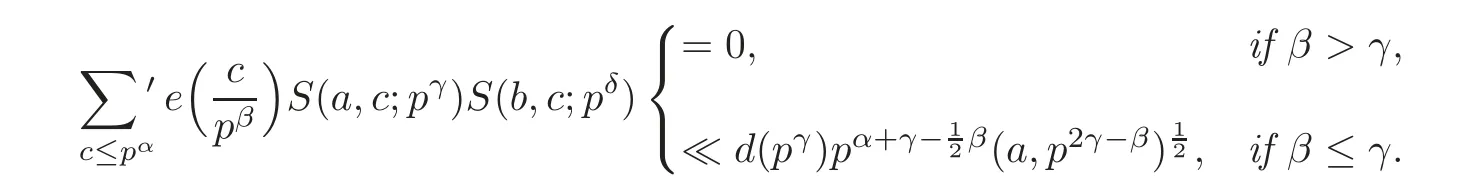
Proof We write

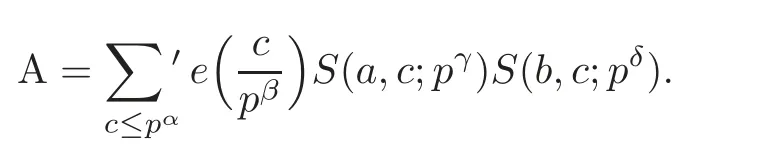
If we writeandas the integers satisfying uu ≡ 1(mod pγ)and vv ≡ 1(mod pδ)respectively,we will get

Obviously,A3=A4=0 for β ＞ γ,so we may assume β ≤ γ in the following discussion.Two cases should be considered:

(i)γ=δ.Then Lemma 2.1 implies that

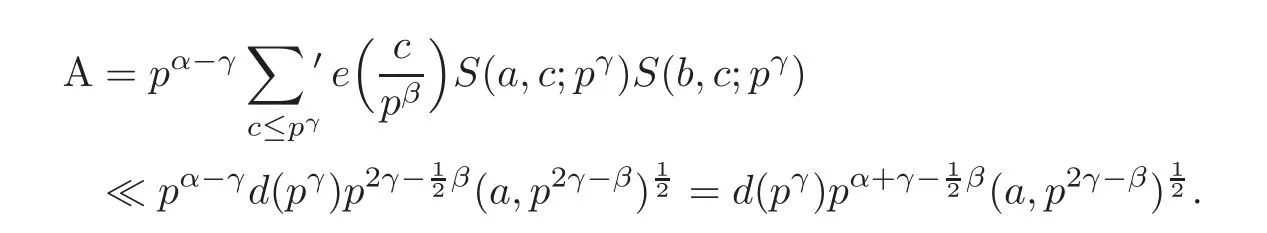
(ii) γ ＞ δ.Then we could also find that A=0 when β ＜ γ.While β = γ,we have

Besides,

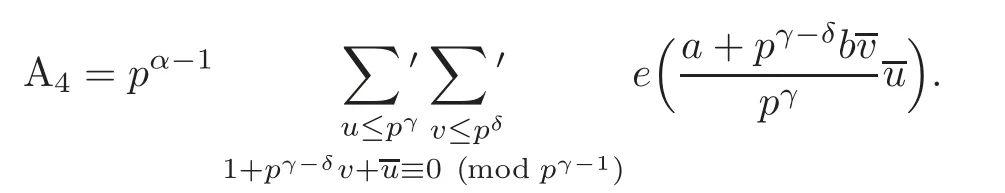
Let u= −1−pγ−δv+lpγ−1,and we have

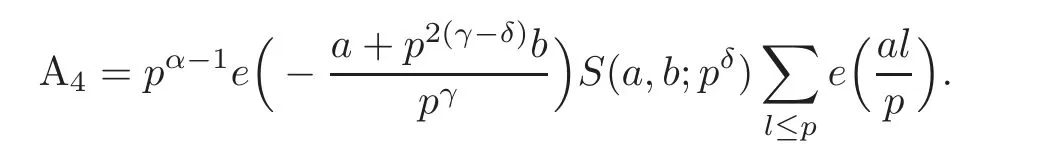
With(2.8),this gives The conclusion of the lemma holds at once.

3 Proof of the Theorems

Proof of Theorem 1.1 Suppose that the standard prime factorization of q isand put

Assume pγ||u and pδ||v,and write u=pγu′,v=pδv′.Without loss of generality,we may also assume γ ≥ δ.

Notice that S(a,c;q)is multiplicative for q,and therefore

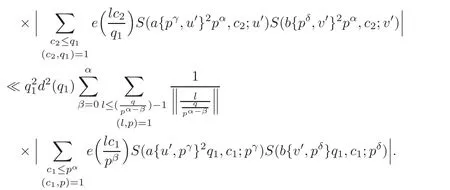
Corresponding to the case βγδ=0 and βγδ0,we use(1.1)and Lemma 2.2 respectively,so

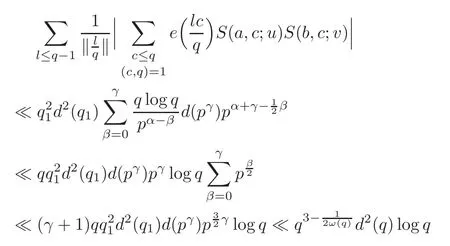
in virtue of γ ≤ α andThis completes the proof.

Proof of Theorem 1.2 Our starting point is calculating the following sum in two different ways:

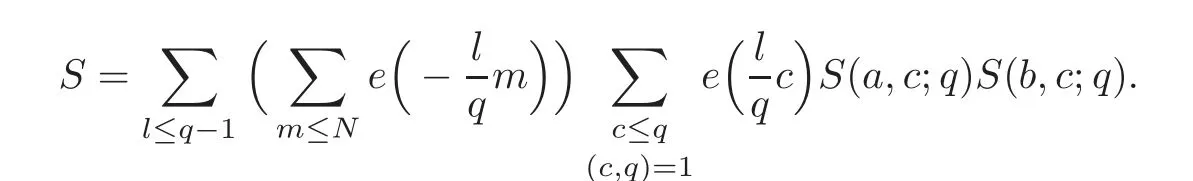
Theorem 1.1 implies that

On the other hand,changing the order of summations,we have

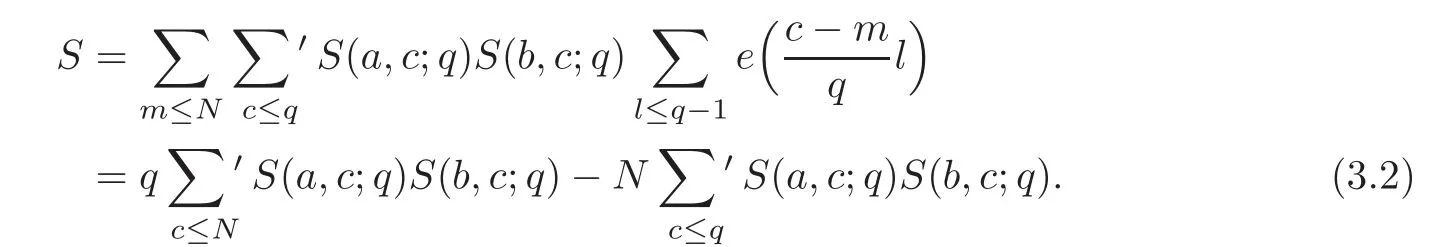
Note that

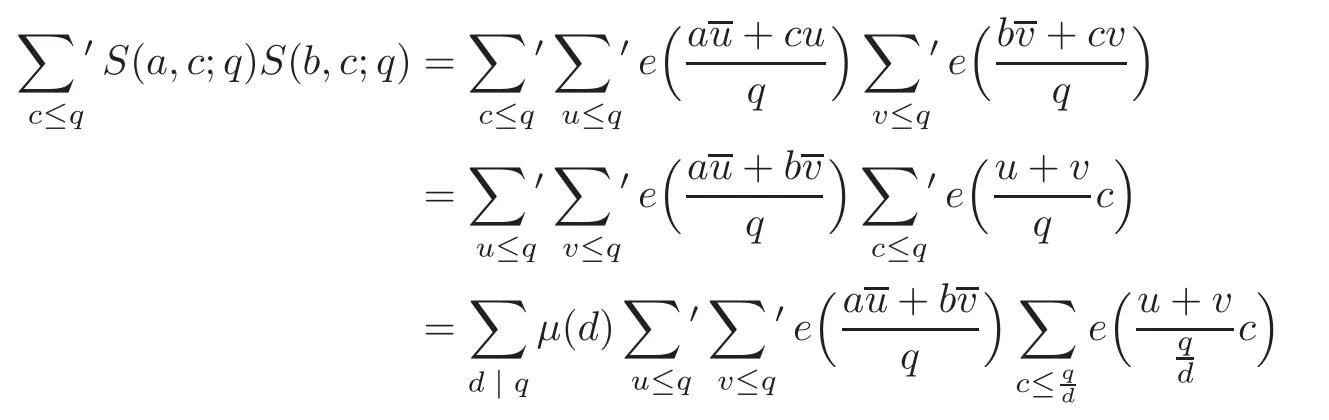
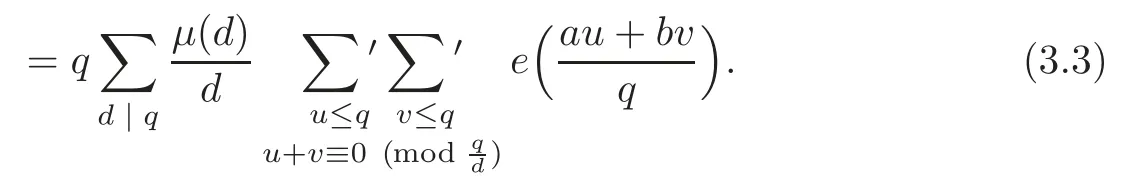
Theorem 1.2 follows immediately from(3.1)–(3.3).

Proof of Corollary 1.1 We only need to calculate

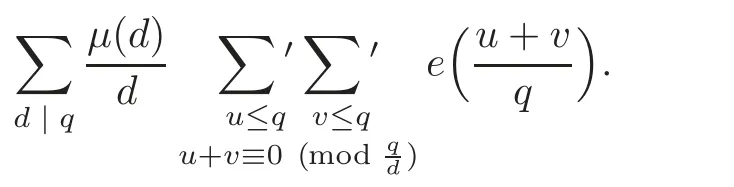
It is easy to verify that

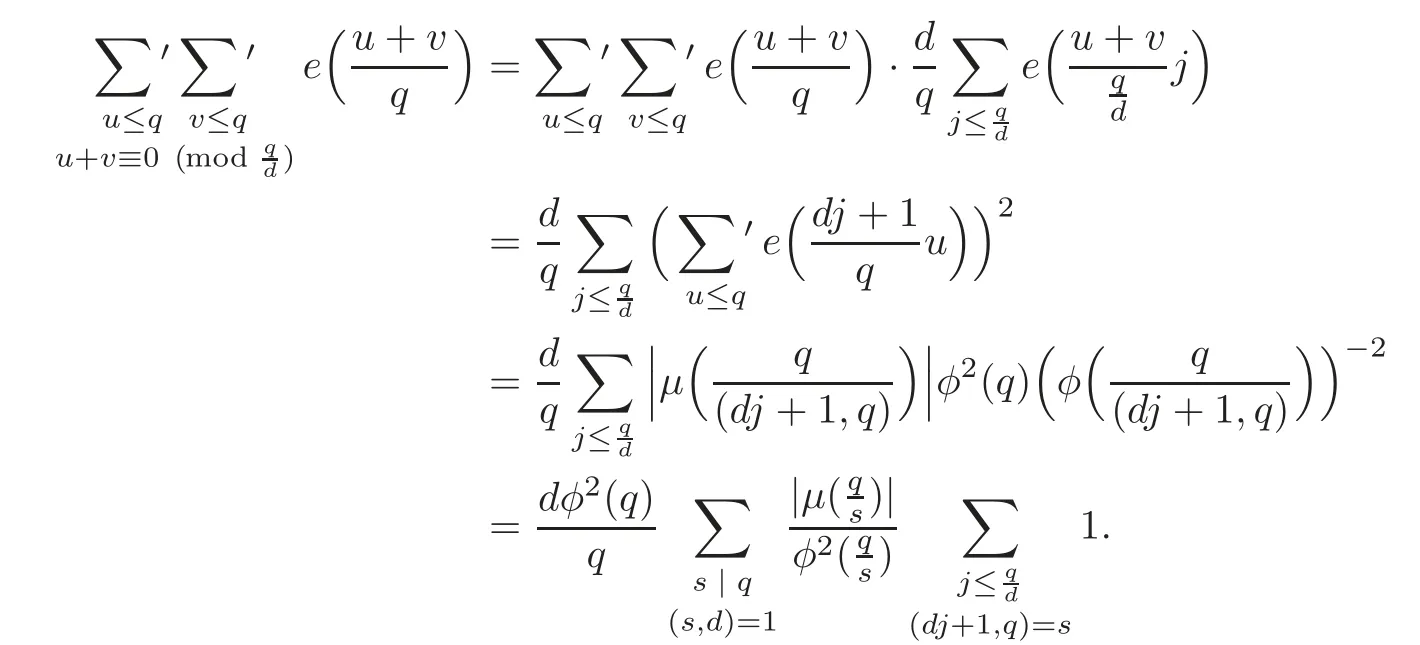
Writing dj+1=ks implies

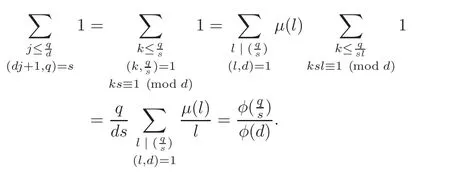
Therefore

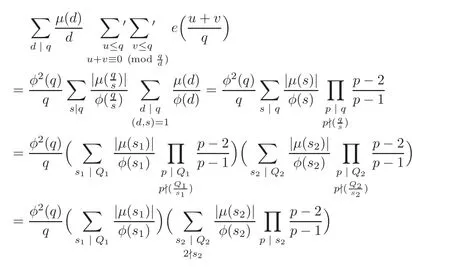
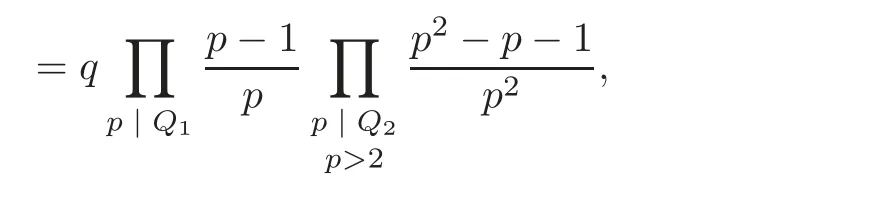
which suffices.

AcknowledgementThe author would like to thank the referee for his kindly suggestions.

[1]Kloosterman,H.D.,On the representation of numbers in the form ax2+by2+cz2+dt2,Acta.Math.,49,1926,407–464.

[2]Sali,H.,ber die Kloostermanschen summen S(u,v;q),Math.Z.,34,1931,91–109.