高压燃气管网非等温稳态模型“Newton-Rapshan”迭代法计算分析

丁国玉，李悦敏，李 进（.北京市城市规划设计研究院 北京 00045；.安徽建筑大学　合肥 060；.北京市城规技术服务中心 北京 00045）



高压燃气管网非等温稳态模型
“Newton-Rapshan”迭代法计算分析

丁国玉1，李悦敏2，李 进3
（1.北京市城市规划设计研究院 北京 100045；2.安徽建筑大学合肥 230601；3.北京市城规技术服务中心 北京 100045）

摘要：本文利用欧拉差分格式对高压燃气管网非等温稳态数学模型离散，采用Newton-Rapshan法对多点边界值条件下非等温稳态数学模型进行求解。通过与Pipeline软件计算结果对比，最大相对误差小于6%，验证了方法的可行性。

关键词：燃气管网非等温稳态模型

0　前　言

燃气管网非等温数学模型所构成的方程组为常微分方程组，确定常微分方程组的解还应给定相应的边界值条件。燃气管网非等温稳态数学模型的边界值条件主要分为单点边界值条件和多点边界值条件。当管道起点的流量、压力和温度完全明确时，求解管道其他位置的流量、压力和温度，此时为单点边界值问题。当管道起点流量、压力和温度无法全部明确时，还需在管道其他位置补充相应的已知条件，在此基础上确定管道其他位置的流量、压力和温度，此时为多点边界值问题［1］。

国内对燃气管网非等温稳态数学模型解法的研究主要集中在四阶龙格—库塔法［1-7］。四阶龙格—库塔法仅适用于单点边值问题，不适用于多点边值问题，而现实中燃气管网运行工况碰到的更多是多点边界值问题。针对上述情况，本文利用欧拉差分格式对高压燃气管网非等温稳态数学模型离散，采用Newton-Rapshan法对多点边界值条件下非等温稳态数学模型进行求解。通过与Pipeline软件计算结果分析，最大相对误差小于6%，验证了方法的可行性。

2　燃气管网非等温稳态数学模型

燃气管网主要由管道元件和压缩机、阀门、调压器等非管元件组成，因此，城市燃气管网非等温稳态数学模型由管道数学模型和非管元件数学模型组成。

2.1管道数学模型［1-2］

管道数学模型由连续性方程、动量方程和能量方程组成，如（1）-（3）式所示，描述了燃气在管道流动过程中任一管道剖分面 管道剖分面间密度ρ、压力p、温度T、焓值h和流量M等参数间的关系。

连续性方程：

动量方程：

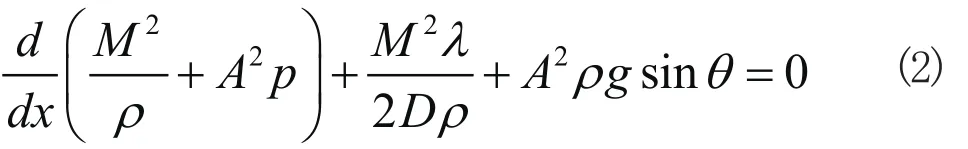
能量方程：

式中，ρ——燃气密度，kg/m³；A——管段的流通横截面积，m²；M——质量流量，kg/ s；x——管段轴向长度，m；p——气体绝对压力，Pa；2λ——摩阻系数；D——管道内径，m； g——重力加速度，m²/s；h——比焓，J/kg；K——传热系数，W/（m²·K）；T——燃气温度，K；T0——土壤温度，K。

在上式中引入真实气体状态方程p=p（ρ，T）和焓方程h=h（ρ，T），（2.1）—（2.2）式所组成的方程组未知变量为管道剖分面上的压力p、温度T和流量M。

2.2非管元件数学模型

非管元件数学模型主要为非管元件相邻剖分面间压力 、流量 和温度 的关系。常见的非管元件主要有压缩机、调压器、阀门、三通和四通等。文献［1-5］对上述非管元件的数学模型进行了详细的分析，本文不再赘述。

3　“Newton-Rapshan”法求解分析

本文求解燃气管网非等温稳态数学模型，主要通过采用差分格式将方程（1）-（3）式进行离散形成差分方程组，然后进行迭代求解。考虑到编程的难易程度及计算量，本文采用欧拉向前差分格式［8］对模型进行离散。

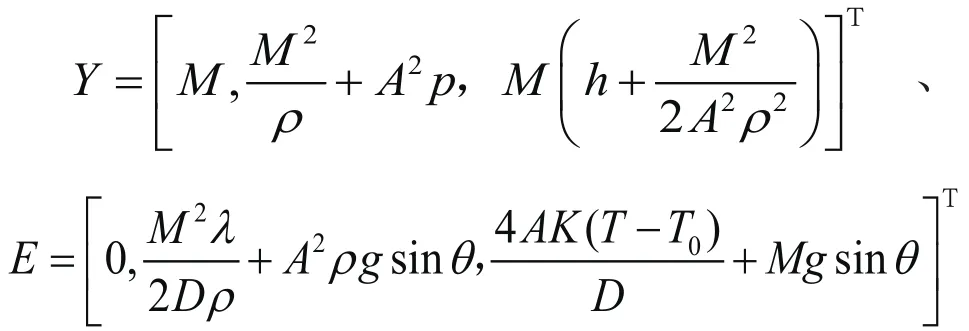
动量方程：

能量方程：

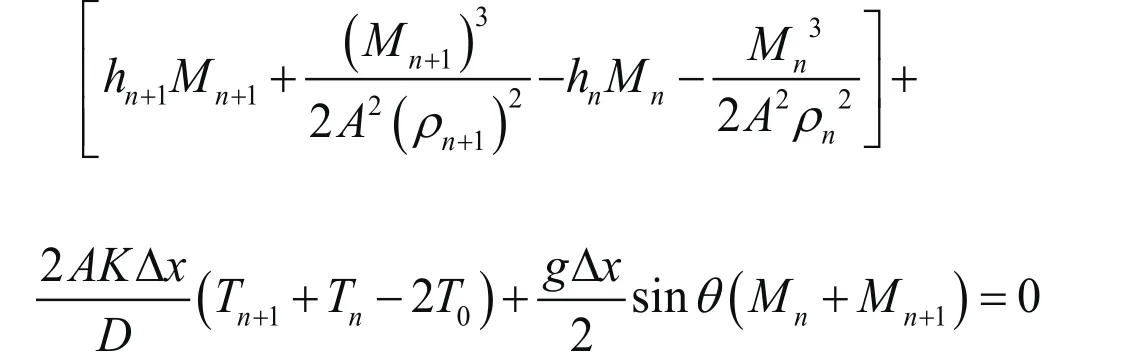
非管元件数学模型可写为：

上式中，n，n+1——管道剖分面，f——非管元件相邻管道剖分面处的压力、温度和流量方程，即f=［fp，fT，fM］T。

综上，城市燃气管网动态仿真数学模型的差分方程所形成的是一个非线性、非齐次的方程组。Newton-Rapshan迭代法的基本思想是将非线性方程组逐次线性化，从而形成的迭代算法。令X=（p0，T0，M0，…，Pn-1，Tn-1，Mn-1，）T，则差分方程组可写成Fi（x=0），i=0，1，2。设X的第K次迭代近似值为：Xk=（pk0，Tk0，Mk0，…，pkn-1，Mkn-1，）T，则迭代格式为：Xk+1=Xk-δXk，迭代增量δX=｛δp0，δT1，δM1…δpn-1，δTn-1，δMn-1｝T满足JkδXk=f（Xk）其中，J为迭代函数列f对迭代变量的Jacobi矩阵。

4　计算验证

以图1所示管网为例：由5条管道和4个节点构成。其中，节点1为气源、其余节点为分气点。管道内径D=685.5mm，管材为钢管，当量粗糙度为0.04mm，管段埋深处温度T0=278.0K，传热系数K=2。88W/m²·K；管段长度L1=L4=L5=10km，L2=L3=20km。

图1　管网示意图

假定燃气组分为甲烷，气源点压力P=4.0MPa、温度T=293.15K，调压站流量见表1。

表1　调压站流量 kg/s

计算步长取1000m；通过计算得到管段沿线压力、温度变化趋势如图2-3所示。

图2　管段沿线压力变化趋势

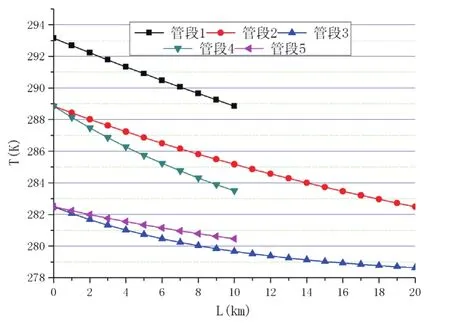
图3　管段沿线温度变化趋势

由于条件限制无法对上述模型求解结果进行实例验证，为使计算具有可比性，作者采用Pipeline软件稳态计算模块在给定气源点压力P=4.0MPa、温度T=293.15K、各分气点流量见表1、摩阻系数采用Colebrook公式的条件下对上述管网进行了计算。Pipeline软件是一套成熟的商业的软件，计算结果具有一定的参考价值。

经对比可知，本文与Pipeline软件的计算结果基本一致，详见表2。其中，压力最大相对误差为5.57%，温度最大相对误差为0.3%。造成误差的原因可能为燃气物性参数的选择及解法所造成的，但从总体上看，本文的计算方法是可以接受的，能满足一般的工程需求。

表2　计算结果对比分析

4　小结

本文利用欧拉差分格式对高压燃气管网非等温稳态数学模型离散，采用Newton-Rapshan法对多点边界值条件下非等温稳态数学模型进行求解。通过与Pipeline软件计算结果对比，最大相对误差小于6%，验证了方法的可行性。

参考文献

［1］李长俊.天然气管道输送［M］.北京：石油工业出版社，2006

［2］严明卿.燃气输配工程分析［M］. 北京：石油工业出版社出版.2007

［3］马江平.城市燃气管网动态模拟技术的研究［D］.武汉：华中科技大学，2006：36-40

［4］丁国玉.变边界条件下高压燃气管网动态仿真［D］.济南：山东建筑大学，2009：27-28

［5］沈孝风.输气干线管网瞬态模拟仿真与优化技术研究［D］.青岛：中国石油大学，2010：30-31

［6］李军.基于瞬态模拟的燃气管道泄漏检测与定位技术［D］.天津：天津城市建设学院，2013：25-27

［7］丁延鹏.天然气管输系统快瞬变流动特性研究［D］.青岛：中国石油大学（华东），2011：20-22

［8］陆金甫，关治.偏微分方程数值解法［M］.北京：清华大学出版社.1987.

Analysis on the Non-isothermal Steady Flow of High-pressure
Gas Network Based on the Method of Newton-Rapshan

DING Guoyu1，LI Yuemin2，LI Jin3
（1.Beijing Municipal Institute of City Planning &Design， Beijing ，100045；2.Anhui Jianzhu University Hefei 230601；3.Beijing Urban Planning Technical Consultancy Service Center， Beijing，100045）

Abstract：The Eulerian difference scheme is used to discrete the non-isothermal steady flow model of highpressure gas network. Based on the Newton-Rapshan method， the multi-point boundary value problem of the nonisothermal stead fow model is solved.Compared to the result got from -calculationthe Pipeline software， the error is less than 6% ， and thus the feasibility of the method has beenverifed.

Keywords：Gas network； Non-isothermal； Steady mode

作者简介：丁国玉，（1983-），男，硕士；研究方向：燃气输配及利用。

收稿日期：2015-09-21

DOI:10.11921/j.issn.2095-8382.20160218

中图分类号：TU996

文献标识码：A

文章编号：2095-8382（2016）02-092-05