浅谈初中数学发散思维能力的培养

许家苗

摘 要： 所谓发散性思维是指沿着不同的方向思考问题，寻求多样性解答的思维方式.它是一种不依常规，寻求变异，从多方面寻求答案的思维方式.这种思维方式，不受现代知识的局限，不受传统知识的束缚，与创造力有着直接的联系，是创造性思维的核心.培养发散思维能力是培养创造力的重要环节，对学生尤为重要.“激活”发散思维，促进目标教学，全面提高教学质量，因此在初中数学教学中应注重学生发散思维能力的培养.

关键词： 初中数学 发散思维 能力培养

所谓发散性思维是指沿着不同的方向思考问题，寻求多样性解答的思维方式.它是一种不依常规，寻求变异.从多方面寻求答案的思维方式.这种思维方式，不受现代知识的局限，不受传统知识的束缚，与创造力有着直接的联系，是创造性思维的核心.培养发散思维能力是培养创造力的重要环节，对学生尤为重要.“激活”发散思维，促进目标教学，全面提高教学质量，教师在教学中应大胆多向地展开想象，认真体会.

一、发散性提问

思维是从问题开始的，发散性提问可以激励学生进行积极的思维活动，这种提问追求的目标不是单一答案，而是尽可能多、尽可能新的独特想法，因而对于学生的创造性思维有更直接、更现实的意义.

如：八年级下第18、1平行四边形的判定第二节我设计了这样的提问：要判定一个四边形是平行四边形，我们已经从边和角度进行了研究，谁能说一说有哪几种方法？除了这些方法以外，还有其他方法吗？第一个问题既是对上一节教学内容的复习，又为本节课的教学做好了铺垫.第二问可让多个学生回答，同学们想出了几种不同的方法，显示出学生的思维非常活跃.

二、开放题练习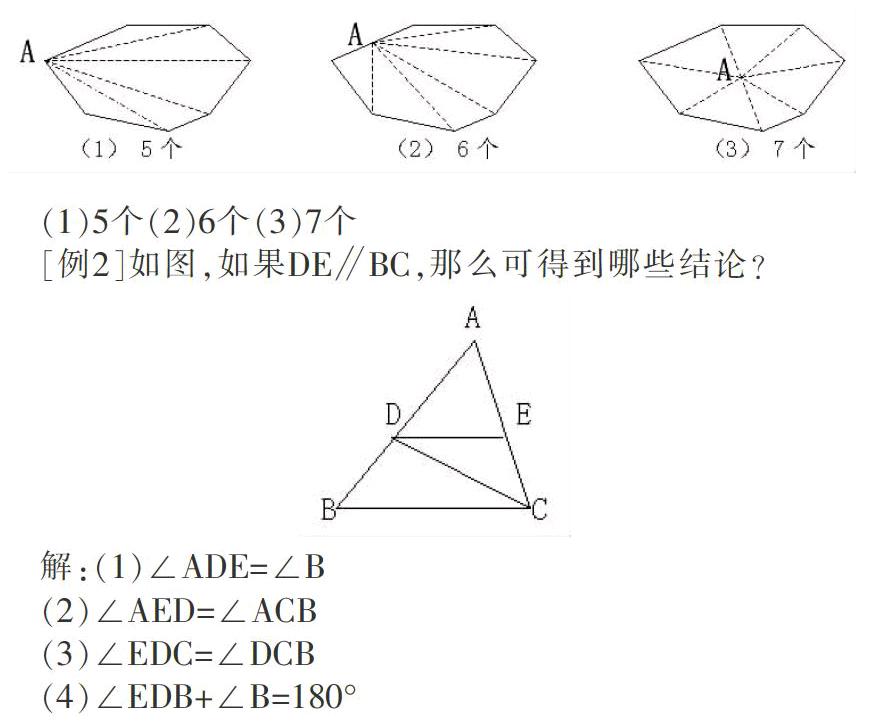

练习是数学教学的重要组成部分，恰到好处的习题，不仅能巩固知识、形成技能，而且能启发思维、培养能力.在教学过程中，我除了注意增加变式题、综合题外，还适当设计了一些开放题，培养学生思维的深刻性、灵活性和广阔性，克服呆板性.

1.运用不定型开放题，培养学生思维的深刻性.

不定型开放题，所给条件包含着答案不唯一的因素，在解题过程中，必须利用已有的知识，结合有关条件从不同角度对问题做全面分析，正确判断得出结论，从而培养学生思维的深刻性.

[例1]如图，一个七边形，请你用三种不同的方法把它分割成三角形，至少可以分割成多少个三角形.

（1）5个（2）6个（3）7个

[例2]如图，如果DE∥BC，那么可得到哪些结论？

解：（1）∠ADE=∠B

（2）∠AED=∠ACB

（3）∠EDC=∠DCB

（4）∠EDB+∠B=180°

（5）∠DEC+∠ACB=180°

2.运用多向型开放题，培养学生思维的广阔性和灵活性.

多向型开放题，对同一个问题可以有多种思考方法，使学生产生纵横联想，启发学生一题多解，一题多变，一题多思，训练学生的发散思维，培养学生思维的广阔性和灵活性

[例3]已知∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC，求：

（1）∠MON的度数.

（2）如果（1）中∠AOB=α其他条件不变，求∠MON的度数.

（3）如果（1）中∠BOC=β（β为锐角）其他条件不变，求∠MON的度数.

（4）从（1）（2）（3）的结果中能看出什么规律？

（1）解法1：∵OM平分∠AOC，ON平分∠BOC

∴∠MOC=1/2∠AOC，∠NOC=1/2∠BOC

∴∠MON=∠MOC-∠NOC

=1/2∠AOC-1/2∠BOC

=1/2（∠AOC-∠BOC）

=1/2∠AOB

∵∠AOB=90°

∴∠MON=45°

解法2：∵∠AOB=90°，∠BOC=30°

∴∠AOC=120°

∵OM平分∠AOC

∴∠AOM=1/2∠AOC=60°

∴∠BOM=90°-∠AOM=90°-60°=30°

∵ON平分∠BOC

∴∠BON=1/2∠BOC=15°

∴∠MON=∠BOM+∠BON=30°+15°=45°

（2）当∠AOB=α，∠MON=1/2∠AOB=α/2

（3）当∠BOC=β，∠MON=1/2∠AOB=45°

（4）从（1）（2）（3）的结果和（1）的解答过程得出∠MON的大小总等于∠AOB的一半而与∠BOC的大小变化无关.此题还可以由角度问题转化为线段问题.

[变题]如图已知线段AB=a延长AB至c使BC=b，点M、N分别为AC、BC的中点，求MN的长.

解：∵M是AC的中点，N是BC的中点

∴MC=1/2ACNC=1/2BC

∴MN=MC–NC=1/2AC-1/2BC

=1/2（AC–BC）=1/2AB=a/2

∴MN的长度总等于AB长度的一半，而与BC的长度变化无关

这道题（1）问中从不同的角度思考，得出不同的解法，（2）（3）体现一题多变.条件变化而结论不变，最后由求角度问题过渡到线段问题，体现一题多思.这类题可以给学生最大的思维空间，使学生从不同角度分析问题，探究数量关系，并从不同解法中找出最简捷的方法，提高学生初步的逻辑思维能力，从而培养学生思维的广阔性与灵活性.

三、集体讨论

在课堂教学中，有时也可以采取集体讨论的方法培养学生的发散思维.集体讨论可分为2人小组、4人小组或全班讨论，这样的讨论没有教师的介入，有利于学生畅所欲言，集思广益，从而引发创造性思维的产生.在集体讨论中，学生的思维处于积极状态，所以集体讨论对思维能力的培养是有益的，对学生真正理解数学知识也是有益的，从表面上看，集体讨论时似乎课堂秩序有点乱，但如果学生真正是在参与讨论，甚至大声争论，那就是学生生动、活泼、主动学习的体现.

总之，学生发散思维能力的培养，打破了封闭式传统的教学模式，教师的教学观念做到了四个转变，一是教师由课堂教学的主宰者转变为教学活动的组织者、参与者、引导者、激励者.二是课堂由优化垄断转变为全体参与，学生动了起来.三是师生关系由教与被教的关系转变为民主平等、合作的关系.四是由教师教的时间多转变为学生学的时间多，真正体现了学生为主体教师为主导的教学理念.