基于稀疏保持拉普拉斯判别分析的特征提取算法

任迎春， 王志成， 赵卫东， 彭　磊

(1. 同济大学 CAD研究中心,上海 200092；2. 嘉兴学院 数理与信息工程学院,浙江 嘉兴 314001；3. 泰山医学院 信息工程学院, 山东 泰安 271016)



基于稀疏保持拉普拉斯判别分析的特征提取算法

任迎春1,2， 王志成1， 赵卫东1， 彭磊3

(1. 同济大学 CAD研究中心,上海 200092；2. 嘉兴学院 数理与信息工程学院,浙江 嘉兴 314001；3. 泰山医学院 信息工程学院, 山东 泰安 271016)

摘要：针对稀疏保持投影算法在特征提取过程中无监督和l1范数优化计算量较大的问题，提出一种基于稀疏保持拉普拉斯判别分析的快速特征提取算法.首先通过逐类主元分析(PCA)构造级联字典,并基于该字典通过最小二乘法快速学习稀疏保持结构;其次利用学习到的稀疏表示结构正则化拉普拉斯判别项达到既考虑判别效率又保持稀疏表示结构的目的;所提算法最终转化为一个求解广义特征值问题.在公共人脸数据库(Yale，ORL和扩展Yale B)的测试结果验证了该方法的可行性和有效性.

关键词：特征提取；稀疏表示；拉普拉斯判别分析； 主元分析； 人脸识别

在诸如目标识别[1]、文本分类[2]、信息检索[3]等很多科学研究领域,数据常常以非常高维的形式出现.这些高维的数据常常难以被人理解、描述和识别.在实践中,特征提取是处理高维数据问题的有效手段[4-6],通过特征提取能够降低数据的维数,得到高维数据的有效低维表示,以便理解其内在结构及后续处理.迄今为止,人们提出了很多特征提取的方法.基于所利用的数据结构,可将这些方法分为三类:基于全局结构的方法、基于局部结构的方法和基于稀疏表示的方法.

主元分析(principal component analysis，PCA)[7]和线性判别分析(linear discriminant analysis，LDA)[8]是基于全局结构的特征提取算法,这些算法具有坚实的理论基础,易于执行和分析,应用广泛.但PCA和LDA均基于高维数据空间的嵌入子空间是线性的这一假设, 难以发现隐藏在高维数据中的局部流形特征.

为充分挖掘隐藏在高维数据中的局部流形结构,人们提出了多种基于流形学习的特征提取算法,主要包括等距映射 (isomap)[9]、拉普拉斯映射LE(Laplacian eigenmaps)[10]、局部线性嵌入 LLE(local linear embedding)[11]、局部保持投影LPP (locality preserving projection)[12]和邻域保持嵌入NPE (neighborhood preserving embedding)[13]等. 这些方法均通过构造近邻图保留样本的局部邻域结构,在一定程度上保持了原始数据的局部流形特征,但它们都是从局部的角度考虑,并未考虑原始样本空间中两个相距较远的样本在投影后的关系.

稀疏保持投影(sparsity preserving projection，SPP)[14]是最近提出的一种基于稀疏表示理论的无监督降维算法.该算法以保持数据的稀疏重构关系为目的,是一种较好的特征提取算法,但处理过程中计算每个样本的稀疏向量都需要求解一个l1范数优化问题,计算复杂度太高.另外,SPP并没有利用类标信息,而针对分类和识别问题,标签信息非常重要.

本文针对稀疏保持投影算法(SPP)在特征提取过程中无监督和l1范数优化计算量较大的问题,提出一种基于稀疏保持拉普拉斯判别分析的快速特征提取算法(sparsity preserving Laplacian discriminant analysis, SPLDA). 具体来讲,SPLDA首先通过逐类PCA构造级联字典并基于该字典通过最小二乘法快速学习稀疏保持结构,其次利用学习到的稀疏表示结构正则化拉普拉斯判别分析来达到既考虑判别效率又保持稀疏表示结构的目的,最后通过求解一个广义特征值问题来获得数据的最优嵌入函数. SPLDA具有以下几方面的优点：① SPLDA是一种新的特征提取方法,它在保持数据稀疏表示结构的同时又可以寻求最优的判别函数.② SPLDA在运行时间上远远优于SPP. SPLDA通过最小二乘法快速学习稀疏系数向量,而SPP需要求解n个l1范数的优化问题,两者相比SPLDA学习稀疏表示结构的计算成本大大降低.③ SPLDA两次利用了类标信息.首先在构造级联字典和计算稀疏系数向量时利用了标签信息,这有利于求解一个更具判别性的稀疏表示结构;其次在计算局部散度矩阵和非局部散度矩阵时也利用了类标信息,这更有利问题的分类.④ SPLDA引入了吉洪诺夫正则项[15],有效克服了局部散度矩阵的奇异性问题,因此SPLDA对小样本问题同样适用.

1稀疏保持投影

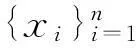
(2)其中，si是式(1)的最优解，表示每个样本xi的稀疏向量系数. 最后，通过求解如下的优化问题得到最优投影向量

(3)其中，Sβ=S+ST-STS,该优化问题最终转化为求解一个广义特征值问题.

从上述算法步骤可以看出,SPP在构造稀疏权重矩阵时需求解n个l1范数的最小化问题,这对于大规模问题由于计算代价太大而无法广泛应用;另外,SPP是一种无监督学习模式,而对于分类和识别问题,充分利用类标信息是十分重要的.

2SPLDA算法

针对SPP在构造稀疏权重矩阵时需要求解n个l1范数计算量较大的问题,本文借助逐类PCA构造级联式约简字典,并基于该字典通过最小二乘法快速学习稀疏保持结构;针对SPP在维数约简过程中的无监督问题,本文充分利用类标信息,重新定义了拉普拉斯判别项,并通过学习到的稀疏保持结构正则化拉普拉斯判别项以达到既考虑判别性能又保持数据稀疏表示结构的目的.

2.1构造级联字典

假设数据样本集为X={x1,x2,…,xn},样本xi∈Rm.令X=[X1,X2,…,XK],表示所有样本一共有K个类别，此处Xi=[xi1,xi2,…,xini]∈Rm×ni表示第i类样本.假设同类样本位于一个线性子空间中,则样本可由该类的若干原子线性表出.对每一类Xi做主分量分析,其目标函数为

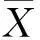
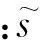
(6)上述公式的约简过程利用了PCA分解中各主分量的正交性.图1显示了级联字典D的构造过程.

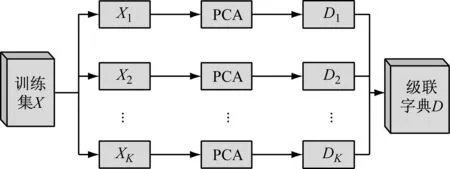
图1　级联字典的构造过程

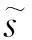
2.2构造稀疏保持正则项

级联字典D在一定程度上描述了数据的几何结构.每一个样本x的稀疏系数s显式编码了训练样本的判别信息.所以高维空间中的稀疏表示结构最好能在投影后的低维空间中得到保持,定义目标函数Js(w)如

(7)其中，si是样本xi在级联字典D下的稀疏表示系数.式(7)可整理为

(8)

其中S=[s1,s2,…,sn]，从而(7)可写成

DSXT+DSSTDT)w

(9)2.3构造拉普拉斯判别项

拉普拉斯判别的目标是使得样本投影后非局部散度尽量大而局部散度尽量小.首先定义相似度矩阵Ω=[Ωij]和差异度矩阵B=[Bij]如下

(10)

(11)其中σ是参数,通常取训练样本的标准方差.由上述定义可以看出,若两个样本距离较近且来自同一类,则其相似度较大,反之亦然;若两个样本距离较远且来自不同类别,则其差异度较大,反之亦然.故它们可以将同类样本通过投影后更加紧凑,而不同类样本投影后更加分离.

局部散度JL和非局部散度JN可表示为

(12)

(13)

其中yi=wTxi为原始数据xi经过投影后的目标数据,经过一些代数操作,式(12)可整理为

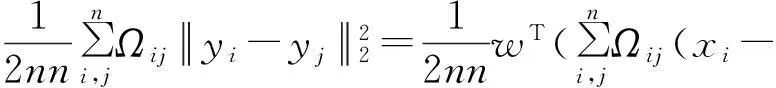
(14)

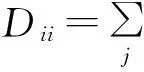
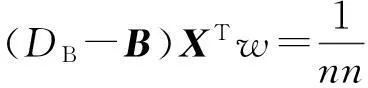
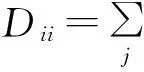
(16)2.4SPLDA算法

稀疏保持拉普拉斯判别分析(SPLDA)的目的是在寻求一个有效的判别子空间的同时保持数据的稀疏表示结构.根据2.2节,最小化稀疏保持正则项Js(w)就能保持稀疏表示结构,故SPLDA的目标函数如下

(17)

其中JN(w)和JL(w)分别是2.3节中的非局部散度和局部散度,Js(w)是2.2节中的稀疏保持项.为避免小样本问题,加入吉洪诺夫正则项wTw[15].λ1,λ2是控制分母中三项平衡的正则化参数.

经过一些代数操作,式(17)可整理为

(18)

式中： I是对应吉洪诺夫正则项的单位矩阵；M是对应稀疏保持正则项的矩阵.M=XXT-XSTDT-DSXT+DSSTDT,故SPLDA的目标函数可重写为

(19)

式(19)最终转化为求解广义特征值问题如下：

(20)

故最佳投影矩阵W=[w1,w2,…,wd]可由上述广义特征值问题中最大的d个特征值对应的特征向量组成.

综上所述,利用SPLDA算法进行人脸识别的基本步骤如下:

(1)为保证XLBXT是非奇异的,首先对原始图像进行PCA降维处理,将高维的人脸特征通过转换矩阵投影到低维的PCA子空间,并求得投影矩阵UPCA.

(2)对每类样本的训练集Xi执行PCA分解,求出级联字典D; 计算任一样本x在级联字典D下的稀疏系数s进而获得稀疏权重矩阵S;代入M=XXT-XSTDT-DSXT+DSSTDT获得矩阵M.

(3)建立类内相似度矩阵Ω和类间差异度矩阵B,并计算拉普拉斯矩阵LΩ=DΩ-Ω和LB=DB-B.

(4)求解广义特征值问题XLBXTw=η(XLΩXT+λ1I+λ2M)w, 获得初始投影矩阵U*.

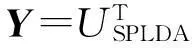
(6)利用最近邻分类器对测试图像进行分类.对每一个投影后的测试图像,比较其与投影后的训练图像间的欧式距离,并判决为与其最近的图像同类,进而通过决策的正确与否求出SPLDA算法的人脸识别率.

3实验结果与分析

为验证本文所提算法SPLDA的正确性和有效性,分别在Yale[17],ORL[18]和扩展的Yale B[19]人脸库上进行实验,实验结果与经典算法PCA, LDA, LPP，NPE和SPP进行比较.识别过程通常由以下三部分组成：① 首先计算出各种算法在同一训练样本集中相应的投影矩阵;② 将测试样本投影到所学的投影矩阵得到其在低维空间中的特征表示;③ 使用最近邻分类器对测试样本完成识别.本文的实验环境为Intel(R) Core(TM) i7-4770K,3.50GHz CPU,16.0 G内存,Windows 7 操作系统,实现算法的软件是Matlab R2013a.

Yale数据库[17]由15人组成,共165幅灰度图像,每人11幅;ORL[18]数据库共有40个人的400幅人脸图像,每人10幅;扩展Yale B[19]数据库包含38个人的2414张人脸图像,每人有大约64幅图像.这些图像包括了姿态、光照和表情的差异.为有效计算,所有图像都根据眼睛的位置进行配准,然后被缩放成大小为32×32的图像.

在本实验中,每人随机选取一半图像用于训练(Yale，ORL和扩展版Yale B每人分别随机选取6，5和32幅图像),其余图像用于测试,重复50次,最后取平均值作为识别结果.PCA和LDA没有模型参数, SPP[14]中的参数ε设为0.05,LPP和NPE中的邻域模式设为“Supervised”,权值模式设为“Cosin”. SPLDA中的参数σ取为各训练集的标准方差,而(λ1,λ2)通过10倍交叉验证从集合S={0.01, 0.02,…,1.00}中选择.对Yale, ORL及扩展Yale B相应的(λ1,λ2)分别设置为(0.94,0.25), (0.72,0.36)和(0.90,0.20).

因人脸向量空间的维数远大于训练样本的个数,SPLDA，LDA，LPP，NPE等方法都涉及PCA预处理阶段,即先将训练样本集投影到主分量生成的子空间上.由于Yale和ORL数据库规模较小,在PCA 预处理阶段保留100%的能量;而针对规模较大的Yale B 扩展数据库,为能在合理的时间内得到实验结果，在PCA 预处理阶段保留98%的能量.

特征提取算法的识别率通常随维数的大小而变化.图2显示了PCA，LDA，LPP，NPE，SPP和SPLDA在三个测试数据库上的识别率随维数的变化情况.各种特征提取算法在三个库上的最高识别率及对应方差总结在表1中.另外需要指出的是,由于LDA所对应的广义特征值问题最多只有K-1个非零特征值(K为类别数)，故其提取的特征维数上界是K-1,从图2的试验结果中也可以看到.

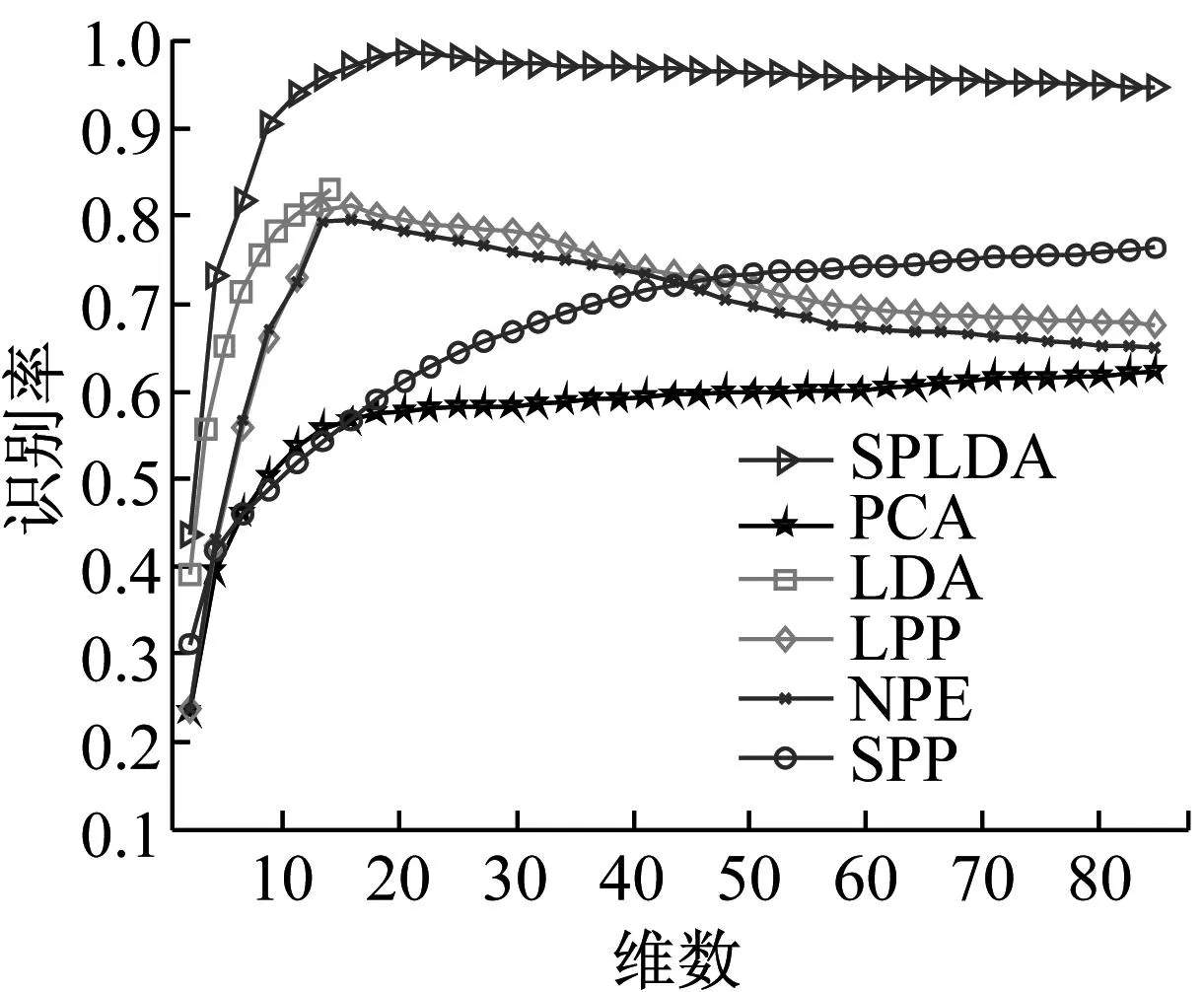
a Yale

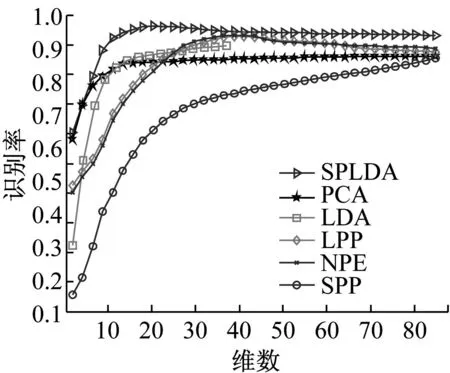
b ORL

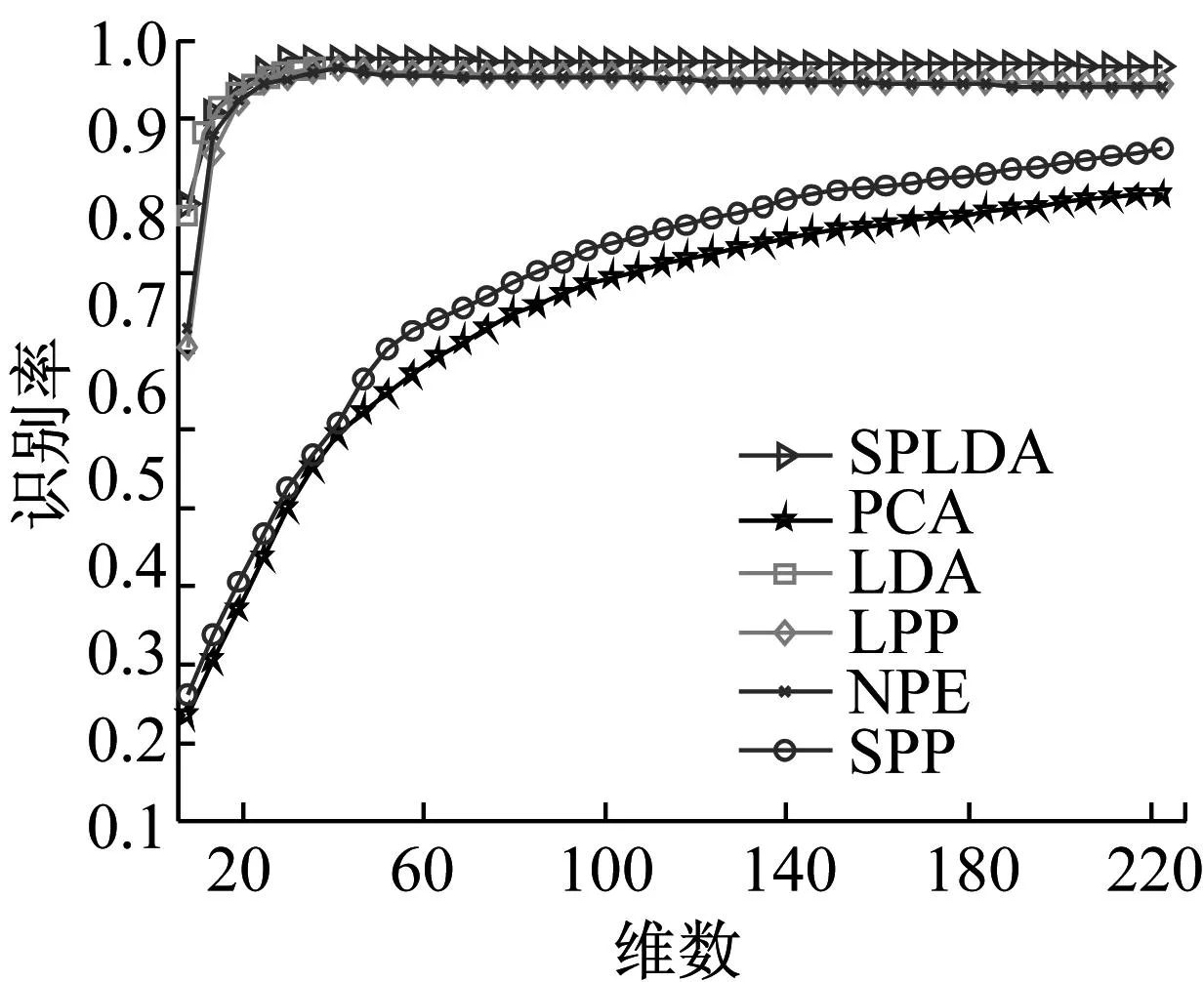
c 扩展版Yale B

算法PCALDALPPNPESPPSPLDAYale62.41(±3.83)81.32(±3.71)81.39(±2.73)81.12(±1.69)76.53(±2.58)98.27(±3.15)ORL86.26(±2.31)92.31(±2.73)92.89(±2.26)93.31(±2.34)87.04(±3.16)96.32(±3.29)扩展YaleB80.41(±2.07)96.47(±2.59)95.91(±3.68)94.71(±2.62)84.73(±2.47)97.17(±3.48)

通过图2可以看出,SPLDA的识别率比其他所有方法都高,这是因为SPLDA在寻求最优嵌入函数的同时保持了数据的稀疏表示结构;另外,SPLDA在初试阶段的识别率随维数的增加比其他方法更快,这是因为在学习稀疏表示结构和计算拉普拉斯判别项时都用到了类标信息.这表明相比于其他方法,SPLDA在一个比较低维的子空间中获得了更好的判别性能,这有利于降低计算成本及节约维数约简后的存储空间.

另外,本实验还对SPLDA和SPP学习嵌入函数的运行时间上做了比较.SPLDA和SPP在每个测试数据库上学习嵌入函数所需的平均时间总结在表2中.从实验结果看,SPLDA比SPP执行时间少的多,特别是在扩展Yale B等较大规模数据库上.这是因为SPLDA在学习稀疏表示结构时只需做K个PCA分解和n个最小二乘法,而SPP在学习稀疏表示结构时需要求解n个耗时的l1范数优化问题.

表2　SPLDA和SPP学习嵌入函数运行时间比较

最后,本文研究了SPLDA算法中吉洪诺夫正则项和稀疏保持正则项的控制参数λ1及λ2的鲁棒性问题.在Yale数据库上λ1(λ2=0.25)和λ2(λ1=0.94)对SPLDA的性能影响如图3所示.从实验结果可知，SPLDA的识别性能随λ1,λ2变化较小,所以其对正则参数λ1,λ2是鲁棒的.

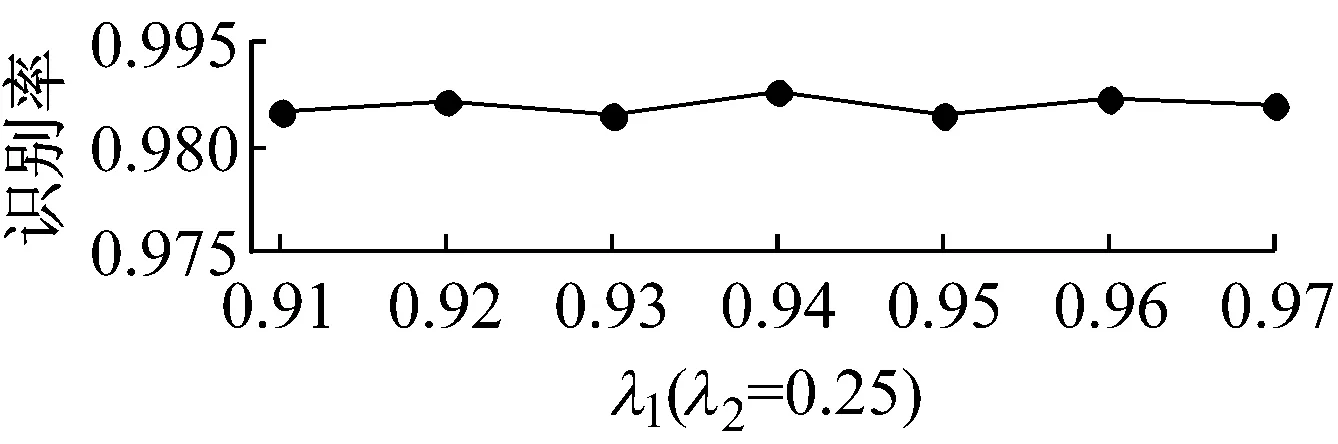
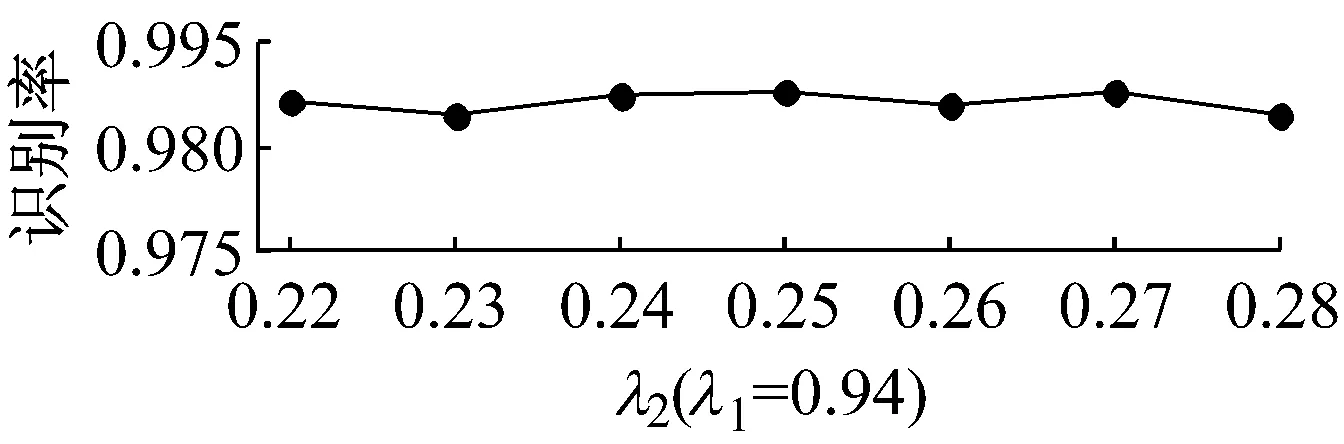
图3　在Yale数据库上参数对SPLDA识别性能的影响

4结论

提出一种基于稀疏保持拉普拉斯判别分析的特征提取算法,其目的是在寻求最佳投影矩阵的同时保持数据的稀疏表示结构.具体来讲,SPLDA首先通过逐类PCA构造级联字典,并基于该字典通过最小二乘法快速学习稀疏保持结构,然后SPLDA通过学习到的稀疏表示结构正则化拉普拉斯判别项以达到同时考虑稀疏表示结构和判别效率的目的.所提算法最终化转为一个求解广义特征值问题.在一些公共人脸数据库上的实验证明了所提算法的优越性能.

参考文献:

[1]Gupta S, Girshick R, Arbeláez P,etal. Learning rich features from RGB-D images for object detection and segmentation[C]//European Conference on Computer Vision(ECCV). Zurich: [s.n.], 2014: 345-360.

[2]Zhang W, Tang X, Yoshida T. TESC: an approach to text classification using semi-supervised clustering [J]. Knowledge-based Systems, 2015, 75:152.

[3]ZHAO Xueyi, ZHANG Zhongfei. Multimedia retrieval via deep learning to rank[J]. Signal Processing Letters, IEEE, 2015, 22(9):1487.

[4]Li C H, Ho H H, Kuo B C,etal. A semi-supervised feature extraction based on supervised and fuzzy-based linear discriminant analysis for hyperspectral image classification[J]. Journal of Applied Mathematics, 2015,9(1L):81.

[5]ZHANG D H, DING D, LI J,etal. PCA based extracting feature using fast fourier transform for facial expression recognition[C]//Transactions on Engineering Technologies.[S.l.]: Springer Netherlands, 2015: 413-424.

[6]LAI Yiqiang. Rotation moment invariant feature extraction techniques for image matching[J]. Applied Mechanics and Materials, 2015, 721:775.

[7]Jolliffe I T. Principal component analysis [M]. New York: Springer, 1986.

[8]Fukunaga K. Introduction to statistical pattern recognition [M]. 2nd ed. New York: Academic Press, 1990.

[9]Tenenbaum J, Silva V, Langford J.A global geometric framework for nonlinear dimensionality reduction[J].Science, 2000,290 (5050):2319.

[10]Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation [J]. Neural Computation, 2003,15(6): 1373.

[11]Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000,290(5500):2323.

[12]Zhao Z S, Zhang L, Zhao M,etal. Gabor face recognition by multi-channel classifier fusion of supervised kernel manifold learning [J]. Neurocomputing, 2012, 97: 398.

[13]He X, Cai D, Yan S,etal. Neighborhood preserving embedding[C]//IEEE International Conference on Computer Vision (ICCV). Beijing: IEEE, 2005:1208-1213.

[14]Qiao L, Chen S, Tan X. Sparsity preserving projections with applications to face recognition[J]. Pattern Recognition, 2010, 43(1):331.

[15]Tikhonov AN, Arsenin VY. Solution of ill-posed problems[M]. Washington D C: Winston & Sons, 1977.

[16]LOU Songjiang, ZHANG Guoyin, PAN Haiwei,etal. Supervised lapupacian discriminant analysis for small sample size problem with its application to face recognition [J]. Journal of Computer Research and Development, 2012, 49(8):1730.

[17]Belhumeur PN, Hespanha J, Kriegman D. Eigenfaces vs. fisherfaces: recognition using class specific linear projection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(7): 711.

[18]Samaria F, Harter A. Parameterisation of a stochastic model for human face identification[C]//Second IEEE Workshop on Applications of Computer Vision. Sarasota: IEEE, 1994:138-142.

[19]Lee K, Ho J, Kriegman D. Acquiring linear subspaces for face recognition under variable lighting [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5):684.

Feature Extraction with Sparsity Preserving Laplacian Discriminant Analysis

REN Yingchun1,2, WANG Zhicheng1, ZHAO Weidong1, PENG Lei3

(1. CAD Research Center, Tongji University, Shanghai 200092, China; 2. School of Mathematics, Physics and Information Engineering, Jiaxing University, Jiaxing 314001, China; 3. College of Information Engineering, Taishan Medical University, Taian 271016, China)

Abstract：Aiming at the unsupervised and time-consuming l1 norm optimization problems of the existing sparsity preserving projection, a novel fast feature extraction algorithm named sparsity preserving laplacian discriminant analysis (SPLDA) is proposed. SPLDA first creates a concatenated dictionary via class-wise principal component analysis(PCA) decompositions and learns the sparse representation structure of each sample under the dictionary using the least square method. Then SPLDA considers both the sparse representation structure and the discriminative efficiency by regularizing the Laplacian discriminant function from the learned sparse representation structure. Finally, the proposed method is transformed into a generalized eigenvalue problem. Extensive experiments on several popular face databases (Yale, Olivetti Research Laboratory(ORL) and Extended Yale B) are provided to validate the feasibility and effectiveness of the proposed algorithm.

Key words：feature extraction; sparse representation; Laplacian discriminant analysis; principal component analysis; face recognition

文献标志码：A

中图分类号：TP391

通讯作者：王志成(1975—),男,副研究员,工学博士,主要研究方向为模式识别.E-mail: zhichengwang@tongji.edu.cn

基金项目：国家自然科学基金(61103070;11301226);浙江省自然科学基金(LQ13A010017);山东省自然科学基金(ZR2015FL005)

收稿日期：2010—00—00

第一作者： 任迎春(1982—),男,博士生,主要研究方向为模式识别及计算机视觉.E-mail: renyingchun2008@163.com