粘滞阻尼墙模型的振动台实验方法

孙飞飞， 莫　刚

(1.同济大学 土木工程防灾国家重点实验室，上海 200092; 2.同济大学 土木工程学院，上海 200092)



粘滞阻尼墙模型的振动台实验方法

孙飞飞1， 莫刚2

(1.同济大学 土木工程防灾国家重点实验室，上海 200092; 2.同济大学 土木工程学院，上海 200092)

摘要：粘滞阻尼墙是一种速度相关型的阻尼器，依靠粘滞材料的剪切变形来耗能.对粘滞阻尼器进行实验加载的传统方法是采用高速作动器，对实验设备要求比较高.为了降低实验成本，利用更普及的实验设备——振动台对粘滞阻尼墙模型进行加载，提出了一种新的实验方法：实验模型中完全由粘滞阻尼墙承担水平力，没有设置其它的抗侧构件；水平力由与粘滞阻尼墙内部钢板相连的配重的惯性效应产生；配重的自重通过承重构件传递到滑轮上.同时提出了高精度的数据拟合和分析方法，可以通过计算间接得到粘滞阻尼墙的滞回曲线.设计、制作了一个小比例实验模型，通过振动台加载，取得了很好实验效果，证明了所提实验方法的正确性.最后通过理论推导，针对利用振动台加载的实验设计提出了建议方法.

关键词：粘滞阻尼墙； 实验方法； 振动台； 实验设计

粘滞阻尼墙(viscous damping wall, V D Wall)最早是日本学者Miyazaki[1]于1986年提出来，由Sumitono Contruction公司研制成功的一种可作为墙体安装在结构层间的阻尼系统，它主要由内部钢板、外部钢板及处于内外钢板之间的粘滞液体三部分构成，内部钢板固定于上层楼面，而外部钢板固定于下层楼面，并且内钢板能在其中沿平面运动[2].实际工程中往往在阻尼墙的外部设钢筋混凝土或防火材料的保护墙.地震时，楼层间的相对运动使内外钢板间产生速度差，高浓度粘滞材料产生剪切变形而形成粘滞阻尼力，进而达到消耗地震能量的目的.该粘滞阻尼墙体系首次应用于日本Shizuoka City的Sut-Building建筑[3]中，结果证明能使框架在弹性工作阶段的阻尼比达到20%～30%，显著降低了结构的动力反应.在设计和研究粘滞阻尼墙时，通常还需要采用模型实验[4-6]来确定粘滞阻尼墙的滞回曲线.传统的测试方法是将粘滞阻尼墙的外钢箱固定于地面，将内钢板与高速作动器连接，利用高速作动器进行加载[7-11].这种实验方法对实验设备要求比较高，需要刚度和强度较大的反力墙，实验时比较难以找到合适的实验装置.而在建筑结构实验中比较普及的加载设备是振动台.本文就提出了一种新的实验方法：利用振动台进行间接加载的实验方法.

1利用振动台加载的粘滞阻尼墙模型及实验方法

1.1制作实验模型

粘滞阻尼墙的构造如图1所示.本次实验的粘滞阻尼墙是由3D打印机制作的塑料墙，同样包括了外部箱体、内部塑料板和粘滞液体.墙体大小约为30 mm×100 mm×100 mm.具体尺寸如图2和图3所示.总共制作了两片墙，分别位于实验模型的两侧，如图4.粘滞阻尼墙的内平板固定于顶板两侧，外箱固定于振动台上.由于内平板与外箱并不连接，需要设置两块支撑板为顶板提供竖向支持力.为了让顶板及支撑板能够自由滑动，设置了4个滑轮减少摩擦.顶板上放置配重为顶板及其连接部分提供惯性力，振动台才能间接对实验模型进行加载.

图1　粘滞阻尼墙构造图

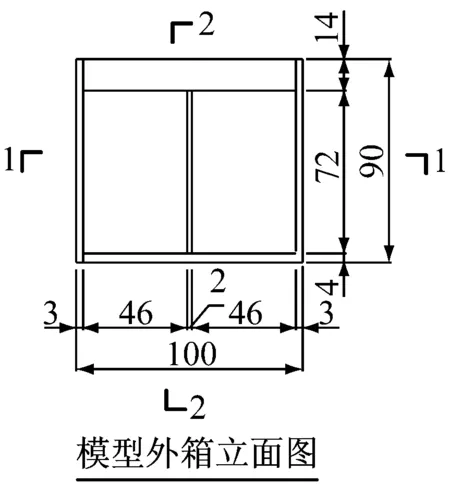
图2　粘滞阻尼墙外箱模型设计图(单位:mm)

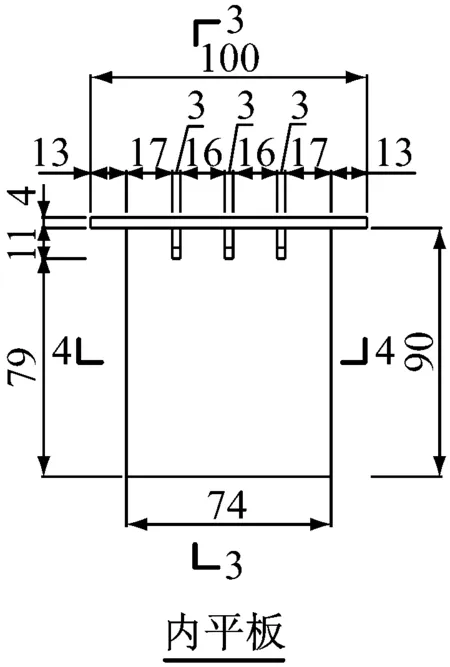
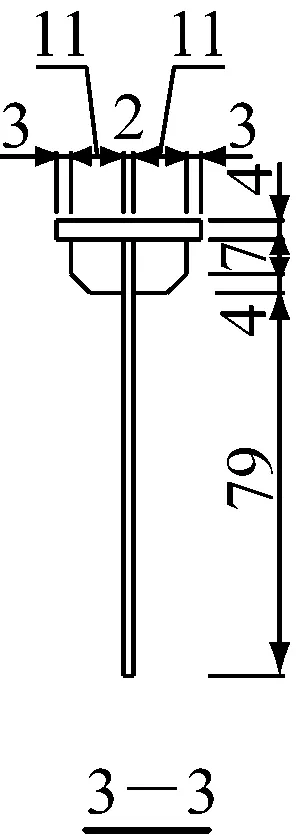
图3粘滞阻尼墙内平板模型设计图(单位:mm)

Fig.3Inside flat in V D Wall(Unit: mm)

图4　粘滞阻尼墙模型设计示意图

本实验模型的设计有如下优点：

(1) 采用两片阻尼墙和两片支撑板，保证模型在加载时的稳定性.

模型的振动方向与两片支撑板平行，在模型的顶板上需要加上足够的配重，振动台才能靠惯性力让阻尼墙中的粘滞液体剪切变形来耗能.以两片相同的粘滞阻尼墙分别处于顶板的两侧可以保证实验中顶板两侧受到的阻尼力是几乎相等的，避免了顶板发生扭转或侧移.用两片支撑板不仅能够提供支持力，还能保证加载时顶板不会向某侧倾斜.

(2) 模型没有抗侧力构件，模型测量和数据分析比较简单.

本模型没有设置柱或墙作为抗侧力构件，仅用支撑板为顶板提供竖向支持力.为了减小水平方向滑动的摩擦力，模型用了4个滑轮来支撑支撑板.这种构造方式能去除抗侧力构件的内力影响，不仅减少了实验测量的数据，还让实验数据的处理变得简单.

1.2实验测量方法

由于模型的制作具有前文提到的一些优点，因此实验的测量也变得非常简单.仅仅需要同时测量顶板以及振动台的位移和顶板上的配重.实验采用激光位移计测量位移，采点周期为1 ms，利用电子称测量配重.阻尼墙模型的最大变形量为10 mm，为了观察到明显的变形且不超过最大变形量，在模型上加上了25 kg的配重.振动台按正弦波加载.

1.3数据处理方法

根据受迫振动的方程式

(1)

可得阻尼力为

(2)

即

(3)

显然，粘滞阻尼墙内平板与外箱之间的相对位移为

(4)

式中:y为对位移；yg为振动台位移；Fd为粘滞阻尼力；m为配重；yp为顶板的振动位移.

实验测得的曲线都是位移曲线，为了利用式(3)求得粘滞阻尼墙的阻尼力，需要对位移求二次导数.直接对实验曲线进行数值求导会带来较大误差.可以根据实验测得的曲线特征，先对实验测得的位移曲线进行拟合，再进行求导.

2实验数据处理结果

鉴于篇幅限制，本文给出如下两种加载工况下的数据处理结果，以说明数据处理的合理性：① 振动台加载频率为0.8 Hz，位移幅值为45 mm；② 振动台加载频率为1.2 Hz，位移幅值为40 mm.

实验得到的位移曲线是比较标准的正弦曲线，因此用正弦曲线对实验结果进行拟合.拟合得到的正弦曲线表达式如表1所示.从图5中可以看出，实验曲线与拟合曲线吻合得相当好，可以认为拟合曲线包含了实验曲线的主要特点，能够反映实验的真实情况.利用拟合曲线对数据进行处理是非常重要的，从图6和图7可以分别看出拟合对求得滞回曲线两个重要参数的影响.图6中，根据实验数据直接得到的相对位移曲线在很多地方都不光滑，在最大值处更是有很多噪声干扰，拟合曲线得到的相对位移就是一条标准的正弦曲线.图7中，直接对实验数据求二次导数会将实验数据中的噪声放大，得到的二次导数曲线波动很大，用这样的曲线作出的滞回曲线会掩盖构件真实的反应，得不到想要的结果.用拟合曲线求导就避免了噪声的干扰，能得到标准的正弦曲线.

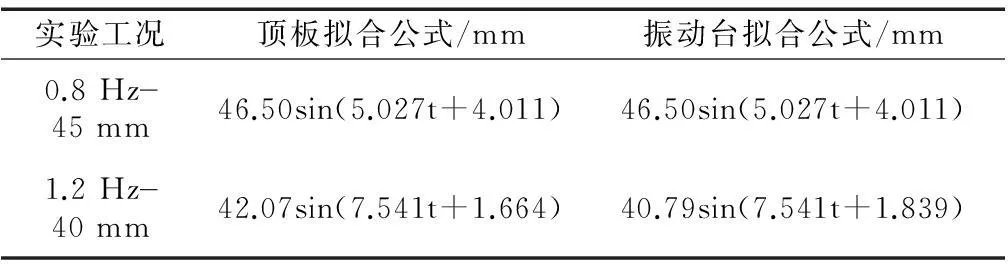
表1　根据实验得到的拟合曲线公式

a 0.8 Hz—45 mm时顶板的位移曲线

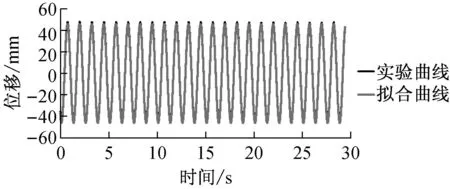
b 0.8 Hz—45 mm时振动台的位移曲线

c 1.2 Hz—40 mm时顶板的位移曲线

d 1.2 Hz—40 mm时振动台的位移曲线

图8是两个工况下通过拟合曲线得到的粘滞阻尼墙的滞回曲线.曲线是标准的椭圆，清楚地反应了粘滞阻尼墙的恢复力特性.在对粘滞阻尼墙恢复力模型的研究中，通常会用到滞回曲线上的某些特殊点.利用图8的滞回曲线来选取特殊点就比较容易而且相当准确.

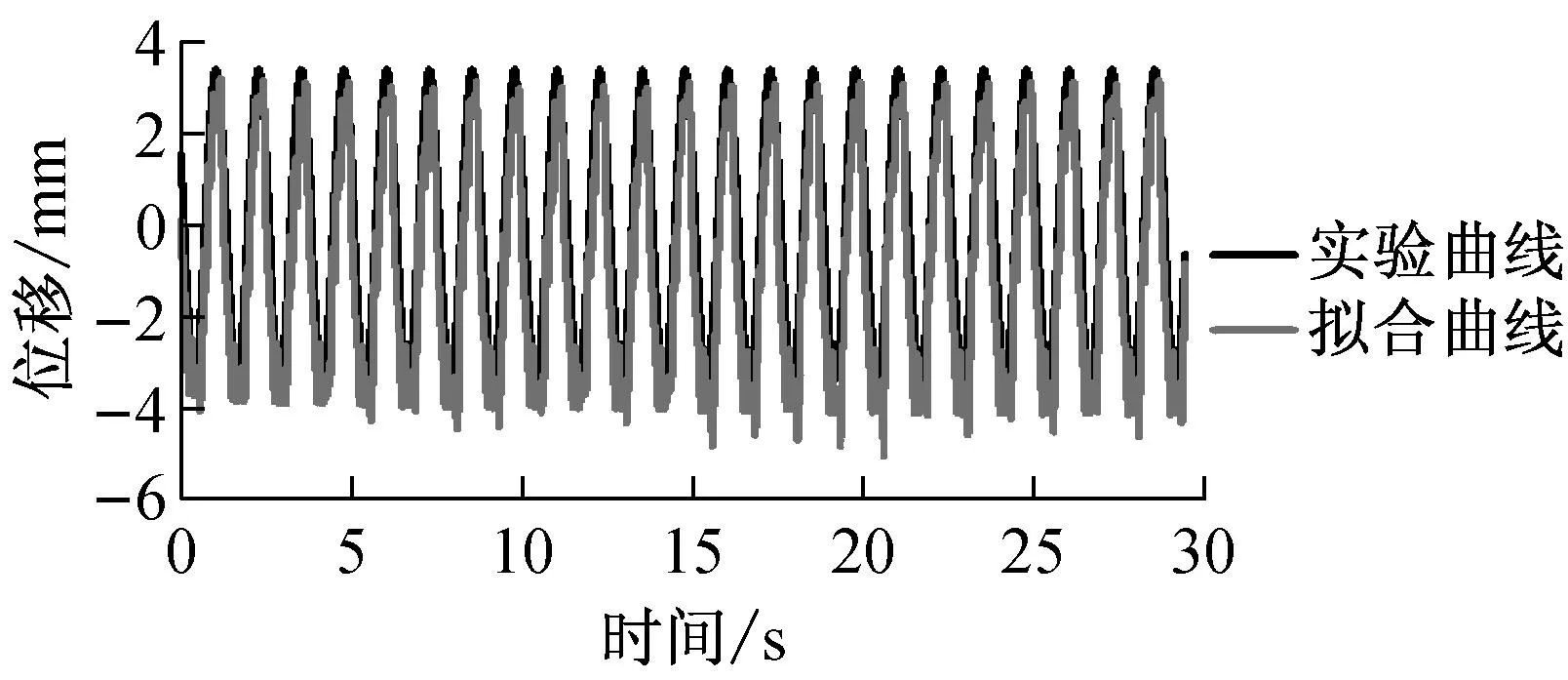
图6　0.8 Hz—45 mm时的相对位移曲线

图7　0.8 Hz—45 mm时顶板曲线二次导数

a 0.8 Hz—45 mm

b 1.2 Hz—40 mm

3振动台实验设计建议方法

通过实验得到的滞回曲线可以确定粘滞阻尼墙的弹性刚度和粘滞系数，得到公式如下：

(5)

代入式(1)可得

(6)

即

(7)

(8)

(9)

(10)

通过式(9)即可预测所加配重和所输入的正弦波将能达到的相对位移.

利用本文的试验方法对粘滞阻尼墙的恢复力曲线进行检验，实验设计可按下述步骤进行：

(1) 将粘滞阻尼墙的恢复力的设计公式代入式(1)，得到振动方程.粘滞阻尼墙的恢复力公式可能有如下三种情况：粘滞阻尼墙的恢复力公式是如式(5)的形式，则直接代入式(1)得到振动方程；恢复力公式只给出了线性的粘滞力部分，可将弹性刚度取得足够小再代入式(1)得到振动方程；恢复力公式只给出了非线性的粘滞力部分，可以根据恢复力曲线包围的面积相等的原则等效为线性公式，再将弹性刚度取得足够小再代入式(1)得到振动方程.

(2) 确定实验中粘滞阻尼墙需要达到的相对位移值.

(3) 通过式(9)综合考虑振动台位移幅值和粘滞阻尼墙顶部的配重质量，来达到需要的相对位移值.

(4) 将选择的配重加到实验模型上，再输入正弦波.为了避免正弦波输入时产生的瞬态振动过大，振动台加载可以采位移幅值逐渐增大的正弦波.

以本文的两个实验结果做算例,两个实验工况分别得到的粘滞系数和弹性刚度如表2所示.

本实验得到的恢复力公式如式(5)，能直接代入式(1)得到振动方程，可直接按式(9)计算相对位移幅值.确定试验时两个加载频率下粘滞阻尼墙的相对位移为10 mm，根据式(9)可以得到振动台的幅值和配重的关系曲线，如图9所示.

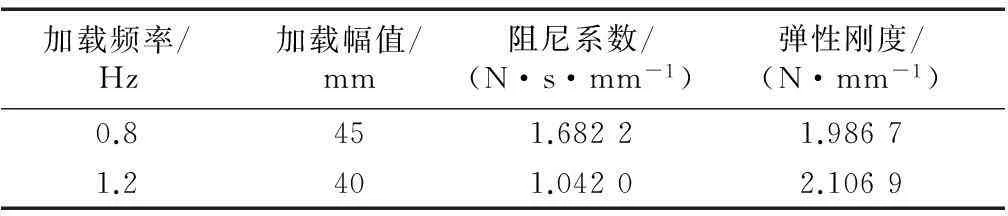
表2　实验得到的阻尼系数及弹性刚度

图9　各工况下的配重—振动台幅值曲线

为了达到相对位移为10 mm，根据图9得到的曲线可以选择：加载频率为0.8 Hz时，选取配重55 kg，振动台幅值为61 mm；加载频率为1.2 Hz时，选取配重为35 kg，振动台幅值为40 mm.

实际工程中通常也需要对工程需要用到的粘滞阻尼墙进行实验检测，某粘滞阻尼墙的型号如下：

VDF-NL×600×80，阻尼系数为1 100 kN·s·m-1，阻尼指数为0.3，设计行程为80 mm，结构基本频率为0.3 Hz.

由于给出的粘滞阻尼墙的阻尼力是非线性的，先根据实验工况滞回曲线包围面积相等等效为线性公式.得到的等效阻尼系数为4 840 kN·s·m-1，等效曲线与原曲线的对比如图10.该阻尼墙没有给出动态的弹性刚度，只需要把刚度取得足够小，取为1×10-6kN·m-1.将该阻尼墙的参数代入式(9)，就可以得到振动台加载的位移幅值与附加配重之间的关系曲线，如图11.

图10　原滞回曲线与等效曲线

从图11中可以看出，实际工程应用的粘滞阻尼墙吨位较大，加载到预计相对位移幅值需要较大的配重和振动台位移幅值.一般的实验室无法满足这一条件，需要将实验方案做一个改进：将粘滞阻尼墙的内钢板与弹性刚杆相连，弹性刚杆与实验室的反力墙连接，外钢箱与振动台台面连接，并在弹性刚杆上贴上若干应变片.直接输入需要测试的位移幅值及频率，就可以通过应变片的读数计算得到粘滞阻尼墙的阻尼力，装置如图12所示.

图11　实际粘滞阻尼墙的配重—振动台幅值曲线

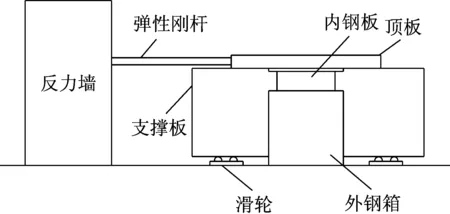
图12　改进实验装置示意图

改进前后的实验装置各有一些优缺点，需要根据实际情况进行选择.

改进前的实验装置优点是不需要使用反力架，实验装置简单，数据测量容易；内钢板自由，与实际工程中的情况更接近.缺点是不能测试大吨位的粘滞阻尼墙.

改进的实验装置优点是能测试大吨位的粘滞阻尼墙.缺点是需要使用反力墙，让实验装置更复杂；在模型顶板上也需要加上一些配重，保证顶板在加载过程中不会向上旋转翘起；对实验加载的控制要求比较高，不能让外钢箱与内钢板相碰，否则容易损坏实验模型或设备，这与实际结构中的情况有些出入.

4结论

(1) 利用振动台间接加载来测试粘滞阻尼墙的滞回曲线同样能够得到很好的实验结果，且相比于传统的采用高速作动器加载的方法，振动台实验对实验设备要求低，更容易找到合适的实验装置.

(2) 实验模型中不包括抗侧力构件可以简化实验数据的测量和处理，仅测量模型顶板和振动台的位移即可.

(3) 实验数据处理时根据实验曲线的特点对曲线进行拟合，排除随机干扰带来的求导等影响，能够得到光滑且准确的滞回曲线.

(4) 根据本文提出的实验设计的建议方法，能够根据需求的相对位移幅值，很方便地通过公式确定粘滞阻尼墙的配重以及振动台的加载位移幅值.

(5) 采用附加配重的振动台实验方法测试实际工程中的粘滞阻尼墙，需要过大的配重和振动台幅值.一般的实验室难以满足，采用改进方法能够有效地利用振动台的加载能力，实现对实际工程使用的粘滞阻尼墙的实验验证.

(6) 改进前后的实验装置各有优缺点，需要根据实际情况选择合理的加载装置.

参考文献:

[1]Miyazaki M, Arima F, Kidata Y,etal. Earthquake response control design of buildings using viscous damping walls[C]∥Proceedings of first East Asia Pacific Conference. Bangkok: [s.n], 1986: 1882-1891.

[2]周云. 粘滞阻尼减震结构设计[M]. 武汉：武汉理工大学出版社, 2006.

ZHOU Yun. Structural design with viscous damper[M]. Wuhan: Wuhan University of Technology Press, 2006.

[3]Miyazaki M, Mitsusaka Y. Design of buildings with 20% or greater damping[C]∥Proc of Tenth World Conference on Earthquake Engineering. Rotterdam: Balkema, 1992:4143-4148.

[4]谭在树,钱稼茹. 钢筋混凝土框架用粘滞阻尼墙减震研究[J]. 建筑结构学报, 1998(2):50.

TAN Zaishu, QIAN Jiaru. Research of reinforced concrete frame with viscous damping wall[J]. Journal of Building Structures, 1998(2):50.

[5]郑正昌,森高英夫,下田郁夫,等. 鹿儿岛机场候机楼抗震补强——增设粘滞阻尼墙的结构三维弹塑性分析[J]. 建筑结构,2000,30(6):19.

ZHENG Zhengchang, Hideo Moritaka, IKuo Shimoda,etal. Anti-seismic strengthening of the Kagoshima Airport terminal building[J]. Building Structure, 2000,30(6): 19.

[6]夏冬平,张志强,李爱群,等. 新型黏滞阻尼墙动力性能试验研究[J]. 建筑结构,2013,43(13):46.

XIA Dongping，ZHANG Zhiqiang，LI Aiqun,etal. Experimental study on dynamic performance of a new viscous damping wall[J]. Building Structure, 2013, 43(13):46.

[7]欧谨. 粘滞阻尼墙结构的减振理论分析和试验研究[D]. 南京:东南大学, 2006.

OU Jin. Theoritical and experimental research on structures with viscous damping wall[D]. Nanjing: Southeast University, 2006.

[8]闫锋. 粘滞阻尼墙耗能减振结构的试验研究和理论分析[D]. 上海:同济大学, 2004.

YAN Feng. Experimental and theoritical research on structures with viscous damping wall[D]. Shanghai: Tongji University, 2004.

[9]章征涛. 粘滞阻尼墙及其动力性能的实验研究[D]. 南京:南京工业大学, 2003.

ZHANG Zhengtao. Experimental study on the dynamic behaviors of viscous damping wall[D]. Nanjing: Nanjing Tech University, 2003.

[10]梁沙河. 新型变阻尼系数粘滞阻尼器的试验与分析研究[D].南京:东南大学, 2010.

LIANG Shahe. Experimental and analytical study of a new type controllable damping coefficient viscous damper[D]. Nanjing: Southeast University,2010.

[11]陈威, 粘滞阻尼器的理论和实验研究[D]. 武汉:华中科技大学,2012.

CHEN Wei. Theoretical and experimental researches on a viscous damper[D]. Wuhan: Huazhong University of Science and Technology, 2012.

Experimental Method on Viscous Damping Wall by Shaking Table Test

SUN Feifei1， MO Gang2

(1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 2. College of Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract：Viscous damping wall is a kind of velocity dependent damper, and relies on shear deformation of viscous material to dissipate energy. The traditional experimental method of loading for the viscous damping wall is to adopt high-speed actuator, demand of which is much high. In order to reduce the cost of the experiment, a new experimental method is proposed, that the viscous damping wall is loaded by a shaking table, which is more common. In the experimental model, the horizontal force is totally resisted by the viscous damping wall without additional lateral resisting members; the horizontal force is produced by the inertial effect of a balance weight installed upon the inner steel plate of the viscous damping wall; the self-weight of the balance weight is transferred to complimentary bearing members by rollers. Meanwhile, a datum fitting and processing method of high accuracy is proposed to acquire indirectly the hysteretic curve of the viscous damping wall. A small scaled model was designed, made and tested, showing satisfactory results, validating the accuracy of the proposed experimental method. Finally, design recommendations were given for the proposed experimental method with the derived formulae of dynamics.

Key words：viscous damping wall; experimental method; shaking table; experimental design

文献标志码：A

中图分类号：TU317.1; TU391

基金项目：上海市教委科研创新重点项目(14zz035)

收稿日期：2015—05—04

第一作者： 孙飞飞(1971—)，男，工学博士，教授,主要研究方向为多高层钢、钢-混凝土组合结构抗震分析和设计理论.

E-mail: ffsun@tongji.edu.cn.