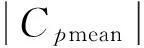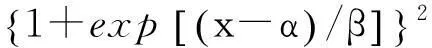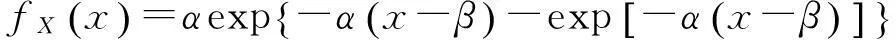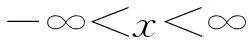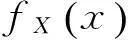典型屋顶太阳能光伏板风压实测研究

余香林， 董　锐， 王守强

(1. 同济大学 土木工程学院， 上海 200092； 2. 福州大学 土木工程学院， 福建 福州 350108；3. 同济大学 土木工程防灾国家重点实验室， 上海 200092)



典型屋顶太阳能光伏板风压实测研究

余香林1， 董锐2,3， 王守强3

(1. 同济大学 土木工程学院， 上海 200092； 2. 福州大学 土木工程学院， 福建 福州 350108；3. 同济大学 土木工程防灾国家重点实验室， 上海 200092)

摘要：对一栋多功能低层建筑平屋顶上的太阳能光伏板进行风压实测，根据风压时程特性选择适当的概率密度函数对各测点的风压系数进行非线性回归分析.运用6种概率密度函数对各测点的均值和极值(正极大值和负极小值)风压系数时程以及面积平均后的极值风压系数时程进行数值拟合，比较不同概率分布的拟合效果.回归分析结果表明：均值风压系数的概率分布近似无偏分布，t分布的拟合效果最好，其次是Logistic分布、正态分布、极值I型分布；负压极小值和正压极大值风压系数的概率分布分别为左偏分布和右偏分布，极值I型分布的拟合效果最好，其次是Lognormal分布和Gamma分布，而正态分布的拟合效果最差；最不利风压系数由极值负风压控制，即光伏板的风力由吸力主导；经面积平均后的最不利风压系数建议取值-2.3.

关键词：平屋顶； 太阳能光伏板； 原型试验； 风压系数； 极值分布

屋顶太阳能光伏板在住宅和办公建筑中日益兴起.作用于光伏板上的风压具有很强的脉动性和持续性，其风压系数极值和均值的概率分布是确定工程设计用风压系数大小的基础.普通房屋结构风压时程的概率分布已有不少学者进行过研究，且将风压系数编入了相关荷载规范[1-3].Holmes等[4]运用极值I型分布和广义极值分布对风压系数极值进行了拟合，发现具有较小正形状参数的广义极值分布拟合效果最好.Tieleman等[5]用三参数Gamma分布很好地拟合了偏度较小的风压系数时程.陶玲等[6]得出低矮房屋风压时程的概率分布与偏度有关，偏度增大时分别接近对数正态分布、广义极值分布，而面积平均后的风压时程与对数正态分布、Gamma分布和广义极值分布都吻合较好.由于现场实测难度较大，屋顶太阳能光伏板的风压分布规律研究一般通过风洞试验进行.操金鑫等[7]对平屋顶光伏板的净风压系数进行了风洞试验，结果表明单排电池板的最不利负风压系数远大于多排布置的情况，且随电池板倾角和排距的增大而增大.Stathopoulos等[8]通过风洞试验得出光伏板最不利风压系数由负压主导，并建议面积平均后的最大净风压系数取-1.7.

尽管日本规范[9]对作用于光伏板上的风荷载作了明确规定，但国内荷载规范[2]并无此类规定.由于不同地区的光伏板支撑系统和布局形式存在不同，导致其风荷载分布也存在区别.鉴于此，有必要对其他地区光伏板的风压分布进行研究，以便保证结构的设计安全.风洞试验、现场实测和CFD数值模拟是结构抗风研究的三种重要手段，其中现场实测是目前公认的相对最准确的研究方法.本文采用现场原型试验对某典型太阳能光伏板风压分布进行了研究，并从统计学和结构抗风设计可靠性的角度分析了其风压分布规律和风压系数的取值标准，得到了许多有意义的结论，可为我国工程设计和相关规范的制定提供借鉴和参考.

1试验概况

本试验的研究对象是某低矮建筑平屋顶上的太阳能光伏板，距离室外地面的高度为12 m，沿屋顶纵向排布.为充分吸收太阳能，光伏板与平屋顶的夹角为25°.为使现场实测数据具有代表性，取靠近山墙一侧的6排4列共计24小块光伏板(上下两大块)作为观测对象，太阳能光伏板试验原型如图1所示.该低矮建筑位于房屋较稀疏的郊区，场地类别为B类[2].

图1　屋顶太阳能光伏板实物图

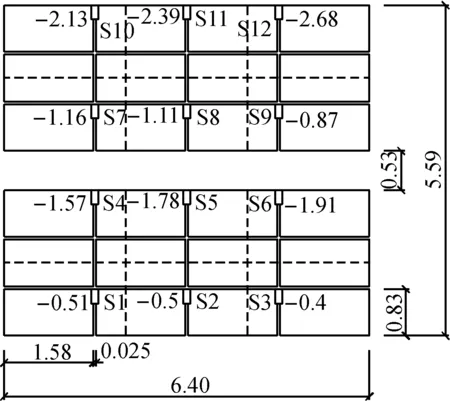
在24块光伏板上布置12个风压传感器，每块光伏板的面积均为1.3 m2(1.58 m×0.83 m).在光伏板顶部靠左位置安装型号85 000超声风速仪.光伏板尺寸及风压传感器测点布置如图2所示.

风压传感器测得的风压为净风压，即正负压差.光伏板迎风面和背风面均设有测压孔，通过测量正反面的压差，将测得的净风压数据传输至基于LabVIEW2012的数据采集系统中.传感器在光伏板上的布置如图3所示.

图2　太阳能电板传感器布置图(单位：m)

图3　风压传感器布置图

超声风速仪可测得实时风速大小和风向.因太阳能光伏板具有25°倾角，且风速仪布置在光伏板顶部檐口处；此外，风速仪的总高度为0.347 m，安装深度为0.114 m，故风速仪探头距离屋顶表面的竖直高度为5.59×sin25°+0.347-0.114=2.6 m.因此，风速仪所测风速和风向受建筑物干扰影响很小，可以代表来流风速和风向.规定北风(自北朝南吹的风) 为0°风，东风 (自东向西吹的风) 为90°风，沿顺时针方向变化时风向角逐渐增大，变化范围在0°～360°之间.风速仪实物图和俯视图见如图4和图5.

图4　型号85 000超声风速仪实物图

图5型号85 000超声风速仪俯视图

Fig.5Top view of Model 85 000 Ultrasonic Anemometer

风速、风向及风压等试验数据的采样频率为100 Hz，每个样本的采样持时为15 min，样本容量为90 000，样本数量共计501个.为防止灰尘、雨水等渗入风速仪和风压传感器的测压孔中，每次采集数据前，均留有5 min的试验准备时间，用来检查各测量仪器及线路板是否正常工作.

2光伏板风压系数分析

因单个样本数据量较大(90 000×14=1.26×106)，为排除外界环境等对实测风压和风速造成的干扰，运用滑动平均法对数据进行平滑处理(滑动平均窗口为50)，再运用低通滤波器对高频成分进行滤波处理，截止频率取15Hz.风压系数的计算公式为

(3)

2.1平均风压系数

平均风压系数的概率分布近似对称分布，故采用正态分布，t分布和Logistic分布拟合.

2.1.1正态分布

正态分布属无偏分布，其概率密度函数(PDF)和相应的累积分布函数(CDF)分别为[10]

-∞

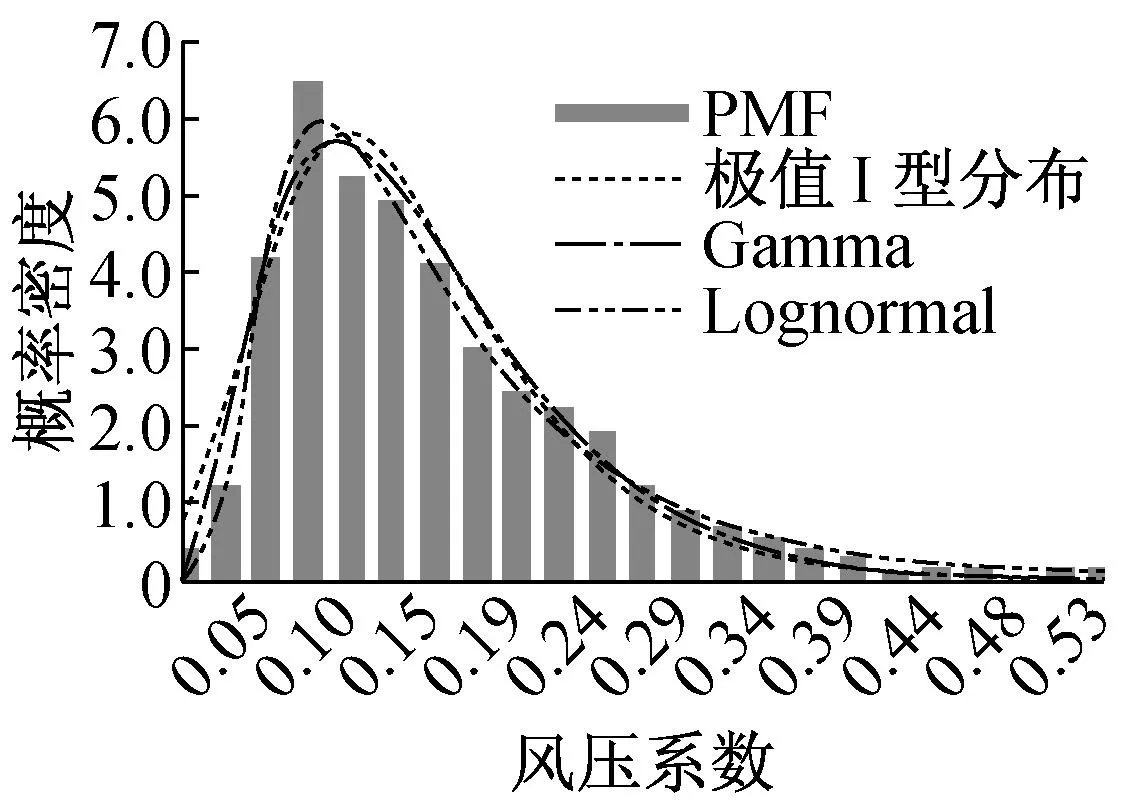
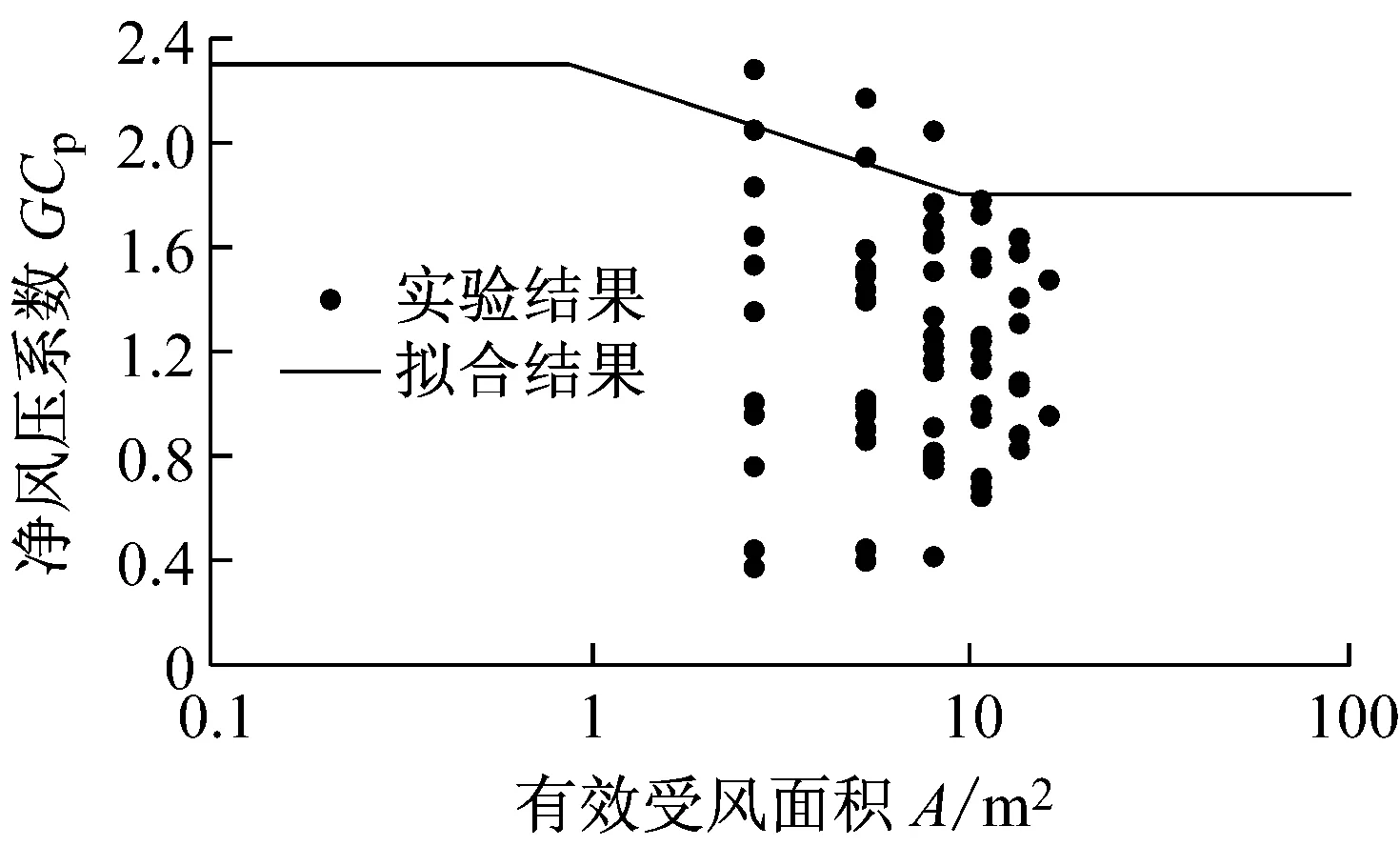
(4)

(5)

式中：σX和μX表示随机变量X的标准差和均值.

正态分布的均值净风压系数CPmean参数回归分析见表1.取双侧2.5%分位点对应的风压系数作为该测点的平均净风压系数.

表1　正态分布的平均风压系数CPmean参数分析

2.1.2t分布

t分布属于抽样分布，具有厚尾特性.当样本容量足够大时，t分布近似于正态分布.因CPmean的均值不为0(接近于0)，故用三参数t分布进行回归分析.其PDF和CDF分别为[11]

(6)

(7)

式中:Γ为Gamma函数；a为位置参数;b为尺度参数;c为自由度数.t分布的均值净风压系数CPmean参数回归分析见表2.表中，R2为拉入合度.

表2　t分布的平均风压系数CPmean参数分析

由表2知，每块光伏板上排测点(S10, S11, S12和S4, S5, S6)的CPmean的均值在左侧2.5%分位点最小(绝对值最大)，分别为-0.98和-1.53.

2.1.3Logistic分布

Logistic分布属于增长型分布，亦具有厚尾特性.其PDF和CDF分别为[11]

-∞

(8)

(9)

式中:α是位置参数，β是尺度参数.Logistic分布的CDF称为Logistic函数，且通常用于Logistic回归分析中.Logistic分布的均值净风压系数CPmean参数回归分析见表3.

由表3可知，双侧2.5%分位点对应的CPmean的绝对值比正态分布情况下的绝对值稍大，而比t分布情况下的绝对值小很多，表明Logistic分布的厚尾程度介于正态分布和t分布之间.均值风压系数CPmean拟合度对比如图6所示.

由图6知，t分布的拟合度最高，其次是Logistic分布和正态分布，而极值I型分布的拟合度最低.

2.2极值风压系数

极值风压系数分为正极大值CPmax和负极小值CPmin两种.根据极值风压的分布特点，选取常见的概率密度函数(极值I型分布, Gamma分布, 对数正态分布, 正态分布)对各测点的极值风压系数进行参数回归分析.

图6　均值风压系数CPmean的拟合度对比

2.2.1极值I型分布

通过分析各测点极值风压系数的概率质量函数(PMF, 用直方图表示)及统计量(见表4)可知，CPmax为右偏分布，CPmin为左偏分布(S7测点例外).

表4　极值风压系数的统计量

极值I型(Gumbel)分布适用于支撑集为R的右偏分布(偏度为1.14).其PDF和CDF分别 为[10]

(10)

(11)

式中：α是尺度参数，且α>0；β是对应于概率密度最大值的变量X的众值.α，β用X的均值和标准差表示为

(12)

图7　左偏分布的模型变换

通过对极值净风压系数CPmax和CPmin进行参数回归分析可知，顶部整块光伏板上排测点(S10, S11, S12)的CPmax的均值最大，为0.4.每大块光伏板顶排测点(S10, S11, S12和S4, S5, S6) 的CPmin均值的绝对值最大，分别为1.75和2.4.

2.2.2Gamma分布

(13)

(14)

(15)

对于左偏分布且x<0时，令y=-x>0，可将模型对称变换为右偏分布.

通过对极值净风压系数CPmax和CPmin进行参数回归分析可知，顶部整块光伏板上排测点(S10, S11, S12)的CPmax的均值最大，为0.45.每大块光伏板顶排测点(S10, S11, S12和S4, S5, S6) 的CPmin的均值的绝对值最大，分别为2.07和2.75.

2.2.3Lognormal分布

两参数Lognormal分布(即对数正态分布)的随机变量X的自然对数InX服从正态分布，适用于右偏分布.其随机变量X的PDF和CDF分别为[10]

0

(16)

(17)

偏度为

(18)

式中：λX是位置参数；ζX是尺度参数.λX和ζX可用X的均值和标准差表示为

(19)

通过对极值净风压系数CPmax和CPmin进行参数回归分析可知，顶排整块光伏板上排测点(S10, S11, S12)的CPmax的均值最大，为0.62.每大块光伏板顶排测点(S10, S11, S12和S4, S5, S6)的CPmin的绝对值最大，分别为-3.54和-2.97，均大于极值I型分布和Gamma分布对应的数值，这是由Lognormal分布的厚尾特性引起的.极值风压系数的拟合度对比如图8和图9所示.

由图8和图9知，Lognormal,Gamma和极值I型分布的拟合度均较高，正态分布的拟合度最低.

对上下两块光伏板的各测点极值风压系数时程进行实时平均，得到面积平均后的正极大值和负极小值风压系数.各种分布的面积平均后极值风压系数拟合度对比如表5所示.概率密度和面积平均后的概率质量(直方图) 比较如图10～图13所示.

图8　正极大值风压系数CPmax的拟合度对比

图9　负极小值风压系数CPmin的拟合度对比

表5　各种分布的面积平均后极值风压系数拟合度对比

图10　面积平均后顶部光伏板的CPmax的概率密度对比

Fig.10Comparison of probability density for area-averaged maximum pressure coefficientCPmaxof top PV panels

图11　面积平均后底部光伏板的CPmax的概率密度对比

Fig.11Comparison of probability density for area-averaged maximum pressure coefficientCPmaxof bottom PV panels

图12　面积平均后顶部光伏板的CPmin的概率密度对比

Fig.12Comparison of probability density for area-averaged minimum pressure coefficientCPminof top PV panels

Fig.13Comparison of probability density for area-averaged minimum pressure coefficientCPminof bottom PV panels

由表5可知，除了顶部整块光伏板的负极小值风压系数的拟合度较低外，其他极值风压系数的拟合度均较高.顶部光伏板负极小值风压系数拟合度偏低是因S7测点的分布为极值I型分布 (拟合度为93%，运用正态分布的拟合度为86%，概率密度和概率质量如图14所示)，且CPmin有正有负，而Gamma分布和Lognormal分布仅适用于自变量X均为正数或均为负数(经Y=-X的对称变换后，将Y作为新的自变量即为正数)的情况，故不适于用Gamma分布和Lognormal分布拟合.

图14　测点S7负极小值风压系数CPmin的概率密度对比

Fig.14Comparison of probability density for negative minimum peak pressure coefficientCPminof S7

3结果分析

S7的负极小值风压系数不宜使用Lognormal分布和Gamma分布拟合，且面积平均后的风压系数拟合度较极值I型分布更低，故从概率密度函数的整体拟合效果来看，极值风压系数时程最适合用极值I型分布拟合，而均值净风压系数最适合用t分布.基于这两种分布的各测点风压系数分析结果如表6所示.

表6　各测点净风压系数分析结果

由表6可知，各测点的最大净风压系数(绝对值最大)由负极小值净风压系数控制，且均小于0，表明作用于光伏板上的风力以吸力为主.因12个风压测点均匀分布在24小块光伏板的典型位置处，为使每块从属面积均包含1个测点，故等面积划分成12块.各测点的负极小值净风压系数及从属面积划分如图15所示.

图15　各测点负极小值净风压系数及从属面积划分

取各测点风压系数的实测值乘以对应的从属面积进行加权平均，得到整块光伏板上的风压系数.面积A平均后的净风压系数CP用下列公式计算[13]

(20)

则上式简化为

(21)

故顶部和底部整块光伏板的风压系数分别为

面积平均后的顶部和底部半块光伏板的风压系数分布如图16所示.

由图16和计算结果可知，每块光伏板上半部分的风压系数均比下半部分大，且顶部光伏板的风压系数大于底部光伏板的风压系数.

将各个测点风压系数对应的从属面积进行加权平均后求得的净风压系数进行线性回归分析，且超越概率取5%，可得出如图17所示的设计用三折线净风压系数图.当有效受风面积为0.1 m2～0.9 m2时，最不利净风压系数为-2.3.故平屋顶太阳能光伏板倾角为25°时，建议荷载规范对光伏板净风压系数取值为-2.3.

图16　净风压系数分布图

图17　太阳能光伏板净风压系数建议值

4结论

对作用于低层建筑平屋顶太阳能光伏板上的风压和风速时程进行现场实测，合理运用常见的概率密度函数对风压时程分布进行非线性回归分析，比较选取最适合风压分布规律的分布函数，提出规范化的净风压系数分布模型，得出以下结论：

(1)极值风压系数符合极值I型分布，且Lognormal分布和Gamma分布的拟合效果均较好.

(2)均值风压系数时程近似无偏分布，且具有厚尾性质，故t分布的拟合效果非常好.

(3)最不利风压由负压极小值控制，表明作用于光伏板上的风压由吸力主导，且最不利风压系数均出现在每块光伏板的上部，这是由于上下两块光伏板之间的空隙较大，且顶部光伏板上半部分位于自由风檐口处导致产生更大的吸力.底部光伏板因距离平屋顶檐口较远，故所受平均吸力明显小于顶部光伏板.

(4)顶部整块光伏板的净风压系数明显大于底部整块光伏板的净风压系数.建议取最不利风压系数(即体型系数) 作为设计参考，经面积平均后的最不利风压系数取值为-2.3.

参考文献:

[1]American Society of Civil Engineers. ASCE/SEI 7-10 Minimum design loads for buildings and other structures[S]. Reston: American Society of Civil Engineers, 2010.

[2]中华人民共和国住房和城乡建设部. GB50009-2012 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB50009-2012 Load code for the design of building structures[S]. Beijing: China Architecture & Building Press, 2012.

[3]International Code Council (ICC). 2012 International building code[S]. Country Club Hills: ICC, 2011.

[4]Holmes J D, Cochran L S. Probability distributions of extreme pressure coefficients [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91: 893.

[5]Tieleman H W, Ge Z F, Haji M R. Theoretically estimated peak wind loads [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95: 113.

[6]陶玲, 黄鹏, 顾明,等. 低矮房屋风压时程的概率分布 [J]. 同济大学学报: 自然科学版, 2013, 41 (1): 27.

TAO Ling, HUANG Peng, GU Ming,etal. Probability density distribution of wind pressure time series of low-rise buildings [J]. Journal of Tongji University: Natural Science, 2013, 41 (1): 27.

[7]Cao J X, Yoshida A, Saha P K,etal. Wind loading characteristics of solar arrays mounted on flat roofs [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 214.

[8]Stathopoulos T, Zisis I, Xypnitou E. Local and overall wind pressure and force coefficients for solar panels [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 125: 195.

[9]Japanese Industrial Standards Committee. JIS C 8955:2011 Design guide on structures for photovoltaic array[S]. Tokyo: Japanese Standards Association, 2011.

[10]Halder A, Mahadevan S. Probability, reliability and statistical methods in engineering design [M]. New York: John Wiley & Sons, 2000.

[11]McLaughlin M P. Regress+, appendix A: a compendium of common probability distributions, Version 2.3 [M]. Fairfax: McLean, 1999.

[12]Johnson N L, Kotz S, Balakrishnan N. Continuous univariate distributions (Vol.1)[M]. 2nd ed. New York: John Wiley & Sons, 1994.

[13]张相庭. 结构风工程: 理论·规范·实践 [M]. 北京: 中国建筑工业出版社, 2006.

ZHANG Xiangting. Structural wind engineering: theory, code and practice [M]. Beijing: China Architecture & Building Press, 2006.

Full-scale Measurement and Investigation of Wind Pressure Loadings on Typical Rooftop Photovoltaic Solar Panels

YU Xianglin1, DONG Rui2, 3, WANG Shouqiang3

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. College of Civil Engineering, Fuzhou University, Fuzhou 350108, China; 3. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract：A full-scale measurement of wind pressure loadings was conducted on photovoltaic (PV) solar panels mounted on the flat roof of a multipurpose low-rise building. According to the characteristics of wind pressure time series, several probability density functions were properly selected for nonlinear regression analysis of wind pressure coefficients of each gauging point. Numerical fittings of mean and peak (positive maxima and negative minima) and area-averaged peak pressure coefficients were performed and compared by using six probability distributions. The analysis results show that the probability distributions of negative minima and positive maxima of pressure coefficients are left-skewed and right-skewed, respectively. The mean pressure coefficient time series comply with unbiased distribution and the t distribution fits the measured data best, followed by Logistic, Normal, Type I EDV distribution, respectively; Type I EVD has the best fitting effect for peak values, and then the Lognormal distribution, Gamma distribution and Normal distribution in order; The most unfavorable pressure coefficient is dominated by negative peak pressure, that is, suction forces are predominant over wind forces on PV panels; The tributary area-averaged unfavorable pressure coefficient is recommended to take -2.3.

Key words：flat roof; Photovoltaic (PV) solar panel; full-scale experiment; pressure coefficient; extreme value distribution

文献标志码：A

中图分类号：TU312+.1; O211.3

基金项目：桥梁结构抗风技术交通行业重点实验室开放课题基金(KLWRTBMC14-03) ; 福建省自然科学基金(2015J05098)

收稿日期：2015—05—21

第一作者： 余香林(1984—)，男，博士生,主要研究方向为结构抗风和稳定. E-mail: 6yux@tongji.edu.cn