基于相似理论的锂电池三维电化学跨尺度建模

张立军， 程洪正

(1.同济大学 汽车学院,上海 201804; 2.同济大学 智能型新能源汽车协同创新中心,上海 201804)



基于相似理论的锂电池三维电化学跨尺度建模

张立军1,2， 程洪正1,2

(1.同济大学 汽车学院,上海 201804; 2.同济大学 智能型新能源汽车协同创新中心,上海 201804)

摘要：从抛物线型偏微分方程基本形式出发，利用量纲为一分析法推导了抛物线型偏微分方程的相似准则，并推广得到电化学过程的相似准则，从而确定原型与模型之间的电化学过程参数相似关系.利用Comsol Multiphysics软件进行了锂离子电池单元电化学过程的有限元建模与计算，验证了所建立相似准则和相似关系的正确性.模型验证结果表明电化学有限元建模方法能实现锂离子电池三维电化学过程的一致模拟，同时，高倍率充放电工况下电池内部不均匀性加剧，导致传统的通用准二维模型预测结果具有较大误差.因此，在电池单体设计及系统集成与管理过程中，有必要对基于准二维模型的状态估计算法进行修正，以避免电池局部过充过放而导致安全隐患.

关键词：锂离子电池; 电化学; 相似理论

动力电池是电动汽车的最核心部件之一，其性能影响到电动汽车的综合性能. 近年来，锂离子电池因其优异的综合性能倍受关注[1]. 锂离子电池性能设计包括结构、电极及隔膜材料、电流密度、容量、电压等的合理设计，对于电池各项外特性如功率与能量特性、效率、安全性、可靠性和寿命等都具有重要影响[2-4].

通常利用锂离子电池电化学模型进行电池电极、隔膜材料选择、结构设计，建立电池内部电化学动力学与外特性(工作电压、容量、功率特性)间的关系，在电池设计与优化方面有着广泛应用[5-6].

国内外研究中所提出的锂离子电池电化学模型主要分为经验模型、原理性模型. 经验模型主要有等效电路、阻抗谱模型等，其参数依赖于试验数据拟合，参数没有直接的电化学意义，只能反映电池外特性且预测精度有限[7]. 原理性模型分为单粒子模型(single particle model)[8-9]和通用准二维模型(Pseudo-2D)[10-12]. 单粒子模型由Haran等人[8]提出，单粒子模型忽略液相锂离子浓度和电势分布，仅在小于1C的低放电倍率时模型预测精度尚可[13]. 准二维模型由Newman， Fuller, Doyle等人[10-11]基于多孔电极理论和浓溶液理论建立. 随后建立起锂离子电池准三维[14]电化学模型，或考虑电化学—热耦合模型[15-17]. 国内外学者所建立的模型一般将电池单元简化为一维结构[10-12]，只考虑液相浓度、SOC、电流密度、生热速率等沿厚度方向分布；大多未充分考虑液相浓度、局部SOC(state of charge)、电流密度、电势、生热速率等沿极片面内分布的不均匀性. 锂离子电池内部的电流密度、局部浓度、SOC、电势等的极片面内方向分布并不均匀.在电动车用工况条件下，不均匀性加剧，导致采用以上简化模型与实际分布将具有较大偏差[15-17]. 因此，有必要建立严格的三维电化学模型，考虑极片面内电化学状态的不均匀性，提高电池内部电化学状态的预测精度.

电动车用锂离子电池单体一般包含上百个图1所示电池单元，每个电池单元又包括正极集流体、正极、隔膜、负极、负极集流体五层堆叠结构.由图1可知，单元各层结构的长度和宽度方向尺寸为分米级，而厚度方向尺寸为微米级，具有显著的跨尺度特征. 若直接按照电池单元的实际叠层结构尺寸进行电池内部电化学过程有限元建模与计算，将导致模型单元数量多、计算量大、难以实现的严重困难. 因此，如何解决跨尺度建模问题成为利用有限元方法进行电池内部电化学过程的预测的关键. 本文提出了应用于动力锂离子电池三维电化学过程跨尺度模拟方法并进行了验证分析.

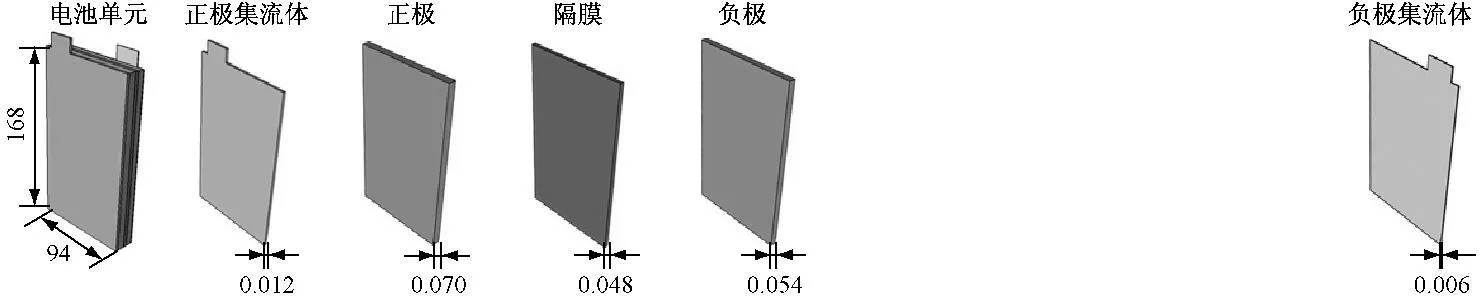
图1锂离子单电池结构示意图与三维尺寸(单位:mm)

Fig.1Schematic of lithium-ion battery cell(Unit: mm)

相似理论方法是人们在探索自然规律的过程中形成的一种模化方法，对流体力学、传热学等学科的发展曾发挥了不可估量的作用[18]. 在前期研究中，曾将相似理论应用于锂离子电池的温度场[19]、电场[20]及热应力场[21]的建模分析，有效地解决锂离子电池跨尺度有限元建模问题.

本文从抛物线型偏微分方程基本形式出发，利用量纲为一分析法推导了抛物线型偏微分方程的相似准则，并推广得到电化学过程控制方程的相似准则. 利用Comsol Multiphysics有限元软件进行了相似准则和相似关系正确性的验证，模型验证结果表明基于相似原理的电化学有限元建模方法能实现锂离子电池三维电化学过程的一致模拟，从而为锂离子电池的电性能设计、电化学状态估计与管理奠定良好的基础.

1锂离子电池电化学过程基本方程

1.1研究对象

图2所示为磷酸铁锂(LiFePO4)动力电池单元内部过程示意图.正极活性材料为磷酸铁锂(LiFePO4)，负极活性材料为石墨(C6)，正、负极集流体材料分别为铝和铜，电解液为1 mol·L-1的LiPF6溶液(1∶2 EC/DMC 溶剂).

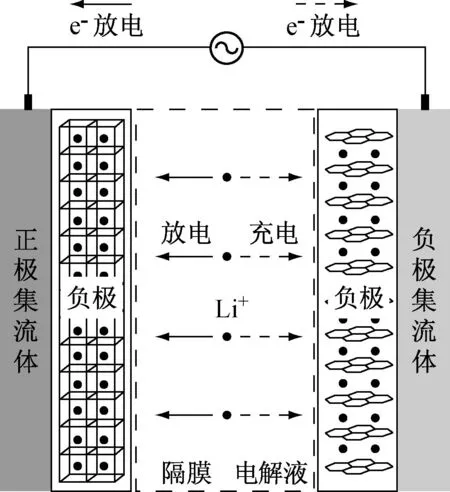
图2　锂离子电池内部过程示意图

电化学反应发生在多孔电极固、液相界面上，反应方程式如式(1)和式(2)所示.

正极反应

(1)

负极反应

(2)

式中,x为充放电过程中脱出或嵌入正数Li的质量分数.

1.2电化学过程控制方程

基于多孔电极理论、浓溶液理论、欧姆定律及电极反应动力学、物质与电荷能量守恒理论建立锂离子电池电化学过程模型.建模过程中对锂离子电池电化学过程进行了合理地简化假设：①假设电极活性材料由均匀球形颗粒构成；②电极层中只有固、液两相进行反应，无副反应发生; ③电化学反应符合Bulter-Volmer方程；④通过扩散和迁移在电解液里传输,忽略对流作用；⑤充放电过程体积膨胀忽略不计，孔隙率为恒定数值；⑥活性物质固体相扩散系数、离子迁移数与浓度、温度无关，为恒定数值.

1.2.1电荷守恒方程

在多孔活性电极保持电中性条件下，由电流的连续性可得以下方程

(3)

由欧姆定律，并考虑液相迁移过程有

(4)

(5)

固相电荷守恒方程如下:

(6)

液相电荷守恒方程如下：

(7)

假定锂离子电池以恒定电流放电，边界条件定义：

在负极极耳上

(8-1)

在正极极耳上

(8-2)

在集流体/电极活性材料界面

(8-3)

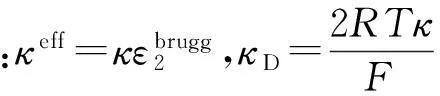
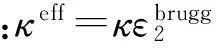
1.2.2质量守恒方程

(1)固相锂离子守恒方程

假定固相活性粒子为球状，固相锂离子嵌入和脱出电极活性粒子的扩散过程服从菲克(Fick)第二定律，以球坐标形式表达如下:

(9)

固相扩散过程的边界条件为

(10)

式中:c1为固相锂离子浓度;D1为固相扩散系数;r为活性颗粒径向坐标;Rs为颗粒半径.

(2)液相锂离子守恒方程

假定锂离子在电解液中的传输过程遵循浓溶液理论.考虑锂离子的扩散、电迁移过程以及界面反应产生/消耗，则液相锂离子守恒方程如下：

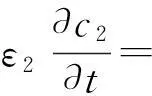
(11)

液相传质过程的边界条件为：正极与正极集流体界面、负极与负极集流体界面Ω上

(12)

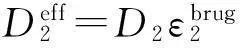
1.2.3电极反应动力学方程

活性电极粒子表面电化学反应过程由Butler-Volmer方程描述如下:

(13)

j0为交换电流密度

(14)

η为超电势:

(15)

式中:αa,αc为阳极、阴极的传递系数;K0为反应速率常数，仅与温度有关;Ue为平衡电势;RSEI为SEI膜电阻;c1,max为最大固相浓度;c1,surf为电极活性颗粒表面锂浓度.

2控制方程相似准则的推导

2.1抛物线型偏微分方程

三维传热、传质、电流传导过程方程均具有抛物线型偏微分方程的特征，如表1所示. 因此，传热、传质、电流传导过程的相似准则亦具有相似性，并均可由抛物线型方程的相似准则推广得到. 将抛物线型偏微分方程进行量纲为一处理，推导其相似准则.

表1　不同过程的控制方程相似性

三维抛物线型偏微分方程形式如下[22]：

(16)

通常结合初始条件及边界条件以确定偏微分方程解的唯一性.初始条件如下:

(17)

三类边界条件与边界定义为：

Dirichlet边界，(第一类)给定边界上待求变量的分布

(18)

Newman边界，(第二类)给出了在边界处待求变量的导数或偏导数

(19)

Robin边界条件，(第三类)定义待求变量与梯度值之间的函数关系

(20)

三类边界条件可统一写成如下:

(21)

式中，Γ是边界.

2.2抛物线型控制方程的相似准则

对式(16)～式(21)进行量纲为一处理，得到量纲为一控制方程如下：

(22)

量纲为一初始条件

(23)

量纲为一边界

(24)

其中，各纲量为一的表达式及含义如下：

量纲为一位置坐标

(25)

量纲为一源项

(26)

量纲为一吸收项系数

(27)

量纲为一时间，表征非稳态热传导进行的程度

(28)

量纲为一边界约束

(29)

量纲为一边界换热系数，表征非稳态导热条件下，物体内温度场的分布规律

(30)

量纲为一待求解量

(31)

由式(22)～式(24)可知量纲为一场量U为量纲为一的量{X,Y,Z,A,F,τ,B,W}的函数，亦即为抛物线型方程的相似准则数，如式(25)～式(31)所示.相似准则数{X，Y，Z，A，F，τ,B,W}既可作为模型相似的判定准则，又可基于相似准则数构造相似模型.

为解决电池物理场有限元建模的跨尺度难题，建立Z方向(厚度方向)尺寸扩大N倍的相似模型进行等效模拟. 由相似准则数{X,Y,Z,A,F,τ,B,W}相等的原则，可导出原型和相似模型的参数相似设置关系，如表2所示.

2.3抛物线型控制方程相似准则的推广

由于电化学过程的物理方程具有抛物线型方程的形式，可将抛物线型方程的相似准则推广映射到锂离子电池电化学过程控制方程中，得到电化学过程的原型与模型参数设置.

由式(9)可知，球形活性粒子域的固相扩散过程是一维过程，活性粒子半径不变的情形下，固相浓度分布及演变规律仅与粒子表面边界通量、固相扩散系数相关. 因此，只需原型与模型固相区域的表面局部电流密度、固相扩散系数满足以下关系，其中，以下标p表示原型，以下标m表示模型.

(32)

(33)

固相浓度即可满足分布

表2　抛物线型方程参数相似关系设置(原型：相似模型)

(34)

由于固相电荷守恒(6)、液相电荷守恒(7)、液相传质过程(11)的控制方程均为抛物线型偏微分方程，故各过程的原型与相似模型间参数相似关系可以参照抛物线型方程的参数相似关系设置表2直接导出，具体如表3所示.

当满足表3条件时，模型与原型的电化学过程相似，即

量纲为一固相浓度

(34)

量纲为一液相浓度

(35)

量纲为一固相电势

(36)

量纲为一液相电势

(37)

即待求解物理量的实际分布满足关系如下：

(38)

3基于有限元的相似准则验证

为验证表2、表3以及式(35)～式(38)所示相似准则和参数相似关系的正确性，基于Comsol Multiphysics有限元软件平台建立电池电化学过程的原型和相似模型，并对比了基于相似原理的三维电化学模型与准二维通用电化学模型在预测结果上的差异.

3.1有限元模型设置

锂离子电池电化学模型基本简化假设如1.2节所述，模型参数根据相似准则和电池工况条件设定，具体参数如表4所示.模型工况根据电池试验确定，选定为常温25 ℃下恒流1C放电至截止电压2.5 V.

表3　电化学过程原型与模型参数相似关系设置(原型：相似模型)

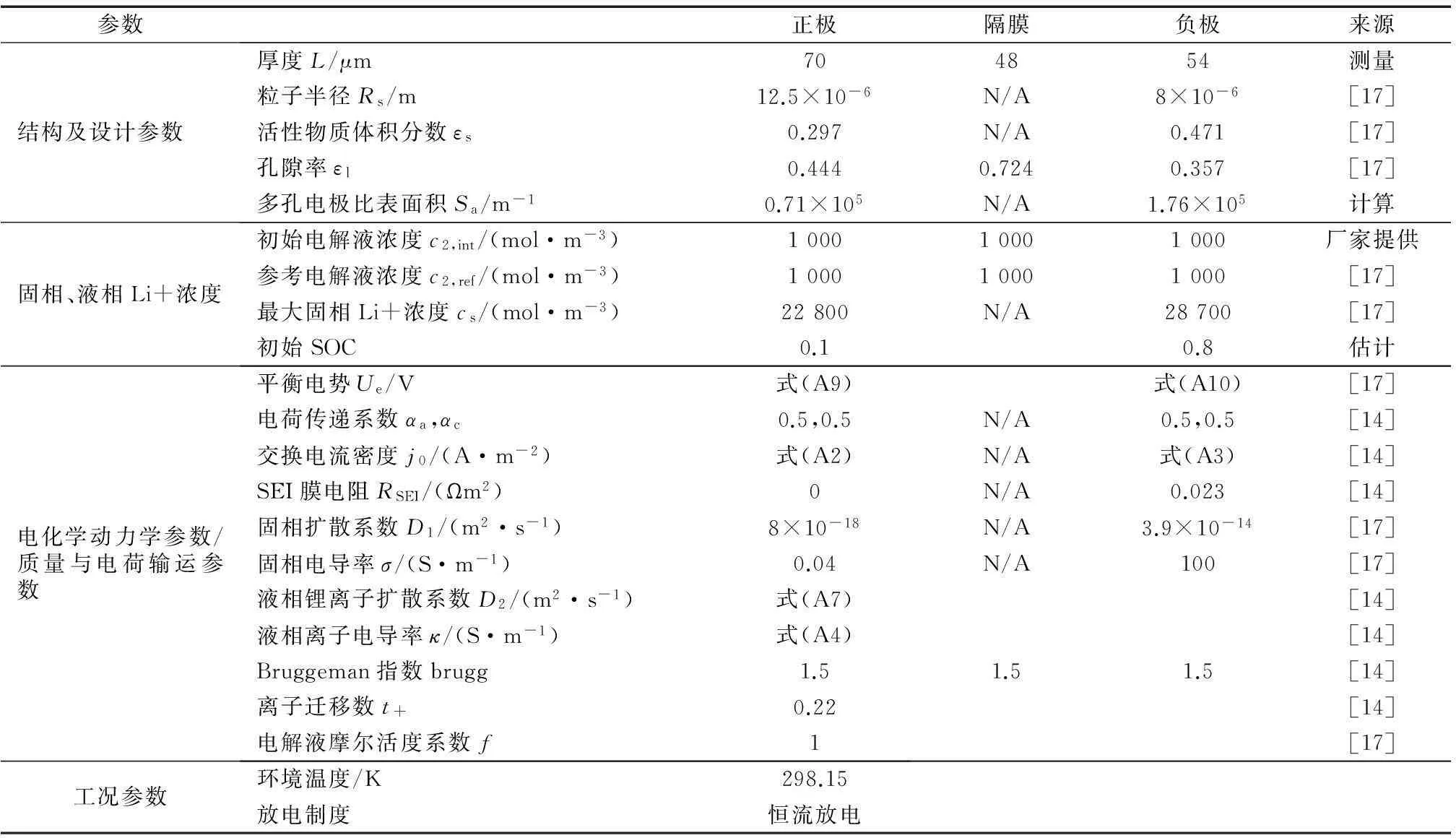
表4　电化学特性参数

在原型和相似模型的基本结构选择方面，由于叠层结构各层厚度尺寸为微米级别，与长度和宽度方向尺寸相差达到3个数量级.为保证有限元模型单元长宽比在合适的范围内，分别将厚度方向放大1 000倍和放大2 000倍得到的模型作为原型和相似模型，如图3所示.其中，原型的单元总数为15 408，相似模型的单元总数为30 816.利用Comsol Multiphisics软件分别对原型和相似模型，进行相似准则和相似关系的验证计算.

a原型b相似模型

图3电化学过程原型和相似模型

Fig.3Prototype and model of electro-chemical process

正负极平衡电势Ue表达式分别如式(39)和式(40)所示[17]

Ue,pos=2.567 5+57.69[1-tan(100θ+2.916 4)]+0.442 953arctan(-65.419 28θ+64.897 41)+0.097 237arctan(-160.905 8θ+154.590)

(39)

Ue,neg=0.637 9+0.541 6exp(-305.530 9θ)+

(40)

3.2相似准则有限元验证结果分析

选取了电化学过程液相浓度场、固相浓度场、液相电势场的空间分布和对应测点的时间历程作为原型和相似模型相似关系的评价指标，对应测点的坐标如表5所示.

表5　测点坐标

图4～图7所示为原型和模型计算结果.图4a、图4b分别为原型放电结束时刻液相浓度空间表面和内部分布图，图4c和图4d分别为模型放电结束时刻液相浓度空间分布图，图5a和图5b分别为原型放电结束时刻固相浓度空间表面和内部分布图，图5c和图5d为模型放电结束时刻固相浓度空间表面和内部分布图.图6a和图6b分别为原型和模型放电结束时刻液相电势空间分布图.图7a和图7b分别为原型和模型对应测点液相浓度和固相浓度的时间历程曲线.

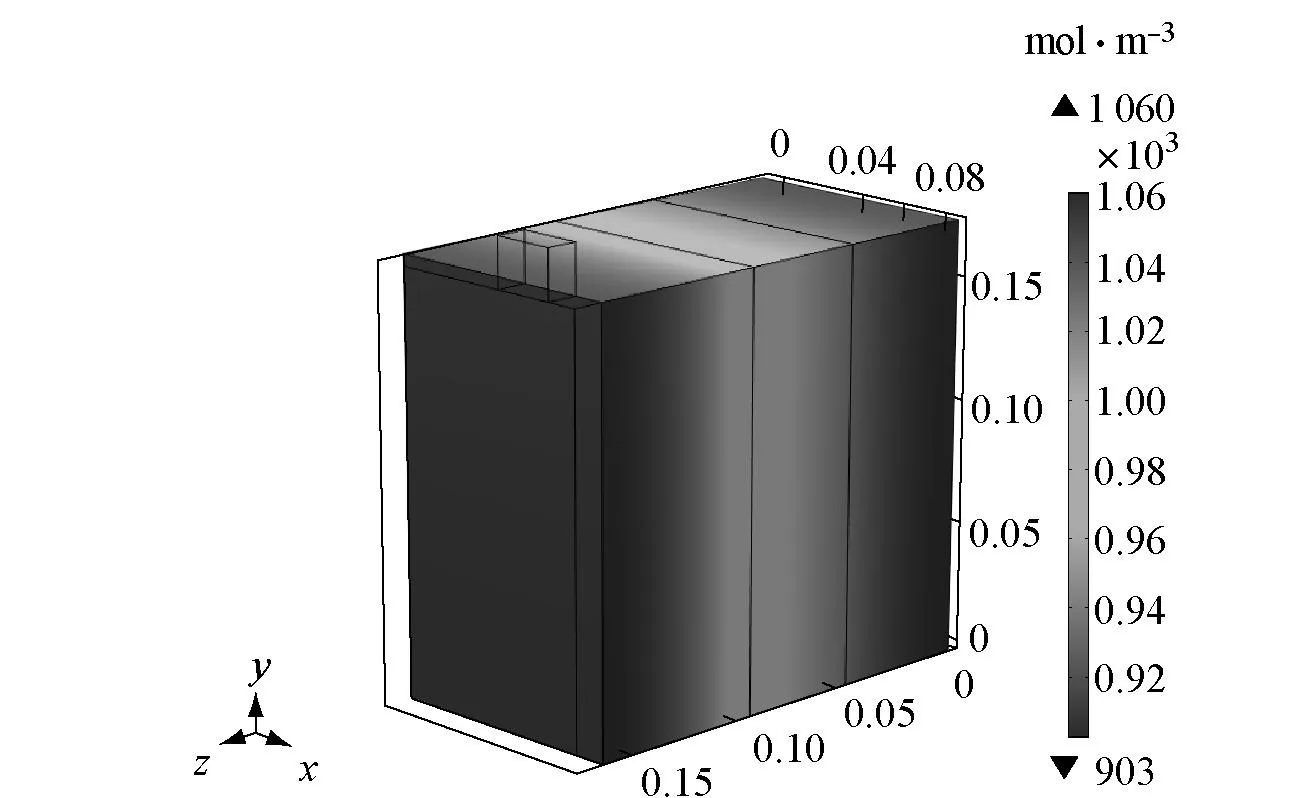
a 放电结束时刻原型液相浓度表面分布

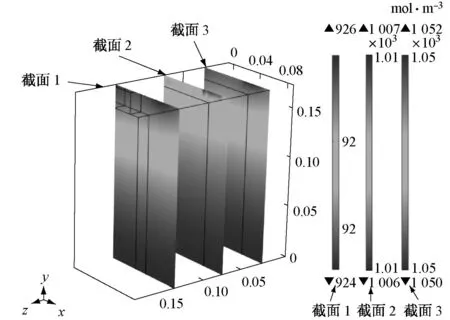
b 放电结束时刻原型液相浓度内部分布

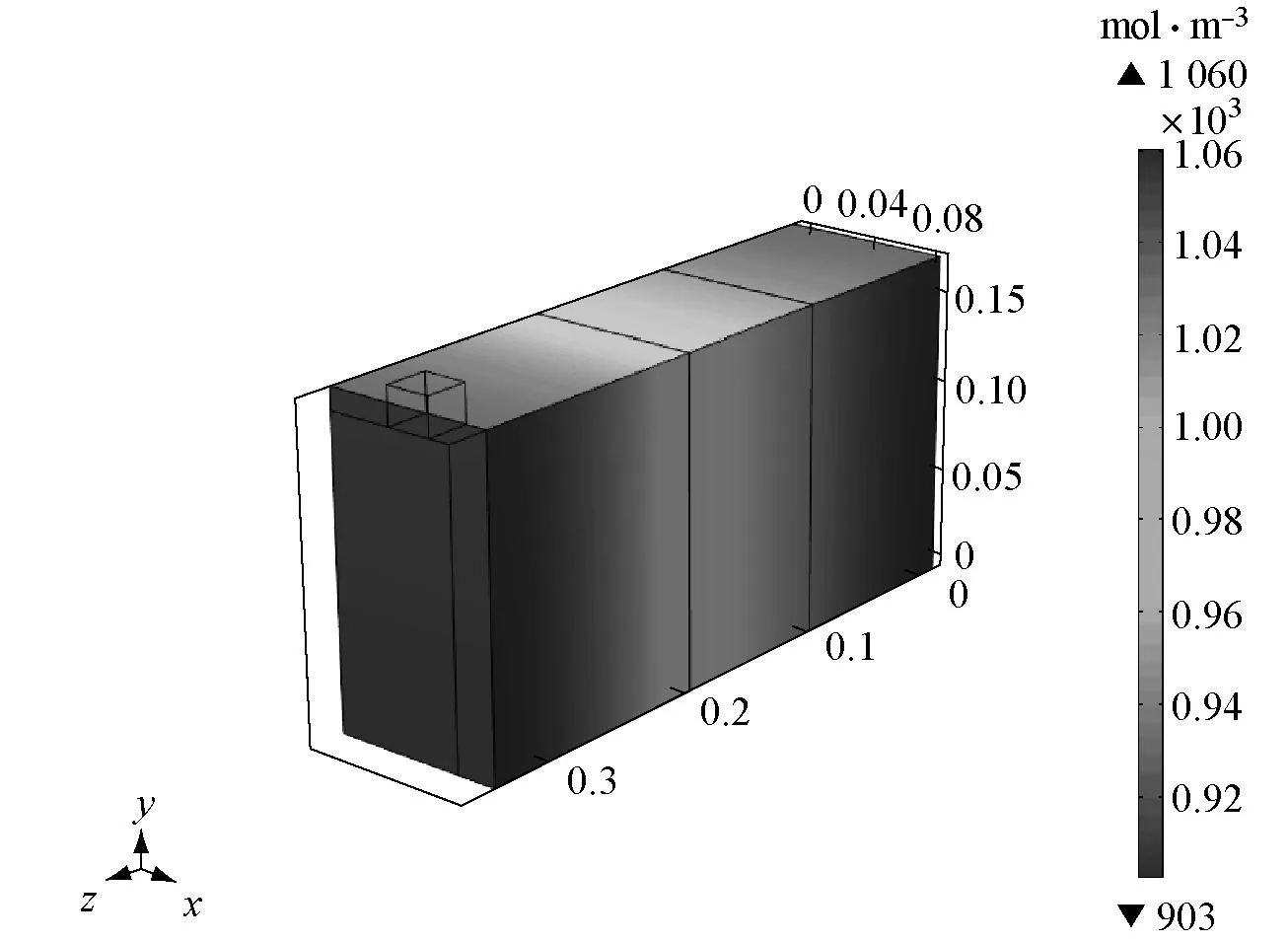
c 放电结束时刻模型液相浓度表面分布

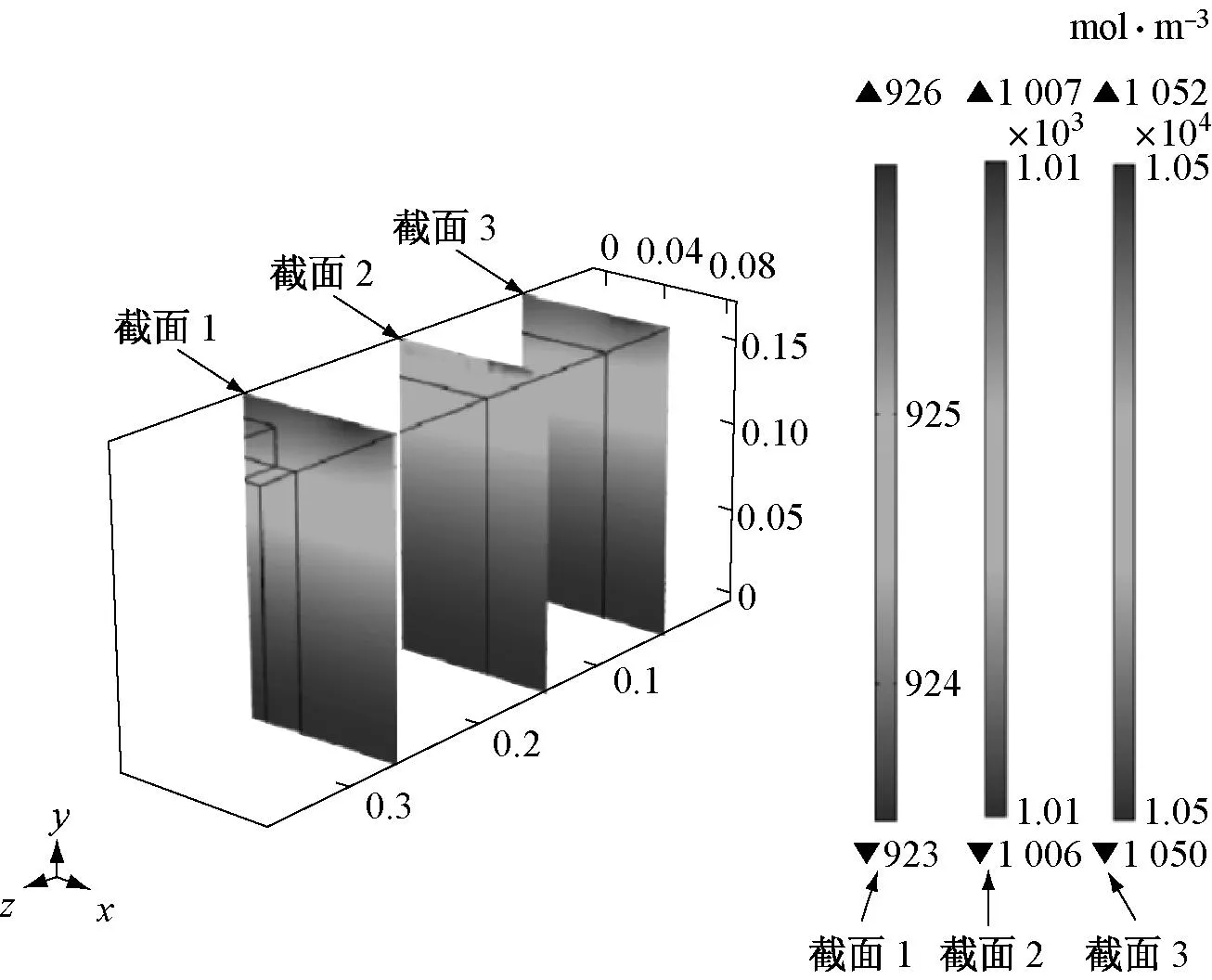
d 放电结束时刻模型液相浓度内部分布

Fig.4Comparison of electrolyte concentration between prototype and scale model in 1C discharge period

由仿真结果可知，在恒流放电过程中，负极区域电解液较正极区域浓度高，因而锂离子从负极区域向正极区域扩散和迁移，如图4所示.固相中负极区域锂离子脱出活性粒子，正极区域锂锂离子嵌入电极活性粒子，导致正极固相浓度升高，负极固相浓度降低，如图7b所示.

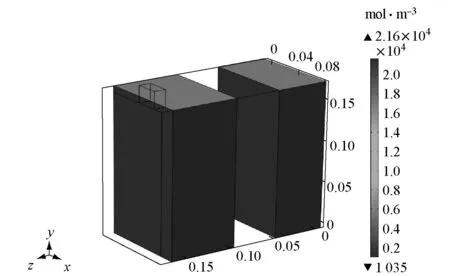
a 放电结束时刻原型液相固度表面分布

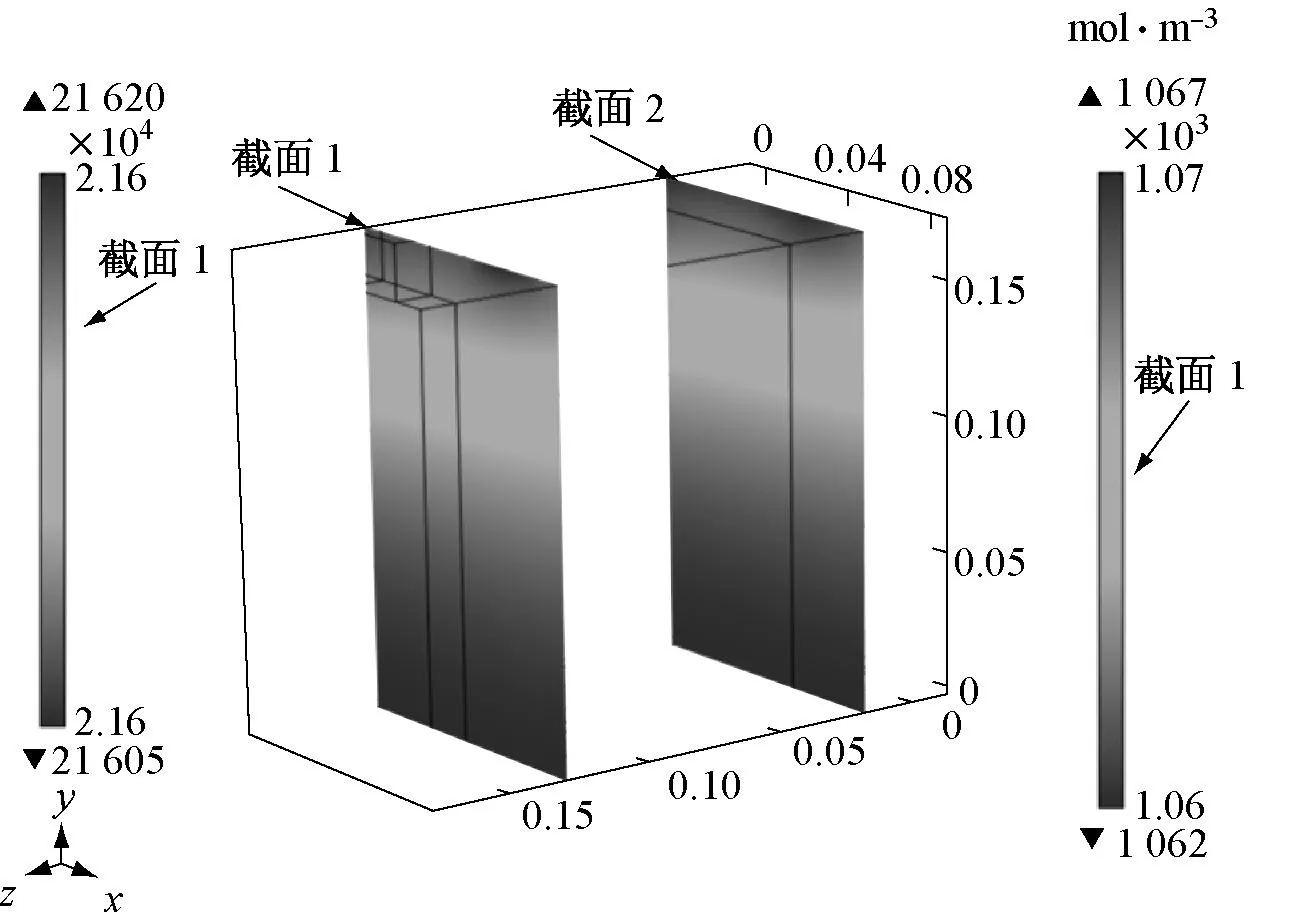
b 结束时刻原型固相浓度内部分布

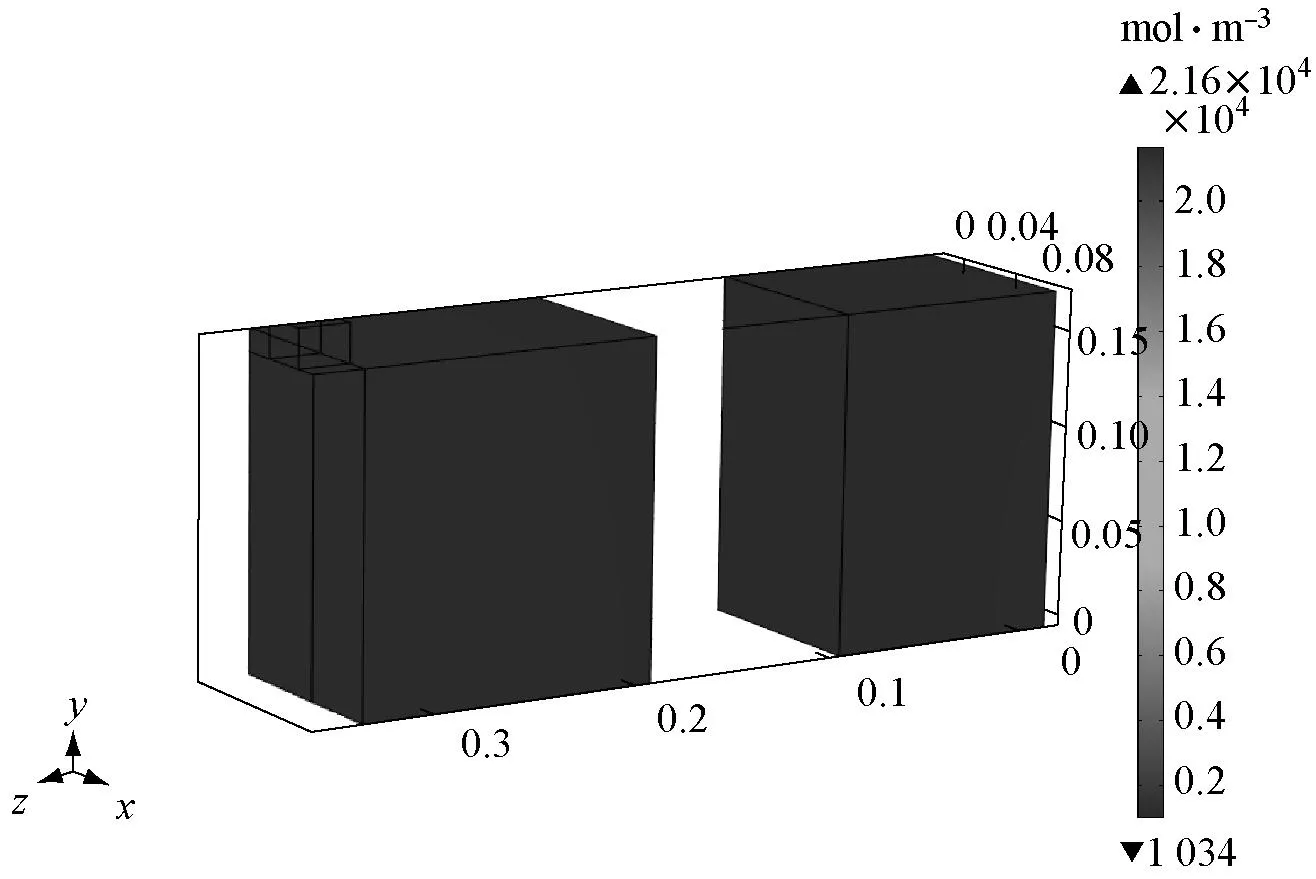
c 结束时刻模型固相浓度表面分布

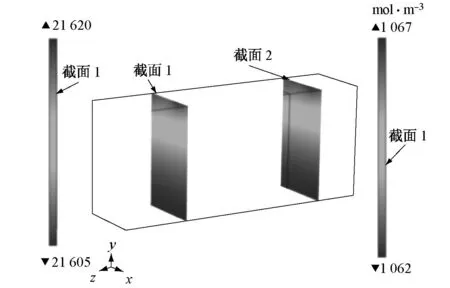
d 放电结束时刻模型固相浓度内部分布

Fig.5Comparison of solid phase concentration between prototype and scale model in 1C discharge

由图4～图7计算结果可知，在忽略有限元计算的误差情况下，相似模型与原型的电化学过程完全相似.即电化学过程液相浓度场、固相浓度场、液相电势场的空间分布(最大值、最小值和分布规律)和时间历程的完全一致，并与理论推导结果式(35)～式(38)相符.

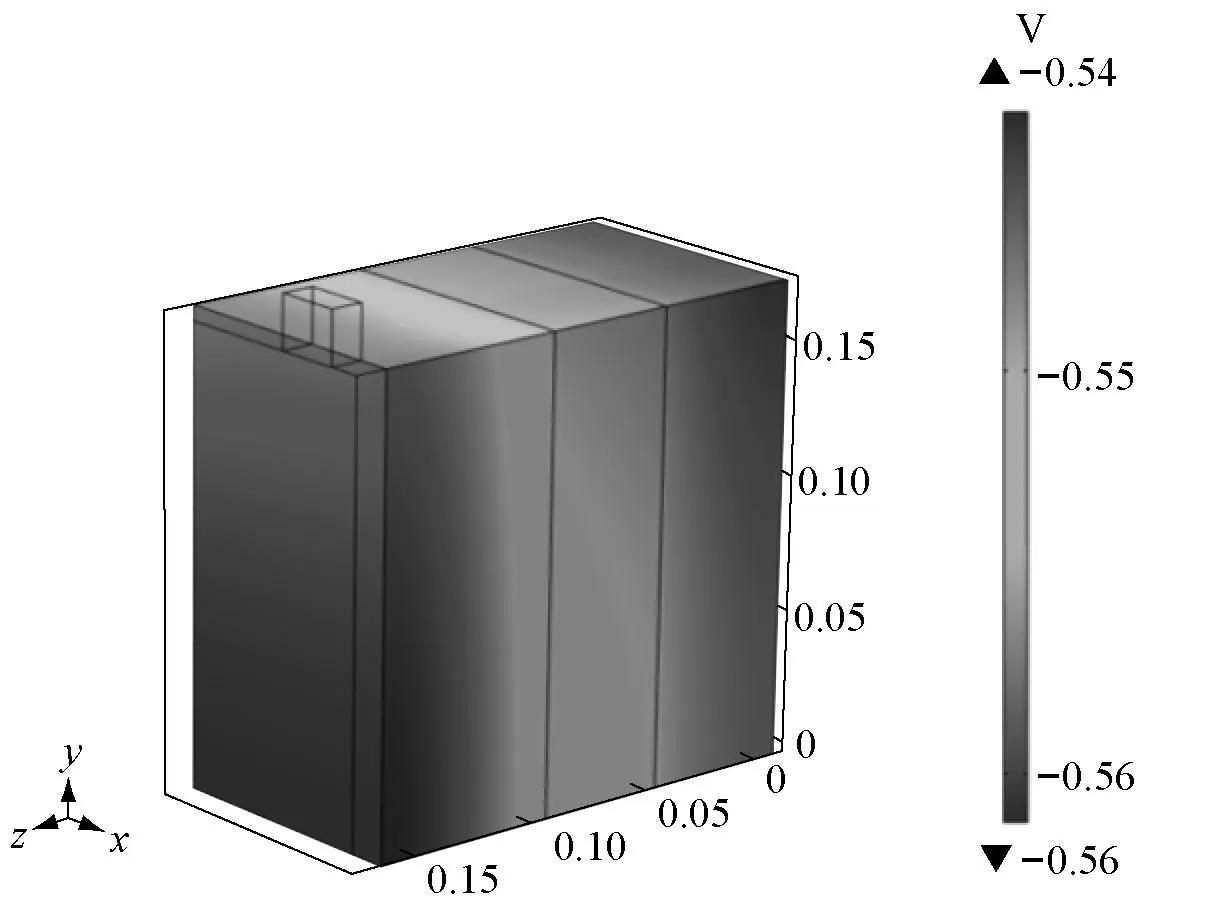
a 放电结束时刻原型液相电势表面分布

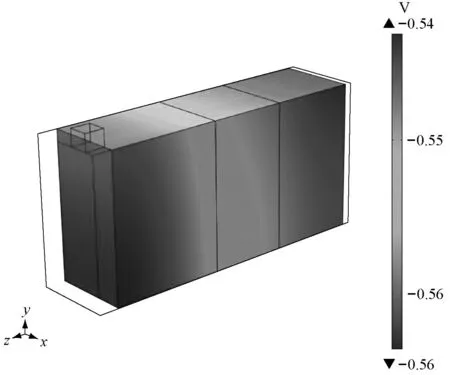
b 放电结束时刻原型液相浓度表面分布

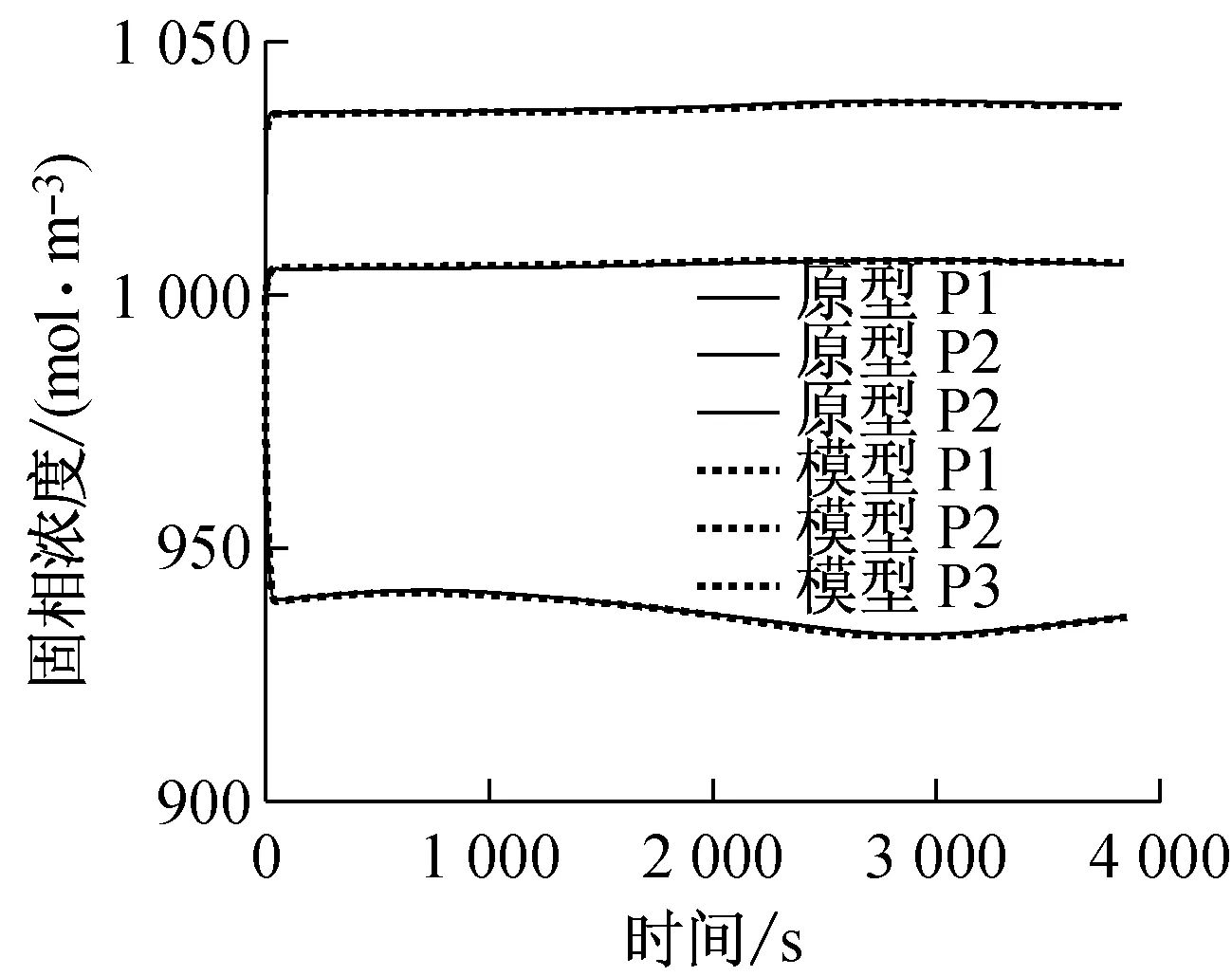
a 原型和模型对应测点液相浓度时间历程对比

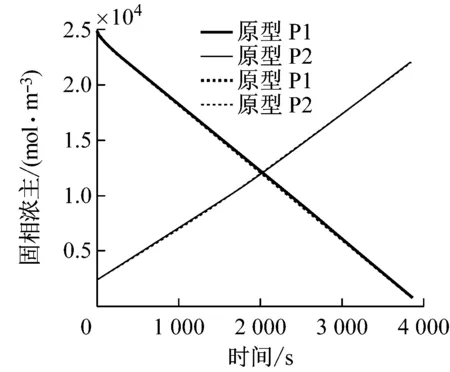
b 原型和模型对应测点固相浓度时间历程对比

Fig.7Comparison of time history at corresponding points between prototype and scale model

因此，理论推导确定的相似准则和相似关系是成立的，进一步地，模型验证结果表明电化学有限元建模方法能实现锂离子电池三维电化学过程跨尺度建模的一致模拟.

3.3计算效率的讨论

分别采用原始模型、厚度放大100倍模型与200倍的相似模型进行仿真，对比其计算精度与效率，计算硬件平台为24核CPU 64G内存的工作站，计算效率如表6所示.

表6　不同模型计算效率对比

对比结果显示，厚度放大100倍模型与200倍的相似模型相对于原始结构在计算效率上有显著优势.

3.4通用准二维(Pseudo-2D)模型与基于相似原理三维模型计算结果对比

目前，通用准二维(Pseudo-2D)模型[10-12]忽略内部浓度场、电势场展向(各层面内)状态的不均匀性，将导致准二维模型的仿真误差.为评价通用准二维(Pseudo-2D)模型与基于相似原理的三维模型仿真结果的差异，分别提取两种模型不同倍率(1/3C、1C、2C、4C)放电过程工作电压，如图8所示.

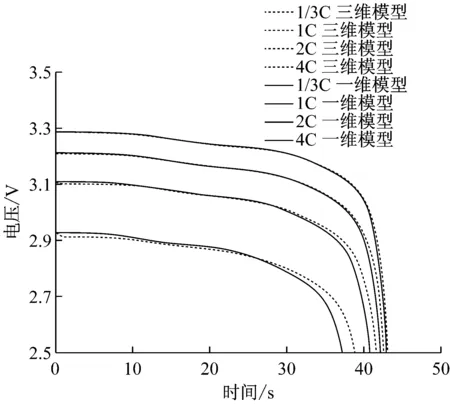
图8　准二维模型与三维模型不同倍率放电阶段电压对比

由图8可知，在不高于1C放电倍率的情况下，准二维模型与三维模型电池仿真结果差异很小. 随着放电倍率的升高，准二维模型与三维模型电池工作电压仿真结果差异加大.4C放电情况放电容量相对三维模型偏高2.6%，且准二维模型对电池放电容量的预测产生正偏差.

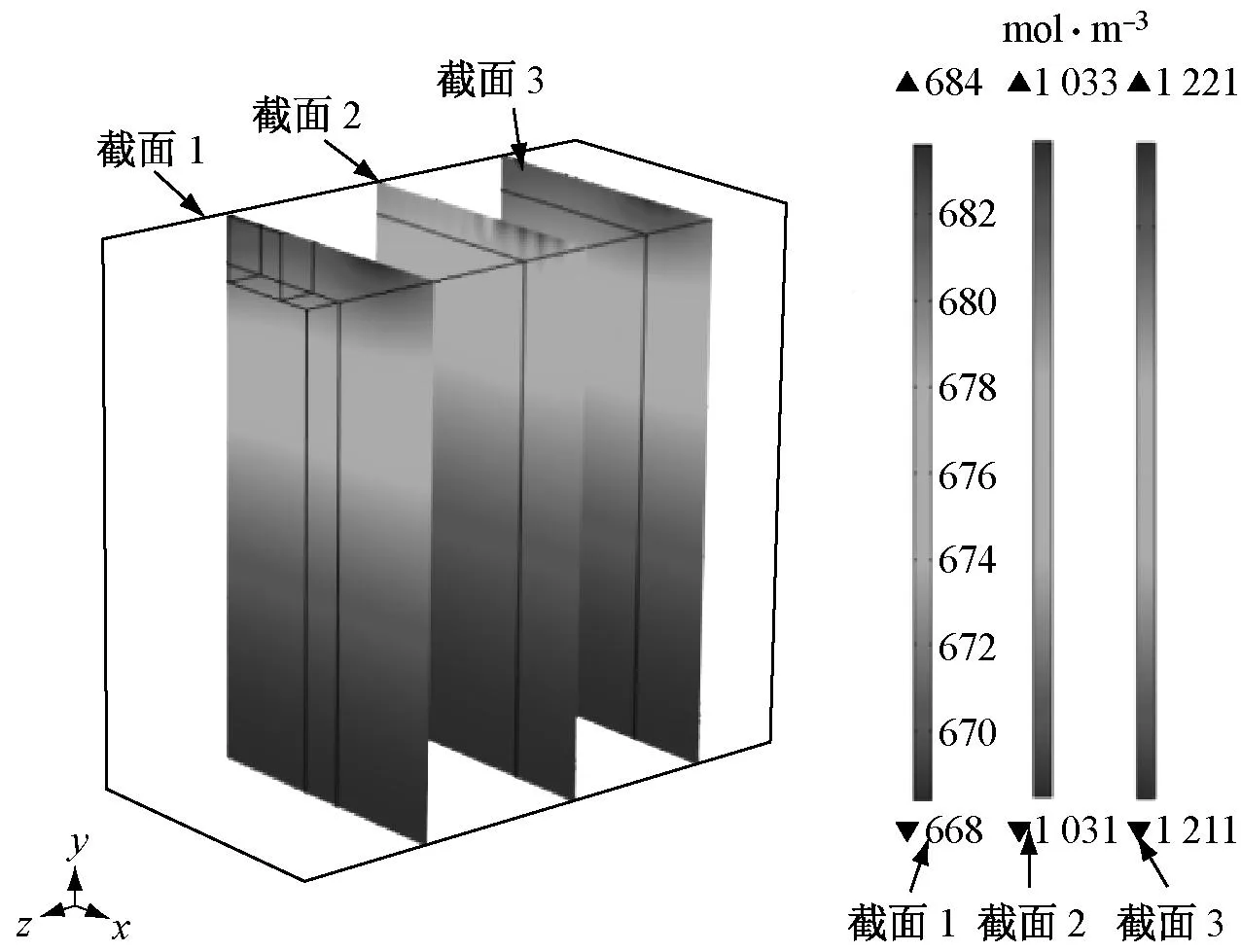
图9　三维模型4C放电结束时刻液相浓度分布

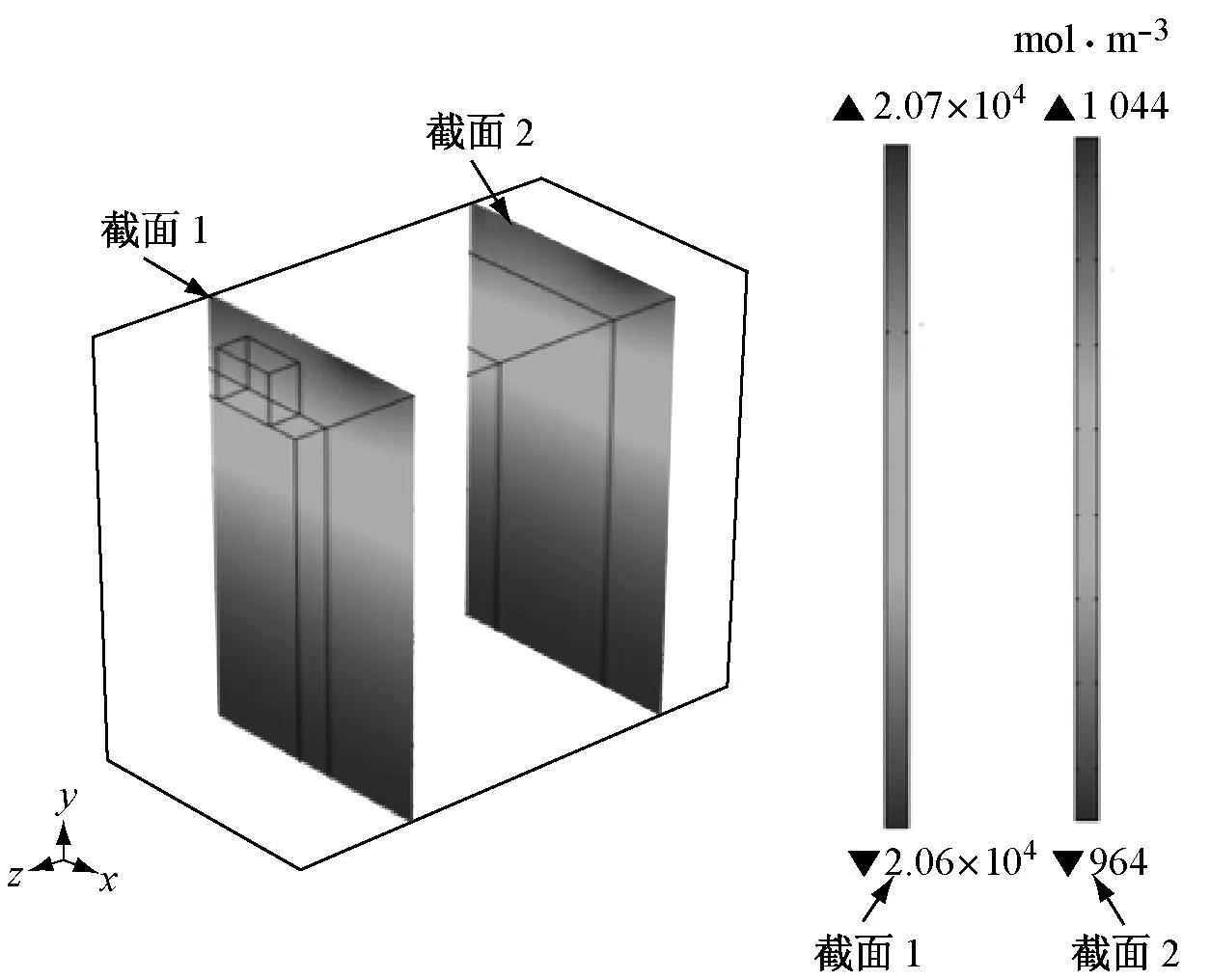
图10　4C放电结束时刻固相浓度分布

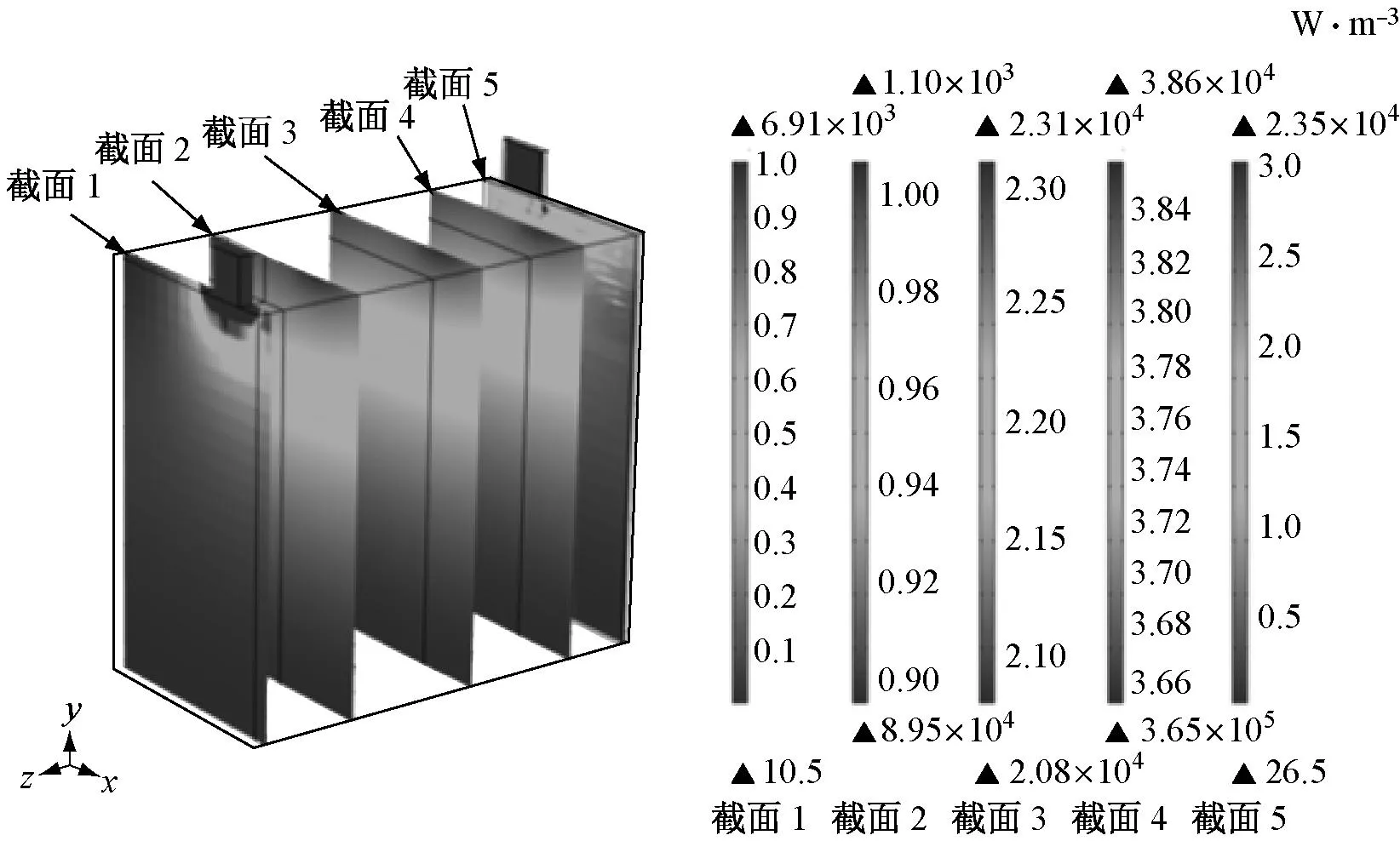
图11　4C放电结束时刻生热速率分布

准二维模型与三维模型工作电压的差异来源于电池内部浓度场、电势场等展向(面内)分布的不均匀性，如图9和图10所示,进而导致内部生热速率分布不均匀,如图11所示.

因此，在电池系统集成和管理过程中，有必要对基于准二维模型的状态估计算法进行修正；在电池单体结构设计则应合理设计极耳结构，减小内部状态的不均匀性，以避免电池运行过程出现局部过充过放等问题导致电池失效及安全问题的发生.

4结论

基于相似理论的锂离子电池跨尺度建模研究主要得到以下结论：

(1)从抛物线型偏微分方程基本形式出发，利用量纲为一分析法推导了抛物线型偏微分方程的相似准则，并推广得到电化学过程控制方程的相似准则，能够实现电化学过程时间历程和空间分布的一致模拟；

(2)在某一方向几何尺寸缩放N倍，为实现电化学过程完全相似，相应方向的液相扩散系数、固相电导率、液相电导率相应缩小或放大N2倍，而其他参数保持不变.

(3)利用相似原理有助于解决锂离子电池叠层结构跨尺度建模问题，并为锂离子电池多物理场跨尺度建模问题的解决提供思路.

(4)由于高倍率放电工况下电池内部不均匀性加剧，导致传统的通用准二维模型容量预测结果具有正误差.因此，在电池单体设计及系统集成与管理过程中，有必要对基于准二维模型的状态估计算法进行修正，以避免电池局部过充过放而导致安全隐患.

由于电化学过程与温度场存在相互耦合，在后续研究中将考虑这一耦合作用，建立电化学-热耦合模型进行电池内部温度场、电化学状态的精确预测.

参考文献:

[1]Salvadori A, Bosco E, Grazioli D. A computational homogenization approach for Li-ion battery cells: part 1—formulation[J]. Journal of the Mechanics and Physics of Solids, 2014, 65: 114.

[2]黄可龙，王兆翔，刘素琴. 锂离子电池原理与关键技术[M]. 北京: 化学工业出版社, 2011.

HUANG Kelong, WANG Zhaoxiang, LIU Suqin. The principle and key technology of lithium ion battery[M]. Beijing: Chemical Industry Press, 2011.

[3]李相哲，苏芳，林道勇. 电动汽车动力电源系统[M]. 北京: 化学工业出版社, 2011.

LI Xiangzhe, SU Fang, LIN Daoyong. Power supply system of electric vehicle [M]. Beijing: Chemical Industry Press, 2011.

[4]郭伟春，付艳恕，王丹，等. 车载锂离子电池放电性能影响因素研究[J]. 电源技术, 2013, 37(3): 372.

[5]Franco A A. Multiscale modelling and numerical simulation of rechargeable lithium ion batteries: concepts, methods and challenges[J]. RSC Advances, 2013, 3(32): 13027.

[6]Wu W, Xiao X, Huang X. The effect of battery design parameters on heat generation and utilization in a Li-ion cell[J].ElectrochimicaActa, 2012, 83: 227.

[7]Hu X, Li S, Peng H. A comparative study of equivalent circuit models for Li-ion batteries[J]. Journal of Power Sources, 2012, 198: 359.

[8]Han X, Ouyang M, Lu L,etal. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part I: Diffusion simplification and single particle model[J]. Journal of Power Sources, 2015,278:802.

[9]Guo M, Sikha G, White R E. Single-particle model for a lithium-ion cell: thermal behavior[J]. Journal of The Electrochemical Society, 2011, 158(2): 122.

[10]Fuller T F. Simulation and optimization of the dual lithium ion insertion cell[J]. Journal of The Electrochemical Society, 1994, 141(1): 1.

[11]Doyle M, Newman J, Gozdz A S,etal. Comparison of modeling predictions with experimental data from plastic lithium ion cells[J]. Journal of the Electrochemical Society, 1996, 143(6): 1890.

[12]Yan B, Lim C, Yin L,etal. Simulation of heat generation in a reconstructed LiCoO2 cathode during galvanostatic discharge[J].ElectrochimicaActa, 2013, 100: 171.

[13]Kumaresan K, Sikha G, White R E. Thermal model for a Li-ion cell[J]. Journal of the Electrochemical Society, 2008, 155(2): 164.

[14]Gerver R E, Meyers J P. Three-dimension modeling of electrochemical performance and heat generation of lithium-ion batteries in tabbed planar configurations[J]. Journal of The Electrochemical Society, 2011, 158(7): 835.

[15]Guo M, White R E. A distributed thermal model for a Li-ion electrode plate pair[J]. Journal of Power Sources, 2013, 221: 334.

[16]Smith K, Wang C. Power and thermal characterization of a lithium-ion battery pack for hybrid-electric vehicles[J]. Journal of Power Sources, 2006, 160(1): 662.

[17]Saw L H, Ye Y, Tay A A O. Electrochemical-thermal analysis of 18650 lithium ion phosphate cell[J]. Energy Conversion and Management. 2013, 75: 162.

[18]王丰. 相似理论及其在传热学中的应用[M]. 北京: 高等教育出版社, 1990.

Wang Feng. Similarity theory and its application to heat transfer theory[M]. Beijing: Higher Education Press, 1990.

[19]程洪正，张立军，阮丞，等. 锂离子电池温度场相似准则推导与有限元验证[J]. 同济大学学报:自然科学版, 2013，41(8): 1249.

Cheng H, Zhang L, Ruan C. Validation of similarity criterions of temperature field inside lithium-ion battery[J]. Journal of Tongji University: Natural Science, 2013, 41(8): 1249.

[20]张立军，程洪正，阮丞，等. 锂离子电池电场相似准则的推导与有限元验证[J]. 汽车工程, 2013，35(8): 691.

ZHANG Lijun, CHENG Hongzheng, RUAN Cheng,etal. Derivation and FEM validation of similarity criterions of electric field inside of lithium-ion battery[J]. Automotive Engineering, 2013, 35(8): 691.

[21]程洪正，张立军，阮丞，等. 锂离子电池应力应变场的相似准则推导与有限元验证[J]. 中国科学:技术科学, 2013,43(6): 670.

CHENG Hongzheng, ZHANG Lijun, RUAN Cheng,etal. Derivation and FEM validation of similarity criteria of thermal stress-strain field inside of lithium-ion battery[J].ScientiaSinicaTechnologica, 2013,43(6): 670.

[22]陈恕行. 现代偏微分方程导论[M]. 北京: 科学出版社,2005.

CHEN Shuxing. Introduction to modern partial differential equation[M]. Beijiing: Science Press, 2005.

Three-dimension Multi-scale Electro-chemical Model for Lithium-ion Battery Based on Similarity Theory

ZHANG Lijun1,2, CHENG Hongzheng1,2

(1. College of Automotive Studies, Tongji University, Shanghai 201804, China; 2. Synergy Innovation Center of Intelligent New-energy Vehicle， Tongji University, Shanghai 201804, China)

Abstract：A dimensional analysis method was performed to derive similarity criteria and the similarity coefficients of parabolic partial differential equation, and then it was further generalized to deduce the similarity coefficients of the electrochemical process. To validate the similarity criteria and the similarity coefficients, three-dimension finite element models of electrochemical process of lithium ion battery under specified conditions were established with the software of Comsol Multiphysics. The simulation results show that the similarity criteria and the similarity coefficients are certified to be correct and the modelling method based on the similarity theory can achieve equivalent simulation. Moreover, the simulation results reveal that the inner state of the battery tends to be uneven under high rate operation, thus corresponding measurements in design and management based on conventional Pseudo-2D model should be modified to avoid safety issues due to a local over-charge or over-discharge.

Key words：lithium ion battery; electro-chemical field; similarity theory

文献标志码：A

中图分类号：U463.51

通讯作者：程洪正(1989—)，男，博士生，主要研究方向为新能源汽车动力总成与关键部件开发.E-mail：chenghz2007@163.com

基金项目：国家“九七三”重点基础研究发展计划(2011CB711201)

收稿日期：2015—06—02

第一作者： 张立军(1972—)，男，教授，工学博士，博士生导师，主要研究方向为新能源汽车动力总成集成与控制、汽车振动与噪声的分析与控制.E-mail：tjedu_zhanglijun@tongji.edu.cn