基于布谷鸟算法的给水管网调压阀优化设计

陶　涛， 张　俊， 信昆仑， 李树平

(同济大学 环境科学与工程学院，上海 200092)



基于布谷鸟算法的给水管网调压阀优化设计

陶涛， 张俊， 信昆仑， 李树平

(同济大学 环境科学与工程学院，上海 200092)

摘要：针对城市给水管网漏损日益严重的问题，采用压力管理的策略，通过在管网中安装调压阀降低管网压力，从而达到减少管网真实漏损的目的.利用一个新的优化算法布谷鸟算法，建立管网调压阀优化模型，确定调压阀的数量、最优安装位置以及最优操作方式,并在算例管网中与遗传算法进行对比测试.结果显示:布谷鸟算法由于其调节参数少，随机搜索路径优，在调压阀优化设计中显示了更优秀的优化能力，显示了强大的算法应用可扩展性，使得对真实管网通过最优化算法来确定最佳阀门控制策略成为可能.

关键词：给水管网；布谷鸟算法；降低漏损；调压阀优化设计

目前，给水管网漏损控制已经成为全世界供水企业关心的重要课题.报告显示，在许多国家，漏损已经占供水总量的30%，甚至在有些城市高达40%[1].许多因素会导致管网中管道情况恶化，最终导致管网物理漏损增加.其中影响漏损一个非常重要的因素就是压力[2].在实际运行中，给水管网是根据最高日最高时用水量设计的，因此管网会在很长一段时间内承受过高的压力，尤其是深夜用水量较少的时候.

压力管理是国际水协(IWA)推行的用于控制水量损失的四种策略之一.在保证用户正常用水的同时降低压力，可以减少给水管网物理漏损.从历史上看，供水企业一直依赖于调压阀将管道下游压力保持在固定水平.但是当压力在低流量下略有增加时，这种方法就存在缺陷，尤其是在夜间.

Jowitt和Xu[3]建立给水管网压力变化下漏损模型，利用线性理论求解含有阀门开度变量的管网方程来确定管网中最佳阀门位置以及不同工况下调压阀开启度，优化压力分布达到降低漏损的目的.

Nicolini[4]以阀门数量最少和漏损量最小为目标，建立了漏损控制的多目标优化模型，通过基于分解的多目标遗传算法求解，同时优化调压阀的数量和安装位置，为漏损控制提出了新的策略和方法.

Ali和Mohammed E[5]首先对给水管网管道预处理，将管道按优先等级排序去除不可能安装阀门的管道，然后利用虚拟阀门改变海森威廉方程中参数，找到该参数与阀门开启度之间的关系，利用遗传算法GA同时优化阀门位置与开启度.有效地减少了搜索空间，提升了计算效率.即使如此，在处理下文所提到的算例时，依然需要在初始种群为100的情况下，使用遗传算法，运行大概160代才能得到最优结果.

本文利用新型的智能优化算法布谷鸟算法，建立管网调压阀优化模型，该模型是一个双层优化模型.首先在第一层优化模型中确定减压阀的数量、最优安装位置，然后根据上层的结果在第二层优化模型中确定阀门最优操作方式.

1布谷鸟算法

布谷鸟算法(Cuckoo Search，简称CS)是由YANG Xinshe和Suash Deb[6]模拟布谷鸟选巢产卵的自然生物行为提出的一种具有全局收敛性的新型智能优化算法.该算法主要是基于寄生巢更新机理与莱维飞行(Levy flight)搜索原理两个方面，其主要优点是参数少、操作简单、随机搜索路径优和寻优能力强等.目前对布谷鸟算法的研究还处于起步阶段，还没有发现有文献将布谷鸟算法应用到给水管网调压阀优化设计问题中.

1.1布谷鸟算法假设

为模拟布谷鸟选巢产卵这一生物行为，需要以下三个假设：①布谷鸟一次只产一个卵，并随机选择寄生巢穴孵化它.巢穴中的一个卵代表这组解决方案中的一个目标未知量的解.在单目标优化设计中，每个巢穴只有一个卵表示一个单目标解决方案；②在随机选择的一组寄生巢中，最好的寄生巢将被保留到下一代；③可利用的寄生巢数量是固定的，一个寄生巢的主人能发现一个外来鸟蛋的概率为P(即生成新的解决方案的概率为P).

1.2布谷鸟算法流程

布谷鸟算法是具有“生成+检测”(generate-and-test)的迭代过程的搜索算法，包括5个基本要素：参数编码，初始群体设定，适应度函数设计，优化设计操作及算法控制参数的选择(发现概率P和步长控制α等).

标准布谷鸟算法的求解流程为①分析实际问题，确定参数集编码方式；②初始化种群，生成初始群体；③对种群中每个巢穴进行评价，计算适应度值；④进行终止条件判断，若满足则跳到第7步，否则进入下一步；⑤采用莱维飞行生成新巢穴，并且计算适应度值.如果新巢穴优于旧巢穴，则用新巢穴替换旧巢穴;⑥按发现概率P丢弃巢穴,用偏好随机游动产生新巢穴替代丢弃的巢穴,同时保留最优的巢穴，跳到第3步进行继续计算；⑦输出种群中具有最优适应度值的巢穴作为问题的满意解或最优解.布谷鸟算法的具体步骤如图1所示.

1.3布谷鸟算法两个更新步骤

在图1所示的布谷鸟算法流程图中，存在两个巢穴优化更新方式，下面给出基本布谷鸟算法的两个核心更新步骤.

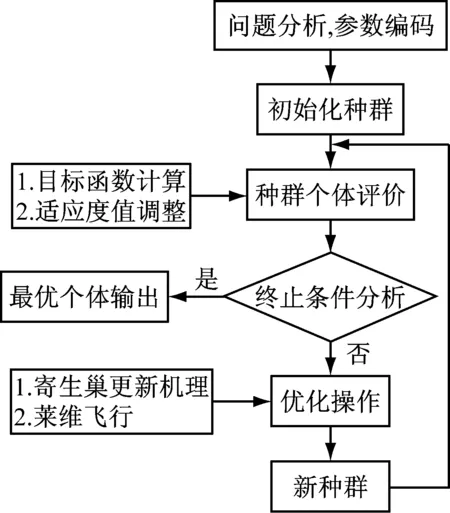
图1　布谷鸟算法流程图

1.3.1基于莱维飞行特征的位置更新

第一个更新方式主要利用式(1)对巢穴的位置进行更新操作

(1)

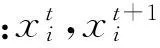
步长随机搜索路径L(β)计算如下:

(2)

式中：μ,ν为通过标准正态分布随机产生的实数；x0为目前最佳巢穴位置；σ为通过式(3)随机产生的实数.

(3)

式中：β为一常数，取值范围为1≤β≤3;Γ表示伽马分布.

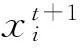
1.3.2基于寄生巢更新机理的位置更新

第二个更新方式是模拟布谷鸟的卵被巢穴原主人发现后，它会抛弃旧巢穴生成新的巢穴的思想和机制.

更新步骤如下: 首先随机生成一个服从[0,1]均匀分布的随机数r，然后将r与发现概率P比较，若r

(4)

2调压阀优化模型

在第一层确定阀门位置时，根据管道的流量分配，将管道的局部损失系数改为一个确定的值，表示该条管道上有一个虚拟阀门.因此管网每增加一条管道，搜索空间仅仅只增加1，极大地提高了计算效率，能快速确定阀门的最佳位置.在第二层优化时利用第一层的结果确定不同时段的阀门开启度.

2.1第一层优化模型

根据Araujo[7]的研究，阀门的位置对管网物理漏损的影响远远大于阀门数量.考虑到工程师能够结合项目经费与工程要求来确定阀门数量，故将阀门数量当作已知条件，在本层优化模型中只确定最佳阀门位置.

为了得出最佳阀门位置的优化结果，首先需要模拟出管道安装阀门后的水力情况.由于管道上增加阀门相当于该管道增加了水头损失，因此可以采用虚拟阀门方法，即通过改变管道的粗糙系数或局部水头损失系数来模拟该管道上增加阀门的水力情况.

2.1.1目标函数

阀门最佳安装位置，本文定义为在管网中某些管道安装虚拟阀门(改变管道海森威廉系数或局部水头损失系数)后管网所有节点在一天中剩余压力的平方和的平均值之和最小.为了使装上阀门之后，整个管网的节点压力趋于稳定，目标函数如下:

(5)

式中：i为时段编号;j为管道编号;Hi,j为节点j在i时段的压力；Hr为最小服务水压；n为节点个数;k为时段数.

2.1.2约束条件

(1) 以管网连续性方程与能量守恒方程为基础的隐式水力平衡约束条件

(6)

(2) 整数约束

巢穴经过进化更新后(莱维飞行、巢穴更新)，部分巢穴中的解可能会变成非整数，既不符合实际情况，也无法计算该巢穴的适应度值.此时，需要调整步长控制量α，对该巢穴进行整数处理.

2.2第二层优化模型

通过上一层优化模型，可以知道管网中阀门的个数与最佳安装位置.在本层优化中，继续使用布谷鸟算法对每个时段的阀门的开启度进行优化.

在给水管网中常用的调压阀类型有①减压阀，限制管网下游的压力；②稳压阀，限制管网上游的压力；③流量控制阀，限制管道特定的流量④节流控制阀，通过调整阀门的局部水头损失系数，模拟半关闭的阀门.

2.2.1目标函数

给水管网阀门优化的最终目的是减少管网漏损量，因此本层优化的目标函数为

(7)

式中：i为管道编号;n为管网管道总数；QL,i为管道i的漏损量，计算如下[8]:

(8)

式中：Ci为漏损系数；Li为管道i的长度；Hi为管道i的平均压力.

2.2.2约束条件

(1) 以管网连续性方程与能量守恒方程为基础的隐式水力平衡约束条件同上层优化模型

(2) 最小服务水压约束

为了保证管网的最低用水需求与稳定性，节点压力不能小于节点最低需求压力.即通过减压阀调节后，管网中所有节点压力均在最小服务水压之上.

(9)

式中：i为节点编号;Hi∈Ωn，Ωn为节点集合；Hr为最小服务水压.

3算例研究

图2所示为参考文献[3]中的算例，共有22个节点与37条管道以及3个水源供水，具体节点信息见表1，水库信息见表2，管道信息见表3，管网时变化系数见图3.

图2　算例管网示意图

节点ID12345678910111213141516171819202122标高/m18181412141514.514141512152320810781071015需水量/L·S-151005301002005100052000550020

表2　水库数据

运用布谷鸟算法优化时，依据以往算法运行的经验，初始巢穴数量设为n=15，步长控制量设为α=1，位置参数设为β=1.5，发现概率设为P=0.25；计算漏损量的漏损系Cij取0.00001，最小服务水压Hr取30 m.

图3　算例管网时变化系数图

4结果分析

4.1不同阀门个数分析

图4展示了该管网分别在0,1,4个阀门的最优布置下各个时段漏损量的变化.从0个阀门这条曲线可以得知，管网在深夜时变化系数变小，流量减少、压力增大，则漏损量会增加.通过阀门的控制后，漏损的情况得到明显改善.

图4　漏水量时变化

表4展示了不同的阀门个数，在时变化系数为1时，最佳的安装位置，以及它们的虚拟开度和此时的漏损量.图5展示了不同的阀门个数在采用最佳控制后，该管网12个时段的平均漏损量对比图.

可以明显看出，管线11在减少漏损方面是一条非常重要的管线，仅在管线11 上装有阀门时，平均漏损降低13.66%.随着阀门数量的增加，漏损降低的幅度也逐渐减少，说明了阀门的位置比起阀门的数量在漏损控制方面更重要.

表4　阀门优化结果

图5　不同数量阀门平均漏损量

4.2算法比较

图6展示了在已知阀门位置时分别使用遗传算法(种群n=100、变异概率0.08、交叉概率0.75)和布谷鸟算法求解最优阀门开度所需进化代数对比.

当使用优化算法求解阀门最优化问题时，每一个种群在经历一代要调用一次管网平差软件进行水力计算.从图6可以粗略估算出，遗传算法到达收敛结果需要100个种群经历70代，调用7 000次管网平差软件.布谷鸟算法到达收敛结果仅需要15个种群经历53代，调用795次管网平差软件，极大地提升了计算速度.从图6可以看出遗传算法的曲线更加平滑，初始结果较好.这是由于遗传算法的初始种群100远大于布谷鸟算法种群数15，故遗传算法的初始结果较好.随着各自算法中种群的进化，遗传算法是随机搜索解空间而布谷鸟算法是通过莱维飞行以及巢穴更新机理依据当代最优解来自适应调整进化步长，并且布谷鸟算法中种群是各自进化产生子代而遗传算法中种群是相互作用产生子代，故布谷鸟算法较快收敛.基于此算例研究得出，布谷鸟算法定位寻找最优解效率更高，遗传算法寻找临近解表现稳定更具有效率.因此，当工程案例需要较为精确的模拟结果时，布谷鸟算法效率更高.当工程案例复杂仅需要模拟的初略结果作为实际操作指导时，遗传算法表现更好.

图6　优化算法速率对比

此外，在第一层优化模型中，利用布谷鸟算法确定阀门的最佳安装位置，对于不同数量的阀门，得到最优结果的平均代数约为20代左右.故在确定阀门数量的前提下，对阀门的位置以及开启度的优化仅仅只需要初始种群为15的情况下进化约90次即可，计算时间小于Ali和Mohammed E[5]提出的方法.

5结论

通过控制阀门来进行压力管理可以有效地降低管网剩余压力，减少管网漏损量.但一般对于真实管网，由于计算量过于庞大，无法通过最优化算法来确

定最佳阀门控制策略，只能根据工程师经验来确定.

在确定阀门最佳安装位置时，利用的虚拟阀门是改变管道的局部水头损失为一个具体的值，极大地提升了寻找阀门最佳安装位置的速度.同时采用了布谷鸟算法来求解控制阀门的优化问题.是因为阀门位置和开度的优化问题属于混合离散非线性最优化模型，布谷鸟算法具有概念简单、结构明晰、初始设置值较少、与优化问题本身契合程度高等特点.并且相比于传统的遗传算法，布谷鸟算法极大地提升了寻找最优解的计算速度，使得对真实管网通过最优化算法来确定最佳阀门控制策略成为可能.

参考文献:

[1]Lambert A. International report: water losses management and techniques[J]. Water Science Technology Water Supply, 2002, 2(4): 1.

[2]Germanopoulos G. A technical note on the inclusion of pressure dependent demand and leakage terms in water supply network models[J]. Civil Engineering Systems, 1985, 2(3): 17.

[3]Jowitt P, Xu C. Optimal valve control in water distribution networks[J]. Water Resource Planning Management, 1990, 116: 455.

[4]Nicolini M. Optimal location and control of pressure reducing valves in water networks[J]. Water Resource Planning Management, 2009, 135: 178.

[5]Ali, Mohammed E. Knowledge-based optimization model for control valve locations in water distribution networks[J]. Water Resource Planning Management, 2015, 141:1.

[6]Yang Xin-She, Suash D. Cuckoo Search via levy flights[C]// World Congress on Nature & Biologically Inspired Computing. Coimbatore: IEEE, 2009: 210-214．

[7]Araujo L, Ramos H, Coelho S. Pressure control for leakage minimization in water distribution systems management[J]. Water Resource Management, 2006, 20(1): 133.

[8]Germanopoulos G, Jowitt P. Leakage reduction by excess pressure minimization in a water supply network[J]. Civil Engineering Systems, 1989, 87(2): 195.

Optimal Valve Control in Water Distribution Systems Based on Cuckoo Search

TAO Tao， ZHANG Jun， XIN Kunlun， LI Shuping

(College of Environmental Science and Engineering， Tongji University， Shanghai 200092， China)

Abstract：In order to solve the growing leakage problem of the city water distribution systems, control valves were proposed to be installed in the pipeline to decrease the pipe pressure. An optimized model was established by means of Cuckoo Search to determine the effective numbers of valves and their location. A comparative study was made to show the difference between Genetic Algorithm and Cuckoo Search. The results show Cuckoo Search has a better performance in terms of searching speed and parameter requirement, which reveals the potential of the proposed optimization model for control valves in a real-life water distribution system.

Key words：water distribution systems; Cuckoo Search; leakage reduction; control valve optimization design

文献标志码：A

中图分类号：TP15

基金项目：国家自然科学基金(51478326)

收稿日期：2015—07—10

第一作者： 陶涛(1974—)，女，教授，工学博士，主要研究方向为给排水管网优化设计运行.E-mail: taotao@tongji.edu.cn