考虑有限转角下薄壁构件稳定理论及其应用

余少乐, 周　祎

(1． 同济大学 土木工程学院， 上海 200092； 2． 西南交通大学 土木工程学院, 四川 成都 610031)



考虑有限转角下薄壁构件稳定理论及其应用

余少乐1, 周祎2

(1． 同济大学 土木工程学院， 上海 200092； 2． 西南交通大学 土木工程学院, 四川 成都 610031)

摘要：为了解决传统稳定理论的两个力学缺陷，引入半切线转角矢量作为构件转角的变量，由二阶转动矩阵推导出梁单元的二阶位移表达式，并利用有限变形理论，得出构件位移与应变的非线性关系，通过Bernoulli平截面弯曲假定得出转角与侧移导数.运用薄壁构件稳定理论，推导出构件弯扭屈曲的总势能，证实了传统理论，解决了传统理论中的缺陷，能够适用各种边界条件和荷载条件下的弯扭屈曲分析.

关键词：非线性分析； 稳定分析； 薄壁结构； 半切线转角

1钢结构稳定分析

在薄壁钢梁的稳定理论上，存在传统理论和考虑中面非线性剪切应变能的新近理论.传统理论存在本身难以克服的理论缺陷，但几十年的使用中并没有通过试验发现其存在的问题，并且许多国家规范采用以它为依据的公式，例如我国《钢结构设计规范》[1](GB50017—2003).文献[2-3]的理论仍属于传统理论范畴，在推导上使得传统理论显得更加精致，但仍然有两个缺陷:限制了结构的变形规律，使得结构的位移和转动只能按一定的次序发生和发展;对截面转角θ的简化不一致.

考虑到在空间构件分析中，空间转动不是矢量, 不遵守矢量加法交换律.Argyris[4-6]对空间有限转动的矩阵表示做过探讨，还对与两个(或更多的)连续任意的转动等价的混合转动矢量作了研究.通过引入描述刚体转动位置的转动角位置矢量,定义了半切线转角矢量，此理论用于刚体绕正交轴两次有限转动的合成问题,解决了有限转动的角位移无法定义为矢量的问题.Kim M Y, Chang S P ，Kim S B，等[7-8]对半切线转角矢量的转动矩阵进行推导，得出罗德里格转角矢量和半切线转角矢量的转动矩阵都是正交的，两转动矩阵的一阶和二阶项是相同，而三阶项是不同的.结构几何非线性的有限元计算方法是目前工程分析中的热门问题，Bathe[9]进行了大量研究,建立了三维梁单元大位移、大转动、小应变的U.L.列式和T.L.列式分析方法.陈政清[10]以三维连续梁的虚功增量方程为基础，导出了三维梁大挠度问题内力分析的U.L.列式法,提出了新的几何刚度矩阵形式，改进了Bathe的非线性梁单元，从而减少了U.L.列式的计算时间.本文引入半切线转角矢量作为构件转角的变量，得到二阶转动矩阵，由此推导出梁单元的二阶位移，并利用有限变形理论，得出构件位移与应变的非线性关系，运用薄壁构件稳定理论，推导出构件弯扭屈曲的总势能，与传统理论得到的总势能相同，与已有文献中分析结果进行比较，表明使用本文的方法对参考文献中试验构件计算的值和试验值误差很小，能够取得很高的精度.

2传统稳定理论的缺陷

鄂国康[11]指出目前普遍采用的理论限制了结构的弯扭变形过程，使得变形过程受制于线位移和转角位移按一定的先后顺序产生.

根据截面转角产生的先后次序，横截面上任一点P(x,y)的位移大致可用两种途径求得:①横截面先绕原剪切中心轴转动θx，然后再分别绕剪切点的主轴分别转动-Uz,x，Uy,x.②横截面先绕剪切点的主轴分别转动-Uz,x，Uy,x，然后再绕原剪切中心轴转动.第一种途径的转动次序是θx，-Uz,x，Uy,x.第二种途径的转动次序是θx，Uy,x，-Uz,x.不同的转动次序所导出的P(x,y)点的位移也不同.

按照目前的理论，横截面先绕原剪切中心轴转动，再分别绕剪切点的两主轴分别转动得到的位移与横截面先绕剪切点的两主轴分别转动，再绕原剪切中心轴转动得到的位移并不相同.所以不同的转动次序所导出的位移也不同.这说明结构的屈曲是与转动次序有关的.实际上，屈曲过程是与转动的产生次序无关的，也就是说在屈曲的发生过程中各种转动是同时发生和发展的，并在该过程中相互作用.

童根树[12-13]指出传统稳定理论中截面中面上各点的位移与外荷载的位移对1-cosθ采用了不同数量级的简化.构件横截面上任一点P(x,y)侧向位移是采用1-cosθ≈0的简化而得到的，所以在求线性应变能和非线性的纵向应变能时也采用1-cosθ≈0，求非线性外力势能时却采用1-cosθ≈θ2/2的简化.在同一个理论中对1-cosθ采用了两种不同数量级的简化.

3半切线转角

对于大位移大转角问题,采用转角作为转动变量时,当质点绕固定坐标轴产生大转角转动时,其结果与转角施加顺序有关.因此,定义合理的转动变量至关重要[14].现有许多文献在基于协同转动法建立有限元公式时,因采用非矢量型转角而得到的单元切线刚度矩阵往往不对称,从而给结构整体刚度矩阵的存储和计算效率带来非常不利的影响.为避免因单元切线刚度矩阵不对称而带来的麻烦, Argyris定义了矢量型转动变量,将绕正交固定轴先后转动的角位置矢量记为θ1，θ2.合成的角位移矢量可表示为

(1)

(2)

其中，θ12，θ21为绕正交固定轴不同次序的转角.而半切线转角为这两不同次序转动转角的平均值.由此可知，半切线转角为转角矢量θ1，θ2之和，能像真正的矢量那样进行矢量的加法运算法则.参考文献[7]，设绕x，y，z轴的半切线转角分量为θx，θy，θz，其对应的转动矩阵为

(3)

该转动矩阵R具有以下几个特征：

(1)转动矩阵是正交的，即RTR=I.

(2)由于连续转动的半切线转角具有可交换性，所以转动矩阵与转动次序无关.

(3)由性质2可知，总势能方程具有唯一性.

4薄壁构件在有限转角下的稳定理论

本文采用的基本假定为: ①梁变形后横截面仍为平面; ②变形前后构件中线始终垂直于平截面；③忽略由翘曲引起y，z轴的曲率变化；④大变形，大转角，小应变；⑤弹性，均质，各向同性材料.

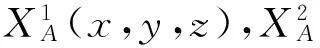
(4a)

(4b)

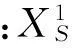
由式(4)可知，基矢量1ei和2ei的关系为

1ei=R2ei

(5)

A点的位移矢量UA可表示为

(6)

将式(4)和式(5)代入(6)，可得

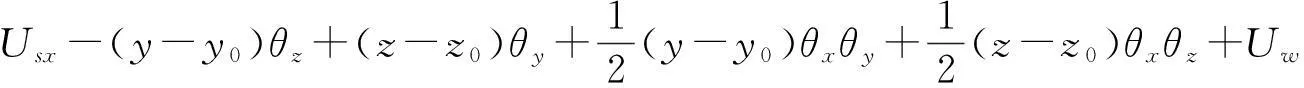
(7a)

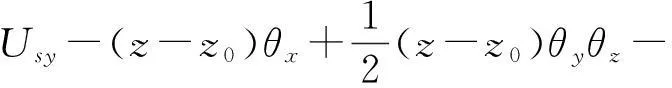
(7b)

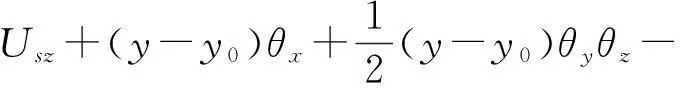
(7c)

其中，Usx,Usy,Usz分别是剪心S点关于x,y和z轴的刚体位移，如图1所示.

图1薄壁构件横截面的位移和力

Fig.1Force and displacement components of thin-

walled structure’s cross-section

采用有限变形理论分析构件的变形关系，应变与位移的关系为

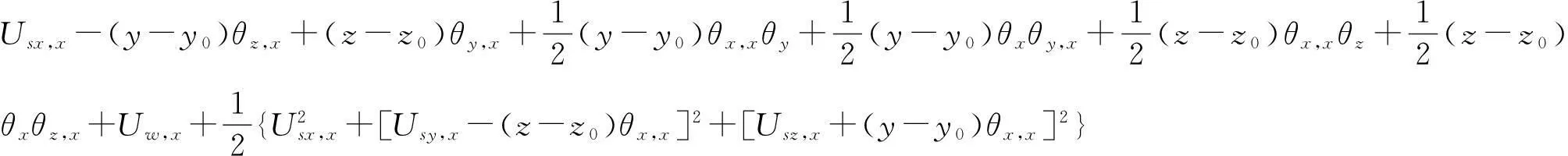
(8a)

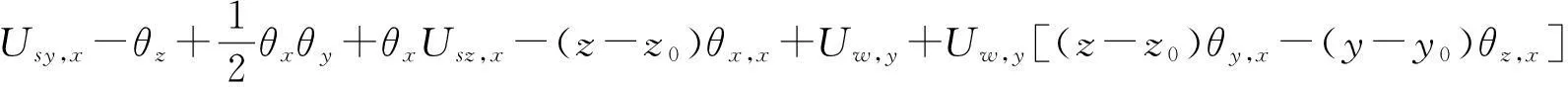
(8b)

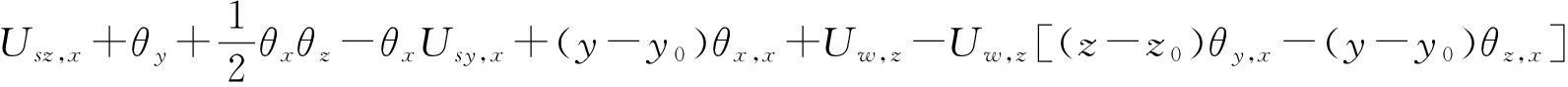
(8c)

在Vlasov基本假定中薄壁中面线性剪应变为零，本文中将薄壁中面线性剪应变为零的假定扩展到非线性范围，即

(9a)

(9b)

Uw,y-(z-z0)θx,x+Uw,y[(z-z0)θy,x-(y-y0)θz,x]=0

(9c)

Uw,z-(y-y0)θx,x+Uw,z[(z-z0)θy,x-(y-y0)θz,x]=0

(9d)

由式(9a)和式(9b)可知，转角与侧移导数的关系为

(10a)

(10b)

截面翘曲只考虑与y和z的线性关系，故忽略式(9c)中Uw,y[(z-z0)θy,x-(y-y0)θz,x]项和式(9d)中Uw,z[(z-z0)θy,x-(y-y0)θz,x]项，由式(9c)和(9d)可知

(11)

其中，ωs为剪心S点的扇性坐标.

以y=0,z=0代入式(7a)可得截面形心C纵向位移Ucx,即

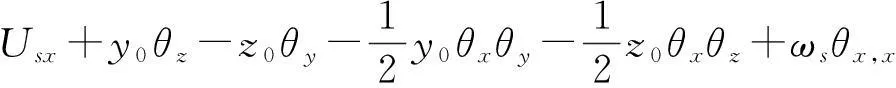
(12)

令Ux=Ucx+ωsθx,x，则式(7a) 可写为

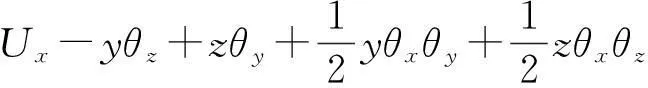
(13)

式(8a)又可以写为

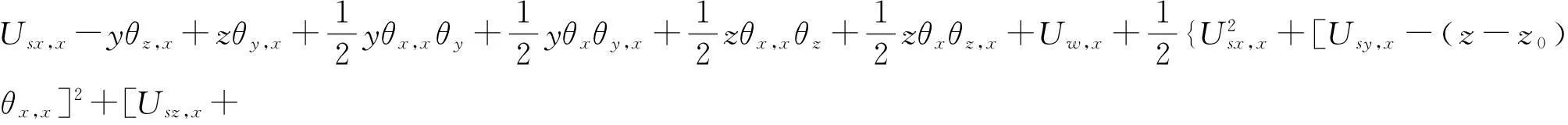
(y-y0)θx,x]2}

(14)

式(14)与文献[2]中式(17.163)，文献[3]中式(A2.12)给出的应变表达式是一致的.

将式(10a)，(10b)代入式(14)得

ε11=Ux,x-yUsy,xx-zUsz,xx+θxUsz,xx+ωsθx,x+

(15)

将式(9c)和(9d)代入式(8b)和(8c)可知

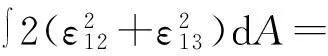
(16)

式中,J为截面抗扭常数.

J=∫[z2+y2+2zUw,y-2yUw,z+(Uw,y)2+(Uw,z)2]dA

(17)

5薄壁构件的应变能与荷载势能

薄壁构件应变能w由纵向应变能与剪切应变能组成如下：

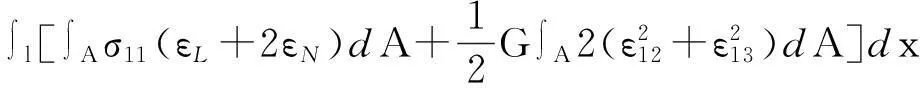
(18)

考虑截面的残余应力σr分布的影响，正应力σ11为

(19)

式中：A是截面面积;G是剪切模量；Iy,Iz,Iω分别截面对y，z轴的惯性矩，截面的主扇形惯性矩；P为构件轴力；My,Mz为构件对y，z轴弯矩；Bω为构件的弯扭双力矩.截面的正应力σ11除了有线性部分σL外，还有非线性正应力σN，故可得

(20)

如果忽略式(20)中的非线性部分的高阶项σNεN，且知σLεN=σNεL，由此可知

(21)

可写为

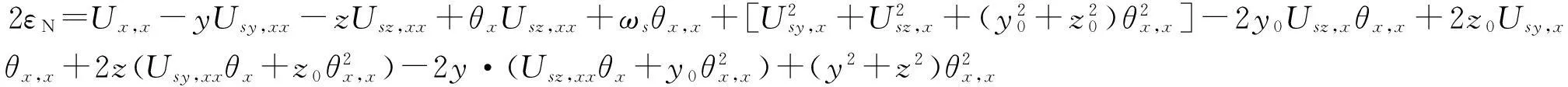
(22)

将式(16)和式(22)代入式(18)得构件的应变能

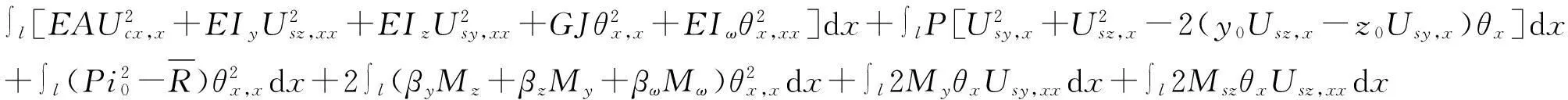
(23)

式中：Ucx为形心纵向位移；E为弹性模量.

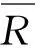
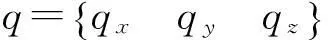
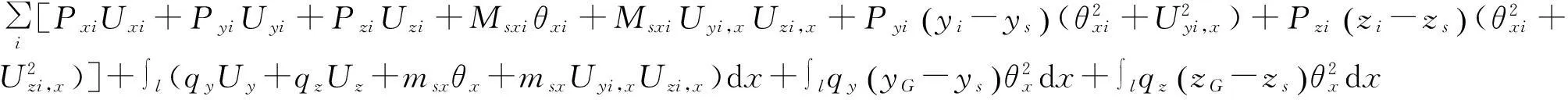
(24)

式中:Msx,msx分别为绕剪心的集中扭矩和分布扭矩.yG-ys，zG-zs表示横向均布荷载作用点至截面剪心之间的距离.yi-ys，zi-zs表示集中荷载作用点至截面剪心之间的距离.

半切线转角矢量作为转角位移，初始矢量的最终位置则与连续转动的次序无关，由推导出的转动矩阵，当转动轴的定义给定之后，不同的截面转动次序导致的结果仍然是一致的，这说明结构的屈曲是与转动次序无关的.截面上各点的位移与外荷载的位移均来自于式7a，式7b和式7c，纵向应变能与外力势能都采用了1-cosθ≈θ2/2的简化，不存在传统理论上的问题.

6薄壁构件的弯扭失稳

利用提出的总势能，对承受各种荷载的简支梁和悬臂梁的弯扭屈曲进行了分析.对于简支梁，其总势能与传统理论的表达式是一致的.采用伽辽金法，求得横向荷载作用时梁侧扭屈曲临界弯矩Mcr的一般表达式为

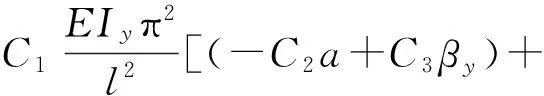
(25)

式中，a为荷载作用点与截面剪心的距离.系数C1,C2和C3见表1.

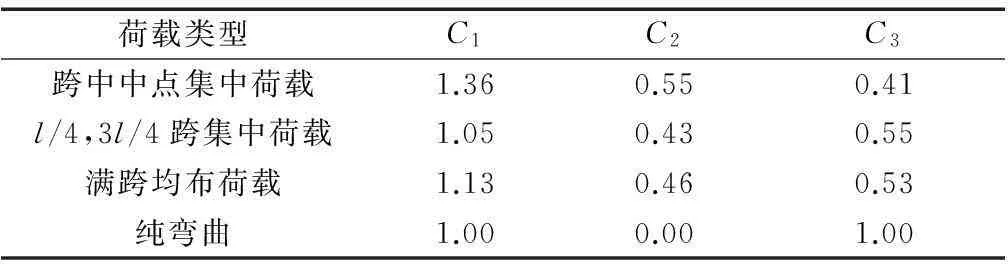
表1　在不同的荷载作用下的系数

悬臂梁承受均布荷载和自由端集中荷载时，总势能表达式为

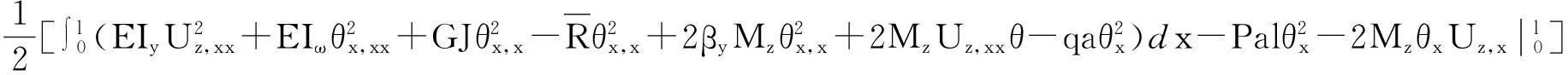
(26)

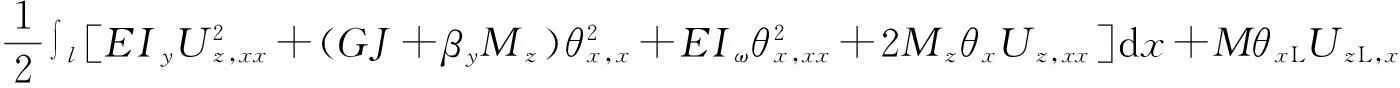
(27)

比传统理论的总势能多了最后一项，即边界条件项由势能驻值条件，取总势能的一阶变分为零，可得悬臂梁在纯弯下的边界条件和平衡方程，并与传统理论做比较，有着相同的平衡方程和固定端的边界条件，但自由端的边界条件有所不同.文献[2]为解决传统理论的缺陷，在传统理论的总势能中另加上所谓的“自由端弯矩在悬臂梁屈曲过程中的所做的功”：MθxLUzL,x，这样得到的总势能可以满足悬臂梁在屈曲过程变形中对自由端弯矩的转动要求.由于本文考虑了杆件位移的二阶性，故在荷载势能中出现了非线性项，自然保留了文献[2]所增加的项.

童根树提出了一种新的薄壁截面梁的弯扭屈曲理论，它的总势能由线性应变能，非线性纵向应变能，非线性剪切应变能和非线性横向应变能组成，对于悬臂梁在纯弯下的屈曲的总势能为

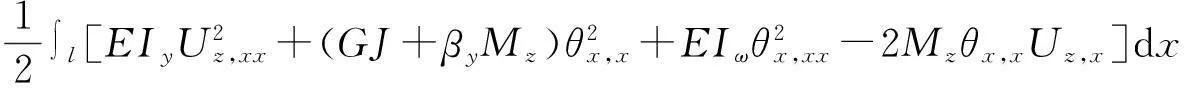
(28)

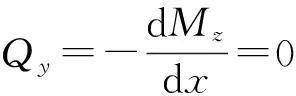
可以看出，童根树提出的悬臂梁在纯弯下总势能的形式可以回归到本文所提出理论的形式.

当自由端仅作用横向集中力时，因为自由端弯矩为零，传统理论与本文理论的总势能都为

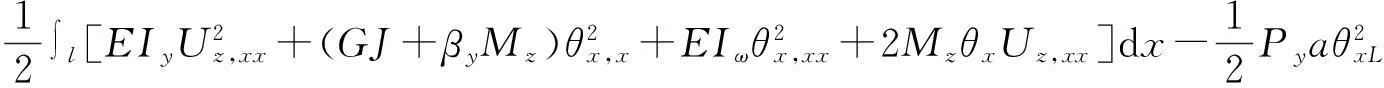
(29)

张磊和童根树利用有限元程序的计算，将每根悬臂梁分为30个单元，使用三次多项式的位移函数，用求特征值的方法来得到临界荷载.通过与文献[15-16]的试验结果相比较，由式(29)得到的临界荷载值，与试验值之间的误差基本在5%之内.

7结论

提出了考虑有限转角下薄壁构件非线性应变能的一般表达式，导出了弯扭失稳的总势能方程，克服了传统稳定理论存在的力学缺陷.由总势能的二阶变分推导的单元几何非线性切线刚度矩阵对钢结构稳定分析具有较高的精度和适用性.

参考文献:

[1]中华人民共和国建设部. GB50017—2003钢结构设计规范[S].北京：中国计划出版社，2003.

Ministry of Construction. GB50017—2003 Code for design of steel structures[S].Beijing: China Planning Press, 2003.

[2]Trahai N S. Flexural-torsional buckling of structure [M]. London: E & FN SPON, 1993.

[3]陈骥. 钢结构稳定理论与设计[M]. 2版. 北京: 科学出版社, 2003.

CHEN Ji. Stability of steel structures theory and design [M]. 2nd ed. Beijing: Science Press, 2003.

[4]Argyris J H, Dunne P C, Scharpf D W. On large displacement-small strain analysis of structures with rotation DOF[J]. Computer Methods in Applied Mechanics and Engineering, 1978, 14:401.

[5]Argyris J H, Hilpert O, Malejannakis G A. On the geometrical stiffness of abeam in space—a consistent V W approach[J]. Computer Methods in Applied Mechanics and Engineering, 1979, 20: 105.

[6]Argyris J H. An excursion into large rotations[J]. Computer Methods in Applied Mechanics and Engineering, 1982, 32: 85.

[7]Kim M Y, Chang S P, Park H G. Spatial postbuckling analysis of nonsymmetric thin-walled frames. I: Theoretical considerations based on semitangential property[J]. Journal of Engineering Mechanics, ASCE, 2001, 127 (8): 769.

[8]Kim S B, Kim M Y. Improved formulation for spatial stability and free vibrations of thin-walled tapered beams and space frames[J]. Engineering Structures, 2000, 22: 446.

[9]Bathe K J, Bolourchi S. Large displacement analysis of three dimensional beam structures[J]. International Journal for Numerical Methods in Engineering, 1979, 14: 961.

[10]陈政清,曾庆元,颜全胜.空间杆系结构大挠度问题内力分析的UL列式法[J].土木工程学报, 1992, 25(5): 34.

CHEN Zhengqing, ZENG Qingyuan, YAN Quansheng. A UL Formulation for internal force analysis of spacial frame structures with large displacement [J].China Civil Engineering Journal,1992,25(5):34.

[11]鄂国康. 关于结构弯扭屈曲理论的修正.应用数学和力学[J]. 1997, 18(10): 911.

E Guokang. Modification in the theory on flexural-torsional buckling of structures[J]. Applied Mathematics and Mechanics, 1997, 18(10): 911.

[12]童根树. 钢结构的平面外稳定[M]. 北京：中国建筑工业出版社，2006.

TONG Genshu.Out-plane stability of steel structure[M].Beijing:China Architecture & Building Press,2006.

[13]张磊. 考虑横向正应力影响的薄壁构件稳定理论及其应用[D]. 杭州：浙江大学，2007.

ZHANG Lei. A Theory of stability for thin-walled members considering the effects of transverse stresses and its applicatons. [D].Hangzhou: Zhejiang University.

[14]Attard M M, Bradford M A. Bifurcation experiments on monosymmetric cantilevers[C]∥12th Australasian Conference on the Mechanics of Structures and Materials. Brisbane: [s.n.], 1990: 207-213.

[15]Anderson J M, Trahair N S. Stability of mono-symmetric beams and cantilever[J]. Journal of Structural Division, ASCE, 1991, 98(1):269.

[16]Attard M M, Brdaoford M A. Bifurcation experiments on monosymmetric cantilevers[C]∥12th Australian Conference on the Mechanics of Structures and Materials. Sydney:[s.n.],1990:207-213.

Theory of Thin-walled Component Stability Based on Finite Rotation and Its Application

YU Shaole1， ZHOU Yi2

(1． College of Civil Engineering， Tongji University， Shanghai 200092，China; 2． College of Civil Engineering，Southwest Jiaotong University, Chengdu 610031, China)

Abstract：To overcome the default of the classic theory, semitangential rotation was introduced as the spatially rotational parameters. Based on the second-order rotation matrix, the expression of the second-order displacement of beam element was deduced. According to the finite deformation theory, the strain-displacement non-linear relationship for the thin-walled structures were presented. Based on the Bernoulli plain section assumption, the relation between rotation and transverse displacement derivative was derived. Thin-walled component stability theory was adopted to duduce the total potential energy of flexural-torsional buckling, which verified the traditional formula and overcame the defects of traditional theory. The analysis results show that the proposed theory is suitable for flexural-torsional buckling analysis of beams under any boundary conditions and loadings.

Key words：nonlinear analysis； buckling analysis； thin-walled structure； semitangential rotation

文献标志码：A

中图分类号：TU318

通讯作者：周祎(1982—)男，工学博士，讲师，主要研究方向为空间结构、非线性有限元理论.E-mail：suzhouzhouyi@163.com

收稿日期：2015—05—07

第一作者： 余少乐(1987—)男，博士生,主要研究方向为空间结构、预制装配式结构.E-mail:yushaole10@163.com