中国保险业资产配置与风险整合——基于虚实配比、Copula-CVaR模型和Monte Carlo算法的实证研究

王大鹏　赵正堂



中国保险业资产配置与风险整合
——基于虚实配比、Copula-CVaR模型和Monte Carlo算法的实证研究

王大鹏赵正堂

[摘要]我国整体杠杆水平低于发达国家平均水平，但近年来上升较快，这是个值得深入考察的现象。资本市场、银行体系乃至货币市场中任何一个部门的风险都有可能传递至实体经济。为此，通过构建Copula-CVaR模型，考察中国保险业资产配置的整合风险。根据债券、股票&基金、房地产和基础设施四类资产收益率之间的相关性，以Copula函数将各资产收益率的分布函数连接起来，运用Monte Carlo模拟测算我国保险资金投资比例下的CVaR值，以此衡量我国保险业资产配置的整合风险价值，同时研究最优CVaR对应的保险资产配置比例。实证结果表明：t-Copula函数较正态Copula函数能够更好地拟合我国保险业资产收益率状况，债券、股票&基金的投资比例增大会增加整合风险CVaR值；增加基础设施投资比例是可行的，但必须注意防范房地产价格上升掩盖的投资风险。

[关键词]保险业； 虚实配比； 资产配置； 风险整合； Copula-CVaR模型

一引言

2014年我国总债务为153.7万亿元，总杠杆水平为241%，低于发达国家359.15%的平均水平，尚处于温和可控的阶段，但我国债务水平近年来上升较快，2007年金融危机以来，总杠杆率上升了71%，其中金融企业部门总债务从1996年的2862亿元上升到2014年的14万亿元，增长了47.9倍，金融机构债务余额占GDP比重由1996年的4%上升到2014年的22%，上升了18个百分点。随着金融体系的不断培育和发展，资本市场、银行体系乃至货币市场相互关系越来越紧密，任何一个部门或市场的风险会迅速向其他部门蔓延，甚至会影响到实体经济和社会稳定。在此背景下，一向以稳健为原则的保险资金的整合风险研究意义重大(马建堂等，2016)[1]。

伴随利率市场化改革的推进，我国保险业快速发展。契合大资产管理时代的到来，保险业投资渠道全面拓宽，总资产规模快速上升，由2004年的不足1万亿元到2015年末的12.4万亿元，成为我国资本市场上仅次于银行和信托的第三大机构投资者。与证券、基金和信托等机构相比，保险业资产配置具有投资周期长、风险偏好低、资金成本合理、大类资产配置更加多元化等特征，有利于稳定证券市场，提高资产定价效率，是我国资本市场上最重要的机构投资者之一。2015年末，保险资产配置中，银行存款占比21.78%，债券占比34.39%，股票和证券投资基金占比15.18%，另类投资占比23.31%，其他投资占比5.34%。*本节的数据主要来源于保险资产管理业协会。保险业不仅有利于保障居民和社会的人身与财产安全，而且可以发挥保险资金长期投资和保险业风险保障的独特优势，支持重点工程建设，加强保险业对经济增长和机构调整的支撑作用。截至2013年末，美国寿险业总资产规模6.15亿美元，其中，债券占比48.78%，股票占比32.58%，抵押贷款占比6.08%，投资性房地产占比0.51%，政策性贷款占比2.14%，其他资产占比9.91%。*此处数据来源为Life Insurers Fact Book 2014，American Council of Life Insurers。从另一方面看，美国保险机构投资基础设施产品形式较多。在全球去杠杆化、金融脱媒和巴塞尔协议Ⅲ的影响下，银行体系中长期资金供给和需求在时间、数量上的不匹配，养老金、保险资金和主权财富基金等机构投资者逐步成为基础设施投资的直接资金供给方。与银行、证券、信托等其他金融部门相比，保险业可以提供期限更长、供应更加稳定、资金成本较为合理的巨额资本，有条件成为经济新常态下长期投资资金的重要来源之一。《加快现代保险服务业发展意见》(新国十条)发布后，保险资金不断增强支持实体经济的力度，截至2015年末，各类保险机构累计发起设立各类基础设施债权投资计划、基础设施股权投资计划和项目资产支持计划499项，合计注册规模1.3万亿元。虽然保险机构对基础设施的投资快速发展，但也面临着诸多问题，例如：监管政策立法层级有待进一步提升；高度依赖外部增信，存在一定风险隐患；投资管理能力需要提高等。

受外部金融市场环境不稳性的影响，保险资产配置面临着前所未有的复杂风险环境，资产配置的稳健性是检验保险业抵抗风险程度强弱的因素之一。保险资金运用风险管理越来越受到学术界、保险公司及监管机构的重视。卞世博和刘海龙(2013)[2]研究了随机利率条件下投资者在可违约债券、国债、股票以及银行存款之间的最优资产配置问题，将利率风险和跳跃风险同时引入资产组合并揭示了利率风险溢价和跳跃风险溢价与最优资产组合之间的关系。田玲等(2015)[3]运用GARCH 模型和GJR 模型，并结合Copula 理论，探讨了投资风险限额配置的方法，通过实证分析证实投资组合之间存在分散化效应，各投资风险限额之和大于总风险限额，并得出根据投资风险限额优化配置模型调整资产配置可以显著提高保险公司投资绩效。

风险管理一直是保险公司运营的关键性问题，资金的安全性也是资产配置的首要问题，如何准确度量整体风险、合理进行资产配置对于维持保险公司偿付能力和承保能力至关重要。因此，科学的风险度量方法和可靠的资产配置方式有利于提高保险行业风险管理水平，促进保险业健康稳健发展。传统风险研究多将金融资产间的相关性假设为线性相关，单个金融资产满足独立性和正态性特征，所以多个风险源构成的整体风险可以通过简单加和得到多元正态分布描述。然而，现实中的金融风险复杂多变，呈现非线性和尾部相关的相关结构，单个金融资产收益率分布具有尖峰、厚尾等非正态特征，基于线性相关的分析方法已经不能准确反映金融资产间的交互影响，因此实证结果通常与实际情况相差较大。为准确度量投资组合整体风险价值，须充分考虑金融资产间的复杂相关关系和单个资产收益率的分布特征。

Copula函数作为相关性分析和多元统计分析工具，能够很好地解决多元金融时间序列建模问题，它不仅可以刻画资产间的非线性相关关系，而且对边缘分布没有任何限制，在不确定边缘分布的具体形式时，通过直接采用各变量的经验分布函数，可以减少因边缘分布假设带来的误差。Copula函数最早由Sklar(1959)[4]提出，即可以将多个边缘分布通过一个Copula函数连接起来形成多元分布函数。Klugman(1999)[5]利用Q-Q图检验二元Copula函数的拟合优度，认为此函数具有较好的判别效果。Embrechts et al.(1999)[6]首次将Copula函数应用在金融风险管理领域，系统地研究了基于椭圆族和阿基米德族Copula函数的风险资产相关性，并计算出股票投资组合市场风险。McNeil和Frey(2007)[7]利用Copula函数尾部相关性的特点进行研究，强调风险边缘分布的尾部分布的重要性。

越来越多的国内外学者将Copula模型与Monte Carlo模拟、VaR理论、GARCH模型等结合起来，进行更加细致深入的分析。Romano和Clemente(2003)[8]研究了意大利股票市场，运用极值理论确定Copula函数的组合风险因子收益率，并通过Monte Carlo模拟计算资产投资组合的VaR值，结果表明基于极值理论的Copula模型优于多元正态分布假设下的VaR模型。Rosenberg和Schuermann(2004)[9]利用Copula函数研究商业银行的市场风险、信用风险和操作风险整合问题，并与其他风险度量模型进行比较，结果表明由Copula模型计算得到的VaR值与经验VaR最接近。Jondeau和Rockinger(2006)[10]考虑到样本数据可能存在的自相关与异方差等特征，利用GARCH模型得到变量边缘分布，再结合多种Copula函数，建立Copula-GARCH模型研究金融指数之间的相关性，发现t-Copula能较好地描述风险资产间的相关结构。白保中等(2009)[11]基于Copula函数度量银行资产组合信用风险，通过建立银行资产组合中每个资产的收益率门槛值，模拟资产收益率情景，得到各个假设状态下Copula函数度量的资产组合信用风险。实证证明，t-Copula可以较好地拟合商业银行资产金融状态。Fengge et al.(2013)[12]利用极值理论和CVaR模型，在95%和99%的置信区间下对中国商业银行操作风险进行了实证分析和数值模拟，取得了良好的效果。

Copula函数也被越来越多地应用到保险行业的整合风险度量中。Ward和Lee(2002)[13]利用正态Copula函数对保险行业中的不同风险进行整合，研究了保险公司的总体风险分布情况。梁冯珍等(2006)[14]利用对数正态分布作为各保险业务赔偿额的中部和左尾部的分布，用广义Pareto 分布作为赔偿额的右尾分布，用t-Copula函数描述业务之间的相关性，随机模拟结果表明，用该种方法确定的准备金要比传统上确定的准备金至少节约10%的资金。陈辉和陈建成(2008)[15]选用沪深300指数、基金指数、企债指数和国债指数4种风险资产来模拟保险投资组合中的股票、基金、企债和国债收益，分别采用传统近似方法和Copula方法计算投资组合的总风险，结果表明H-VaR相对于Copula-VaR是一种比较保守的方法，且投资组合权重变化和Copula函数的选择对投资组合总风险产生影响。

VaR模型最早是20世纪90年代J.P.Morgan公司在实际风险管理的过程中使用并且逐渐完善的。Artzner et al.(1999)[16]提出一致性风险度量原理，指出VaR模型不满足次可加性的缺陷，提出了更加合理的尾部条件期望，CVaR模型由此产生，由此该模型开始广泛被运用于金融保险领域。

国内关于整合风险的研究多集中在股票市场投资组合和商业银行方面，研究保险业整合风险的文献较少。既有文献中研究对象多以两种资产为主，多种资产的研究则以数据模拟为主。本文将研究对象扩展到4种资产，通过Copula函数研究其收益率的相关关系，并利用Monte Carlo模拟方法计算CVaR值以衡量保险业资金运用的整合风险。

后续内容安排如下：第二部分是基本模型介绍，介绍Copula-CVaR模型的基本原理，并且简单论述了模型的优点；第三部分基于Copula-CVaR函数进行实证检验，选取2011-2013年保险业的资产配置数据，进行整体风险评估，并且求解最优资产配置比例；第四部分是研究结论，首先分析模型适用性，然后结合目前保险业资产情况和最优资产配置比例给出建议。

二基本模型

(一)Copula函数及Sklar定理

Copula函数最早可以追溯到1959年的Sklar定理，该定理说明了联合分布函数可以拆解成为相应个数的边缘分布函数和唯一的一个Copula函数。Copula函数也可以理解为根据一定的相关关系，将所有边缘分布函数整合成联合分布函数的一个连接工具，因此Copula函数也被称为连接函数。一个N元Copula函数是指具有以下性质的分布函数C：定义域为[0,1]N，边缘分布为均匀分布；C的边缘分布Cn(un),un∈[0,1],n=1,2,…N满足C(1, …, 1,un, 1, …1)=un；对于所有的元素un,n=1, 2, …N,C(u1, …uN)是递增的。

Copula函数的Sklar定理：令F(·,…, ·)为具有边缘分布F1(·),F2(·), …,FN(·)的联合分布函数，则存在一个Copula函数C(·, …, ·)，满足：

F(x1, x2, …, xN)=C(F1(x1), F2(x2), …, FN(xN))

(1)

如果F1(·), F2(·), …, FN(·)是连续的，那么C(·, …, ·)唯一存在；反之，如果函数C(·, …, ·)为相应的Copula函数，F1(·), F2(·), …, FN(·)为一元分布函数，那么F(x1, x2, …, xN)是具有边缘分布函数为F1(·), F2(·), …, FN(·)的联合分布函数。由Sklar定理就可以在不研究联合分布函数的情况下，依然能通过Copula函数得到变量间的相关关系，这样就简化了求解联合概率分布的过程。Copula函数作为描述变量相关关系的连接函数虽然绕开一些求解困难，但是由于其求解参数比较复杂，需要借助编程手段进行参数估计，而且变量越多Copula函数的复杂度就越高，增加实际运用的困难。

常用的Copula函数包括两类：椭圆族Copula函数和阿基米德族Copula函数。椭圆族主要有正态分布Copula函数与t-Copula函数；阿基米德族主要有Gumble Copula函数、Clayton Copula函数和Frank Copula函数。椭圆Copula函数是一系列具有椭圆轮廓分布的函数，其主要优势是可以运用于不同相关程度的分布函数。阿基米德Copula函数克服了椭圆Copula函数计算复杂的特点，计算简单，容易捕捉尾部风险，但是不适合处理多变量的情况。此外，还有一些比较不常见的Copula函数，如多项式Copula函数，由于其在参数估计方面比较困难，因此不予考虑。

(二)CVaR模型的含义及优点

最常见的风险度量模型是VaR(Value at Risk)模型，VaR表示在正常的市场条件下，在给定的时间长度和置信度水平下，测算投资组合的最大损失值，也就是预期损失的分位数。VaR模型简单易懂，但是却不完全符合实际投资情况，存在较大的缺陷。因此本文引进CVaR模型，提高测算的准确度。

CVaR[X;P]=E[X|X≻VaR[X;P]]

(2)

CVaR模型被广泛运用在金融风险度量上，且在一定程度上克服了VaR模型的缺点，比如VaR违反了一致性公理中最重要的次可加性，VaR对损失分布的尾部损失信息反映不充分，没有给出最坏情形下的损失，VaR模型结果会受到样本变化的影响，且采用不同的统计方法会导致不同的VaR值，存在模型风险等。CVaR模型不仅考虑了损失超过VaR值的概率，还考虑了超过VaR值损失的条件期望，有效地改善了VaR模型在处理损失分布时存在的厚尾现象问题。当损失的密度函数是连续函数时，CVaR模型是一个一致性风险度量模型，具有次可加性和凸性。

(三)Copula-CVaR模型建模步骤

第一步：描述样本的数据特征，对样本数据进行正态性和相关性检验，确认样本数据可以使用；第二步：拟合变量的边缘分布函数，并对拟合结果进行检验；第三步：估计Copula函数的参数，构建完整的正态Copula函数和t-Copula函数模型；第四步：利用K-S统计量和P值检验Copula函数拟合效果；第五步：基于已获得的Copula函数，采用Monte Carlo模拟计算VaR值与CVaR值，获得当前保险业资产配置的整合风险情况；第六步：利用最优化的思路，调整优化目标，运用Monte Carlo模拟，求得最小整合风险价值的最优资产权重。

三基于Copula-CVaR模型的保险业整合风险计量

整合风险一直是金融保险领域风险管理的关键性问题。由于现实情况下，各个资产的收益率的分布不一定符合正态分布，而且收益率之间的相关性也极其复杂，这为衡量整合风险带来了许多困难。基于这种情况，下文将通过构建Copula-CVaR模型，考察保险业各投资资产收益率之间的相关性，由Copula函数将各资产收益率的分布函数连接起来，衡量我国保险业资产配置的整合风险，并且研究我国保险业最小整合风险下的最优资产配置权重，为保险公司提供参考。

(一)样本数据选取与处理

保险公司投资资产分为流动性资产、固定收益类资产、权益类资产、不动产类资产和其他金融资产等五大类资产。由于银行存款和流动性资产的信用风险、利率风险和操作风险等较低，因此未将上述两类资产纳入模型分析。由于股票和基金的收益率表现具有较大相关性和相似性，因此将股票和基金通过加权方式归为一类资产进行分析。由于其他另类投资占比较小，其他金融资产中以基础设施投资为主。本文研究对象为债券、股票&基金、房地产和基础设施，研究指标为上述四类资产的收益率。

选用2011-2013年保险业资产投资于债券、股票&基金、房地产以及基础设施的月度收益率及月度资产配置余额数据，样本容量为36。首先，为剔除奇异值对模型分析的影响，采用6个月移动平均法进行数据处理。其次，对债券、股票&基金、房地产及基础设施月度收益率进行年化处理。最后，对上述资产收益率进行风险调整，分别减去一年期国债收益率和五年期AAA级企业债收益率，得到最终的4个变量。本文采用Matlab2010a、Eviews和R软件进行数据描述和模型实现。

(二)样本数据描述

1.各收益率分布正态性检验

构造Copula函数之前需要确定四类资产收益率的边际分布，其基本统计特征如表1所示。从表1中可知，风险收益率波动最大的资产是股票&基金，其风险是最大的；而波动性最低的资产是房地产，其风险较小。从均值和中位数的角度来看，平均而言，房地产可以为保险业提供最大的收益率。但是从目前我国的实际情况来看，由于房地产价格一路飙升，没有发生大的跌幅，未来对于房地产的投资还是要采取较为谨慎的态度。

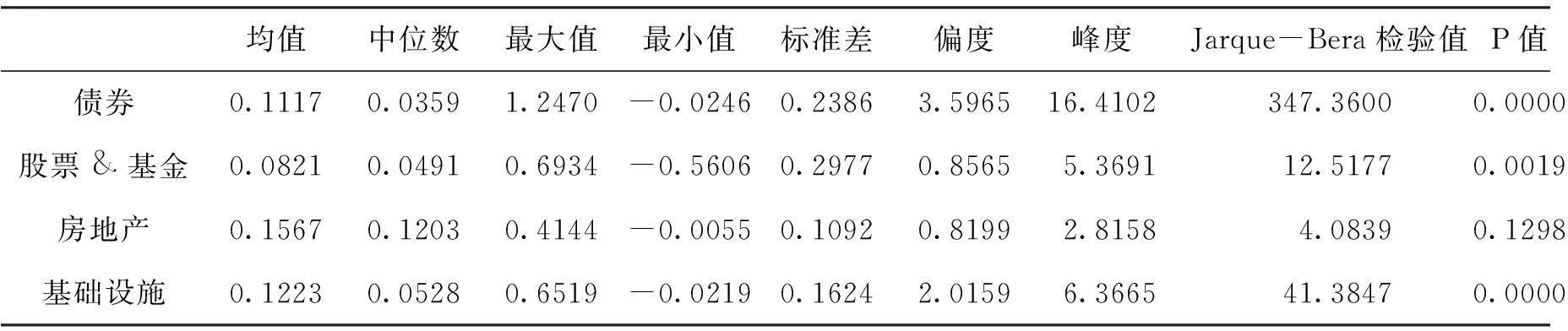
表1　风险收益率的基本统计特征

从Jarque-Bera统计量值看，债券、股票&基金和基础设施投资收益率的JB值较大，相应P值小于1%的显著性水平，拒绝原假设，表现为较明显的非正态性。而投资性房地产收益率的JB值为4.0839，P值超过10%，在90%的置信水平下不能拒绝原假设，认为投资性房地产收益率具有正态性特征。从直方图看，债券收益率与基础设施投资收益率呈现右偏特点，股票&基金收益率与投资性房地产收益率的正态性特征较突出，印证了股票&基金收益率的JB值偏小以及投资性房地产收益率的JB检验结果。

从Q-Q图可以得到与直方图和JB检验相同的结论，债券收益率和基础设施投资收益率明显表现出非正态性，股票&基金收益率表现出一定程度的正态性特征，投资性房地产收益率Q-Q图中的直线近似成45度角，正态性特征较显著。由于4种资产收益率中3个表现为非正态性，本文采用样本的经验分布作为变量的边缘分布，减少因边缘分布假设带来的误差。

2.各收益率数据相关性检验

Copula函数克服了传统线性相关系数关于样本假设的不足，样本数据不必服从正态分布，并且方差也不必一定存在。而且现实世界中的资产收益率间的关系并非线性相关，所以Copula函数提供了一种灵活的相关关系分析方法。由此，资产收益率之间存在一定的相关关系就是Copula函数运用的充分条件之一，构建模型前必须进行检验。

为确定四类资产的相关性，分别采用Pearson相关性检验、Spearman秩相关检验和Kendall秩相关检验，结果如表2所示。研究发现四类资产之间存在正相关关系，其中债券和基础设施的正相关性较强，其次债券与股票&基金、基础设施与房地产也存在一定的正相关性，房地产与股票&基金的相关关系不显著。

表2　相关系数矩阵

(三)边缘分布估计

由前述四类资产收益率数据特征可以看出，仅投资性房地产收益率近似服从正态分布，其余三类资产收益率分布均表现出不同程度的非正态性，也符合资产收益率通常表现出的尖峰、厚尾、非对称特点，而很多文献选取的对数正态分布、帕累托分布或者伽马分布拟合边缘分布会产生分布假设误差，因此本文采用样本数据的经验分布作为各资产收益率的边缘分布，能更准确地反映收益率分布的真实性，增强实证结果的可靠性。本文采用核密度估计，以最优窗宽和高斯核函数对边缘分布进行拟合。

下图为运用Matlab2010a软件得到的四类资产收益率的估计分布函数与样本分布函数对比图。

图1　债券收益率的经验分布

图2　股票&基金收益率的经验分布

图3　投资性房地产收益率的经验分布

图4　基础设施收益率的经验分布

从边缘分布图可以看出，投资性房地产收益率的边缘分布与正态分布非常相近，与上述的正态性检验结果相符，债券收益率与基础设施收益率的边缘分布形状较近似。

(四)Copula函数估计与检验

选取正态Copula函数和t-Copula函数描述四类资产收益率之间的相关结构，即得到能够反映整合风险的四元联合分布函数。对上述两种Copula函数的参数估计，采用K-S检验比较各连接函数的拟合优度。

K-S检验方法是通过样本的经验分布函数和标准分布函数来构建K-S统计量，只要这两种分布函数之间的差距小于给定距离，就可以认为样本是来自于总体，其分布服从于总体分布。该检验方法适用于连续型随机变量，K-S统计值越小，检验结果越显著。

表3　两种Copula函数的K-S检验结果

根据K-S检验结果，t-Copula函数的K-S检验统计量较小，相应的P值较高，所以t-Copula拟合效果略优于正态Copula，但两者拟合程度相差不大，P值均明显大于5%，在95%的置信水平下，在统计意义上无法拒绝其中任何一种Copula函数为真，因此下文将对两种Copula函数都利用Monte Carlo模拟计算整合风险的VaR值与CVaR值。

(五)基于Monte Carlo算法的整合风险价值计算

基于已估计得到的边缘分布和连接函数，计算整合风险价值还需要四类风险资产的权重。首先，以2013年末我国保险业投资于这四类资产的实际资产配置余额为权重计算整合风险的VaR值与CVaR值；然后，设定Monte Carlo模拟10000次计算最小CVaR值对应的各资产权重。

按照2013年末我国保险业资金投资于债券、股票&基金、房地产以及基础设施的资产配置比例，在99%、95%及90%的置信度下整合风险VaR值与CVaR值如表4所示：

表4　基于当前我国保险业投资比例的整合风险价值

相同置信水平下，正态Copula与t-Copula估计的整合风险CVaR值均大于VaR值，这符合CVaR值与VaR值的定义。随着置信水平的提高，整合风险价值也随之增加，但增加幅度并不大，说明我国保险业投资资产收益率的厚尾性不十分显著。

四基于Copula-CVaR模型的最优资产配置比例

(一)资产权重对整合风险价值的影响

将置信水平固定在99%，且保持前文Monte Carlo模拟次数10000次不变，考虑不同资产权重下整合风险CVaR值的变化。采用控制变量法进行研究，即保持其中两类资产权重不变，分析另外两类资产权重变化对CVaR值的影响*为保持内容的简洁性，避免过于冗余，仅列出两种情况下的CVaR值变化表格，其他情况下的表格，如有兴趣，可向作者索取。。

保持投资性房地产与基础设施的权重25%不变，将债券与股票&基金的权重以10%为间距，从0%到50%分别计算正态Copula和t-Copula连接函数下的整合风险CVaR值。随着债券资产比例增加，整合风险价值不断降低；而随着股票&基金的权重增加，整合风险价值不断增加。并且，根据t-Copula函数计算的整合风险价值均大于正态Copula得到的结果。债券的风险要低于股票&基金的风险，所以当资金投资于债券的比重较大时，将降低整个组合的风险。若仅考虑债券与股票&基金两类资产，则最优资产组合为单一债券资产的组合。

保持股票&基金与基础设施的权重25%不变，将债券与投资性房地产的权重以10%为间距，从0%到50%分别计算正态Copula和t-Copula连接函数下的整合风险CVaR值。研究结果显示，随着债券投资比例增加，整合风险价值不断增加；随着投资性房地产的投资比例增加，整合风险价值不断降低。t-Copula计算得到的CVaR值在每一投资比例下均大于正态Copula的结果，但相同程度的权重变化，CVaR值变化幅度明显比上一类资产小。若仅考虑债券与投资性房地产两类资产，最优组合理论上应全部由投资性房地产构成。

保持股票&基金与投资性房地产的权重25%不变，将债券与基础设施投资的权重以10%为间距，从0%到50%分别计算正态Copula和t-Copula连接函数下的整合风险CVaR值。随着债券投资比例增加，整合风险价值随之增大；随着基础设施权重增大，整合风险价值呈现下降趋势。等权重变化带来的整合风险CVaR值变化不大。若仅考虑债券和基础设施两类资产，则全部投资于债权投资计划(基础设施)可以达到最优组合。

保持债券与基础设施的权重25%不变，将股票&基金与投资性房地产的权重以10%为间距，从0%到50%分别计算正态Copula和t-Copula连接函数下的整合风险CVaR值。股票&基金的权重越大，投资性房地产权重越小，整合风险的价值越大，且变化较显著。若仅考虑股票&基金与投资性房地产两类资产，则应全部投资于投资性房地产从而达到最低整合风险。

保持债券与投资性房地产的权重25%不变，将股票&基金与基础设施投资的权重以10%为间距，从0%到50%分别计算正态Copula和t-Copula连接函数下的整合风险CVaR值。随着股票&基金投资比例增加，基础设施权重减小，正态Copula与t-Copula计算得到的整合风险价值增大。若只考虑此两类资产，全部资金投资于基础设施为最优。

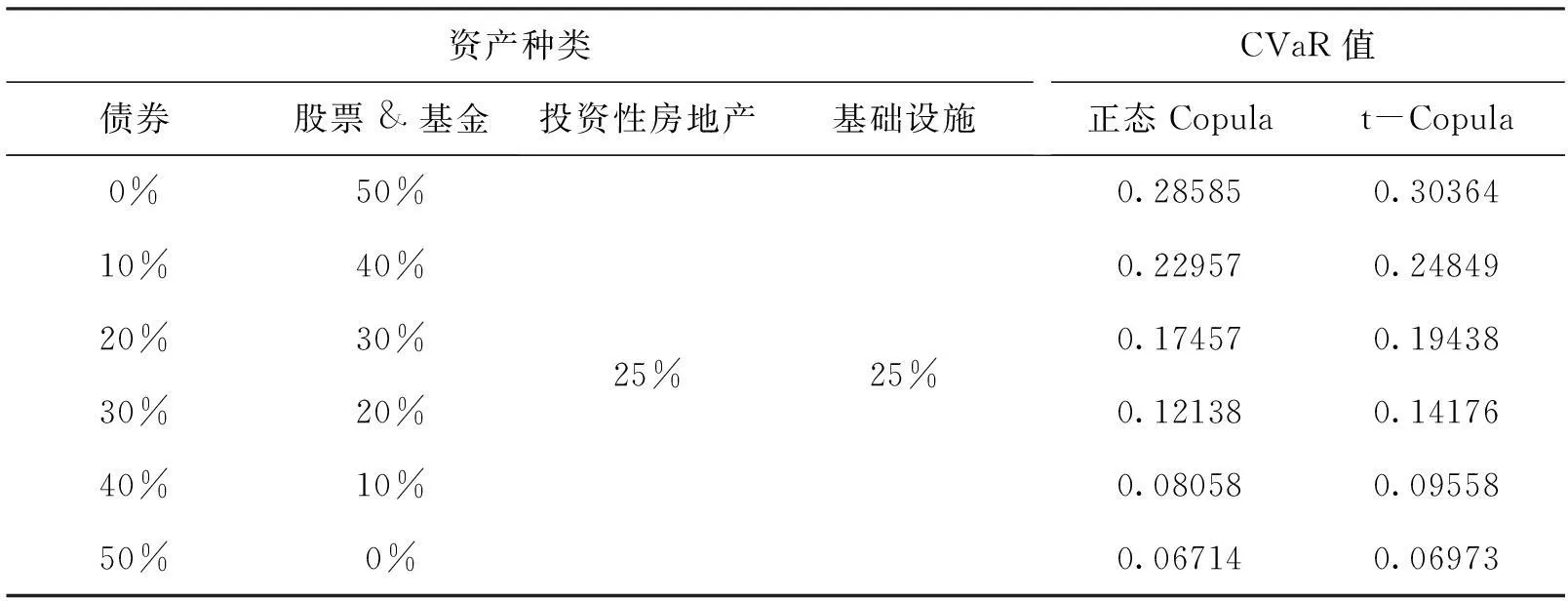
表5　债券与股票&基金的权重变化对整合风险价值的影响

表6　债券与投资性房地产的权重变化对整合风险价值的影响

保持债券与股票&基金的权重25%不变，将投资性房地产与基础设施以10%为间距，从0%到50%分别计算正态Copula和t-Copula连接函数下的整合风险CVaR值。研究结果显示投资性房地产投资比例越高，基础设施投资计划权重越低，整合风险价值越小，此两种资产权重变化对整合风险CVaR值影响显著性较差。若只考虑投资性房地产与基础设施投资计划，则最优投资方式为全部投资于投资性房地产。

总结资产权重对整合风险价值的影响可以得到以下结论：“两两资产比较结果”反映了保持另外两种资产投资权重不变的情况下，以最小整合风险CVaR值为标准，作为观察对象的两类资产被纳入最优组合的次数。相同额度的资金投资于投资性房地产对降低整合风险贡献最大，其次是基础设施和债券，而股票&基金将导致整合风险显著增加。债券投资风险小于投资性房地产和基础设施，因此债券投资比例增加应降低整合风险价值，但实证结果显示，除了与股票&基金比较研究时符合一般理论，当债券与投资性房地产及基础设施作为可选择资产时，均没有选择债券，原因是2011-2013年我国寿险业资金运用的债券月度收益率数据波动较大，从直方图数据也可以看出，债券、股票&基金、投资性房地产及基础设施投资计划的收益率标准差分别为0.2386、0.2277、0.1092与0.1624，且债券收益率的偏度和峰度也在四类资产中最大。

(二)基于最小整合风险价值的最优资产权重

以最小整合风险CVaR值为目标函数，各资产的边缘分布以及Copula连接函数为约束条件，运用Monte Carlo模拟方法，在99%的置信水平下考虑这四类资产的情况时，分别模拟10000次与1000次得到的资产最优权重如下表所示。

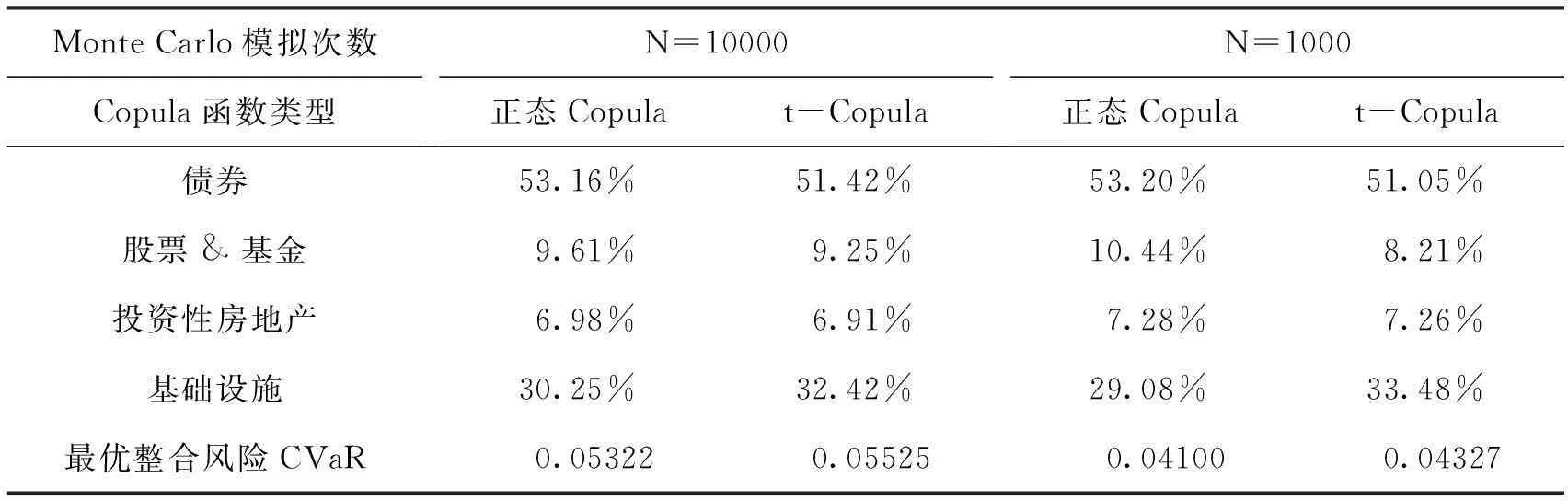
表7　最优组合投资比例与最小CVaR值

首先，正态Copula函数与t-Copula函数的实证结果差异不大。从最优资产组合构成上看，基础设施投资与债券投资占比超过83%。如果考虑到其他几类资产，最优投资策略应该是增加债券投资、基础设施投资的比例。

其次，t-Copula函数的模拟结果较正态Copula稳定。比较模拟次数为10000次与1000次的实证结果可以看出，t-Copula函数的最优权重估计值变化较小。另外，随着模拟次数增大，基础设施投资对最优资产组合的重要性越突出。

最后，股票&基金对最优组合整合风险的影响突出。即当股票&基金的投资比例减小时，整合风险价值显著降低。近期市场剧烈的波动，也显示出股票和基金对资产组合整合风险的影响较大。

总的来说，总体最优化的结果和“两两资产比较结果”得到的资产配置顺序存在一定差异。“两两资产比较结果”的情境下，保持两种资产权重不变，以最小整合风险CVaR值为标准，考虑另外两种资产被纳入最优组合的优先顺序：相同额度的资金投资于投资性房地产对降低整合风险贡献最大，其次是基础设施和债券，而股票&基金将导致整合风险显著增加。而最终最小化CVaR值得到的资产配置比例却是债券规模高于基础设施项目，而股票&基金和房地产位列最后。这是由于局部最优化结果和总体最优化不一定一致，考虑的维度不同得到的结论也不一样。

五结论

通过保险业资产配置状况可以发现，保险业资金大多分布于银行、证券市场、债券市场、房地产市场和实体经济中，与国民经济的方方面面相衔接，任何一个领域的风险可以迅速的传导至保险行业，同时各类风险经过保险行业也可以迅速传导至其他行业和整体宏观经济中。

本文通过构建Copula-CVaR模型研究我国保险业资产配置的整合风险，将传统研究的二元Copula函数拓展到四元，使研究结果更能反映保险业投资资产的实际情况。运用Monte Carlo模拟方法计算整合风险价值，采用控制变量法考察资产权重对整合风险价值的影响，同时运用VaR和CVaR度量整合风险价值，从分位数和尾部平均值两个角度描述整合风险特征，比较我国保险业资产投资于上述四类资产比例与模型的理论最优资产权重，得出以下结论：

(一)检验证实了t-Copula函数较正态Copula函数能够更好地拟合我国保险业投资资产收益率状况，且在不同测度下，t-Copula函数测算的整合风险价值(VaR值或CVaR值)普遍高于通过正态Copula函数得到的结果。当模拟次数由1000次增至10000次，t-Copula函数计算的整合风险价值也表现出较好的稳定性。但实证结果没有反映出t-Copula与正态Copula拟合效果的显著差异，各测度水平下的整合风险价值相差较小。

(二)债券与股票&基金的投资比例增大会显著增加整合风险CVaR值。通常认为，债券的投资风险较小，房地产投资的风险较大，得出上述结论的原因为我国股票市场和债券市场波动较大，而房地产市场处于快速上升阶段，未出现明显的价格下降，因此房地产市场所承担的风险被价格持续上升的表象掩盖。

(三)根据基于最小整合风险价值的最优资产权重的测算，对比我国当前保险业资产配置的现状，在研究模型假设的前提下，最优的投资策略为增加基础设施投资和房地产投资的比重。考虑到中国人口老龄化的发展、经济增速的放缓和房地产价格的变化，对于房地产投资的比重应谨慎。在低利率环境下，考虑到保险资金的长期性和利差等特征，保险资金需要积极创新，增加在基础设施方面的投资，同时不断提升资产管理能力。

随着我国保险业的快速发展，部分保险公司相对缺乏有效的风险管理策略，从而对未来保险业健康良好的发展起到了一定的限制作用。本文通过度量保险业整合风险，为保险公司提供风险度量的工具，为其进行合理的资产配置提出了建议。随着保险业的不断发展，风险管理意识不断加强，Copula-CVaR模型也将愈发成熟，风险管理的手段也会愈发完善。

本文存在的不足之处：首先，本文未研究高维Copula函数的pair-Copula以及藤Copula估计方法，若能运用多种方法进行估计，结论的可靠性将增大；其次，本文未考虑保险资金海外投资这一重要因素；再次，研究样本获取期间为2011-2013年，如果能延长样本区间，则研究成果代表性更强。

[参考文献]

[1] 马建堂， 董小君， 时红秀等. 中国杠杆率与系统性金融风险防范[J]. 财贸经济， 2016， (1)： 5-21.

[2] 卞世博, 刘海龙. 市场风险与违约风险同时存在下的最优资产配置[J]. 管理工程学报, 2013, (1): 160-165.

[3] 田玲, 王正文, 许潆方. 基于经济资本的我国保险公司投资风险限额配置研究[J]. 保险研究, 2011, (11): 31-38.

[4] Sklar, A.. Functions de Repartition an Dimension et Luers Marges[J].PublicationsdeInstititutdeStatistiqueUniversiteDeParis, 1959, (8): 229-2231.

[5] Klugman, S. A., Parsa, R.. Fitting Bivariate Loss Distributions with Copulas[J].Insurance:MathematicsandEconomics, 1999, 24(1): 139-148.

[6] Embrechts, P., Mcneil, A., Straumann, D.. Correlation: Pitfalls and Alternatives[J].Risk, 1999, 12(5): 69-71.

[7] McNeil, A. J., Frey, R.. Estimation of Tail-related Risk Measures for Heteroscedastic Financial Time Series: An Extreme Value Approach[J].JournalofEmpiricalFinance, 2007, 7(3): 271-300.

[8] Romano, C., Clemente, A. D.. Measuring Portfolio Value-at-Risk by a Copula-EVT Based Approach[R]. University of Rome “La Sapienza”, 2003.

[9] Rosenberg, J., Schuermann, T. A.. General Approach to Integrated Risk Management with Skewed, Fat-tailed Risks[R]. Working Paper of Federal Reserve Bank of New York, 2004.

[10] Eric Jondeau, Michael Rockinger. The Copula-GARCH Model of Conditional Dependencies: An International Stock Market Application[J].JournalofInternationalMoneyandFinance, 2006, 25(5): 827-853.

[11] 白保中，宋逢明，朱世武. Copula函数度量我国商业银行资产组合信用风险的实证研究[J]. 金融研究, 2009, (4): 129-142.

[12] Fengge, Y., Hongmei, W., Jiaqi, L.. CVaR Measurement and Operational Risk Management in Commercial Banks Based on Peak Value Method of Extreme Value Theory[J].MathematicalandComputerModelling, 2013, 58(12): 15-27.

[13] Ward, L. S., Lee, D. H.. Practical Application of the Risk-adjusted Return on Capital Framework[R]. Dynamic Financial Analysis Discussion Papers, CAS Forum Summer, 2002.

[14] 梁冯珍, 史道济. 基于Copula函数的保险准备金的确定方法[J]. 统计与决策, 2006, (24): 142-144.

[15] 陈辉, 陈建成. 我国保险投资组合的模拟和金融风险测量研究[J]. 统计研究, 2008, (11): 64-71.

[16] Artzner, P., Delbaen, F., Eber, J. M., et al.. Coherent Measures of Risk[J].MathematicalFinance, 1999, 9(3): 203-228.

[DOI]10.14007/j.cnki.cjpl.2016.02.007

[引用方式]王大鹏, 赵正堂. 中国保险业资产配置与风险整合——基于虚实配比、 Copula-CVaR模型和Monte Carlo算法的实证研究[J]. 产经评论, 2016, 7(2): 71-82.

[责任编辑：陈林]

Research on Risks Integration and Asset Allocation in Chinese Insurance Industry——Based on Virtual Reality Matching, Copula-CVaR and Monte Carlo Algorithm

WANG Da-pengZHAO Zheng-tang

Abstract:Chinese leverage ratio is lower than developed countries, but it has been on the rise. The risk from capital market, bank sector, even the currency market can transmit to the real economy. Though building Copula-CVaR model, we researched the integration risk in insurance industry. We researched the relevance of four assets yield rates. The Copula-CVaR model connects the yield rate distribution function with Monte Carlo simulating. By computing the CVaR of insurance industry we measured the value of the integration risks of the whole industry and found the best asset weight under the best CVaR. The empirical results show that increasing the proportion of bonds and stocks(funds) will increase the value of integration risks. We should invest more money to infrastructure, and pay more attention to real estate risk coved by the rising house price.

Key words:insurance industry; virtual reality matching; asset allocation; integration risks; copula-CVaR Model

[中图分类号]F842

[文献标识码]A

[文章编号]1674-8298(2016)02-0071-12

[作者简介]王大鹏，北京大学光华管理学院博士后，研究方向：保险资产管理、风险管理；赵正堂，厦门大学经济学院副教授，研究方向：保险经济学、保险精算。

[收稿日期]2015-12-14