波形钢腹板箱梁剪力滞效应研究

冯天鹏，徐向锋，张 峰，姜瑞娟

(1. 宁夏公路建设管理局，宁夏 银川 750000；2. 山东交通学院，山东 济南 250061；3. 山东大学 岩土与结构工程研究中心，山东 济南 250061)

波形钢腹板箱梁剪力滞效应研究

冯天鹏1，徐向锋2，张 峰3，姜瑞娟3

(1. 宁夏公路建设管理局，宁夏 银川 750000；2. 山东交通学院，山东 济南 250061；3. 山东大学 岩土与结构工程研究中心，山东 济南 250061)

为了研究波形钢腹板箱梁的剪力滞效应，建立了考虑波形钢腹板剪切变形的箱梁纵向位移翘曲函数，考虑顶底板的纵向、面内剪切变形能和钢腹板的剪切变形能；基于能量变分原理，推导了适用于波形钢腹板箱梁剪力滞分析的解析解；综合对比模型试验、有限元分析及变分解析解的计算结果。研究表明：推导的波形钢腹板剪力滞解析解计算结果与模型试验、有限元分析结果吻合；集中荷载加载工况下，剪力滞影响区域仅在加载位置左右两侧附近很小范围；加载位置越靠近支座位置，剪力滞效应越明显；宽高比对剪力滞无影响，剪力滞系数与宽跨比呈线性相关；翼缘板宽度增加后箱梁的剪力滞系数增大。

桥梁工程；波形钢腹板；箱梁；剪力滞；变分；模型试验；有限元

0 引 言

波形钢腹板组合箱梁桥[1]是一种以波形钢板取代混凝土腹板的钢-混组合结构桥梁形式(图1)，具有自重轻、力学效能优越、便于装配施工、造价低、耐久性好和全寿命期经济效益高、低碳节能等众多优点。与混凝土箱梁桥、钢箱梁桥、传统的平钢腹板组合箱梁桥一样，波形钢腹板组合箱梁桥在荷载作用下翼缘板会有剪力滞效应，在该类桥梁的设计中是否考虑剪力滞效应关乎桥梁的纵向抗弯承载力乃至桥梁的整体安全性。

图1 波形钢腹板箱梁Fig.1 Corrugated steel web box girder

奥地利、英国、澳大利亚与前联邦德国在1969年11月到1971年11月期间相继发生了4起钢箱梁失效或破坏事故，经分析发现4座桥梁设计时忽略剪力滞效应是事故发生的重要原因。国内学者针对波形钢腹板组合箱梁桥剪力滞效应做了一些研究。吴文清[2]最早采用理论分析、数值模拟和模型试验的技术手段，对等截面波形钢腹板组合箱梁桥的剪力滞问题进行研究。翼伟等[3]基于三次抛物线的位移假定用变分法求解等截面简支梁的剪力滞效应。周茂定等[4]用比拟杆法分析简支波形钢腹板组合箱梁剪力滞效应。喻文兵[5]通过足尺量试验研究了简支波形钢腹板组合箱梁桥的剪力滞效应。马磊等[6]在某三跨单箱三室波形钢腹板箱梁上进行了测试并计算了翼缘有效宽度计算系数，指出现有的国内外桥梁规范均无法准确给出单箱三室波形钢腹板箱梁翼缘有效宽度计算系数。 朱越峰等[7]认为与普通混凝土腹板箱梁相比，波形钢腹板组合箱梁由于腹板纵向刚度小，剪力滞效应不明显。变截面波形钢腹板组合箱梁剪力滞效应在近期也有一些初步的研究成果。周勇超等[8]在所推导等截面波形钢腹板剪力滞效应的微分方程上，将截面刚度系数由常数变为关于桥长方向的函数，得到变截面波形钢腹板剪力滞效应的微分方程。

综合来看，波形钢腹板组合箱梁桥剪力滞效应研究成果还较少。由于能量变分方法可以获得闭合解，可以定性分析各种参数对剪力滞的影响情况，在普通PC箱梁上已有不少研究。为此，进一步开展基于能量变分方法在波形钢腹板箱梁上的应用具有理论价值和工程意义。

1 基本假定及控制微分方程

1.1 基本假定

波形钢腹板单箱单室箱形梁截面参数以及坐标如图2，坐标原点取在截面的形心。

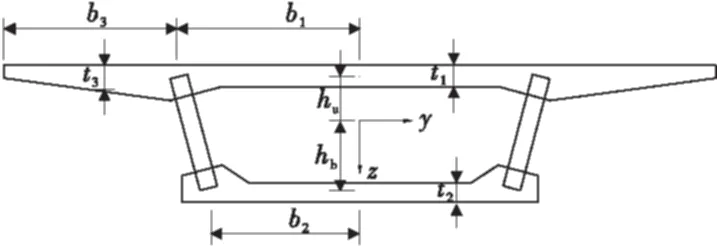
图2 波形钢腹板箱梁截面构造 Fig.2 Cross-section structure of corrugated steel web box girder

根据波形钢腹板箱梁的受力特点，公式推导中采用以下假定[1]：

1)忽略钢腹板的抗弯性能，仅仅考虑其竖向抗剪性能；

2)波形钢腹板箱梁的顶、底板及翼缘板符合“拟平截面假定”；

3)忽略顶、底板及翼缘板的横向应变(εy=0)及竖向应变(εz=0)，忽略顶、底板及翼缘板的面外剪切应变(γzy=γxz=0)。

1.2 控制微分方程

定义图1所示的薄壁箱梁的梁体竖向变形为w，纵向变形为u。外荷载作用下波形钢腹板箱梁产生剪切变形γxz[9]，因此经典Euler梁理论不再适用，需要依据Timoshenko梁理论开展计算分析。箱梁中性轴的转角φ可表示为

φ=w′-γxz

(1)

波形钢腹板的竖向剪切变形由式(2)确定：

(2)

式中：Q为剪力；Ge为波形钢腹板有效剪切模量；Aw为波形钢腹板横截面面积。

波形钢腹板纵断面尺寸如图3。

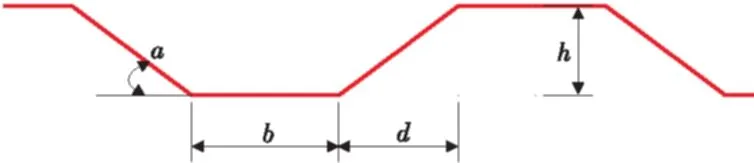
图3 波形钢腹板纵断面Fig.3 Profile of corrugated steel web

波形钢腹板有效剪切模量Ge为

Ge=G(b+d)/[b+dsec(α)]

(3)

式中：b，d，α的意义参见图3；G为钢材的剪切弹性模量。

定义顶、底板及翼缘板翘曲位移差为U，则顶、底板及翼缘板的翘曲位移描述为

(4)

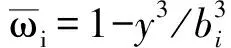
波形钢腹板箱梁的总势能泛函由顶板、底板及腹板的变形能和外荷载势能叠加组成。

1.2.1 应 变

由式(1)知波形钢腹板竖向剪切应变γxz：

γxz=w′-φ

(5)

基于式(4)，顶、底板及翼缘板的正应变εi为

(6)

顶、底板及翼缘板的面内剪应变γi为

(7)

1.2.2 变形能

波形钢腹板的变形能Vw描述为

(8)

式中：l为梁长；hw为波形钢腹板竖向高度；tw为波形钢腹板厚度。

顶、底板及翼缘板的变形能描述为

(9)

式中：E为混凝土弹性模量；G为混凝土剪切模量；t1，t2及t3参见图2。

1.2.3 外荷载势能

横向荷载作用下的梁段参见图4。

图4 梁段荷载Fig.4 Beam load

由图4可见，外荷载势能W由横向荷载及梁段端部剪力和弯矩共同作用：

(10)

式中：M为梁段弯矩；q为横向荷载；Q为梁段剪力。

考虑梁体平衡，有Q=dM/dx,q=-dQ/dx，代入式(10)，通过分部积分式(10)可变形为

(11)

式中：第1项为弯曲势能；第2项为剪力势能。

1.2.4 微分方程

体系总势能Π：

Π=Vw+V1+V2+V3-W

(12)

通过推导可得到体系总势能的表达式为

(13)

需要注意的是式(8)和式(12)的第2项值相等，在推导过程中刚好抵消。

对箱形梁总势能泛函求一阶变分，根据变分原理δΠ=0，得箱梁受力变形的微分方程:

(14)

(15)

边界条件:

(16)

求解得到纵向翘曲位移差函数U后，即可根据式(14)求解得到φ′，代入式(6)求解顶、底及翼缘板的纵向正应变，进而求解得到波形钢腹板箱梁的剪力滞系数。

2 波形钢腹板简支箱梁的剪力滞效应

图5为简支梁在集中荷载作用下加载示意。

图5 简支梁加载示意Fig.5 Loading sketch of simply supported beam

当集中荷载P作用于简支箱梁的跨内任意位置处时，内力和位移等均需要分段表达。在P作用点以左梁段，物理量加载下标“1”，在P作用点以右梁段，物理量加载下标“2”。a，b为加载点距离支座的距离。

当0≤x≤a时，梁体剪力Q=b/lP。由式(15)可得

(17)

式中：C1和C2为待定系数。

当a

(18)

式中：C3和C4为待定系数。

(19)

由边界条件求得待定系数：C1=0,C2= sh[k(l-a)]/[k2sh(kl)]，C3=sh(ka)/k2，C4=-sh(kb)/[k2th(kl)]。

求得剪力滞系数：

(20)

(21)

式中：B=sh(ka)ch(kx)-sh(ka)cth(kl)sh(kx)。

3 波形钢腹板箱梁剪力滞系数

3.1 波形钢腹板简支箱梁模型试验

波形钢腹板采用优质低碳钢，厚度为1 mm，细部参数参见图3，其数值为b=20 mm，d=16 mm，h=12 mm。混凝土采用C30，其测定参数为：弹性模量E=30 000 MPa、极限压应变εcu=0.003 42 和泊松比μ=0.192。模型梁的尺寸参见图6，实际加载见图7。

图6 截面构造Fig.6 Cross-section structure

图7 跨中集中荷载加载Fig.7 Concentrated load loading of span center

3.2 模型试验与理论分析

基于ABAQUS软件建立模型试验梁，模拟了波形钢腹板内嵌入顶板和底板及横隔板的构造，共划分节点总数67 184，单元总数50 832，其中39 744个六面体单元(C3D8R)，11 088个壳单元(S4R)。具体有限元模型见图8，集中荷载加载下箱梁顶、底板纵向应力计算结果参见图9。

图8 有限元模型Fig.8 Finite element model

图9 箱梁顶、底板纵向应力(单位:Pa)

由图9可见，在集中荷载作用下，箱梁顶板及底板跨中位置均出现明显的剪力滞效应。

采用有限元数值模拟，笔者推导的解析解分别计算跨中加载25 kN时的顶板剪力滞效应，并与试验测试结果进行对比，具体结果参见图10。

图10 剪力滞对比Fig.10 Shear lag contrast

由图10可见：①有限元计算结果取顶板中面位置节点应力进行分析，由于在加载点位置有局部应力效应，最大剪力滞系数位置在横向稍有偏差；②笔者推导的公式所得结果与有限元和试验测试结果接近；③从试验测试结果和有限元分析结果可以看出，顶板的剪力滞效应要稍大于底板，为此后续分析中仅提取顶板剪力滞系数进行分析。

3.3 波形钢腹板箱梁的剪力滞影响参数分析

分析不同加载位置对箱梁纵向剪力滞的影响，剪力滞系数选取顶板与腹板交界位置的λe，具体参见图11。

图11 不同加载位置对剪力滞系数的影响Fig.11 Influence of different loading positions on shear lag coefficients

由图11可见：①集中荷载加载工况下，剪力滞效应仅在加载位置左右两侧附近很小区段内才有，该结论与图9的应力云图显示结果类似；②加载位置越靠近支座位置，加载位置处的剪力滞效应越明显，加载位置为0.17l时，剪力滞数值为2.140 8；加载位置为0.5l时，剪力滞系数为1.298 6，降低了40%。

吴文清[2]研究表明：波形钢腹板的钢腹板细部构造对剪力滞效应影响很少，可不考虑。进一步开展宽跨比(w/l)和宽高比(w/h)对λe的影响。需要注意的是，此时分析时，箱梁的宽度变化时，顶板和翼缘板的宽度做等系数变换，加载工况为跨中加载，剪力滞系数提取位置为跨中位置。计算结果见图12。

图12 箱梁尺寸对剪力滞系数的影响Fig.12 Influence of box girder size on shear lag coefficients

由图12可见：①宽高比(w/h)对剪力滞影响很小，分析其原因为箱梁纵向翘曲函数的定义与箱梁截面横向尺寸密切相关，与高度相关的仅有波形钢腹板的抗剪效应，而需要注意的是，式(8)和式(12)的第2项值相等，在推导过程中刚好抵消，导致体系总势能项与高度相关性很小；②宽跨比(w/l)对剪力滞影响较大，变分法的分析结果显示，剪力滞系数与宽跨比呈线性相关。

进一步分析箱梁的翼缘板宽度与顶板宽度比值(b3/b1)对剪力滞特性的影响。保持顶板宽度不变，仅变化翼缘板宽度，加载工况为：在跨中位置加载，剪力滞系数提取位置为跨中位置。具体分析结果见图13。

图13 b3/b1对剪力滞系数的影响Fig.13 Influence of b3/b1 on shear lag coefficients

由图13可见，b3/b1从0.17变化至1.65时，剪力滞系数从1.247 1变化至1.330 6，增加了6.7%。

4 结 论

1)建立了波形钢腹板箱梁纵向位移翘曲函数，考虑顶底板的纵向、面内剪切变形能和钢腹板的剪切变形能，基于能量变分原理推导了适用于波形钢腹板箱梁剪力滞分析的解析解。

2)集中荷载加载工况下，剪力滞效应仅在加载位置左右两侧附近很小区段内才有。加载位置越靠近支座位置，加载位置处的剪力滞效应越明显。

3)宽高比(w/h)对剪力滞影响很小，宽跨比(w/l)对剪力滞影响较大，剪力滞系数与宽跨比呈线性相关。

4)翼缘板宽度增加后箱梁的剪力滞系数增大。

[1] 刘玉擎. 组合结构桥梁[M]. 北京: 人民交通出版社, 2005. LIU Yuqing.CompositeStructureBridge[M]. Beijing: China Communications Press,2005.

[2] 吴文清. 波形钢腹板组合箱梁剪力滞效应问题研究[D].南京： 东南大学, 2002. WU Wenqing.ResearchonShear-lagEffectinCombinedBox-girderwithCorrugatedSteelWebs[D]. Nanjing: Southeast University,2002.

[3] 冀伟, 蔺鹏臻, 刘世忠, 等. 波形钢腹板箱梁剪力滞效应的变分法求解[J]. 兰州交通大学学报,2010,29(6):16-19. JI Wei, LIN Pengzhen, LIU Shizhong, et al. Variational principle of shear lag effect of composite box girders with corrugated steel webs[J].JournalofLanzhouJiaotongUniversity,2010,29(6):16-19.

[4] 周茂定, 刘世忠, 扬子江. 波形钢腹板组合箱梁剪力滞效应的比拟杆法求解[J]. 兰州交通大学学报,2012,31(4):41-44. ZHOU Maoding, LIU Shizhong, YANG Zijiang. Bar simulation method on shear lag effect of composite box girder with corrugated steel web[J].JournalofLanzhouJiaotongUniversity,2012,31(4):41-44.

[5] 喻文兵. 波形钢腹板PC组合箱梁足尺梁静载试验研究[D]. 南京: 东南大学, 2005. YU Wenbing.FullScaleGirderStaticLoadStudyonCombinationBoxGirderofCorrugatedSteelWebPC[D]. Nanjing: Southeast University,2005.

[6] 马磊, 周林云, 万水. 单箱三室波形钢腹板箱梁剪力滞效应研究[J]. 中外公路,2013,33(3):95-99.

MA Lei, ZHOU Linyun, WAN Shui. Shear lag sudy of single box three rooms corrugated steel box girder[J].JournalofChina&ForeignHighway,2013,33(3):95-99.

[7] 朱越峰, 吴朴, 谢旭, 等. 部分波形钢腹板箱梁桥受力特性分析[J]. 浙江大学学报(工学版) ,2008,42(1):122-128. ZHU Yuefeng, WU Pu, XIE Xu, et al. Mechanical behavior of box girder bridge with partial corrugated steel webs[J].JournalofZhejiangUniversity(EngineeringScience),2008,42(1):122-128.

[8] 周勇超, 郝宪武, 李子青. 变截面波形钢腹板组合梁剪力滞效应[J]. 长安大学学报(自然科学版),2014,34(4):249-250. ZHOU Yongchao, HAO Xianwu, LI Ziqing. Shear lag effect of non-uniform composite beam with corrugated steel web[J].JournalofChang’anUniversity(NaturalScienceEdition),2014,34(4):249-250.

[9] 李宏江, 叶见曙, 万水, 等. 剪切变形对波形钢腹板箱梁挠度的影响[J]. 交通运输工程学报,2002,2(4):17-20. LI Hongjiang, YE Jianshu, WAN Shui, et al. Influence of shear deformation on deflection of box girder with corrugated steel webs[J].JournalofTrafficandTransportationEngineering,2002,2(4):17-20.

Shear Lag Effect of Box Girder with Corrugated Steel Webs

FENG Tianpeng1, XU Xiangfeng2, ZHANG Feng3, JIANG Ruijuan3

(1. Ningxia Highway Construction Administration Bureau， Yinchuan 750000, Ningxia, P. R. China; 2. Shandong Jiaotong University, Ji’nan 250061, Shandong, P. R. China;3. Geotechnical and Structural Engineering Research Center, Shandong University, Ji’nan 250061, Shandong, P. R. China)

In order to study the shear lag effect of box girder with corrugated steel web plate, the longitudinal displacement warping function of box girder was established, which considered the shear deformation of corrugated steel web plate, longitudinal and in-plane shear deformation of the top and the bottom flange. Based on the energy variational principle, an analytical solution was derived for the shear lag analysis of the box girder with corrugated steel webs. Results of model test, finite element analysis and variational solution method were compared with each other. Study shows that: the calculation results of the shear lag effect of box girder with corrugated steel webs are in a good agreement with those of the model test and finite element analysis; the effect area of shear lag only occurs at both sides near the loading position in a very small range; the closer the loading position near the bearing position, the more obvious the shear lag effect. The ratio of width to height has no effect on shear lag. The shear lag coefficient is linearly related with the ratio of width to span. The shear lag coefficient of box girder increases with flange width.

bridge engineering; corrugated steel webs; box girder; shear lag; variation; model test; the finite element

2015-07-29；

2015-12-20

宁夏交通厅科技项目(201504)；国家自然科学基金项目(51578323)

冯天鹏(1972—)，男，宁夏人，高级工程师，主要从事交通建设方面的研究。E-mail：841177536@qq.com。

10.3969/j.issn.1674-0696.2016.06.03

U448. 213

A

1674-0696(2016)06-011-05