城市分形中心与占优标度区选择

黄伟力

(江西科技学院 信息工程学院，南昌 330098)

城市分形中心与占优标度区选择

黄伟力

(江西科技学院 信息工程学院，南昌 330098)

用回转半径法研究城市分形特征时，中心点位置的选择至关重要。以反映城市基础设施情况的兴趣点(point of interest，POI)作为基础数据，分析中心点位置对标度区识别的影响。将POI几何中心、重心、密度中心、中心城区几何中心和重心5种统计中心作为待选中心，给出辐射范围、核心密度与分形维数、中心漂移度等标度区相关指标，提出判断占优标度区的POI数量最大化原则。通过统计中心与地标中心标度区对比，确定城市分形中心和占优标度区。省会城市及直辖市标度区分析结果显示：统计中心各有优劣，占优中心总体上更倾向于POI几何中心和密度中心，地标中心有时优于统计中心；密度中心对应的占优标度区半径维数较低，若半径维数太低则容易陷入局部密度中心；中心漂移度指标表明可能存在更好的分形中心选择方案。

占优标度区；分形中心；回转半径法；兴趣点；半径维数

0 引言

B.B.Mandelbrot用英国海岸线的自相似(self-similar)现象揭示了自然界的普遍规律[1]，从此分形(fractal)成为了各个学科领域的研究热点，越来越多的研究表明分形无处不在。城市地理学中的分形具有深刻内涵，它不仅是数学上的完美表达，而且还有重要的现实意义。城市分形研究主要集中在城市边界[2-4]、土地利用[5-10]、人口分布[11-15]、城市结构[16-21]等方面。分形维数(分维)是城市分形研究的重要指标，计算城市分维的常见方法有网格计数法和回转半径法。网格计数法用不同尺度的标尺量测空间，依据测量尺度与测量空间的标尺数量可以计算出城市形态的边界维数、容量维数和信息维数。回转半径法以某个中心点为圆心将城市划分为若干同心圆环，依据圆形区域内城市要素(如土地面积、人口数量等)与半径的关系，可计算出半径维数并得到一个圆形标度区(scaling region，也称为无特征尺度区或无尺度区)。回转半径法得到的标度区是一个统计意义上的分形区域，该标度区的中心(圆心)可以认为是分形中心，半径维数的大小则表征了该区域的向心聚集程度。半径维数越小，则标度区向心聚集程度越强，分形中心的聚集效应越明显；反之，该区域的空间布局越偏向于外围，距离分形中心越远。

城市图像的重心、政治中心、地标中心或某一城市职能用地的重心都是可选的分形中心。R.White等不考虑因城市生长所引起的中心偏移，尝试将城市原始中心(original centre)作为圆心[8]；F.Wang等根据人口密度衰减进行拟合，从6个可能的中心里选取拟合优度最高的东华门作为北京的中心[11]；姜世国等在研究北京城市形态的分形集聚特征时考虑到明清以来天安门是皇城的正门，是政治活动的中心，因此以北京天安门为中心点[5]；冯健研究杭州市人口密度空间分布时，考虑到武林广场是城市活动中心和市区几何中心，附近街道人口密度等级高且较稳定，所以将它作为杭州城市的中心[12]；刘妙龙等测算上海市人口分形时，城市中心选取上海市城市坐标系原点(国际饭店)，相应各区县中心选取它们的几何中心[13]；高向东等则是选取人民广场街道作为上海区域中心[15]；王铮等还研究了上海市商业重心对商业中心(CBD)的偏离，并发现商业重心移动滞后人口重心移动2年[22]。

圆心选取位置不同，所得到的标度区会出现显著差别。除了城市重心、政治中心、地标中心之外还有什么可供选择的方案？如何确定哪个标度区更为符合城市分形的特征，反映出城市集聚效应？ 圆心位置对标度区有什么影响？本研究就这些问题展开讨论，以GIS系统中的兴趣点(POI)信息为基础数据，从统计的角度提出几种分形中心的可选方案，并给出分形中心和占优标度区的判别方法，通过全国省会城市及直辖市的实例分析，对选择不同中心所得到的标度区做出比较，分析圆心点的选择对计算标度区的影响，讨论各种中心的筛选依据和适用场合。

1 数据来源与研究方法

1.1 数据

随着城市不断演化发展，城市中心的住宅用地逐渐被商业用地所替代，人口逐渐向外迁移。B.E.Newling发现人口密度将形成“火山口”和“波浪式推进”的演化特征，人口密度将在中心点形成一个相对低谷，其峰值会像波浪一样逐渐向外推移[23]。POI数据则不受这方面的影响，无论城市中心位置是住宅用地还是商业用地，其POI密度总是保持较高的水平。因此，与基于城市用地和人口数据的研究相比较，基于POI数据研究城市分形特征具有独特优势。本研究使用2012年MapInfo全国电子地图数据作为数据源，从政府机构、公园、大厦、宾馆酒店、医疗、学校、银行、药店、餐饮、公交站、出入口、收费站、停车场、超市商城、其他等图层提取了大约520万个POI数据，这些大规模数据信息内容丰富，覆盖面广，具有良好的城市形态表征能力。

1.2 统计中心

城市的功能分布可以看成是由若干个中心吸引点共同作用形成的。这些吸引点可以是政治中心，也可以是商业中心，还可以是各个行业中心等。除了这些有形的吸引点，也可能存在一些潜在的无形吸引点，例如几何中心、重心、密度中心等。每个吸引点的吸引强度以及辐射范围不同。有形的吸引点往往是根据历史经验得到的一些具体的众所周知的地标位置，而无形的吸引点则是通过综合计算推算出的统计中心点。

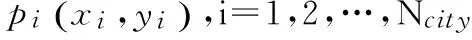
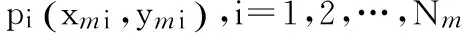
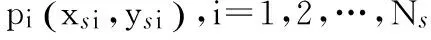
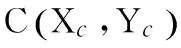
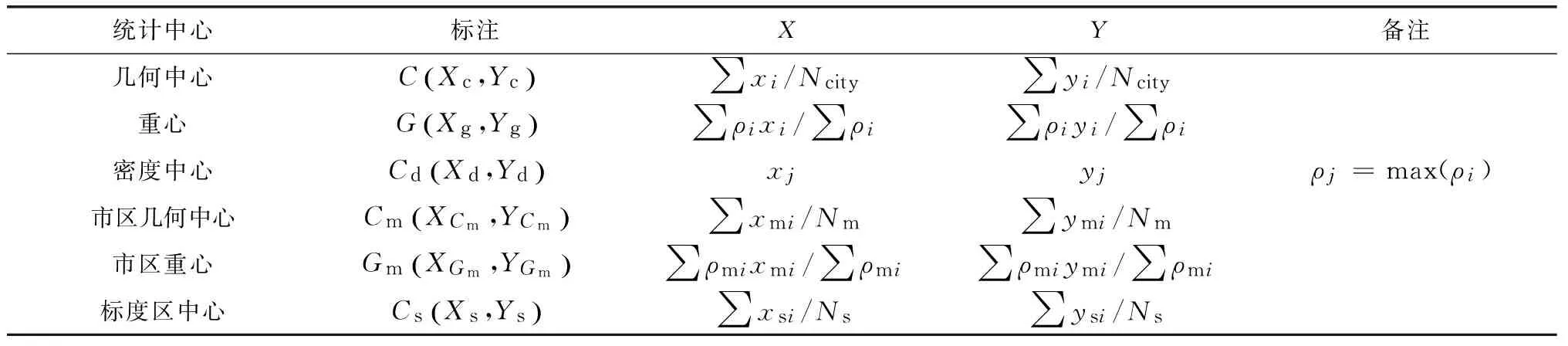
表1 统计中心点标记及位置Tab.1 The note and location of statistical centers

城市的发展受到集聚力和分散力的共同作用，一方面由于中心吸引产生强烈集聚效应，另一方面由于中心竞争日益激烈而向外不断扩张。POI则是城市集聚和扩张过程的有力见证者。POI密度反映了区域集聚程度，密度中心具有最强大的局部吸引力，往往是城市最繁华的地带，一些典型地标建筑就在附近。同时，POI随着城市的发展不断向外生长，与城市扩张保持了良好的一致性。由于受到了城市边界的限制，城市边界几何中心成为了城市均质扩张的中心点。对称性较好且发展均衡的城市，各类中心点的位置都会很接近；而实际上大部分城市对称性差且发展不均衡，密度中心和城市边界几何中心距离较远，在集聚力和分散力的合力作用下，POI几何中心C将落在密度中心和城市几何中心之间。

1.3 分形测算及相关指标

幂律分布是分形的表现形式之一，使用回转半径法计算圆形区域内的POI数量N(r)与半径r之间的关系，若其符合幂率分布则N(r)可以表示为：

(1)

幂指数关系可以认为是对数线性关系，若双对数坐标下N(r)与r在一定区域呈现出线性关系，则可以判定分形的存在，这个区域就称之为标度区(scalingregion)。除了从直观上考察直线的拟合趋势之外，L.Benguigui等用拟合优度R2≥0.996和标准误差δ≤0.04作为判断城市是否分形的依据[24]。为了提高标度区识别的客观性与准确性，王成栋等采用基于lnr-lnN(r)曲线二阶导数信息的自动识别方法[25]。本研究主要采用L.Benguigui提出的R2≥0.996标准来判断分形，对特殊情况适当做出微调。

1.3.1 标度区相关指标。为了判断标度区的优劣，将对标度区辐射范围、核心密度和半径维数、中心漂移度等方面做出比较，从而得到占优中心和占优标度区。

① 标度区的辐射范围。Rs和Ns是标度区最基本的指标，Rs表示标度区的辐射半径，Ns表示辐射区域内覆盖的POI数量。Rs和Ns一般表现出正相关性，即Rs越大则Ns越大。若中心点的选取不合理也可能出现较大的Rs对应较小的Ns，反映出标度区的整体吸引力较弱，该标度区的中心点大多不是真正的城市中心，而是局部中心。

② 核心密度与半径维数。k和D是N(r)所服从幂率分布中的重要参数，k可以理解为分形中心密度(即核心密度)，D则表示POI的半径维数。k值越大则中心集聚密度越大，说明中心引力越强。D取值一般为1～2之间，表明标度区密度随半径增加而逐渐递减；若D越接近2，则表明标度区密度保持稳定，与中心密度相同。当D>2时，标度区密度随半径增加而逐渐增大，这是一种不正常现象，一般只在中心密度很低的情况下出现。若所选取的中心为局部中心，则可能出现D<1的现象，标度区密度随半径增加而迅速递减，此时标度区所覆盖的POI数量较小。

(2)

若所选中心点是城市分形中心，该中心点附近的POI应该向其聚集，且体现出对称性，这样以该中心点计算的标度区中心应该与其基本重合，即距离很小。φ值在0～1之间，φ值越小表明所选取中心点与标度区几何中心越靠近，φ值越大则表明以所选中心点计算的标度区中心有明显的偏移，可能存在更好的中心点。

④ 占优标度区和占优中心。根据标度区的相关指标，可以判断出同一城市不同标度区划分的优劣关系。若标度区S1优于标度区S2，则称S1为占优标度区；S1对应的中心圆点成为占优中心。

由于判断标度区优劣的指标较多，不同指标的判断结果可能表现出不一致性，标度区选择问题成为了一个多目标问题。为了简化处理过程，根据指标的重要程度来排序，将这些指标分为第一指标、第二指标等，以此解决指标之间的冲突。例如，可以将Rs作为第一指标，Ns作为第二指标，这就是Rs最大化原则；还可以将Ns作为第一指标，Rs作为第二指标，这就是Ns最大化原则。

对多个城市的实验中发现使用Rs最大化原则计算容易出现较大偏离，可能得到某个区县中心的标度区，Rs虽然最大，Ns却随着Rs迅速减少。本研究采用的判断方法为Ns最大化原则，标度区辐射区域内所覆盖的POI数量越多，则该区域的聚集程度越好，说明其中心引力越强。使用Ns最大化原则得到的标度区称为Ns占优标度区，与之对应的中心圆点称为Ns占优中心。

1.3.2 占优标度区与分形中心测算方法。由于核心区域与外围郊区发展速度不同，城市会出现双标度区，这是一种双分形(bifractal)结构[5,8,16]。双标度区的存在反映了城市核心吸引力和凝聚力，为中心城区范围的界定提供了依据。对不同中心点使用回转半径法，根据L.Benguigui标准和双标度区边界可以确定标度区。

① 计算候选中心点位置，得到C，G，Cd，Cm，Gm。

② 分别计算每个POI点到各中心的距离。

③ 以1km为半径公差，对不同中心点分别统计各环POI数量N(r)。

④ 用幂指数曲线拟合不同半径r下的POI数量N(r)，以0.996为拟合优度阀值，计算出第一标度区半径Rs、POI数量Ns，以及核心密度k、分形维数D。

⑤ 计算第一标度区中心点Cs，由此得出中心漂移度φ。

⑥ 按Ns最大化原则选择Ns占优标度区和Ns占优中心，并结合标度区的Rs,k,D,φ指标，综合分析标度区优劣，得到城市分形中心优选方案。

2 结果分析

2.1 北京市分形中心实验

2.1.1 分形中心对比。北京作为首都，城市建设和经济发展都较为成熟，研究其城市分形特征具有一定代表性。图1给出了以几何中心C为圆心使用回转半径法计算的POI数量与半径的双对数坐标图，在14 km内第一标度区保持了良好的线性趋势，拟合优度为 0.997 1；14 km之外的第二标度区分维系数(0.271 3)降低明显，拟合优度为0.869 3。第一标度区半径维数为 1.718 4，这也与M.Batty等借助受限扩散凝聚模型和电介质击穿模型得到的城市形态平均维数1.71相吻合[2]。

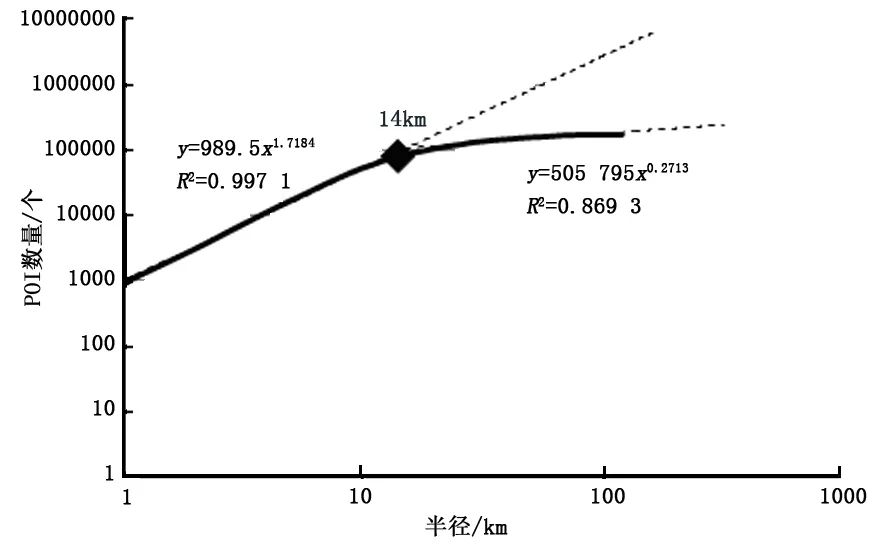
图1 北京市POI分形效果Fig.1 POI fractal in Beijing City

表2给出了北京市各中心点坐标以及相应标度区的指标。统计中心指标的拟合优度阀值均设置为 0.996，人工选取的地标中心拟合效果较弱，故将阀值设置为0.995。可以看出，以北京市POI几何中心C为圆心的标度区辐射范围最大(14km)，该区域内包含POI数量达80 322个，占北京POI总数的46.8%(总数为171 464)。核心密度在1km半径的圆形区域内约有989个点，分维系数为1.718 4。但是中心漂移度φ指标较大，说明标度区的中心有所偏离。

为了深入分析标度区的中心偏离，图2给出了北京各POI分形中心的具体位置及以C为中心的标度区范围。标度区中心点Cs与Gm的位置接近，标度区有明显的东北偏向趋势。这主要由于北京市发展存在不均衡性，东北部发展较快，资源、要素密集；西南区域由于产业结构、原有资源条件等因素的影响，经济发展相对缓慢。首都西南区域拥有北京市近1/3的土地和1/4的总人口，但2007年西南五区GDP总量和财政收入仅占北京市的1/8和1/16[26]。除此之外，北京的自然地理形态也是标度区向西北偏移的重要原因。天安门广场地处北京心脏地带，是最重要的地标中心，五环以内市区都具有强大吸引力，集聚效应明显。这种吸引属于显性吸引，天安门周边POI密度普遍高于其他区域，北京市的密度中心Cd就与天安门位置十分接近。另一方面，北京功能区域由首都功能核心区向城市功能拓展区、城市发展新区和生态涵养发展区不断扩展，遍布全市16个区县。假设北京城市功能的扩张是均质的，那么扩张后的中心则应该是北京城市的几何中心。不难计算，这个中心位于昌平区，接近昌平、顺义、怀柔三区交界之处，远在六环之外。然而，北京Ns占优中心既不是城市几何中心，也不是城市局部引力最强的密度中心，而是POI几何中心C，为什么它会具有特殊的吸引力呢？这是由于城市发展过程中集聚和扩张同时存在，POI几何中心在集聚力和分散力的合力作用下落在了位于密度中心和城市几何中心之间北三环附近，该点的吸引属于隐形吸引。标度区最终由五环内的高密度区和五环外的低密度区构成，具有明显偏态特征，Cs向高密度区所在方向偏移。POI重心G的计算考虑了POI密度的权重，市区几何中心Cm和市区重心Gm的计算则忽略了密云县和延庆县，这都使得它们的位置更接近密度中心。

表2 北京市各中心点标度区对比Tab.2 Comparison of scaling regions for different centers in Beijing City

说明：*天安门周边POI数量较少，故标度区从2 km处开始。

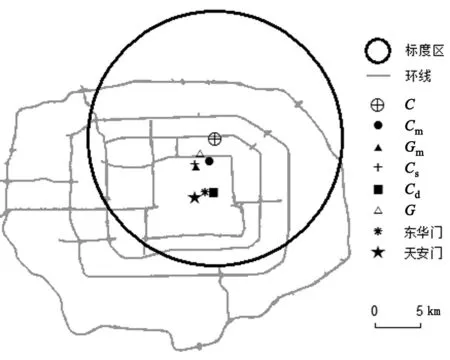
图2 北京市POI分形中心及标度区Fig.2 The center and scaling region of POI fractal in Beijing City

2.1.2 各区县分形中心实验。城市标度区判别方法同样可以应用于区县级别。将POI按照区县划分，在各个区县范围内设置中心点并计算标度区，通过Ns值最大原则可以确认占优标度区。图3给出了北京区县的POI标度区。东城区、西城区、海淀区、朝阳区、通州区、大兴区6个区域标度区半径较大，表明这些区域发展较快。

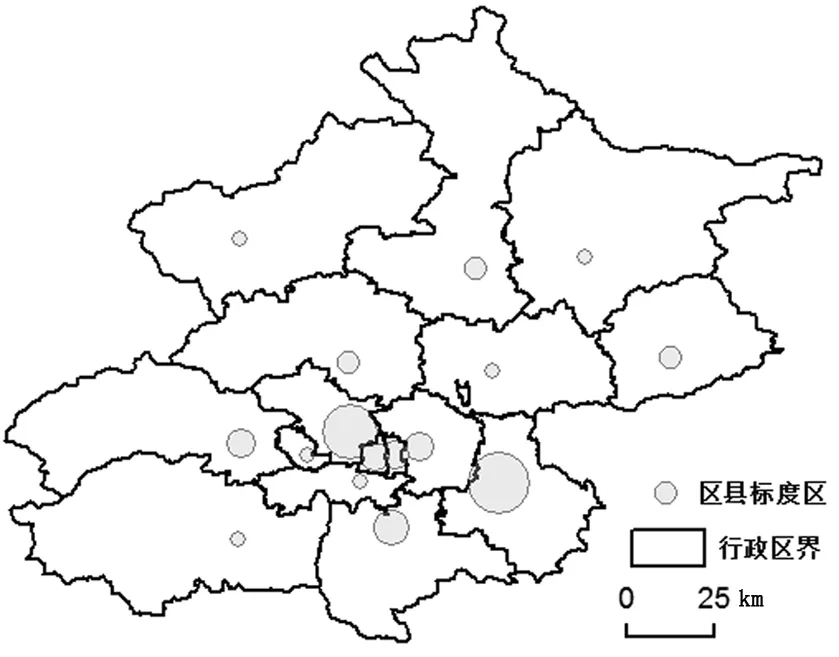
图 3 北京区县POI分形中心及标度区Fig.3 The centers and scaling regions of POI fractal in districts of Beijing

2.2 全国省会城市及直辖市分析

通过计算全国省会城市及直辖市各类统计中心点，分析相应的标度区，得到占优标度区(表3)，特点如下。

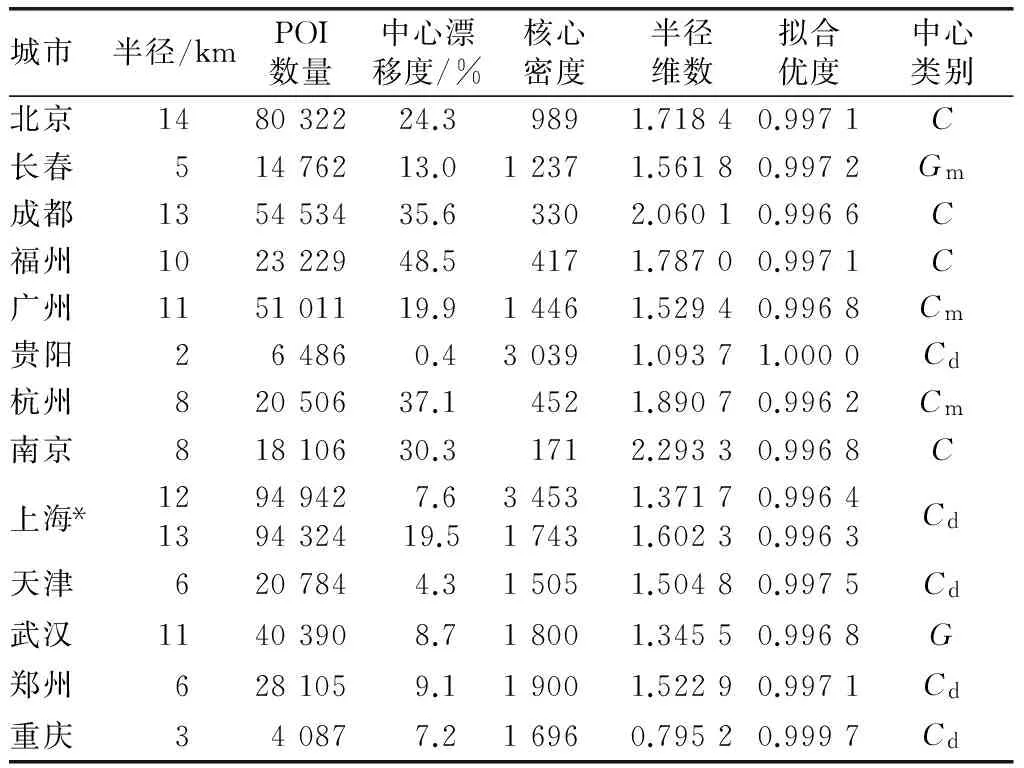
表3 全国部分省会城市及直辖市占优标度区指标Tab.3 The metrics of dominated scaling regions for major Chinese cities

说明：*表示上海的标度区按Rs和Ns的判断结果不一致。

① 由于各城市的地理条件和发展速度不同，各类型中心点对应的标度区都可成为占优标度区，其中POI几何中心C和密度中心Cd更为普遍，而重心G和市区重心Gm概率较低。市区几何中心Cm和市区重心Gm对某些地理形态对称性差的城市(如广州、长春)较为有效。

② 城市半径维数大部分都在1～2之间。成都、南京的半径维数大于2，表明从该中心到外围的生长过程中，POI密度越来越大，这主要是由于它们的核心密度都较低，半径维数最大的南京(2.293 3)核心密度仅有171，这表明只有核心密度小才有向外增长的空间。

③ 占优中心为密度中心Cd的占优标度区半径维数偏低，主要集中于1.2～1.3。天津和郑州D值较高，达到1.5；贵阳、重庆等城市则D值较低，预示该中心很可能是局部密集中心。尤其重庆作为直辖市，标度区半径仅为3km是很不正常的现象，在后面的讨论中将有更为详细的分析。

④ 通常按Ns最大化原则和按Rs最大化原则计算占优标度区的结果是一致的，但也有少数城市(如上海市)会出现不一致的情况。上海按密度中心Cd计算和按几何中心C计算Ns相差不大，显然Cd对应的12km标度区内平均POI密度更大(其φ指标也更好)，这时选择Cd作为分形中心会显得更加合理。

⑤φ指标表明分形中心与标度区几何中心Cs有一定的偏离。平均中心漂移度为19.3%，而福州高达48.5%。这意味着或存在更好的分形中心选择方案。

2.3 典型地标中心标度区分析

北京标度区分析中发现常用的地标中心(天安门、东华门)并不是占优中心，这是偶然还是普遍现象呢？接下来对杭州、上海、重庆3个城市各选取了2个地标中心进行实验，做进一步的分析(表4)。

表4 杭州、上海、重庆地标中心标度区Tab.4 Scaling regions for well-known centers in Hangzhou, Shanghai and Chongqing

说明：*解放碑标度区从2 km处开始。

2.3.1 地标中心和统计中心。以杭州市武林广场为中心得到的标度区半径Rs仅为5km，Ns为18 290。以上海市国际饭店为中心得到的标度区半径Rs也仅为5km，Ns为34 503。这些均劣于统计中心得到的占优标度区指标。而上海市以人民广场为圆心计算得到的Rs(12km)，不及表3中最佳的标度区半径(13km)，但是Ns(95 582)也超过最大标度区覆盖的POI数量(94 942)，漂移度值(5.2)也优于密度中心的漂移度(7.9)。这一切都表明以人民广场为中心计算出的标度区优于其他统计中心点。统计中心对应的标度区不一定是最优的，完全可能存在更好的占优中心。因此，地标中心和统计中心各有优劣，统计中心(尤其是几何中心和密度中心)具有一定的优势。

2.3.2Rs最优化 和Ns最优化。一个有趣的现象，以萧山区密度中心为圆心计算得到的标度区半径为12km，远远超过以市区几何中心Cm为圆心的占优标度区(半径为8km)，但是Ns仅为13 499，核心密度为1 512，分维系数仅为0.855 1。说明按区县中心为圆心，可能会得到半径更大的标度区，但该中心点引力较城市中心要弱很多，集聚效应随半径增加迅速衰减。此例再次证明，Ns最大化原则比Rs最大化原则更有意义。

2.3.3 占优中心和最优中心。统计中心分析中重庆市的占优标度区半径Rs为3km，这显然与直辖市的身份不符。使用朝天门和解放碑两个地标中心进行分析，得到标度区半径最大为11km。实验表明，统计占优中心得到的占优标度区在某些特定的情况下会与最优标度区有相当大的差别，这种现象在分维系数D<1时尤需注意。D<1的标度区对应的往往是城市密度中心，且不具有足够的吸引力，很可能是局部密度中心，而不是真正具有强大吸引力的城市分形中心。

2.4 城市分形中心的复杂性分析

城市是人类经济活动的中心，城市出现和发展及至当今城市时代的来临是人类社会复杂演化的结果[27]。城市功能结构和形态的聚集源自于吸引，城市中心、次中心以及局部热点的吸引产生了中心功能聚集区和区域功能聚集区。当某点存在强烈吸引力时，周边会产生一个集聚的自组织区域。由中心地体系和区位理论可知，距离中心越近的位置拥有更高的价值。因而，距离中心点越近，空间密度越大，同时竞争也越强烈。由于空间受到限制，当竞争压力大到某个程度时(即区域密度达到某个阀值)，内层空间的竞争力将逐渐减弱，自组织区域将向外层扩散。在这个演化过程中，中心区域的空隙将不断被填充，形成了聚集效应；中心密度达到一定程度之后，中心空间价值低于外围空间价值，于是出现了扩散现象。城市分形就是在不断的聚集和扩散中形成的。城市中心点的位置直接影响了城市演化生长的结构和形态，找到城市分形中心有着重要的理论价值和实践意义。

城市地理系统的演化是力图在混沌和有序之间寻求一种平衡[28]。因此，城市中心点位置的细微移动可能导致相应标度区的剧烈变化。1990年新经济地理学的主要代表人物克鲁格曼以对厂商之间向心力和离心力及其相互作用的分析为基础,清楚地阐明了由“一只看不见的手”作用在大范围内形成有规则经济空间格局的内在机理, 即“从不稳定产生秩序”的基本原理[29]。

地标中心属于城市的显性吸引点。城市在演化发展的过程中，由于受到政治、经济、地理等因素的影响，城市结构和形态会被扭曲或拉伸，中心点往往偏离显性吸引点。统计中心则是隐性吸引点，是依据城市现有结构和形态计算得到的。在“一只看不见的手”的作用下，统计中心可能与城市分形中心吻合得更好。除了这5种常见的统计中心，完全可能存在其他的计算方法，可以发现城市真正的分形中心。

3 结论与讨论

3.1 结论

1)各统计中心各有优劣，占优中心更倾向于兴趣点(POI)几何中心C和密度中心Cd，有时地标中心会是更好的选择。2)城市半径维数大部分都在1～2之间，部分核心密度很小的城市半径维数大于2。3)半径维数小于1的标度区更可能是局部密度中心。4)辐射区域内覆盖的兴趣点(POI)数量Ns最大化原则比标度区的辐射半径Rs最大化原则更为合理。5)中心漂移度φ指标表明可能存在更好的分形中心选择方案。对北京16个区县的实验表明，该方法同样可以找到区县的占优中心及标度区。

3.2 讨论

标度区优劣的判断指标是一个多目标的问题，Ns最大化原则比较单一，特殊情况下还需要人工选择，如果能设计出反映标度区优劣的综合指标则可大大简化判断过程。此外，下一阶段将进一步研究避免占优标度区陷入局部密度中心的方法，设计最优标度区和最优中心的定位方法以及多中心城市的占优标度区识别方法。

[1] Mandelbrot B B.How Long is the Coast of Britain[J].Science,1967,156(3775):636-638.

[2] Batty M,Longley P A.Fractal Cities:A Geometry of Form and Function[M].London:Academic Press,1994.

[3] Batty M.Cities and Complexity:Understanding Cities through Cellular Automata,Agent-based Models and Fractals[M].Cambridge,MA:The MIT Press,2007.

[4] Tannier C,Thomas I,Vuidel G,etal.A Fractal Approach to Identifying Urban Boundaries[J].General Information,2011,43(2):211-227.

[5] 姜世国,周一星.北京城市形态的分形集聚特征及其实践意义[J].地理研究,2006,25(2):204-212.

[6] Batty M,Longley P A.The Morphology of Urban Land Use[J].Environment and Planning B,1988,15(4):461-488.

[7] Feng J,Chen Y.Spatio-temporal Evolution of Urban Form and Land-use Structure in Hangzhou,China:Evidence from Fractals[J].Environment and Planning B,2010,37(5):838-856.

[8] White R,Engelen G.Cellular Automata and Fractal Urban Form:A Cellular Modelling Approach to the Evolution of Urban Land-use Patterns[J].Environment and Planning A,1993,25(8):1175-1199.

[9] White R,Engelen G,Uljee I.The Use of Constrained Cellular Automata for High-resolution Modelling of Urban Land-use Dynamics[J].Environment and Planning B,1997,24(3):323-344.

[10] 卢艳,崔燕平,程淑红.中部地级及以上城市用地扩张的时空演变[J].地域研究与开发,2008,27(4):99-103.

[11] Wang F,Zhou Y.Modelling Urban Population Densities in Beijing 1982—1990:Suburbanisation and Its Causes[J].Urban Studies,1999,36(2):271-287.

[12] 冯健.杭州市人口密度空间分布及其演化的模型研究[J].地理研究,2002,21(5):635-646.

[13] 刘妙龙,陈鹏,冯永玖.上海市人口分形的时空演化与区域差异研究[J].中国人口科学,2005(2):51-60.

[14] 陈彦光.城市人口空间分布函数的理论基础与修正形式——利用最大熵方法推导关于城市人口密度衰减的Clark模型[J].华中师范大学学报:自然科学版,2000,34(4):489-187.

[15] 高向东,郑敏,孙文慧.上海市人口结构空间分布的模型分析[J].中国人口科学,2006(3):61-66.

[16] Frankhauser P.The Fractal Approach,A New Tool for the Spatial Analysis of Urban Agglomerations[J].Population:An English Selection,1998,10(4):205-240.

[17] Batty M.The Size,Scale,and Shape of Cities[J].Science,2008,319:769-771.

[18] Batty M,Longley P A.The Fractal Simulation of Urban Structure[J].Environment and Planning A,1986,18(9):1143-1179.

[19] 余瑞林,王新生,孙艳玲,等.中国城市空间形态分形维及时空演变[J].地域研究与开发,2007,26(2):43-47.

[20] 苏章全,明庆忠,陈英.基于聚集分形维数的旅游区空间结构测评与优化——以云南丽江市古城区为例[J].地域研究与开发,2011,30(5):103-107.

[21] 秦静,方创琳,王洋,等.基于三维计盒法的城市空间形态分维计算和分析[J].地理研究,2015,34(1):85-96.

[22] 王铮,邓悦,宋秀坤,等.上海城市空间结构的复杂性分析[J].地理科学进展,2001,20(4):331-340.

[23] Newling B E.The Spatial Variation of Urban Population Densities[J].Geographical Review,1969,59(2):242-252.

[24] Benguigui L,Marinov M,Czamanski D,etal.When and Where is A City Fractal?[J].Environment and Planning B,2000,27(4):507-519.

[25] 王成栋,凌丹,苗强.分形无标度区的一种自动识别方法[J].计算机工程与应用,2012,48(6):9-12.

[26] 周茂非,倪国锋.首都西南区域经济发展研究[M].北京:中国经济出版社,2008.

[27] 房艳刚,刘鸽,刘继生.城市空间结构的复杂性研究进展[J].地理科学,2005,25(6):754-761.

[28] Waldrop M M.Complexity:The Emerging Science at the Edge of Order and Chaos[M].New York:Simon and Schuster,1993.

[29] 刘安国,杨开忠.克鲁格曼的多中心城市空间自组织模型评析[J].地理科学,2001,21(4):315-322.

Selecting the Dominated Scaling Region for Fractal Urban Center

Huang Weili

(InformationEngineeringInstitute,JiangxiUniversityofTechnology,Nanchang330098,China)

The choice of the origin point for measuring radius dimension is critical in area-radius relationship method. Based on POI(point of interest) data, five types of statistical centers could be computed as candidate origin points. They are geometry center, gravity, density center, geometry center and gravity in midtown. By measuring the number of POIs, scaling region for each center can be detected. Several metrics have been given for estimating the scaling regions, which include the radius of scaling region, the number of POI, central density, radius dimension and drift. The maximization principle of the number of POI is proposed to choose dominated scaling region. It is better than the radius maximization principle in practice. By comparing scaling regions for five centers in Beijing, the scaling region for geometry center has the maximum number of POI. Experiments of major cities in China show the fractal center may be any statistical candidate center or a well-known place, but prefers to the geometry center or density center. Geometry center and gravity in midtown is often valid for some cities with poor symmetry. Most of radius dimensions for these cities are between 1 and 2. Among them, the radius dimension around density center is the minimum. The scaling region, whose radius dimension is less than 1, tends to fall into local density zone. Thus it is possible to avoid local density zone by checking scaling region with a small radius dimension. In addition, nearly 20% of average drift means asymmetrical distribution is common in scaling region. It indicates that the better scaling region could be observed around an alternative center.

dominated scaling region; fractal urban center; area-radius relationship method; point of interest; radius dimension

2015-06-02；

2016-07-20

江西科技学院自然科学基金项目(ZR12YB11,ZR13YB05,ZR14YB10)；协同创新专项课题(XTCX201319)

黄伟力(1980-)，男，江西南昌市人，讲师，硕士，主要从事GIS应用和智能交通研究，(E-mail)huangweili@jxut.edu.cn。

TU984

A

1003-2363(2016)05-0053-07