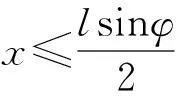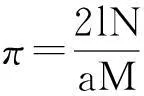蒙特卡罗方法在求解单服务台排队系统中的应用

陈杰东

(广东轻工职业技术学院，广东 广州 510300)



蒙特卡罗方法在求解单服务台排队系统中的应用

陈杰东

(广东轻工职业技术学院，广东 广州 510300)

摘要：随机模拟方法是一种具有独特风格的广义的数值计算方法，同时也是求解实际问题近数值解的一种方法。应用该方法来解决单服务台排队系统的实际问题，具有一定的实用性。

关键词：模拟；模拟方法；蒙特卡罗方法

在实际生活中，我们经常遇到这样的情况：如在一个理发店中，顾客到店中时有理发师正闲着，可随时为顾客服务，有时理发师正处于工作状态，则顾客需要等待，由于顾客到来时间是随机的，我们关心的不是每个顾客各需等待多少时间，而是顾客平均等待时间，这样可以提高理发师的服务效率，我们这里研究的是这类问题中最简单的一种，即单服台排队系统，也就是考虑只有一个服务员的情况。

1背景阐述

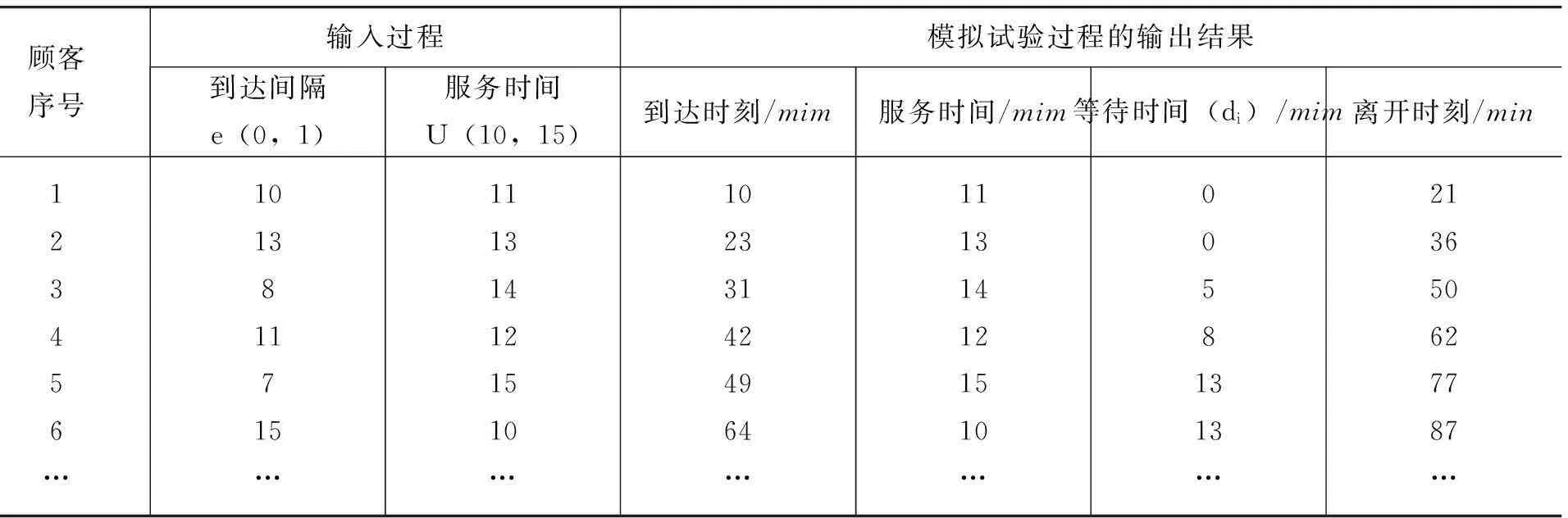
1777年法国学者蒲丰提出用投针试验求圆周率π的问题。给出模型：在平面上画一些间距均为 的平行线，向此平面随机地投掷一枚长针l(l

由于该问题实际操作较麻烦，我们可以用统计模拟试验方法来代替。

(1)产生随机数，首先产生相互独立的随机变量X，φ的抽样序列：{xi,(i=1,……,N)}，其中X～U(0, /2)，φ～U(0,π)。

由此问题可看出，用蒙特卡罗方法求实际问题的基本步骤为：

2随机数的产生

用随机模拟方法解决实际问题时，首先要解决的是随机数的产生方法，或者称随机变量的抽样方法，这里重点介绍[0，1] 区间上均匀分布随机数的产生和检验方法。虽然区间[0，1] 上均匀分布是最简单的连续分布，但产生大量相互独立的U(0，1)随机数对用随机模拟方法解决实际问题是至关重要的；同时很多其他形式的分布(如正态分布，指数分布等)的随机数都可以用U(0，1)随机数经变换得到。下面给出产生区间(a,b)上均匀分布的随机数的具体算法。

若连续型随机变量x的概率密度函数

则称x为(a,b)上均匀分布随机变量，其采样值称为满足均匀分布的随机数，它是这样产生的：首先，由给定的初值x0，按xn+1=5xn产生(0，1)上的均匀分布的随机数ξ；然后，由x=a+ξ(b-a)产生(a,b)上的均匀分布随机数。

过程标识符和形式参数表UDR1(a,b,x0,n) ；a,b区间的左、右端点；x0形成随机数的初值；n所使用机器的二进制尾数的长度。第一次调用本过程时，x0应是小于MN=2↑(n-5)的正奇数，以后再调用时，x0置零。

例如：相继产生(-1，1)区间上的500个和1000个均匀分布随机数，取x0=312657863，计算结果是：

点数N5001000均值Mx=∑Ni=1xi/N-0.00130.0247方差Dx=∑Ni=1(x-Mx)2/N0.34550.3325

3蒙特卡罗方法求解单服务台排队系统

按照莆丰实验的思路，应用蒙特卡罗方法来解决引言所提出的实际问题，这里研究的是这类问题中最简单的一种模型，即单服台排队系统，也就是考虑只有一个服务员的情况，仍以理发师这个例子来看一下此类问题，给出流程：

第一步：收集数据，在实地调查，并收集和处理调查数据，即记录每个顾客到达时刻，等待时间及服务时间等。在这里，可以通过计算机模拟产生随机数来代替这一类过程。

第二步：构造模拟模型。在此模型中，有两个输入的因素：顾客的到达间隔时间和服务时间排队规则是按先到先服务的次序接受服务，服务机构只有一个，即一个服务员每次只能为一个顾客服务。

第三步：模拟试验。我们模拟的模型包含时间因素，即我们要模拟的是服务系统在8小时工作时间内的运行情况，这类模型也称为动态模型。并给出记录模拟时间当前值的变量——模拟时钟及模拟时间的推进原则，推进原则有两种，即下次事件推进原则和均匀间隔(模拟步长)推进原则。

下面就单服务台排队系统的模拟试验，引入几个记号：

记UDR1— 第i个顾客到达时刻(x0=0)

Ti=xi-xi-1：第i-1个顾客至第i个

顾客的到达时间间隔

C4：第i个顾客接受服务的时间

Di：第i个顾客的排队等待时间

Ci=Xi+Si+Di：第i个顾客接受服务后离开的时刻。

顾客到达

排队等待

接受服务

顾客离开

假设服务机构上午8点开门服务(如理发店8点上班)，模拟时钟从T=0开始。产生指数分布e(0,1)随机数，比如得10，13，8，15…。T=10min时，第一个顾客到达，因没有人排队马上接受服务，即 =0min；服务时间s～U(10，15)，产生均匀随机数s，比如得11，13，14，12，…；第一个顾客接受服务时间为11min，计算C1=(10+11+0)min=21min，即第一个顾客于开门后21min离开(即T=21min时离开)。第二个顾客是T=23min=(10+13)min时到达，因第一位顾客已被服务完毕离开了，不必等待，D2=0min，服务时间S1=13min，第二个顾客于C2=(23+13+0)min=36min离开。第三个顾客到达时间X3=31min=(10+13+8)min，时钟T=31min的时候，第二个顾客正在接受服务，故第三位先排队等待时间S3=14min，第三位离开时刻C3=(31+14+5)min=50min；第四位到达时刻X4=(10+13+8+11)min=42min；等待时间D4=(50-42)min=8min，服务时间S4=12min，离开时刻C4=(42+12+8)min=62min；…表中列出模拟试验的部分结果。

表1　单服务员系统的模拟过程

如果改变输入参数，比如提高服务效率，服务员的提高了，服务时间s～U(5，10)，那么等待时间E(D)必然会减少，增加服务人员，同样也可以减少等待时间。

4小结

以上介绍了用随机模拟方法解决单服务台排队系统问题的方法。从解决此类问题的过程中我们可以看到随机模拟方法具有应用面广，适用性强，算法简单等优点，尤其用于处理计算量较大的问题，更可以发挥随机模拟方法的优势。但因为模拟结果具有随机性，且进精度较低，所以在求解精度较高的近似计算中就不宜采用随机模拟方法。

参考文献：

[1]R.Y．Rubinstein.SimulationandtheMonteCarlomethod[M].Wiley，1981.

[2]W.Metropolis,S.Ulam.MonteCarlomethod[M].J.Amer.Statass,1949.

[3]徐仲济.蒙特卡罗方法[M].上海：上海科学出版社,1985.

[4]吴国富.实用数据分析方法[M].北京：中国统计出版社,1992.

[5]徐萃薇.计算方法引论[M].广州：高等教育出版社,1985.

Application of Monte Carlo Method to Solving the Problem of Single-server Queuing System

CHEN Jiedong

(Guangdong Industry Technical College，Guangzhou 510300，China)

Abstract:Stochastic Simulation is a unique style of broad numerical calculation method ,it is also practical problems for nearly a numerical solution method. Using the method to resolve single-server queuing system problems has a certain practicality.

Key words:simulation; analogy method; Monte Carlo method

中图分类号：0026

文献标识码：A

文章编号：1672-1950(2016)01-0009-03

作者简介：陈杰东(1980—)，男，硕士，讲师。

收稿日期：2015-12-18